近年来,气枪震源逐渐用于长炮检距深穿透的深部结构地震探测,为探测深部结构需要采用大容量的气枪或枪阵[1].气枪激发后在水介质中传播,遇到界面后会发生反射、折射、绕射等现象,这些现象对气枪信号都会有改造作用,模拟气枪激发信号的波场传播具有重要意义,能为充分利用气枪震源探测地下结构奠定基础[2].大容量气枪在水中激发产生低频纵波信号,气枪信号传播过程中首先会遇到水介质与水底介质的分界面,研究信号在上覆水层的介质中的传播为充分利用气枪震源奠定基础.
水底介质可能为含有水的多孔介质,因而需要研究双相孔隙介质,1941年Biot建立了孔隙弹性材料的Biot理论[3],1956年,Biot根据流体饱和多孔介质中弹性波的位移特征和吸收特性,建立了弹性波在黏性流体饱和的多孔隙介质中传播的理论[4].该理论假设岩石是均匀各向同性的,充填在岩石骨架中的是可压的黏性流体,孔隙流体相对岩石骨架可自由流,流动过程中二者之间存在摩擦力[5].Biot理论预测了双相介质中第二类纵波(慢纵波)的存在,指出黏滞力控制孔隙流体的相对运动是弹性波在孔介质传播过程中发生衰减的重要机理,从而奠定了双相介质波动理论的基础[6, 7].1980 年,Plona和Berryman分别从实验室观测到慢纵波,证明了 Biot理论的正确性[8].Biot理论主要围绕双相介质之间的耦合机理、耦合程度和耦合结果开展研究,需要研究的问题广泛而复杂,仍是一种正在发展中的波传播理论.
近年来数值模拟地震波传播已成为研究复杂地下结构的有效方法,可以用来探究不同介质构造条件下地震波场传播特性.数值模拟地震波场可以利用数值的方法,重现地震波产生和传播过程中的关键性信息[9].为了对气枪激发产生的纵波源信号在上覆水层的双相孔隙介质中的传播进行模拟,我们研究了地震波数值模拟方法.地震波数值模拟方法主要包括有限差分法、有限元法、伪谱法及谱元法等.有限差分方法是最早被用于地震波传播数值模拟研究中的,它能够有效地实现对横向不均匀性介质地球模型的地震波传播数值模拟,该方法算法简单,计算速度快,占用内存小,但只适应于相对简单的地质模型[10].有限元法适用于空间变化复杂的介质,能够便利地处理自由表面,但低阶有限元法会产生严重数值频散,而高阶有限元法则会出现伪波等问题[11].伪谱法利用快速傅里叶变换对波动方程进行空间求导.它的计算精度高、计算速度快.因为它的空间求导计算是全局性的,要求节点的分布尽量均匀[12].由于谱元法结合了有限元法处理边界结构的灵活性和谱方法的高精度快速收敛等优点,近年来成为地震波数值模拟的重要工具.谱元法最初由Patera 在流体动力学研究中提出[13],Priolo 和 Seriani将其应用于地震波传播的数值模拟[14].Komatitsch 等将谱元法推广到了二维介质中的弹性波数值模拟[15, 16];近年来,Morency 和Jeroen Tromp等开始研究使用谱元法模拟孔隙弹性介质中地震波的传播[17, 18].谱元法的这些最新发展趋势表明该方法是地震波数值模拟的重要工具,在将来的应用中具有巨大的潜力.本文主要研究了利用谱元法模拟水下激发的气枪信号在上覆水层的双相孔隙介质中的波场.
2 谱元法简介谱元法的基本思想是在传统有限元方法的基础上,每一个单元内使用谱方法或者伪谱法,选取正交多项式为基的插值基函数,在各个单元上通过采用高阶插值基函数,提高插值精度,并进而提高数值解的收敛速度.不同的正交多项式展开就可以得到不同形式的谱元法,常见的有Chebyshev谱元法和Legendre谱元法.谱元法运用有限元和伪谱法的思想,在每个单元上进行谱展开,既具有有限元模拟任意复杂介质的韧性,同时又具有伪谱法的精度.Komatitsch等给出了利用谱元法数值模拟地震波传播的理论基础[15, 16].
在网格化过程中,谱元法将模型剖分成多个不重叠的单元,这里我们研究二维情况,所以采用规则或弯曲的四边形.在谱元方法中,为获取高精度的近似解,可以在单元上增加插值点,即增加多项式的阶数来提高精度.在每一个单元上,将定义在节点上的试探函数通过拉格朗日插值得到近似解,任意单元上的函数都可以通过节点上的试探函数的拉格朗日插值得到其近似表达式,介质单元分解后,再进行单元的总体集成,就是把所有单元按照一定的顺序进行组装,得到总方程组,最后通过迭代方法获得结果[19].
本文空间方向上采用Legendre谱元法,在时间域采用显式差分迭代算法求解线性方程组,减少对内存的需求,提高计算效率.为了获得双相介质的波动方程,根据各向同性介质中的广义虎克定律和流体渗透的达西定律,考虑到流体和固体相对运动产生的能量耗散,可以得到双相介质的弹性波方程.首先分析固体和流体中的微观运动方程,然后通过平均化方法获得孔隙介质波传播的宏观描述,为了获得宏观运动方程需做两个关键假设:(1)微观尺度的材料参数是不变的,但在宏观尺度上可变;(2)与平均体积相比波长足够大[20].这样我们可以得到波动方程的积分表达式,也就是弹性波方程的弱积分形式:
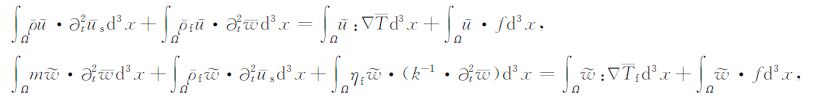
|
其中ρ 是密度,f是体力项,k是渗透率,ηf 是黏滞系数,t为时间,u为位移,w为流体相对固体的位移,T可由各向异性介质的本构理论获得,下标带s的表示固体相的参数,下标带f表示流体相的参数,上面有横线的表示平均化后的参数.
进行数值模拟时,为了实现有限计算区域内真实再现无限区域的波动特征,需要在选取的有限区域外侧设置边界条件,除了地表是自由边界外,其他边界都是人工截断边界.这些人工截断边界会把向外传播的波全部反射回去,从而使正反演工作得不到与实际相符的结果.因此,加入吸收边界条件是数值模拟中必须的.边界条件包括吸收边界条件、衰减边界条件和完全匹配边界条件[21].本文的模拟中主要采取了顶部自由边界条件,其余为吸收边界条件.目前常用的有海绵吸收边界条件和旁轴近似吸收边界条件.海绵吸收边界条件利用黏滞边界或是靠近边界的条带范围内对入射波进行衰减,而旁轴近似边界条件一般对于入射波场和人工边界点的法线夹角较小的情况下精度比较高,本文采用了Clayton和Engquist依据声波方程假定的一个弹性波方程旁轴有理近似的一般形式[22~25].
3 双相介质中波场数值模拟气枪震源激发信号具有丰富的低频有效能量,是一种适合深地壳结构探测的理想低频震源.气枪的子波信号能够通过测量或者数值模拟获得,为简化起见,下面的模拟都采用了Ricker子波,如果要得到气枪激发的结果可以通过反褶积的方法获得.气枪激发产生的纵波信号遇到水底界面时会发生反射和折射,这里我们主要研究水底介质为弹性和双相多孔介质的情况.
3.1 双相多孔介质中的弹性波的传播相对于单相介质理论,双相介质理论能更有效地描述水底介质.水底介质可能为压实沉积物,是一种多孔隙的双相介质,含流体的孔隙各向异性介质由含孔隙或裂隙的固体骨架部分和裂隙中黏弹性不可压缩的流体构成.Biot理论适用于波长远大于孔隙尺寸的情况,它根据干岩石速度估算饱和岩石速度,以及估算速度与频率的关系.孔隙介质中波传播的Biot理论预测了次级胀缩波的存在,这种波衰减很快,为了区分传统的快纵波和剪切波通常叫做“Biot慢纵波".快纵波就是地震勘探中经常观测到的纵波,当液相和固相之间不存在相对运动时,快纵波的振幅具有相同的符号,故称为同相波;慢纵波则是反相波,它实际上是一种扩散波,近似于热传导现象,在离开震源后能量衰减得很快,实际中很难观测到[26].
关于衰减和频散,Biot理论预测当弹性波的趋肤深度与岩石孔隙的直径相近时衰减最大,所谓趋肤深度,是对黏滞性流体在流动时与固体之间的黏滞耦合力随着离开固液分界面的距离而迅速减小现象的一种度量.Biot将弹性波在饱和多孔介质中的传播分为低频和高频范围进行讨论[27].在低频范围内,流体在孔隙中的相对运动为层状黏滞流,趋肤深度大于孔隙直径,黏滞耦合力很大,因此孔隙流体和岩石骨架一起运动,这时波的衰减很小;在高频范围内,层状黏滞流假设不成立,趋肤深度小于孔隙直径,孔隙流体的惯性使其本身的运动落后于骨架的运动,从而造成波的衰减和速度的频散.
为了研究低频波在双相多孔介质中的传播,我们建立了模型,模型尺度4000 m×4000 m, 谱元网格包含300×300个网格,采用规则的四边形网格,时间步长为1.25×10-4s, 总步数为6000,采用P波震源激发,纵波源使用Ricker子波,其主频为30Hz.首先比较有黏滞性和无黏滞性模型中波的传播以研究黏滞性衰减效果.模型1黏滞系数为ηf=0.0001Pa·s, 渗透率为k=10-10m2,模型2 是无黏滞性的.图 1中画出了固体相和流体相中的压力,慢纵波在模型1中快速衰减并表现出扩散行为,满足Biot理论的结果.由图可以知道,在利用纵波源激发的情况下,固相分量中慢纵波几乎很难观察到,在液相分量中同时可以观测到快纵波和慢纵波,且液相分量中慢纵波的振幅较大,证实了Biot双相介质中除了常规的纵波(快纵波)和横波外,还存在第二类纵波(慢纵波)的重要结论,慢纵波的速度明显小于快纵波,而且衰减很快,所以实际中很难观测到.这与杨顶辉在2002年研究中得出的结论一致[11].

|
图 1 (a)固体相中的地震图;(b)流体相中的地震图 实线和虚线分别为黏滞模型和无黏滞模型的结果. Fig. 1 (a) Solid pressure seismograms; (b) Fluid pressure seismograms Solid line for viscous model, dotted line for inviscid model. |
为了研究上覆水层的双相介质中弹性波的反射和透射,我们建立了下面的双层模型,上层为水层,下层为孔隙介质层,模型尺寸4800 m × 4800 m, 源位于(1600,-1700)处,接收仪器位于(1200,-1850)和(1200,-2930)处,顶部是自由边界,其余是吸收边界(采用旁轴近似的一次吸收边界),源采用Ricker子波时间函数,主频为15Hz.模型中取的参数为:水层密度为1000kg/m3,体积模量为2.295GPa, P波速度为1500m/s, S 波速度为零;孔隙介质层固相密度2500kg/m3,液相密度1000kg/m3,孔隙度为0.4,骨架的体积模量和剪切模量分别为10.0GPa和9.63GPa, 液相的体积模量为2.295,黏滞系数为0,孔隙介质中快P波速度为3677m/s, 慢P波速度为1060m/s, S波速度为2378m/s.
图 2给出了分别在水中和在双相介质中的两个接收器得到的SEM 合成地震图.从波场快照上可以看到,直达P波(图 2中a)和反射P波(图 2中b)在水层中的存在,在下部的双相介质层中能够观测到透射P波(图 2中c),P 波到S 波的转换波(图 2中d)以及慢P 波(图 2中e).由于下层属于含有孔隙的双相介质,因此产生了透射慢纵波,而上层为单相介质,所以只有反射纵波和反射横波.

|
图 2 在上覆水层的双相介质里面的波传播模拟:(A)位移垂向分量波场快照;(B)水中和(C)双相介质中接收到的垂向归一化速度分量 Fig. 2 Simulation of wave propagation in a water layer over a homogeneous poroelastic half-space: (A) Snapshot of the vertical-component of displacement; (B)(C)Vertical-component velocity seismograms in water and poroelastic layer |
双相介质中波传播理论由Biot基于实际工作发展而来,描述的是宏观现象,并没有考虑微观水平的过程.依据最近对于平均技术的研究[28],可以基于区域分解从微观尺度的运动方程通过平均化方法得到宏观尺度的方程,从而帮助人们研究描述变孔隙度介质中波的传播.

|
图 3 上覆水层的坚实沉积层中波的传播模拟:(A)波场快照;(B)孔隙度变化;(C)(D)水中和双相介质中接收到的垂向速度分量地震图 Fig. 3 Simulation of wave propagation in a water layer over a compacted sedimentary layer: (A) Snapshot of the vertical- component displacement; (B) Porosity protile in the poroelastic layer; (C)(D) Vertical-component velocity seismograms in water and porosity layer |
我们考虑坚实沉积层水底的情况,假设沉积层中的孔隙度随着深度成指数衰减变化,体积和剪切模量保持不变,这个数值模拟可以解决气枪实验中所遇到的底部界面的选择问题.模型尺寸4800 m×4800m, 源位于(1600,-1700)处,接收仪器位于(1200,-1850)和(1200,-2930)处,顶部是自由边界,其余是吸收边界(采用旁轴近似的一次吸收边界),纵波源采用Ricker子波时间函数,主频为5 Hz.比较这个模型的结果和前面的结果,显示出孔隙度变化的影响.观察在水中的接收结果,两种模型有着相同的到时和幅度;而双相弹性介质中的接收结果则有所不同,这些差异显示出孔隙度变化对于相速度的影响.在孔隙介质下部,孔隙度逐渐减小直至到达弹性界面,孔隙弹性-弹性边界并没表现出较强的反射.
3.4 高速基岩层情况研究水底沉积岩下面为基岩层,基岩与沉积层的波速比、沉积层的厚度是影响气枪激发的波传播的重要因素.气枪激发信号向下传播过程中会遇到高速层覆盖的地区,如玄武岩层,玄武岩是由地幔岩浆喷发至地表而沉积的地层,具有速度高、密度大和层数多等特点,因此玄武岩与沉积岩之间将产生一系列的强波阻抗差界面.强波阻抗界面一方面使得从沉积层中入射到基岩中的波容易被反射回来,另一方面在强速度间断面上也会产生丰富的转换S波.
图 4是针对高阻抗玄武岩厚度变化大的特点而设计的高速粗糙面模型,采用的主频分别是10 Hz和40Hz的Ricker子波.所建立模型尺寸2000m×1600m, 顶部是自由边界,其余是吸收边界(采用旁轴近似的一次吸收边界),纵波源采用Ricker子波时间函数,主频为10Hz和40Hz两种情况.上层为水层,中间层为沉积层,下层为基岩层,气枪在水层激发,接收仪器位于水底,顶部是自由边界,其余是吸收边界(采用旁轴近似的一次吸收边界).水层Vp为1500m/s, 密度1000kg/m3,厚度为100m;第2层为双相介质,双相介质的固体相密度为2500kg/m3,流体相密度为1000kg/m3,孔隙度为20%,固体骨架体积模量为5.34GPa, 流体体积模量为2GPa, 骨架剪切模量为3.2GPa, 厚度为500m;第3层为玄武岩层,纵波速度为4500m/s, 横波速度为2500m/s, 密度为2800kg/m3,厚度为500m;第4层纵波速度为3000m/s, 横波速度为1700m/s, 密度为2500kg/m3,厚度为500m.由两个单炮记录可以看出,受高阻抗层起伏面的影响,不同频率的深层反射信号受浅层绕射波的干扰程度有明显的差异,其中10Hz主频记录中绕射噪声要弱得多,深层反射波组较清晰,资料信噪比较高.说明低频信号受由浅层粗糙表面所产生的绕射波的影响程度较低,因此低频信号具有较强的抗玄武岩起伏面所产生的绕射噪声影响的能力.

|
图 4 波的传播模拟:(a)(b)波场快照;(c)(d)垂直分量的合成地震图 Fig. 4 Simulation of wave propagation in a limited water layer: (a)(b) Snapshot;(c)(d) Vertical-component velocity seismograms |
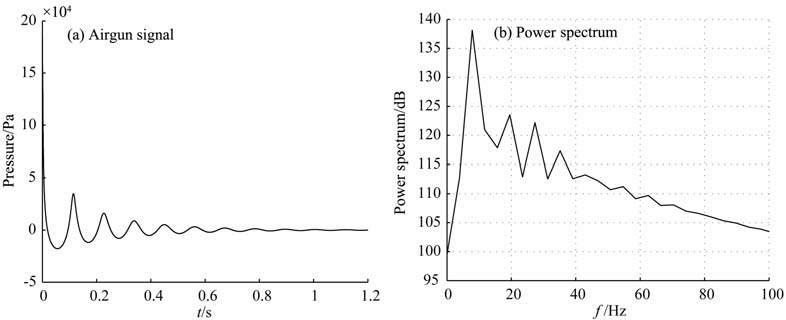
本文研究了起伏水底情况下弹性波场的数值模拟,通过研究波场的特征可以帮助我们了解起伏水底对于波传播的影响效果,从而也能够帮助我们对气枪数据的采集、处理和解释技术加以改进.影响气枪激发能量的主要因素包括气枪容量、充气压力、沉放深度等,如图 5a给出了单枪激发的近场子波模拟信号,单枪的容量为2000in3,充气压力为10MPa, 沉放深度为20m, 气枪近场子波信号包含压力子波和周期性的气泡脉冲子波,图 5b 为气枪子波的功率谱,可以看到气泡脉冲在功率谱上造成的陷波效应.
|
图 5 (a)气枪近场子波信号;(b)功率谱图 Fig. 5 (a)Airgun wavelet signal;(b)Powers pectrum |
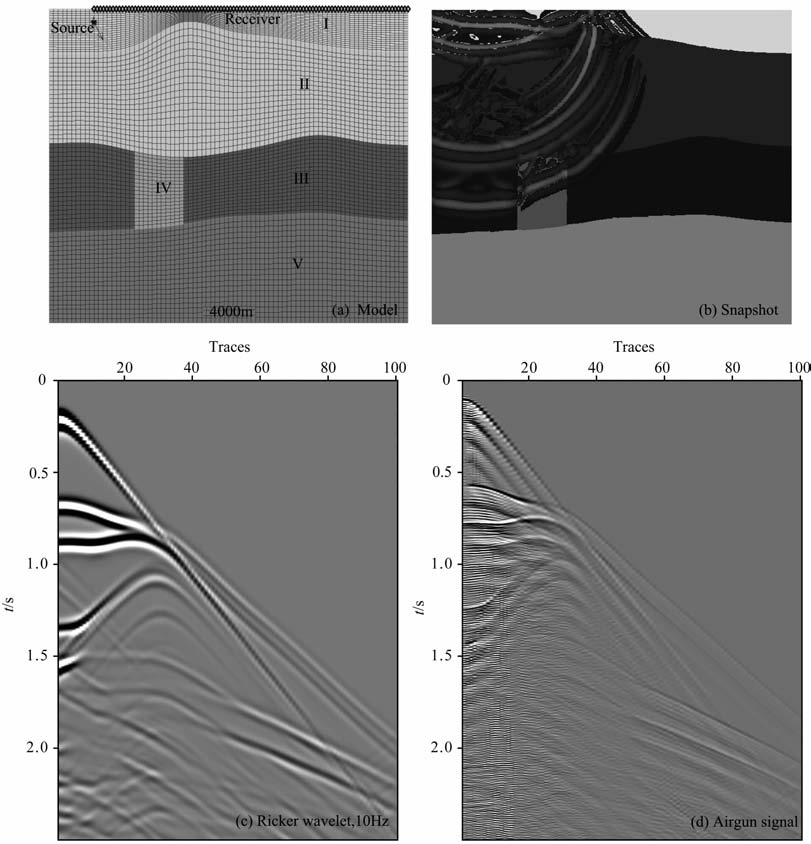
针对起伏界面情况,建立介质模型如图 6所示,模型长度为4000m, 模型厚度为3500m, 包含3个起伏界面,这里我们采用不规则的网格,在不同区域采用了不同的网格密度,这就是可变网格技术,与均匀网格相比,它可以节约大量内存,明显提高计算效率,还能够实现界面的高精度逼近[28].震源信号选取Ricker子波和气枪子波,中心频率为10Hz, 地震信号记录点在水面下10m 处均匀分布.第1层是水层(图 6a中Ⅰ),第2层为双相介质(图 6a中Ⅱ),弹性参数与图 5中第2层相同,第3层(图 6a中Ⅲ)纵波速度为2500m/s, 横波速度为1443 m/s, 密度为2200kg/m3,其中存在低速体(图 6a中Ⅳ)纵波速度2200m/s, 横波速度1343m/s, 密度为2200kg/m3,第4层(图 6a中Ⅴ)纵波速度3000 m/s, 横波速度1732m/s, 密度为2700kg/m3.
|
图 6 (a)模型;(b)波场快照;(c)10 Hz Ricker子波对应的合成地震图;(d)气枪子波信号对应的地震图 Fig. 6 (a)Model; (b)Snapshot; (c) Velocity seismograms for 10 Hz Ricker wavelet;(d) Velocity seismograms for airgun wavelet |
模拟结果如图 6b和图 6c所示,无论在弯曲界面或是水平界面都有明显的反射和透射现象,且波传播过程中,各向异性现象十分明显,图中可以明显地分辨出直达波和反射波等信息.由于气枪源信号包含压力脉冲和气泡脉冲,会影响近源区的接收信号,导致近源区接收到的干扰较多.起伏库底会引起强散射体波和面波以及对地震波传播能量的调制和衰减作用[29],并造成反射波同相轴严重畸变、扭曲,甚至淹没.当然实际水底介质是更为复杂的介质,这需要做进一步的研究.
4 结论及讨论地球内部和地表岩石圈普遍存在着岩石裂缝和裂隙,使得岩石整体上表现为双相各向异性,因而研究这种复杂介质的弹性波场模拟具有十分重要的意义.为了研究水下气枪激发信号的波场,本文利用谱元法对双相孔隙介质中的波场做了数值模拟,分析了地震波的传播特征,验证了双相介质中存在慢纵波的重要结论.通过双相介质中地震波的模拟,表明谱元法对复杂介质模型可以取得很好的模拟效果.本文主要做了以下工作:
(1) 研究了使用SEM 方法模拟孔隙弹性介质中波的传播,使用平均理论实现了从微观到宏观尺度的过渡,研究了孔隙度的变化效果的影响.模拟结果表明,采用谱元法能有效模拟各向异性介质的波场传播.
(2) 双相介质中存在明显的慢纵波,流相波场的慢纵波比固相波场的明显,慢纵波具有很强的散射性质.慢纵波的存在是裂隙液体存在的重要标志,借助慢纵波的出现可以判断孔隙流体的存在,当然目前野外条件尚未获得慢纵波记录,有待于实际工作的努力.
(3) 研究了波在上覆水层的孔隙度变化的沉积层中传播,验证了孔隙度对于相速度的影响.
(4) 借助谱元法分析了高速层存在对于气枪激发信号波场的影响,研究表明低频信号具有较强的穿透高速屏蔽层的能力和较强的抗散射能力.
(5) 研究了起伏界面对波传播的影响,起伏界面会对地震波的传播起到调制和衰减作用.由于气枪源信号包含压力脉冲和气泡脉冲,会导致近源区接收到的干扰较多.
| [1] | Tang J, Wang B S, Ge H K, et al. Experiment and simulation of large capacity air-guns in deep structure exploration. Earthquake Research in China , 2009, 23(4): 1-11. |
| [2] | Chen Y, Liu L B, Ge H K, et al. Using an airgun array in a land reservoir as the seismic source for seismotectonic studies in northern China: experiments and preliminary results. Geophysical Prospecting , 2007, 56(4): 601-612. |
| [3] | Biot M A. General theory of three-dimensional consolidation. J. Appl. Phys. , 1941, 12(2): 155-164. DOI:10.1063/1.1712886 |
| [4] | Biot M A. Theory of propagation of elastic waves in a fluid saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am. , 1956a, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [5] | Biot M A. Theory of propagation of elastic waves in a fluid saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. , 1956b, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [6] | Biot M A. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. , 1962a, 33(4): 1482-1498. DOI:10.1063/1.1728759 |
| [7] | Biot M A. Generalized theory of acoustic propagation in porous dissipative media. J. Acoust. Soc. Am. , 1962b, 34(9A): 1254-1264. DOI:10.1121/1.1918315 |
| [8] | Plona T J. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Appl. Phys. Lett. , 1980, 36(4): 259-261. DOI:10.1063/1.91445 |
| [9] | 邵秀民, 蓝志凌. 非均匀各向同性弹性介质中地震波传播的数值模拟. 地球物理学报 , 1995, 38(Suppl.): 39–55. Shao X M, Lan Z L. Numerical simulation of the seismic wave propagation in homogeneous isotropic elastic media. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1995, 38(Suppl.): 39-55. |
| [10] | 刘恩儒, 岳建华, 刘彦. 具有离散裂缝空间分布的二维固体中地震波传播的有限差分模拟. 地球物理学报 , 2006, 49(1): 180–188. Liu E R, Yue J H, Liu Y. Finite difference simulation of seismic wave propagation in 2-D solids with spatial distribution of discrete fractures. Chinese J. Geophys. (in Chinese) , 2006, 49(1): 180-188. |
| [11] | 杨顶辉. 双相各向异性介质中弹性波方程的有限元解法及波场模拟. 地球物理学报 , 2002, 45(4): 575–583. Yang D H. Finite element method of the elastic wave equation and wavefield simulation in two-phase anisotropic media. Chinese J. Geophys. (in Chinese) , 2002, 45(4): 575-583. |
| [12] | Orszag S A. Spectral methods for problems in complex geometries. J. Comput. Phys. , 1980, 37(1): 70-92. DOI:10.1016/0021-9991(80)90005-4 |
| [13] | Patera A T. A spectral element method for fluid dynamics: laminar flow in a channel expansion. J. Comput. Acoust. , 1984, 54(3): 468-488. |
| [14] | Priolo E, Seriani G. A numerical investigation of Chebyshev spectral element method for acoustic wave propagation. Proceedings of the 13th IMACS Conference on Comparative Applied Mathematics. Dublin, Ireland, 1991. 551~556 |
| [15] | Komatitsch D, Tromp J. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. , 1999, 139: 806-822. DOI:10.1046/j.1365-246x.1999.00967.x |
| [16] | Komatitsch D, Vilotte J P. The spectral-element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures. Bull. Seism. Soc. Am. , 1998, 88(2): 368-392. |
| [17] | Morency C, Luo Y, Tromp J. Finite-frequency kernels for wave propagation in porous media based upon adjoint methods. Geophys. J. Int. , 2009, 179(2): 1148-1168. DOI:10.1111/gji.2009.179.issue-2 |
| [18] | Tromp J, Komatitsch D, Liu Q Y. Spectral-element and adjoint methods in seismology. Comm. in Comput. Phys. , 2008, 3(1): 1-32. |
| [19] | Luo Y, Zhu H J, Nissen-Meyer T, et al. Seismic modeling and imaging based upon spectral-element and adjoint methods. The Leading Edge , 2009, 28(5): 568. DOI:10.1190/1.3124932 |
| [20] | Morency C, Tromp J. Spectral-element simulations of wave propagation in poroelastic media. Geophys. J. Int. , 2008, 175: 301-345. DOI:10.1111/gji.2008.175.issue-1 |
| [21] | Zeng Y Q, Liu Q H. Acoustic detection of buried object in 3-D fluid saturated porous media: numerical modeling. IEEE Trans. Geosci. Remote Sens. , 2001, 39(6): 1165-1173. DOI:10.1109/36.927434 |
| [22] | Clayto R, Engquist B. Absorbing boundary conditions for acoustic and elastic wave equations. Bull. Seism. Soc. Am. , 1977, 67(6): 1529-1540. |
| [23] | Higdon R L. Absorbing boundary conditions for acoustic and elastic waves in stratified media. J. Comput. Phys. , 1992, 101(2): 386-418. DOI:10.1016/0021-9991(92)90016-R |
| [24] | Yang D H, Wang S Q, Zhang Z J, et al. n-times absorbing boundary conditions for compact finite-difference modeling of acoustic and elastic wave propagation in the 2-D TI Medium. Bull. Seism. Soc.Am. , 2003, 93(6): 2389-2401. DOI:10.1785/0120020224 |
| [25] | Wang X M, Tang S Q. Analysis of multi-transmitting formula for absorbing boundary conditions. International Journal for Multicsale Computational Engineering , 2010, 8(2): 207-219. DOI:10.1615/IntJMultCompEng.v8.i2 |
| [26] | Arntsen B, Carcione J M. Numerical simulation of the Biot slow wave in water-saturated Nivelsteiner sandstone. Geophysics , 2001, 66(3): 890-896. DOI:10.1190/1.1444978 |
| [27] | Bear J. Dynamics of Fluids in Porous Media. New York: American Elsevier Publishing Company Inc., . |
| [28] | de Basabe J D, Sen M K. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations. Geophysics , 2007, 72(6): T81-T95. DOI:10.1190/1.2785046 |
| [29] | 王童奎, 李瑞华, 李小凡, 等. 横向各向同性介质中地震波场谱元法数值模拟. 地球物理学进展 , 2007, 22(3): 778–784. Wang T K, Li R H, Li X F, et al. Numerical spectral-element modeling for seismic wave propagation in transversely isotropic medium. Progress in Geophysics (in Chinese) , 2007, 22(3): 778-784. |
 2011, Vol. 54
2011, Vol. 54

