2. 成都理工大学数学地质四川省高校重点实验室,成都 610059;
3. 牛津大学应用数学计算中心,牛津;
4. 成都理工大学油气藏地质及开发工程国家重点实验室,地球探测与信息技术教育部重点实验室,成都 610059
2. Key Lab of Geomathematics of Sichuan Province, Chengdu University of Technology, Chengdu 610059, China;
3. Oxford Centre for Collaborative Applied Mathematics, Oxford, UK;
4. State Laboratory of Oil/Gas Reservoir Geology and Exploitation, Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu 610059, China
地球物理反演在地球物理数据处理中占有重要的地位,电磁波电导率反演层析成像是一种地球物理探查手段,在工程技术、环境地质调查以及矿产资源勘探等领域有着广泛的使用价值.文献[1]详细讨论了电磁波电导率反演成像方程的建立问题.电导率反演成像方程一般都是规模巨大的不适定方程,算法选择或设计的难点在于巨型高度不适定矩阵算子方程的准确解算与海量计算的实现.不同的解算方法得到的结果可能会有较大的差别,因此改进算法,提高该方法求解结果的精确性,这将进一步促进该方法的实际应用,提高其实用价值[2].
随着计算技术的进步,有关反演算法的应用研究受到人们越来越多的关注,正则化方法在模型参数反演中也获得了广泛的应用[3~8].文献[2, 9]对电导率反演成像方程的求解算法方面进行了较深入的探讨.其中文献[9]针对电导率非负的特性,引入正则化参数,将问题转化为一个非负最小二乘问题,并用active-set算法求解.取得了较满意的结果.文献[2]又提出了一种新的基于LSQR 算法的混合差分进化算法进行求解.本文将进一步研究正则化的电导率反演成像的计算方法,提出了正则化的电导率反演计算的双参数混合型反演方法.并结合与截断奇异值分解法,正则化的共轭梯度法及Tikhonov正则化方法的比较,通过理论模型的模拟对比,验证了该方法的优越性,对实际测量数据的数值计算表明了该方法的有效性.
2 正则化方法与正则参数的选取电导率反演层析成像通常可以写成矩阵表达的形式[9]:
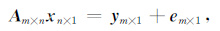
|
(1) |
其中,系数矩阵A为贡献度矩阵,x为未知的电导率参数,y为由观测数据得到的已知向量,e为误差向量,包含测量误差和在近似计算过程中产生的误差.为得到电导率参数x,可采用Tikhonov正则化方法求解.
给定参数α>0,选择xα∈X使得
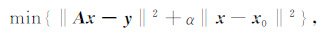
|
(2) |
其中α为Tikhonov正则化参数,x0 为电导率参数x的一个先验值,(2)式的极小解xα ∈ X是连续依赖于参数α >0的.在实施正则化方法过程中,确定合适的正则化参数是核心问题之一[10~16],参数的选取应使得观测数据的误差与实施正则化过程产生的误差相一致.考虑Tikhonov 正则解xα = (αI+A*A)-1A*y,α >0.应用A的奇异系统,它可以表示为[17]:
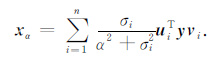
|
(3) |
L-曲线准则是指以log -log 尺度来描述‖xα‖2 与‖Axα-y‖2 的曲线对比,进而根据该对比结果来确定正则化参数的方法.L曲线中垂直部分相应的正则化解的范数‖xα‖2 对α 的选取非常敏感,而水平部分对应的正则化解的残差‖Axα -y‖2 对α 的选取也非常敏感.所以为了平衡这两个量,必须选取参数α 对应于L曲线中垂直部分和水平部分的交点.具体如下:对于连续的正则化参数α,计算曲线
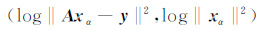
|
的曲率,找到其曲率极大点,也就是L曲线的拐点,确定最佳正则化参数[18].
2.2 Morozov的偏差原理[19]设原始数据的精度是δ,存在这样的正则化参数α(δ),使其满足偏差方程:
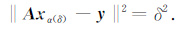
|
(4) |
令

|
其中,A(α)=A(A*A+αI)-1A* ,tr(I-A(α))=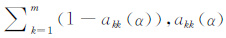
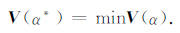
|
(5) |
此法源于统计估计理论中选择最佳模型的 PRESS准则,但比它更为稳健[11, 17].
3 双参数混合正则化方法文献[20]讨论了基于双参数正则化的非线性不适定问题,并研究证明了关于此问题解的存在性,稳定性和收敛性.文献[21]中为求解线性不适定问题的稳定的数值近似解引入了带双参数的混合正则化方法理论.
为求得方程(1)的一个更加稳定的近似解,并且减少多解性,我们基于标准形式的Tikhonov 正则化方法,通过引入带有二阶正则算子的正则化项,建立了带双参数的正则化方法,即下述极小化问题
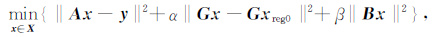
|
(6) |
的一个解作为方程(1)的近似解.第一个正则化项‖Gx-Gxreg0‖2 可以看作是引入了对电导率参数x的约束,xreg0 是电导率参数的先验值,它是由前述的截断奇异值分解法、共轭梯度法及标准Tikhonov正则化法分别求解后再进行联合优化所确定,具体来说,就是根据前述三种方法的解分别乘以权重再求和来确定(例如权重可依次取为0.3,0.3,0.4),先验值的有效确定可显著提高求解效率,G为离散化后与正则算子相对应的正则矩阵,在此选取为二阶正则矩阵,它表示为
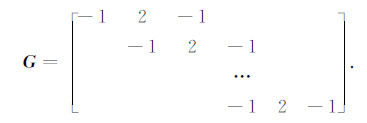
|
第二个正则化项是在‖Bx‖2 中选取B为单位阵,即B=I,此时,该项可简化为‖x‖2.这里α >0,β >0分别为正则化参数.这里的正则化参数的值分别由前述的L-曲线准则,Morozov的偏差原理及广义交叉校验准则分别进行计算[10],在得到各种方法下的最优正则化参数以后,对这些参数再进行优化组合,以此得到最佳正则化参数.求解极小化问题(6)式,可以首先确定正则化参数α,然后再确定正则化化参数β,因而完全类似于求解标准的Tikhonov正则化问题.
4 数值反演结果 4.1 理论模型反演测试为了验证本文提出的双参数混合正则化方法的优越性,我们进行理论模型试验.以Hilbert矩阵作为系数阵的矩阵方程
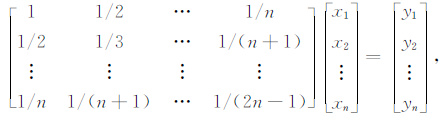
|
(7) |
在n较大的时候为病态矩阵.我们在(7)式中选择了n=101,这时其条件数高达2.05×1019.在试验中,我们对右端项y加入噪声,假定该噪声具有可加性,则

|
(8) |
其中,δ 为噪声水平,rand(size(ytrue))具有与ytrue维数一致的Gauss噪声,噪声水平在试验中分别取为0,0.1和0.3.我们通过前述的截断奇异值分解法、共轭梯度法、标准Tikhonov 正则化法和双参数混合正则化方法分别进行反演计算,计算结果分别如图 1~4所示.与截断奇异值分解法,共轭梯度法和标准Tikhonov正则化法相比较,反演测试结果表明双参数混合正则化方法不仅具有较高的反演计算精度,而且对于数据的随机噪声是稳定的.

|
图 1 噪声水平为0(a),0.1(b)和0.3(c)时的真实解(虚线) 和截断奇异值分解法的解(实线) Fig. 1 Comparison between actual solution (dotted line) and TSVD solution (solid line) |
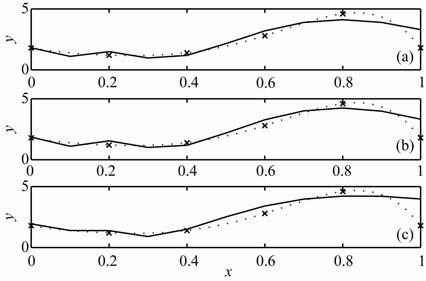
|
图 2 噪声水平为0(a),0.1(b)和0.3(c)时的真实解(虚线) 和共轭梯度法的解(实线) Fig. 2 Comparison between actual solution (dotted line) and CG solution (solid line) |
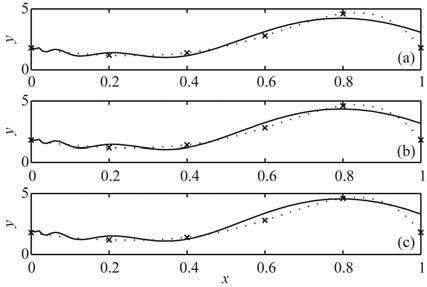
|
图 3 噪声水平为0(a),0.1(b)和0.3(c)时的真实解(虚线) 和标准Tikhonov正则化解(实线) Fig. 3 Comparison between actual solution (dotted line) and Tikhonov regularization solution (solid line) |
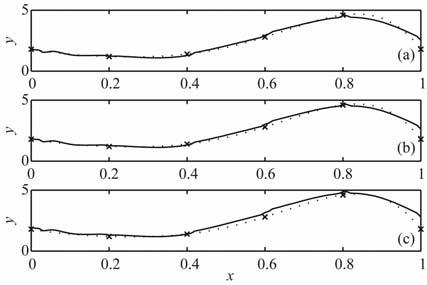
|
图 4 噪声水平为0(a),0.1(b)和0.3(c)时的真实解(虚线) 和双参数混合正则化解(实线) Fig. 4 Comparison between actual solution (dotted line) and dual-parameter regularization solution (solid line) |
下面仍然以文献[1]中所述的背景资料为例,通过电导率成像反演实际应用模拟,对上述算法进行验证分析.为调查某一大型建筑的地基,进行了数对井间剖面的电磁成像测量.所用仪器为国产J-W4型井中电磁波仪.采用定点发射,有限扇区扫描观测方式采集数据.发射点距1 m, 接受点距0.5 m, 并在各剖面进行了激发接收互换观测.在每一观测点以2MHz为间隔,扫描记录了从12MHz到32 MHz的11个频率的数据.现有观测数据882 个,未知电导率参数个数为22×55=1100个.在这里,测试方程的系数矩阵A为882×1100型的,其秩为748,条件数为1.65×1031,这是一个高度病态矩阵.
我们通过前述的截断奇异值分解法、共轭梯度法、标准Tikhonov 正则化法和双参数混合正则化方法分别进行反演计算地层电导率.反演结果分别如图 5~8所示.与上述几种正则化方法相比较,成像结果表明用本文双参数混合正则化方法得到了精确细致可靠的电导率成像图.成像图所反映的电性结构特征与钻探所揭露的剖面地质特征是基本一致的,连续性也较好,与钻探资料和地质规律吻合.
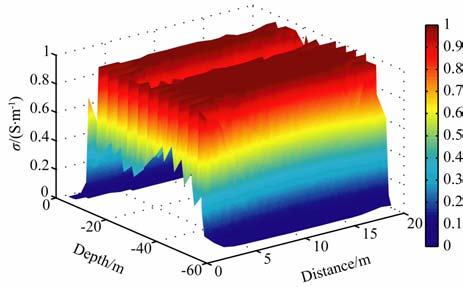
|
图 5 截断奇异值分解法反演的电导率成像图 Fig. 5 Conductivity tomogram by TSVD |
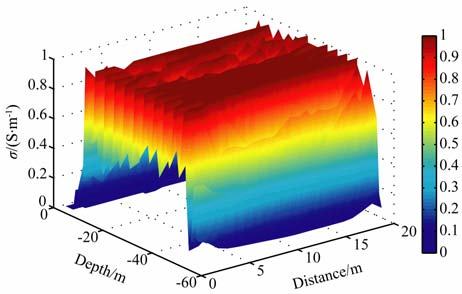
|
图 6 共轭梯度法反演的电导率成像图 Fig. 6 Conductivity tomogram by CG |

|
图 7 标准Tikhonov正则化反演的电导率成像图 Fig. 7 Conductivity tomogram by Tikhonov regularization |

|
图 8 双参数混合正则化反演的电导率成像图 Fig. 8 Conductivity tomogram by dual-parameter regularization |
(1) 本文讨论的双参数混合正则化方法是一种反演计算电导率参数的有效算法.数值反演结果表明,在同一成像方程,同一观测数据的条件下,通过与截断奇异值分解法、共轭梯度法、标准Tikhonov正则化法相比较,本文建立的正则化方法是更加有效的,对于数据的随机扰动也有较好的稳定性,得到的电导率反演成像更加精确细致可靠,也符合实际情况.
(2) 正则化方法是解决不适定问题的有效方法,其中正则化项可以看作是包含了问题的先验信息,它的引入可以改善问题的病态性,而通过选取不同的正则矩阵可以改变正则化项所包含的先验信息,本文通过引入带有二阶正则矩阵的正则化项提高了电导率反演成像的精确度.
(3) 在实施正则化方法过程中,正则化参数的选取是至关重要的,本文通过L曲线准则,Morozov的偏差原理及广义交叉校验准则的联合计算得到最佳正则化参数,虽然获得了更加稳定的反演结果.但由于增加了计算工作量,所以该方法在本文的中小规模问题是适用的,对于大规模问题还需要研究更加强适的算法.
(4) 本文所述的双参数正则化方法与其他计算方法相比较,可以获得效率更高的反演结果.比如文献[22]所述方法求解所花费时间为346.86s, 而本文所述方法求解仅需66.56s.
| [1] | Cao J X, He Z H, Zhu J S, et al. Conductivity tomography at two frequencies. Geophysics , 2003, 68(2): 516-522. DOI:10.1190/1.1567219 |
| [2] | 潘克家, 王文娟, 谭永基, 等. 基于混合差分进化算法的地球物理线性反演. 地球物理学报 , 2009, 52(12): 3083–3090. Pan K J, Wang W J, Tan Y J, et al. Geophysical linear inversion based on hybrid differential evolution algorithm. Chinese J. Geophys. (in Chinese) , 2009, 52(12): 3083-3090. |
| [3] | 肖庭延, 于慎根, 王彦飞. 反问题的数值解法. 北京: 科学出版社, 2003 . Xiao T Y, Yu S G, Wang Y F. Numerical Methods for the Solution of Inverse Problems (in Chinese). Beijing: Science Press, 2003 . |
| [4] | 顾勇为, 归庆明, 边少锋, 等. 地球物理反问题中两种正则化方法的比较. 武汉大学学报 , 2005, 30(3): 238–241. Gu Y W, Gui Q M, Bian S F, et al. Comparison between Tikhonov regularization and truncated SVD in geophysics. Chinese J. of Wuhan University (in Chinese) , 2005, 30(3): 238-241. |
| [5] | 李功胜, 姚德, 马昱, 等. 一维溶质运移源(汇)项系数反演的迭代正则化算法. 地球物理学报 , 2008, 51(2): 582–588. Li G S, Yao D, Ma Y, et al. An iterative regularization algorithm for determining source (sink) coefficient in 1-D solute transportation. Chinese J. Geophys. (in Chinese) , 2008, 51(2): 582-588. |
| [6] | 王彦飞, 杨长春, 段秋梁. 地震偏移反演成像的迭代正则化方法研究. 地球物理学报 , 2009, 52(6): 1615–1624. Wang Y F, Yang C C, Duan Q L. On iterative regularization methods for migration deconvolution and inversion in seismic imaging. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1615-1624. |
| [7] | 刘海飞, 阮百尧, 柳建新, 等. 混合范数下的最优化反演方法. 地球物理学报 , 2007, 50(6): 1877–1883. Liu H F, Ruan B Y, Liu J X, et al. Optimized inversion method based on mixed norm. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1877-1883. |
| [8] | 闫永利, 陈本池, 赵永贵, 等. 电阻率层析成像非线性反演. 地球物理学报 , 2009, 52(3): 758–764. Yan Y L, Chen B C, Zhao Y G, et al. Nonlinear inversion for electrical resistivity tomography. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 758-764. |
| [9] | 王文娟, 潘克家, 曹俊兴, 等. 基于Tikhonov正则化的双频电磁波电导率成像反演. 地球物理学报 , 2009, 52(3): 750–757. Wang W J, Pan K J, Cao J X, et al. Electrical conductivity imaging using dual-frequency EM data based on Tikhonov regularization. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 750-757. |
| [10] | Kilmer M E, Hansen P C, Espanol M I. A Projection-based Approach to General-form Tikhonov regularization. SIAM J. Sci. Comput. , 2007, 29(1): 315-330. DOI:10.1137/050645592 |
| [11] | Golub G H, Hansen P C, O'leary D P. Tikhonov regularization and total least squares. SIAM J. Matrix Anal. , 1999, 21(1): 185-194. DOI:10.1137/S0895479897326432 |
| [12] | Hansen P C, Jensen T K, Rodriguez G. An adaptive pruning algorithm for the discrete L-curve criterion. Journal of Computational and Applied Mathematics , 2007, 198(2): 483-492. DOI:10.1016/j.cam.2005.09.026 |
| [13] | Hansen P C, Kilmer M E, Kjeldsen R H. Exploiting residual information in the parameter choice for discrete Ill-posed problems. BIT Numerical Mathematics , 2006, 46(1): 41-59. DOI:10.1007/s10543-006-0042-7 |
| [14] | Jacobsen M, Hansen P C, Saunders M A. Subspace preconditioned LSQR for discrete ill-posed problems. BIT Numerical Mathematics , 2003, 43(5): 975-989. DOI:10.1023/B:BITN.0000014547.88978.05 |
| [15] | Hansen P C, Jensen T K. Smoothing-Norm preconditioning for regularizing minimum-residual methods. SIAM J. Matrix Anal. , 2006, 29(1): 1-14. |
| [16] | Jensen T K, Hansen P C. Iterative regularization with minimum-residual methods. BIT Numerical Mathematics , 2007, 47(1): 103-120. DOI:10.1007/s10543-006-0109-5 |
| [17] | 王彦飞. 反演问题的计算方法及其应用. 北京: 高等教育出版社, 2007 . Wang Y F. Computational Methods for Inverse Problems and Their Applications (in Chinese). Beijing: Higher Education Press, 2007 . |
| [18] | Hansen P C, O'Leary D P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. , 1993, 14(6): 1487-1503. DOI:10.1137/0914086 |
| [19] | Morozov V A. Methods for Solving Incorrectly Posed Problems. New York: Springer-Verlag, 1984 . |
| [20] | 杨宏奇, 侯宗义. 非线性不适定算子方程的双参数正则化方法. 数学物理学报 , 2004, 24A(2): 129–134. Yang H Q, Hou Z Y. Two-parameter regularization method for nonlinear ill-posed operator equations. Acta Mathematica Scientia (in Chinese) , 2004, 24A(2): 129-134. |
| [21] | Dombrowsky T P. An Introduction to Aspects of Industrial and Environmental Inversion Problems. Oxford: Oriel College, University of Oxford, 2005 . |
| [22] | Wang W J, Pan K J, Cao J X. Conductivity Tomography Imaging using Regularization Methods. Journal of Information and Computation Science , 2008, 5(4): 1885-1891. |
 2011, Vol. 54
2011, Vol. 54


