山体表面重构主要是通过对山体内部热传导规律和山体表面运动规律这样一个耦合模型进行研究,得到数百万年以前山体表面分布情况,从而得到该区域地形地貌的变化规律.山体表面重构问题在国外已经引起了越来越多的地质学家和数学家的关注,已有大量的文献报道和实际山体数据的处理结果[1~6].
山体表面重构在很多实际问题中有重要的应用价值,例如在石油勘探,地质动力学,地质结构学等领域均有应用.从地质学角度讲,山体表面重构是山体内部热传导模型(Heat transfer process model, HTPM)和山体表面运动模型(Surface process model, SPM)这两个过程相互作用的结果;从数学角度讲,这是一个三维热对流扩散方程和一个二维热对流扩散方程的耦合方程组.前者是针对扩散项反演,而后者则是针对初始值进行反演.很多学者分别针对这两个方程进行研究[2, 5, 7, 8],这些研究说明了数学模型的合理性.在实际应用中,测量数据主要是以下两类:第一类,通过对山体内岩石中的同位素[2, 5, 6, 7, 9~12]的测量,经过温度和同位素半衰期的关系,计算出岩石的历史温度,将这些历史温度作为三维热对流扩散方程测量数据;第二类,将山体表面的当前分布情况作为二维热对流扩散方程测量数据[8].迄今为止,还没有文献将这两个方程作为一个耦合系统进行研究.本文主要针对该耦合方程提出有效的山体表面重构算法,并从数值模拟的角度给出算法的实现过程和重构效果.
山体表面重构存在本质上的困难:在计算的规模上,无论是空间和时间上都是大尺度;在计算的非线性程度上,由于测量数据的有限性,使得该问题是一个高度非线性的反演问题.在计算过程中,为了解决这些困难,我们采用同伦延拓方法求解三维热对流扩散方程,至于二维热对流扩散方程并不应用这样的算法,这主要是因为,从计算复杂度和测量数据的角度讲,前者复杂度远远大于后者,这样就造成前者罚函数的极值随着网格剖分的加细而迅速增多,这样就对初值的选取有很高的要求,如果初值选取不当,就会计算到离初值最近的极小点,无法计算到最终要求的最小值.而同伦延拓算法恰恰能够弥补这样的不足,并且已经在一些复杂问题上得到了很好的应用,例如:在弹性固体介质[13]、黏弹性固体介质[14]、弹性双相介质[15, 16]和黏弹性双相介质[13]中都取得了较好的应用效果,克服了常规迭代法对初值强烈依赖的缺点,具有收敛速度快、收敛范围大的优点,非常适用于求解初值难以获取的高度非线性反演问题.本文将采用该方法对山体表面进行重构.
考虑到测量数据存在误差和不充分性,还有问题本身的非线性性质,将山体表面重构过程归结为对罚函数(一类非线性泛函)的优化问题.实验表明,同伦延拓算法对于这样的问题除了克服了初值依赖性,还具有较好的稳定性.由于该问题没有解析解,因此利用有限元来求解该问题,给出具体的离散格式,为了有效地求得罚函数的导数,本文也给出了利用对偶法求导数的过程.通过数值算例说明,同伦延拓算法针对这一问题具有很好的收敛性和较好的稳定性.
2 数学模型山体表面重构的数学模型主要包括HTPM 和SPM.
2.1 HTPM 数学模型HTPM 数学模型主要描述山体内部的热传导情况,包括以下三个方面:热对流(heat conduction)、岩石移动引起的热扩散(transportation of rocks)还有放射性元素的辐射能量(finite concentration of radioactive isotopes).假设考虑的模型定义在下面区域内:
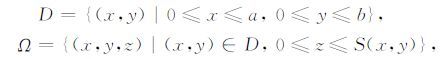
|
这里S(x,y)表示山体表面分布情况.HTPM 满足下面的三维对流扩散方程[3]:
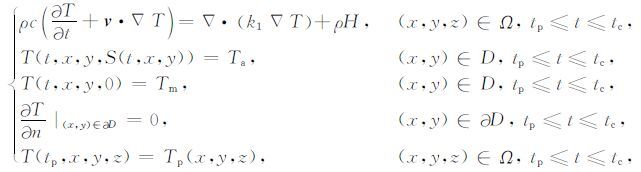
|
(1) |
这里ρ 为介质密度,c为热容,k1 为热传导系数,H为单位质量介质中放射性元素辐射热量.Ta 表示山体表面温度,一般认为是空气温度,Tm 表示山体下边界的温度,一般认为是岩石的融化温度,Tp 表示初始温度.以上这些量在实际问题中都是已知的.v= (v1,v2,v3)表示岩石移动速度,是待反演参数.S是山体表面,这个量由下面SPM 模型决定.
2.2 SPM 数学模型SPM 数学模型主要描述山体表面演变过程,包括以下三个方面:山坡运动对山体表面的影响(hillslo peprocess)、山体表面的水平运动和垂直运动影响(transport and uplift)和河流冲刷因素(fluvial process).将这三个因素考虑后得到下面的SPM 方程描述山体表面运动过程[8]:

|
(2) |
这里k2 为山坡扩散速度,a为比例常数,Q,d分别表示河流冲刷能力和河流流经方向,u= (v1,v2),u3 =v3 分别表示在山体表面的速度水平分量和垂直分量,这些都是已知量.S(x,y),Sp(x,y)分别表示山体表面在(x,y)点处的高度和初始值.
3 山体表面重构耦合系统反问题山体表面重构问题实际是由方程(1)和(2)组成的耦合系统反演问题.这两个方程通过下面的形式进行耦合:方程(1)中移动边界S(t,x,y)是方程(2)的解,方程(2)中的山体表面速度水平分量和垂直分量是u,而u3又来自于方程(1)中的岩石运动的速度v.
3.1 测量数据测量数据作为反演问题的重要组成部分,直接影响到反演算法的构造和算法的可靠性.在本文中,测量数据分为两大类:一类是方程(1)中的测量数据,在实际应用中利用对放射性同位素的测量得到岩石的历史温度,记为:Z(tn,xj(tn))= T(tn,xj(tn)),j=1,2,…,m;n=0,2,…,N,tp ≤t1 <t2< …<tl-1 <tl≤tc;另一类是方程(2)中的测量数据,在实际应用中就是针对山体表面现在时刻的分布情况的测量,记为:S(tc, x,y).
值得注意的是测量数据Z(t,xj(t))的位置是随着时间变化的,并不是固定的,为了简化,在本文中假设位置的移动仅仅是速度的函数:

|
最终目的是利用这两类测量数据进行反演计算得到最初的山体表面分布情况S(tp, x,y),从而利用方程(2)就可以计算出任意时刻的山体表面分布情况S(t,x,y),tp<t<tc.
3.2 数值算法 3.2.1 假设由于方程(1)是一个移动边界问题,它的上边界S(t,x,y),tp<t<tc由方程(2)决定,为了解决这样
一个计算难题,给出下面符合实际的假设:

|
这里tp =t0<t1 < … <tN=tc 是[tp,tc] 的一个物理剖分,并不是数值计算的数值剖分.
在本算例中第一类测量数据为:

|
山体表面也做类似假设:
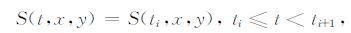
|
这样就将移动边界问题转化为若干个固定边界问题,更加易于处理.
3.2.2 算法(1) 给出速度初值vk(ti,x),i=0,1,…,N-1和山体表面在时刻tp 初值Sk(tp, x,y),x∈ D,这里指标k表示迭代次数;
(2) 当S(tp, x,y)固定,利用第一类测量数据Z(t,xj(t)),j=1,2,…,m,对速度v(ti,x),i=0,1,…,N-1进行迭代;
(3) 当v(ti,x),i=0,1,…,N-1固定,利用第二类测量数据S(tc, x,y),对初始值S(tp, x,y)进行迭代.
将前面的步骤进行循环,直到满足一定的停止准则为止,事实上,第二步和第三步对速度场和山体表面的初始值进行迭代校正.第二步和第三步的算法细节部分将在下面给出.为了迭代S(tp, x,y)和v(t,x),采用梯度法优化罚函数,在对罚函数求导的时候,利用对偶方程既减少了计算量又提高了准确性.
3.3 当S(tp, x,y)固定,迭代速度场v(t,x)(1) 利用已给的vk(ti,x),i= 0,1,…,N-1,可以得到u(ti,x),u3(ti,x),i=0,1,…,N-1,再将已给的Sk(tp, x,y)代入SPM 中,通过正演计算可以得到
Si(t,x,y)=S(ti,x,y),(x,y)∈D,i=0,1,…,N.
(2) 在t0<t<t1 区间内求解HTPM,速度为给定的vk(t0,x).在时刻t0 的温度T0 =Tp 是已知的,计算得到时刻t1 的温度场表示为T1,它作为下一个时间段t1 <t<t2 温度场的初始值.
(3) 利用测量数据Z(t,xj(t)),j=1,2,…,m,t0 ≤t≤t1 对vk(t0,x)进行迭代,本文中主要是利用同伦延拓方法进行迭代,不仅具有较好的稳定性还具有大范围收敛的作用.
(4) 在ti<t<ti+1,i=1,2,…,N-1区间内重复第二步和第三步.
为了对速度场v(t,x)进行迭代,定义如下的同伦延拓法罚函数:

|
(3) |
这里α 是同伦参数,vref 是符合实际问题的背景参考值,δ(·)是普通意义的delta函数.当α=1时,罚函数的解就是vref, 能够直接得到精确解,当同伦参数α =0时,罚函数是一个非线性高度不稳定的泛函.事实上,同伦延拓方法是将高度不适定问题和一个适定问题通过同伦参数调节的一种方法,当α 在1附近的时候是非常稳定的,当参数逐渐逼近0 的时候不适定性十分显著,但是,该方法的最大优点就是能够为下一步提供较好的初值.利用梯度法求解罚函数(3)的最小值,即:
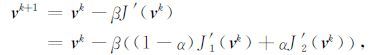
|
(4) |
这里β 是步长调节参数,k是梯度法迭代步数.最主要的难点是计算梯度J′1(v),通过一般的差分方法显然是不切实际的.因此,我们利用对偶法求得,首先给出方程(1)的对偶方程如下:
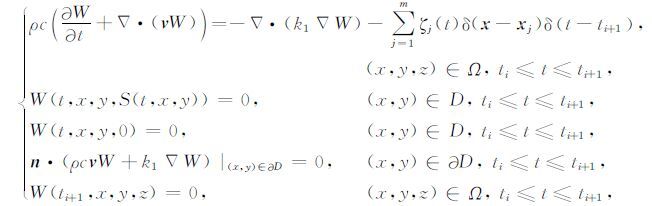
|
J′1(v)可以表示成下面的形式:
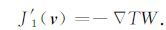
|
同伦参数的选取按照拟Sigmoid函数选取,形式为:
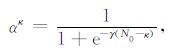
|
其中κ 为同伦延拓算法的迭代步数,γ 为修正步长调整参数,N0 为同伦参数起始估计值,这些参数对于α 的影响可以参见文献[17].利用稳定性较好的不动点同伦映射求解速度场反演问题的步骤如下:
(1) 给定速度场初始值v0 =vref, 设置Sigmoid函数的各个参数值,置迭代步κ =0,vκ =v0;
(2) 对方程(1)进行正演计算,计算结果与第一类测量值进行比较,如果满足Morozov 偏差原则[18],则终止计算,此时vκ 作为反演结果;否则,计算梯度J′1(v);
(3) 根据Sigmoid函数,计算ακ,若κ>1,计算ακ-1;
(4) 利用梯度法(4)进行计算,得到vκ+1;
(5) 对方程(1)进行正演计算,若J1(vκ+1)<J1(vκ),令ακ =ακ+ακ-1,转至步骤(4);否则,置κ=κ+1转至步骤(2).
3.4 当v(t,x)固定,迭代山体表面初始值S(tp, x,y)结合第二类测量数据S(tc, x,y)和方程(2)的正演计算结果S(tN,x,y),构造下面形式的罚函数:
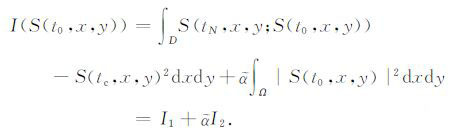
|
(5) |
利用梯度法求解罚函数(5)的最小值,即:
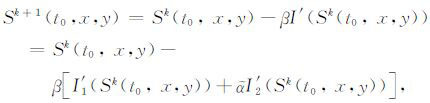
|
(6) |
这里参数$\tilde{a}$,β,k分别表示正则化参数、迭代步长和迭代步数.为了计算I′1(Sk(t0,x,y)),利用对偶方程法求该导数.方程(2)的对偶方程为:
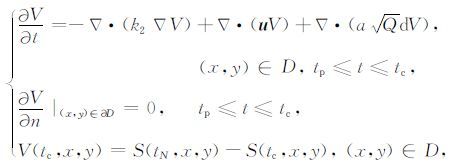
|
通过计算可得I′1(Sk(t0,x,y))=V(tp, x,y).
3.5 HTPM 有限元离散化由于求解HTPM 是在一个任意的三维区域,因此采用文献[19]中的方法进行网格剖分.假设基函数和测试函数分别为{Φi}i=1Nh 和{Ψi}i=1Nd,那么温度场T(t,x)可以表示为

|
在时间轴上,采用欧拉隐格式进行计算,在每个子时间段上分成M等分,ti=t0 <t1 < … <tM-1 <tM=ti+1,这里tn=ti+nτ,τ= (ti+1 -ti)/M,该剖分是为了数值计算进行的剖分.采用标准的有限元方法,基函数选为分片一元多项式,离散后就是下面的代数方程组[20, 21]:
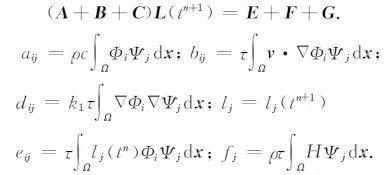
|
SPM 的有限元离散化以及对偶方程的离散化和HTPM 的离散化基本一样,这里不再详细介绍.
4 数值算例通过大量的数值算例表明,如果针对一般的速度场进行反演,得不到很好的结果,有两个主要内在因素:第一个因素是测量数据的有限性,只是在有限的空间点和时间点上有测量数据;第二个因素是反演的未知量是巨大的.因此,在本算例中假设速度的方向是已知的并且反演的速度也是分片常数的情况.物理参数设置为(根据参考文献[3]中数据):
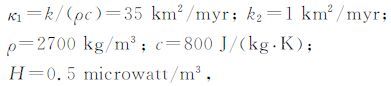
|
这里κ1 表示热扩散系数,myr表示millionyears.
数值参数为:

|
分别表示岩石的历史温度和现在时刻山体表面分布函数.为了提高计算效率,利用Fortran 语言编程,并在实际计算中将矩阵进行了压缩处理(compactrowstorage),求解代数方程组利用QMR(Quasi-minimumresidual)方法进行近似计算,QMR 方法是著名的Krylov子空间迭代算法一种,主要是减少存储空间.为了测试算法的稳定性,在测量数据中加入35dB的随机噪音.山体表面的真实初始值为

|
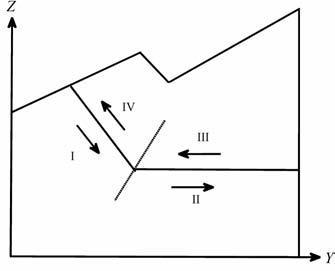
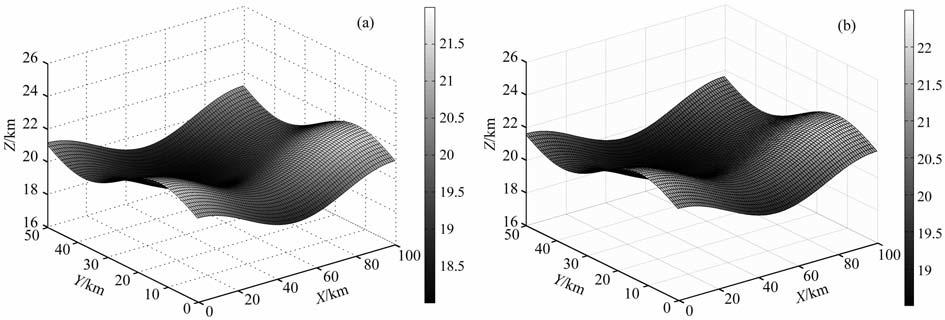
速度的方向和分布示意图如图 1 所示.表 1 和表 2分别为真实速度值和反演速度值.在本数值试验中,速度场X轴分量为零.在整个区域内,速度场的初始猜测值选为(0.0,0.0,0.0),山体表面的初始值的猜测值为S(tp, x,y)=15,(x,y)∈D.图 3表示真实的山体表面分布情况和重构山体表面的分布情况.从表 1、表 2 和图 2 中可以看出,利用同伦延拓算法不仅能够较好地恢复速度场,还能够有效地重构山体表面.重构山体表面的相对误差(L2 范数意义下)为3%.为了和其他算法比较,选取本算例中的初始猜测值,速度场恢复的结果是发散的,不能够得到较好的结果.数值算例还表明,尽管同伦延拓算法对于初值选取有一定的改进,但是,速度场初值的选取严重偏离真实值,那么该算法也有可能发散.另外还有一个有意义的结果,如果选取的初值远离真实值,即使收敛性好,抗噪性也是很差的.相反,如果初值选取比较理想,不仅收敛性能够得到保障还有较好的抗噪性.在实际应用中,地质学家并不是只对山体表面重构的准确性感兴趣,更有意义的是山体的形状.尽管山体表面的准确恢复有很大的困难,可是,如果能够比较好地恢复山体形状也是具有重要地质学意义的结果.虽然本文利用的是比较理想的测量数据,但是,从这些结果可以看出算法的有效性,或者说,比较好的测量数据能够恢复很好的结果.如果实际测量数据十分有限,该算法也极有可能将山体的大体形状有效回复,满足地质学家的实际要求.事实上,实际数据如果不是很充分,可以通过插值技术进行适当扩充,这些数学技术主要是在实际数据处理中体现.
|
图 1 四个分片常数 Fig. 1 Four piecewise constants |
|
|
表 1 真实速度分布(Y方向和Z方向) Table 1 Distribution of true velocity (Y axis and Z axis) |
|
|
表 2 反演速度分布(Y方向和Z方向) Table 2 Distribution of recovering velocity (Y axis and Z axis) |
|
图 2 山体表面分布 (a)真实山体表面;(b)重构山体表面. Fig. 2 Mountain surface proiile (a)True surface profile; (b)Restoring surface profile. |
本文研究了山体表面重构的同伦延拓算法,从数值结果可以看出,算法对于该问题是有效的,不仅具有较好的收敛性还有很好的稳定性.利用对偶方程技术计算罚函数的导数,提高了计算导数的准确性和计算速度,为同伦延拓算法的应用奠定了基础.在数值算例中,将速度场进行了简化,不仅知道速度场的方向而且速度场也只有四个分片常数,这是很简单的情况,但却很有实际的应用价值.从地质学考虑,速度场之间的跳跃可以认为是地壳的断层,而速度场的每个部分可以看成是该区域的速度平均值,小区域的速度变化对山体表面重构的影响和利用速度场的平均值计算的结果基本一样.因此,在数值计算和实际应用中都采用这样的简单形式,既有利于实际操作也能够得到较好的数值结果,这样才会更好地将理论和实际数据解释有效地结合到一起.值得注意的是,在本文中并没有将山体假设为不可压缩的,换句话说,速度场的散度不为零.如果假设山体是不可压缩的,即速度场的散度为零,就可以应用不连续Galerkin方法进行计算,这样就会得到更好的计算结果,这也是下一步要继续研究的重要部分.尽管山体内部的温度场变化还涉及很多化学因素,山体表面运动模型还涉及冰雪堆积和融化因素,但是HTPM 和SPM 模型已经在很多地质学实际计算中取得了成功[2~5, 9](事实上,国内的袁益让等学者对类似的时间和空间大尺度的三维对流扩散方程进行了正演研究[22~25],并将该结果成功应用到胜利油田开发中).据作者所知,还没有针对该耦合模型进行实际数据处理的报道,下一步的工作还要涉及实际数据的处理,并将这些结果应用到石油勘探、地质动力学和大气变化等实际应用领域.
致谢作者衷心感谢在密歇根州立大学留学期间Gang Bao (Michigan State University)and Zheng fu Xu(Michigan State University)给予的数学理论指导,以及ToddA.Ehlers(University of Michigan)给予的地质学指导和Peijun Li(Purdue University)在数值计算方面的大力帮助,本文的一部分Fortran代码来源于Pei jun Li.作者还要感谢在第二届应用地球物理学术研讨会(清华大学主办)上与徐义贤教授(中国地质大学(武汉))关于HTPM 模型的讨论.
| [1] | Braun J. Quantifying the effect of recent relief changes on age-elevation relationships. Earth Planet. Sci. Lett , 2002, 200(3-4): 331-343. |
| [2] | Braun J. Estimating exhumation rate and relief evolution by spectral analysis of age-elevation datasets. Terra Nova , 2002, 14(3): 210-214. DOI:10.1046/j.1365-3121.2002.00409.x |
| [3] | Braun J, van der Beek P, Batt G. Quantitative Thermochronology: Numerical Methods for the Interpretation of Thermochronological Data. UK: Cambridge University Press, 2006 . |
| [4] | Ehlers T A, Chaudhri T, Kumar S, et al. Computational tools for low-temperature thermochronometer interpretation. Rev. Mineral. Geochem , 2005, 58(1): 589-622. |
| [5] | Meesters A G C A, Dunai T J. Sloving the production-diffusion equation for finite diffusion domains of various shapes. Part II. Applications to cases with α-ejection and non-homogeneous distribution of the source. Chemical Geology , 2002, 186(1-2): 57-73. DOI:10.1016/S0009-2541(01)00423-5 |
| [6] | Reiners P W, Ehlers T A, Zeitler P K. Past, present, and future of thermochronology. Rev. Mineral. Geochem , 2005, 58(1): 1-18. |
| [7] | House M A, Farley K A, Kohn B P. An empirical test of helium diffusion in spatite: borehole data from the Otway Basin, Australia. Earth Planet. Sci. Lett , 1999, 170(4): 463-474. |
| [8] | Tomkin J H, Braun J. The influence of alpine glaciation on the relief of tectonically active mountain belts. Am. J. Sci , 2002, 302(3): 169-190. |
| [9] | Ehlers T A, Farley K A. Apatite (U-Th)/He thermochronometry: methods and applications to problems in tectonic and surface processes. Earth Planet. Sci. Lett , 2003, 206(1-2): 1-14. |
| [10] | Reich M, Ewing R C, Ehlers T A, Becker U. Low-temperature anisotropic diffusion of helium in zircon: Implications for zircon (U-Th)/He thermochronometry. Geochim. Cosmochim. Acta , 2007, 71(12): 3119-3130. |
| [11] | Stockli D F, Farley K A, Dumitru T A. Calibration of the apatite (U-Th)/He thermochronometer on an exhumed fault block, White Mountains, California. Geology , 2000, 28(11): 983-986. DOI:10.1130/0091-7613(2000)28<983:COTAHT>2.0.CO;2 |
| [12] | Warnock A C, Zeitler P K, Wolf R A, et al. An evaluation of low-temperature apatite U-Th/He thermochronometry. Geochim. Cosmochim. Acta , 1997, 61(24): 5371-5377. |
| [13] | 傅红笋, 韩波. 二维波动方程速度的正则化-同伦-测井约束反演. 地球物理学报 , 2005, 48(6): 1441–1448. Fu H S, Han B. A regularization homotopy method for the inverse problem of 2-D wave equation and well log constraint inversion. Chinese J. Geophys. (in Chinese) , 2005, 48(6): 1441-1448. |
| [14] | 崔凯, 杨国伟, 李兴斯, 等. 用同伦方法反演非饱和土中溶质迁移参数. 力学学报 , 2005, 37(3): 307–312. Cui K, Yang G W, Li X S, et al. A homotopy method for parameter inversion of solute transport through unsaturated soils. Acta Mechanica Sinica (in Chinese) , 2005, 37(3): 307-312. |
| [15] | 韩华, 魏培君, 章梓茂. 用同伦方法反演流体饱和孔隙介质的参数. 岩石力学与工程学报 , 2004, 23(1): 129–136. Han H, Wei P J, Zhang Z M. Homotopy method for inversing parameters of wave equation in porous media. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2004, 23(1): 129-136. |
| [16] | 韩华, 章梓茂, 汪越胜, 等. 双相介质波动方程孔隙率反演的同伦方法. 力学学报 , 2003, 35(2): 235–239. Han H, Zhang Z M, Wang Y S, et al. Homotopy method for inversing the porosity of 1-D wave equation in porous media. Acta Mechanica Sinica (in Chinese) , 2003, 35(2): 235-239. |
| [17] | 田迎春, 章梓茂, 马坚伟, 等. 黏弹性双相介质参数反演的同伦方法. 地球物理学报 , 2009, 52(9): 2328–2334. Tian Y C, Zhang Z M, Ma J W, et al. Inversing physical parameter of two-phase viscoelastic media by homotopy method. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2328-2334. |
| [18] | Engl H W, Kunisch K, Neubauer A. Convergence rates for Tikhonov regularisation of nonlinear ill-posed problems. Inverse Probl , 1989, 5: 523-540. |
| [19] | Persson P O, Strang G. A simple mesh generator in MATLAB. SIAM Rev , 2004, 46(2): 329-345. |
| [20] | Brenner S C, Scott L R. The Mathematical Theory of Finite Element Methods, 2nd ed. New York: Springer-Verlag, 2002 . |
| [21] | Thomée V. Galerkin Finite Element Methods for Parabolic Problems. New York: Springer-Verlag, 1997 . |
| [22] | Yuan Y R, Wang W Q, Yang D P, et al. Numerical simulation for evolutionary history of three-dimensional basin. Appl. Math. Mech , 1994, 15(5): 435-446. |
| [23] | Yuan Y R. The upwind finite difference fractional steps method for combinatorial system of dynamics of fluids in porous media and its application. Science in China Series A: Mathematics , 2002, 45(5): 578-593. |
| [24] | Yuan Y R. The upwind finite difference fractional steps methods for two-phase compressible flows in porous media. Numer. Meth. Part. D. E , 2003, 19(1): 67-88. |
| [25] | Yuan Y R. The characteristic finite element alternating-direction method with moving meshes and analysis for the numerical simulation of oil-gas resources. J. Sys. Sci. & Math. Scis , 2009, 29(7): 947-961. |
 2011, Vol. 54
2011, Vol. 54




