2. 中国地震局地球物理研究所,北京 100081;
3. 中国石油化工股份有限公司石油物探技术研究院,南京 210014
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China;
3. Geophysical Research Institute, SINOPEC, Nanjing 210014, China
研究地震波在复杂介质中的传播规律,是地球物理学中的一项重要内容,是帮助人们认识地球介质的有效模拟手段.在研究全球尺度的地震波场模拟时,我们关注的是较长时程的地震波计算问题,借此来深入探讨地球深部结构,这就需要选择较为高效、稳定和具有较强长时间模拟能力的数值算法.
常见的正演数值模拟方法,如有限差分法、伪谱法和有限元法等都已比较成熟.有限差分的理论基础是Taylor展开,其特点是计算速度快,计算效率高,但对于高度非规则区域较难处理.有限元法的理论基础是变分原理,构建在Sobolev函数空间上,通过将单位元上的分片插值函数和最小位能理论相结合来求解整个区域的波场信息,但其计算过程复杂,计算量大.伪谱法采用了快速傅里叶变换,使其具有较快的计算速度,但对于复杂介质的地震波模拟结果并不理想.这些数值方法都有一定的适用条件和局限性,尤其是其网格离散化近似的非保结构性质,在一定程度上和一定范围内对波动方程及解的结构的破坏是不可避免的,其数值解对于精确解的偏离也是不可避免的.这一数值方法的固有问题,在一定范围内,显现得不是很突出,从而被认为是有效的数值方法,其计算结果被接纳.但就大尺度、长时程问题而言,其波动方程在时间域处理时,具有很强的时空继承性,其积累误差较为明显,甚至是无法容忍的,导致计算精度无法满足要求.辛算法正是在这样的需求下提出来的,要求在方程进行离散化和有限化近似过程中,尽可能保持运动方程的结构及其相应的守恒量不变,或者,把数值解对于精确解的偏离控制在设定的精度以内,使得辛算法能从根本上提高解的精度和可信度.这一保结构算法思想是冯康首先提出的.冯及其研究小组在哈密顿系统的辛算法构造和理论分析都取得了一系列成果,并且引起了国内外学者的极大兴趣,产生了很多重要的后继成果.计算实验显示,辛算法优异的稳定性和长时间跟踪能力有着重要的应用前景.
辛算法在众多科学计算领域得到了应用和发展.地震波场在高频近似条件下,其射线解刻画了地震波场的射线走向和波阵面形态,这在地震波场传播的渐近解研究、模型研究及波场成像的运用中具有广泛的实用价值.然而,算法本身的一个重大缺陷是在焦散区失效[1],1965 年前苏联学者V.P.Maslov将射线问题转化为辛空间中的Lagrange子流形问题,成功地解决了焦散问题,从而大大拓广了几何光学应用范围.陈景波[2]和高亮[3]等用辛几何算法解决地震射线追踪问题得到了较好的结果,和四阶Runge-Kutta方法相比,精度相当,但辛算法的计算速度较快.在基于波动方程的地震波数值模拟方面,Chen[4]将辛格式和伪谱法相结合求解了标量波波动方程,和非辛格式的算法相比,辛格式显示了较小的误差增长.
本文采用三阶辛格式有限差分对标量波波动方程进行了时间离散,空间离散则采用奇异核褶积微分算子.在20世纪70年代早期,就有学者提出褶积微分算子的概念,但将其应用到地震波场模拟中比较晚.Holberg[5]运用Fourier变换,对褶积微分算子进行了设计,并在三维弹性波数值模拟中取得了较好的结果.Zhou 等[6]、张中杰等[7]和戴志阳等[8]也对这一方法进行了深入研究和发展.龙桂华等[9]在前人的工作基础上,根据函数分布理论,引入奇异核褶积微分算子,通过一组经过加窗处理的微分算子和波场变量进行褶积,来求取波场变量关于空间微分.褶积微分算子和伪谱法相比,其优势在于褶积微分算子可以优化为短算子,更能突出空间微分本身的局部属性;而伪谱法在计算微分时须利用全局信息,就复杂非均匀介质中波的传播问题而言,与物理因果律相悖.褶积微分算子和有限差分算子相比,精度更高,能够弥补有限差分算子描述复杂介质的不足.因此褶积微分算子应用于波动方程的空间离散或空间微分近似是非常有效的.
2 标量波动方程的辛差分格式考虑均匀各向同性介质二维标量波方程
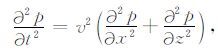
|
(1) |
其中,波场变量p=p(x,z,t),速度场v=v(x,z,t).记微分算子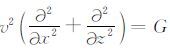
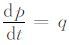
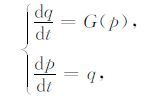
|
(2) |
即
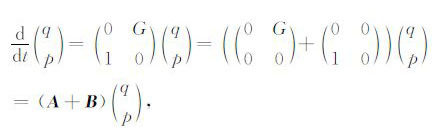
|
(3) |
由附录A 关于辛格式推导,得到

|
(4) |
其中,波场变量的上标表示时间序列中的时间点,Δt表示时间步长,I表示与A,B同阶的单位矩阵.
确定(4)式中系数ci,di,i=1,…,k,Suzuki[10]和Yoshida[11]已经建立起了一般理论,Ruth[12]给出了形式最为简洁的3级3阶显式辛格式,Iwatsu[13]给出了另外两组3级3 阶显式辛格式,其中一组显示了比Ruth 给出的格式更好的稳定性.故本文引用了Iwatsu给出的系数.
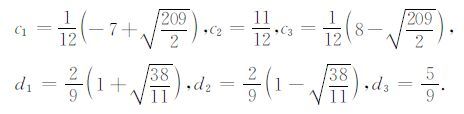
|
根据广义函数理论,在给定的函数空间中的元素f(x)可以定义为核函数和元函数的褶积形式[14]:
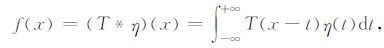
|
(5) |
其中,T(x)是奇异核函数,η(x)为函数空间的元函数.
奇异核函数包括Hilbert 函数、Abel函数和Delta函数.其中,Hilbert函数和Abel函数多见于解析函数理论,而Delta函数常被用于偏微分方程的数值求解方面.Delta函数的形式表示为

|
(6) |
式中,q表示关于x的q阶广义导数.
在数值计算中,需要考虑用近似函数来逼近物理上很难实现的理论Delta函数.选用了归一化的Shannon奇异核函数:
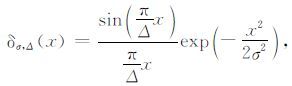
|
(7) |
其中,Δ 为空间步长,σ 为高斯函数包络线宽度.对于任意给定的σ ≠ 0,当Δ→0 时,(7)式趋近于Delta函数.
当已知某函数的离散序列{u(xk)},该函数的微分形式可由奇异核函数的微分来近似:

|
(8) |
其中,W为算子半带宽.W和高斯包络σ 是可变的,适当选取可提高微分的精度.当q=2时,二阶微分算子表示为
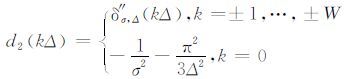
|
(9) |
该褶积微分算子系数δ″σ,Δ(kΔ)=δ″σ,Δ(-kΔ),k=1,…,W.
在实际计算过程中,没有直接运用上述算子,而是进行了加窗处理,借此来有效地抑制由于算子截断而引起的Gibbs效应.选用Hanning窗函数:
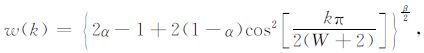
|
(10) |
作用于微分算子,得到处理后的算子:
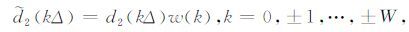
|
(11) |
在这里,选取Hanning 窗函数的参数α = 0.54 和β =8.
4 算法的稳定性条件在时间域地震波场数值模拟中,计算的时间步长与空间离散网格的大小必须满足一定的条件,才能保证迭代计算的可行.如果不满足这些条件,可能产生无物理意义的按指数增大的数值计算结果,造成模拟结果网格频散严重,影响对问题的分析,严重时会造成溢出而使计算无法进行.对一种数值解法,需要知道计算稳定的离散参数区域,即分析解法的稳定性.
在波数域中,(1)式表示为

|
(12) |
记-
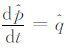

|
(13) |
即

|
令矩阵
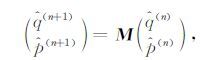
|
(14) |
形如(14)式的差分格式算法稳定的充要条件是矩阵M的谱半径ρ(M)≤1.
经推导,该差分格式应满足的稳定性条件如下:

|
上述条件的具体推导和参数表达式参见附录B.
5 数值实验首先研究了简单的均匀弹性介质模型,将本文的辛算法结果和非辛算法的结果进行比较,这里采用的非辛算法是指时间微分用2 阶中心差分来近似,空间微分采用8阶中心差分来近似,以下未做说明均简称有限差分算法.
模型的物性参数为:波速3000 m/s;模型沿横向和纵向各剖分出256 个网格点,空间间隔均为20m;震源位于模型(2560m, 2560m)处,由主频为30Hz的Ricker子波激发产生;Ricker子波的具体表达式见附录C,时间步长为3 ms.检波器位于(2560m, 2060m)处.
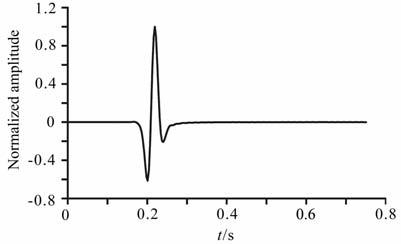
图 1、图 2分别给出了辛算法和有限差分算法在0.75s时刻(第250次时间迭代步)的波场快照,可以看到,辛算法的结果波前面清晰可辨,几乎没有频散,而在相同的参数设置下,有限差分算法的数值频散很明显.图 3、图 4给出了检波器得到的0.75s内的地震记录,可以看到采用有限差分算法的曲线,在首波没有到达之前和之后,都有很强的数值频散.而辛算法的结果几乎没有数值频散.

|
图 1 辛算法均匀介质中0.75s的波场快照 Fig. 1 Snapshot of wavetield in homogeneous mediawith symplectic algorithm at 0.75 s |

|
图 2 有限差分算法均匀介质中0.75s的波场快照 Fig. 2 Snapshot of wavetield in homogeneous media with tinite difference algorithm at 0.75 s |
|
图 3 均匀介质检波器处辛算法的地震记录 Fig. 3 Seismogram in homogeneous media with symplectic algorithm at receiver |

|
图 4 均匀介质检波器处有限差分算法的地震记录 Fig. 4 Seismogram in homogeneous mediawith tinite difference algorithm at receiver |
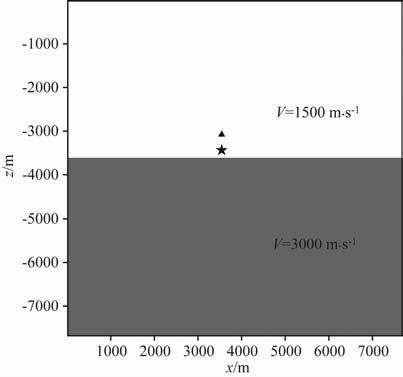
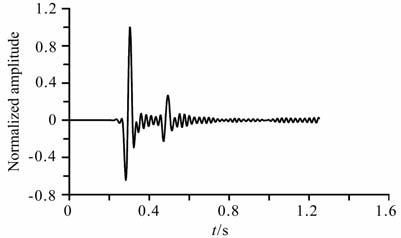
对于更极端的问题,我们进行了高对比度速度分层均匀介质模型的模拟试验,介质分界面位于地下3615m 处,介质上层的速度是1500m/s, 下层的速度是3000m/s.震源位于地下(3840 m, 3465 m)处,由主频为30Hz的Ricker子波激发产生.时间间隔为2.5ms, 空间间隔为15m, 模型沿横向和纵向各剖分512个网格点.检波器位于(3840m, 3090m)处.
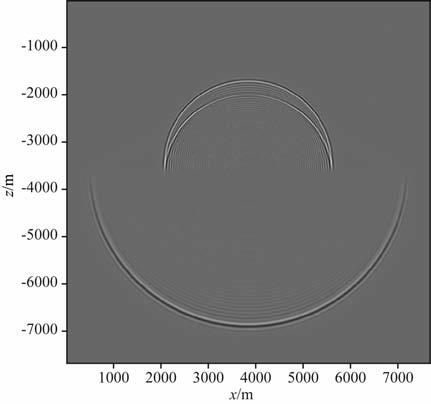
图 5给出了该分层均匀介质模型,五角星表示震源所在位置,三角形为检波器所在位置.图 6和图 7分别给出了辛算法和有限差分算法在1.25s时刻(第500次时间迭代步)的波场快照.辛算法和有限差分算法的结果,差别是很明显的,辛算法的结果直达P波和反射P波的波前都很清晰,而有限差分算法的波前扰动较为明显,尤其是在上层介质中反射P波的周围,从而较好地反映出辛算法的优势.图 8、图 9给出了检波器得到的1.25s内的地震记录,可以看到采用有限差分算法的曲线,在首波没有到达之前和之后,都有很强的数值频散.而辛算法的结果中数值频散得到了很好的抑制.
|
图 5 分层均匀介质模型 Fig. 5 Homogeneous layered model |

|
图 6 辛算法分层均匀介质中1.25s的波场快照 Fig. 6 Snapshot of wavefield in homogeneous layered media with symplectic algorithm at 1.25 s |
|
图 7 有限差分算法分层均匀介质中1.25s的波场快照 Fig. 7 Snapshot of wavefield in homogeneous layered media with finite different algorithm at 1.25 s |
|
图 8 分层均匀介质检波器处辛算法的地震记录 Fig. 8 Snapshot of waveiield in homogeneous media with symplectic algorithm at receiver |

|
图 9 分层均匀介质检波器处有限差分算法的地震记录 Fig. 9 Seismogram in homogeneous layered media with finite difference algorithm at receiver |
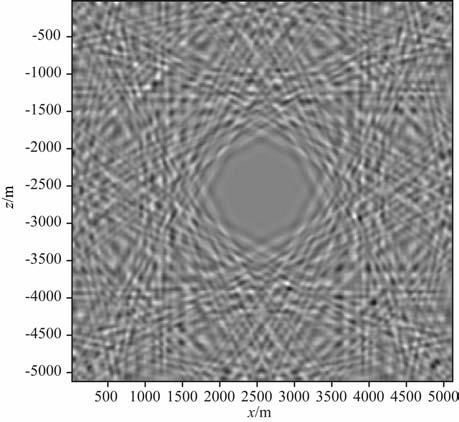
为了检验本文提出的算法的保结构特性,我们对一个均匀介质模型的波场情况进行了长时程的跟踪,模型界面没有加任何边界条件.模型的物性参数为:波速3000m/s;模型沿横向和纵向各剖分出256个网格点,空间间隔均为20m;震源位于模型(2560m, 2560m)处,由主频为30Hz的Ricker子波激发产生;时间步长为3 ms.图 10 和图 11 分别给出了辛算法和有限差分算法在第5000次时间迭代步,即第15s时刻的波场快照,可以看到,由辛算法模拟的波前面十分清晰,而从有限差分算法的结果中,已经很难辨清波前的形状了.由此可知,本文提出的方法具有较明显的保结构性,适合处理高精度、长时程波场模拟.
|
图 10 辛算法均匀介质中15s的波场快照 Fig. 10 Snapshot of wavefield in homogeneous media with symplectic algorithm at 15s |

|
图 11 有限差分算法均匀介质中15s的波场快照 Fig. 11 Snapshot of wavefield in homogeneous media with finite difference algorithm at15 s |
本文给出了用于地震标量波场模拟辛格式奇异褶积微分算子方法,以及该算法的稳定性分析.该算法在计算过程中,存储较少,易于实现,虽然相比本文用于对比的非辛有限差分格式,增加了一些计算迭代步骤和时间,但在抑制频散和提高精度方面都有明显改善,并且具有较强的稳定性.在本文给出的算例当中,辛算法的计算耗时约是有限差分算法的2.6倍,但当计算长时程问题时,计算效率较短时程问题有所提高.也就是说,时程越长,越能体现辛算法的优势.因此,辛算法可以在一定范围内加大时间和空间步长、提高计算效率,能够作为研究大尺度、长时程的地震波场模拟的有效方法.
附录A
考虑Hamilton系统
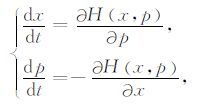
|
(A1) |
令z= (x,p),引入Possion 括号{},其定义为{F,G}=FxGp-FpGx,并引入微分算子DG,定义DGF = {F,G},(A1)式可以写为

|
(A2) |

|
(A3) |
若存在实数ci,di,i=1,2,…,k,使得
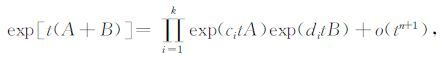
|
(A4) |
由于exp(ditA),exp(citB)均为辛变换[3],则可得(A3)式的n阶辛格式

|
(A5) |
(A5)式离散化,并用Taylor展开得到
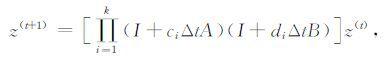
|
(A6) |
写成如下形式,即为单步k级n阶显式辛格式,
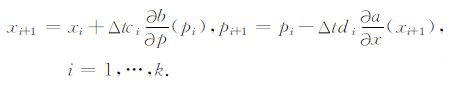
|
(A7) |
附录B
利用本文引入的褶积微分算子,可得函数u(x)二阶微分的离散近似表达式:

|
(B1) |
将(B1)式两边进行Fourier变换,并由算子系数的对称性,得到

|
(B2) |
取kx=$\frac{\pi }{\Delta x}$,得到

|
(B3) |
考虑正文中(14)式差分格式
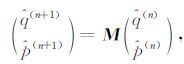
|
(B4) |
其算法稳定的充要条件是矩阵M的谱半径ρ(M)≤1.
由于矩阵M中的每一级步进变换都是辛变换,所以,可以验证det(M)=1[19].
矩阵M的特征值λ 满足特征方程
λ2 -tr(M)λ+det(M)=0,即可改写为
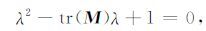
|
(B5) |
由稳定性条件,要求|tr(M)|≤2即可.
取Δx= Δz=Δ,令
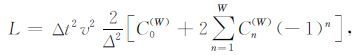
|
得到
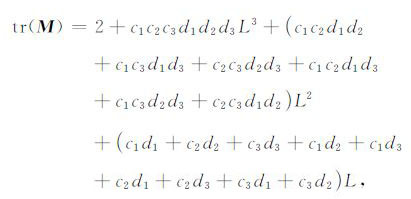
|
(B6) |
整理

|
(B7) |
其中,
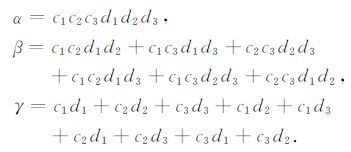
|
进一步,得到
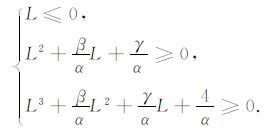
|
(B8) |
(B8)式中的一元三次不等式,由Cardano 公式,得到其解,L≥L1,其中,
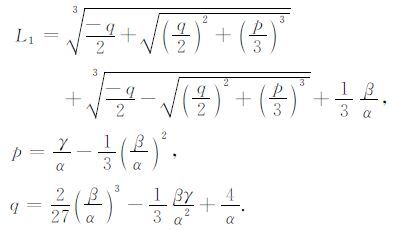
|
附录C
本文运用非零相位的Ricker子波作为震源时间函数,其函数表达式为
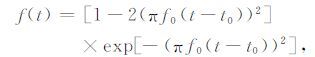
|
(C1) |
其中,f0 为Ricker子波的峰值频率,t0 为起震的时间延迟.
| [1] | 李世雄. 波动方程的高频近似与辛几何. 北京: 科学出版社, 2001 . Li S X. The High-Frequency Approximation of Wave Equations and Symplectic Algorithm (in Chinese). Beijing: Science Press, 2001 . |
| [2] | 陈景波, 秦孟兆. 辛几何算法在射线追踪中的应用. 数值计算与计算机应用 , 2000, 21(4): 255–265. Chen J B, Qin M Z. Ray tracing by symplectic algorithm. Journal of Numerical Methods and Computer Applications (in Chinese) , 2000, 21(4): 255-265. |
| [3] | 高亮, 李幼铭, 陈旭荣, 等. 地震射线辛几何算法初探. 地球物理学报 , 2000, 43(3): 402–410. Gao L, Li Y M, Chen X R, et al. An attempt to seismic ray tracing with symplectic algorithm. Chinese J. Geophys. (in Chinese) , 2000, 43(3): 402-410. |
| [4] | Chen J B. Lax-Wendroff and Nystrm methods for seismic modeling. Geophysical Prospecting , 2009, 57(6): 931-941. DOI:10.1111/gpr.2009.57.issue-6 |
| [5] | Holberg O. Computational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena. Geophysical Prospecting , 2006, 35(6): 629-655. |
| [6] | Zhou B, Greenhalgh S. Seismic scalar wave equation modeling by a convolutional differentiator. Bull. Seism. Am , 1992, 82(1): 289-303. |
| [7] | 张中杰, 滕吉文, 杨顶辉. 声波与弹性波场数值模拟中的褶积微分算子法. 地震学报 , 1996, 18(1): 63–69. Zhang Z J, Teng J W, Yang D H. The convolutional differentiator method for numerical modeling of acoustic and elastic wave-field. Acta Seismologica Sinica (in Chinese) , 1996, 18(1): 63-69. |
| [8] | 戴志阳, 孙建国, 查显杰. 地震波场模拟中的褶积微分算子法. 吉林大学学报(地球科学版) , 2005, 35(4): 520–524. Dai Z Y, Sun J G, Cha X J. Seismic wave field modeling with convolutional differentiator algorithm. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2005, 35(4): 520-524. |
| [9] | 龙桂华, 李小凡, 张美根. 基于Shannon奇异核理论的褶积微分算子在地震波场模拟中的应用. 地球物理学报 , 2009, 52(4): 1014–1024. Long G H, Li X F, Zhang M G. The application of convolutional differentiator in seismic modeling based on Shannon singular kernel theory. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 1014-1024. |
| [10] | Suzuki M. General theory of higher-order decomposition of exponential operators and symplectic integrators. Phys. Lett. A , 1992, 165(5-6): 387-395. |
| [11] | Yoshida H. Construction of higher order symplectic integrators. Phys. Lett. A , 1990, 150(5-7): 262-269. |
| [12] | Ruth R D. A canonical integration technique. IEEE Transactions on Nuclear Science , 1983, 30(4): 2669-2671. DOI:10.1109/TNS.1983.4332919 |
| [13] | Iwatsu R. Two new solutions to the third-order symplectic integration method. Phys. Lett. A , 2009, 373(34): 3056-3060. |
| [14] | Wei G W. Discrete singular convolution for the solution of the Fokker-Planck equation. J. Chem. Phys , 1999, 110(18): 8930-8942. |
| [15] | 黄志祥, 沙威, 吴先良, 等. 高阶辛算法的稳定性与数值色散性分析. 计算物理 , 2010, 27(1): 82–88. Huang Z X, Sha W, Wu X L, et al. Stability and numerical dispersion of high order symplectic schemes. Chinese Journal of Computational Physics (in Chinese) , 2010, 27(1): 82-88. |
| [16] | Hirono T, Lui W, Seki S, et al. A three-dimensional fourth-order finite-difference time-domain scheme using a symplectic integrator propagator. IEEE Transactions on Microwave Theory and Techniques , 2001, 49(9): 1640-1648. DOI:10.1109/22.942578 |
| [17] | Sha W, Huang Z X, Wu X L, et al. Total field and scattered field technique for fourth-order symplectic finite-difference time-domain method. Chinese Physics Letters , 2006, 23(1): 103-105. DOI:10.1088/0256-307X/23/1/030 |
| [18] | Van de Vyver H. A symplectic Runge-Kutta-Nystrm method with minimal phase-lag. Physics Letters A , 2007, 367(1-2): 16-24. DOI:10.1016/j.physleta.2007.02.066 |
| [19] | Dopico F M, Johnson C R. Complementary bases in symplectic matrices and a proof that their determinant is one. Linear Algebra and Its Applications , 2006, 419(2-3): 772-778. DOI:10.1016/j.laa.2006.06.014 |
| [20] | 董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究. 地球物理学报 , 2000, 43(6): 856–864. Dong L G, Ma Z T, Cao J Z. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese) , 2000, 43(6): 856-864. |
| [21] | Kong L H, Liu R, Zheng X H. A survey on symplectic and multi-symplectic algorithms. Applied Mathematics and Computation , 2007, 186(1): 670-684. DOI:10.1016/j.amc.2006.08.012 |
 2011, Vol. 54
2011, Vol. 54

