State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu 610059,China
生物礁滩储层与常规砂、泥岩储层在孔隙结构和地球物理响应特征上有着很大的区别.常规砂、泥岩沉积主要由风化剥蚀的碎屑颗粒经搬运沉积,后经各种成岩作用而形成的一类岩石[1];而生物礁滩储层是由固着生物所形成的原地沉积的碳酸盐岩建造.由于组成常规砂、泥岩储层的岩石组分相对生物礁滩储层的岩石组分较稳定,不易被成岩作用改造,且由于形成砂、泥岩储层的颗粒往往经过了较长时间的搬运,分选较好,因此砂、泥岩储层的颗粒相对稳定和均匀,孔隙几何形状相对单一;而生物礁滩储层的岩石组分由于更易受后期成岩作用的影响,且基本不经过搬运与分选,因此使其储集空间演化复杂,孔隙类型多样,横向变化快,同一储集层内往往存在多种类型的孔隙.
目前对于干燥岩石孔隙结构的模拟主要采用三种模型[2]:(1)Hudson 椭球裂隙型岩石物理模型,但其主要适用于裂缝孔隙度小于0.12 的情况.(2)1949年Mindlin 讨论了颗粒接触后岩石受到的剪切应力的情况,推广了赫兹接触模型,形成了HertzMindlin模型,通过实验,对经过压实的颗粒状岩石,特别是对于物性变化比较均匀的碎屑岩,该模型提供了很好的描述;(3)Eshelby1957年提出的埃瑟比椭球包体裂缝理论,可以有效地描述由岩石基质和气体组成的两相体岩石,适合干燥多孔岩石的情况.但是由于孔隙流体对岩石弹性有较大的影响,因此专门建立了描述饱和岩石的Gassman 方程(Gassman, 1951),但是由于需要描述岩石的参数太多,条件过于苛刻,在实际应用中较难实现.目前国内外对岩石内部孔隙结构的研究主要从理论岩石物理模型的测试分析、实际地层岩样的测试和测井数据入手,进行孔隙形状、孔隙大小与岩石二相体等效参数间的关系研究.贺振华等人针对不同类型的裂缝和孔洞模型进行了岩石物理模型试验[3],在此基础上还对含裂缝的介质进行波动方程数值模拟,以期找到不同裂缝类型时的地震响应特征,从而对其进行预测.在测井上主要用核磁共振(NMR)评价储层孔隙结构[4-6],研究成岩作用对孔隙结构和孔隙大小的影响[7, 8],以及孔隙形状、孔隙大小、孔隙流体与岩石等效弹性参数间关系的研究[9-12].
目前广泛应用的储层物性横向预测技术已经有很多研究实例[13-18].比较常用的孔隙度预测方法主要从以下几方面来讨论:(1)对岩性比较单一,横向变化不大的地区,直接用Wyllie 时间平均方程或Raymer方程进行孔隙度预测;(2)基于地震单属性和多属性多元线性回归法、神经网络法、随机模拟法等多种孔隙度预测方法[14, 17];(3)通过非线性储层岩石物性褶积模型,建立波阻抗与孔隙度与泥质含量的关系,反演出孔隙度[15].由于以上几种方法都是从测井上或有限的岩样统计出发,建立地震的各种属性与孔隙度的关系,反演出孔隙度,很少从理论上讨论影响孔隙度大小的内在因素,在纵向、横向非均质性较强的生物礁滩储层中,应用这种关系进行预测难免存在误差累积效应,最终导致孔隙度预测误差较大,造成对储层孔隙性能的错误认识.本文正是根据目前的岩石物理理论在描述复杂岩性内部孔隙结构的这些缺陷,通过理论和实践的结合,利用岩石薄片和岩石物理测试深入分析和研究了生物礁滩储层孔隙结构的特点,在合理的假设前提下,推导和建立了生物礁滩储层孔隙度与各岩石弹性参数间的关系式.经实际资料验证,该方法可以较有效地描述生物礁滩储层孔隙度的变化.
2 生物礁滩储层孔隙结构模拟的理论基础岩石是由固体的岩石骨架和可流动的孔隙流体组成的二相体.岩石弹性参数一方面受到组成岩石骨架的矿物性质的控制,更重要的是要由岩石内部的孔隙大小、孔隙的几何形状和孔隙流体所决定.为了描述岩石二相体的力学特性,常常引进等效体的概念,即设想一个均匀无孔隙的物体,它的力学性质与两相岩石一致,这个均匀物体的力学参数称为岩石的有效参数,显然这个有效参数取决于孔隙的大小、形状以及岩石基质和孔隙流体的弹性参数的大小[2].
2.1 描述饱和岩石二相体弹性参数关系的Gassman方程孔隙流体对岩石的弹性有很大的影响.如岩石二相体的压缩系数β,对于空气而言,β 趋于无穷大;对于水而言,β值大约为500×10-6MPa-1;对于一般原油的β,则为1000×10-6MPa-1到2500×10-6 MPa-1之间.因此孔隙流体对岩石二相体的压缩系数影响较大[19].
考虑一个外部受到流体静压力(围压)p的作用,内部孔隙压力为pp 的岩石.在外部围压p发生变化时,孔隙体积必然被压缩,因为孔隙流体不能向外流出,所以孔隙压力必然要随围压的变化而变化.我们把这种情况下的岩石二相体的压缩系数记为β.Gassman方程得到了β 与岩石基质、孔隙流体弹性参数之间的关系.
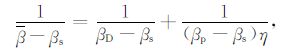
|
(1) |
(1) 式将岩石二相体的孔隙度η、孔隙流体的压缩系数βp、岩石基质的压缩系数βs、排水岩石的压缩系数βD 和不排水的即饱和岩石的压缩系数β 联系了起来,只要知道其中的任意4个量,第5个量便可以由它求出.
2.2 描述干燥岩石弹性参数关系的Eshelby椭球包体裂缝理论岩石二相体的弹性参数除了受岩石骨架和孔隙流体的影响,孔隙的形状也是影响其变化的重要因素.我们把干燥的岩石二相体设想成一均匀的无孔隙的固体,其弹性性质与二相体的岩石一致,令这个均匀体的有效压缩系数为βD.岩石中的孔隙可以分为孔洞和裂缝两类.裂缝类孔隙可以用一个弹性的椭球来模拟,埃瑟比于1957年讨论的Eshelby椭球包体裂缝理论,假定(1)岩石基质是完全各向同性体,其弹性参数为Ks 和us;(2)基质中存在着一个弹性的椭球形包体,包体的几何形状已知,可以是各向异性的;(3)围体(基质)比包体大很多,则边界条件无限远处应变是均匀的[3].1965 年沃尔什(Walsh, 1965)在此基础上推导并得出了干燥多孔岩石基质和包体组成的二相体岩石的等效弹性参数[2].
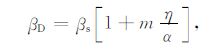
|
(2) |
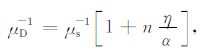
|
(3) |
βD 和μD 分别为干燥岩石二相体的压缩系数和剪切模量,βs 和μs 分别为干燥岩石二相体岩石骨架的压缩系数和剪切模量,α 是孔隙的纵横比,η 为孔隙度.其中
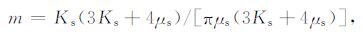
|
(4) |
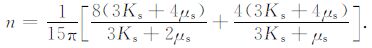
|
(5) |
我们运用Gassman 方程与Eshelby 椭球包体裂缝理论在合理的假设前提下推导和建立了岩石二相体弹性参数间的一个比较实用的新关系式.重写Gassman方程(1):
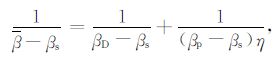
|
(6) |
由于气体β趋于无穷大,水β值大约为500×10-6 MPa-1,一般原油的β为1000×10-6MPa-1到2500×10-6 MPa-1之间,即βp≥500×10-6 MPa-1.而礁滩储层岩石基质的压缩系数βs 一般在15×10-6MPa-1左右,因此βp-βs≈βp.式(6)可以简化为
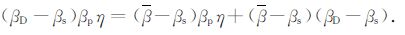
|
(7) |
由式(7)可以得到:
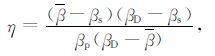
|
(8) |
对于排水情况,压缩系数βD 定义为
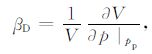
|
(9) |
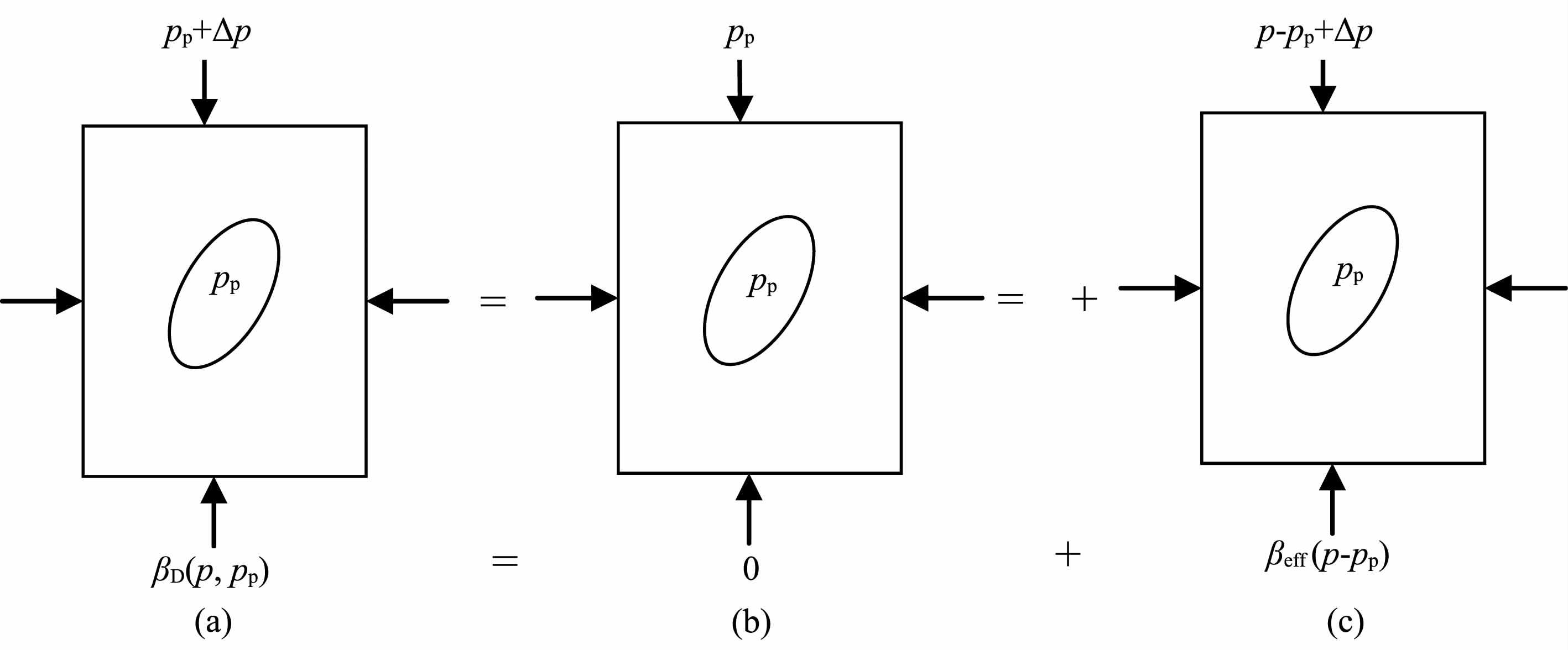
若岩石外部受到流体静压力p,内部受孔隙压力pp的作用,在保持pp 不变的情况下,流体静压力p单位增量的变化Δp导致的岩石体积应变就是排水情况下岩石的压缩系数.首先设想岩石外部和孔隙内部都受到不变的压力pp 作用.显然这种情况不会使岩石体积发生变化(因为压力pp 不变)(图 1b).然后考虑岩石外部作用流体静压力p-pp, 而孔隙内部没有任何压力,这相当于岩石干燥的情况.当外部静压力由p-pp 变到p-pp+Δp时,岩石的体积变化ΔVc 可以由干燥岩石的沃尔什公式给出,为βeff(p-pp)(图 1c),这两种情况的叠加即为我们要求的排水情况下的压缩系数βD (图 1a),则有:

|
(10) |
即排水情况下弹性参数与干燥情况下相同[2].由于βD 在(2)式和(8)式中具有相同的涵义,均为干燥岩石(或不排水岩石)的压缩系数,因此可将(2)式代入(8)式,得:
|
图 1 排水情况下岩石的压缩系数 Fig. 1 The compression coefficient of rocks under drainage situation |

|
(11) |
化简(11)式可以得到:

|
(12) |
则
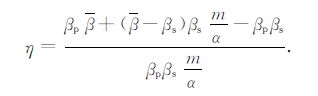
|
(13) |
令C=α/m,简化(13)式可以得到:
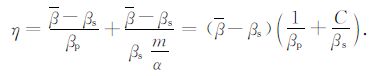
|
(14) |
经岩石物理测试和对岩石薄片的统计分析α/m=C的值可具体求得,若C值近似等于1,则(14)式可进一步简化为
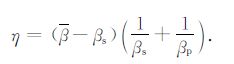
|
(15) |
由于岩石基质的压缩系数βs 一般在15×10-6 MPa-1,而孔隙流体的压缩系数βp 大于500×10-6 MPa-1,只要C大于0.1,则可得近似式:
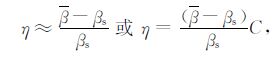
|
(16) |
按压缩系数的定义:

|
(17) |
当目标区域的岩石为干燥岩石(含气)时,β=βD;当目标区域的岩石为饱含油或饱含水时,β =β.由(16)式和(17)式可得:
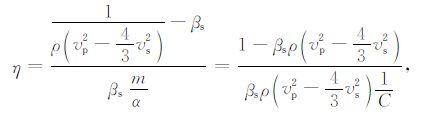
|
(18) |
(18) 式中的βs、C在同一研究区可近似为一常数,可由岩石物理或测井数据统计、计算出来,vp、vs 和ρ可以根据叠前弹性反演直接得到,因此由(18)式可以根据具体研究区的实际地质情况较为准确地计算出目标区域的孔隙度.
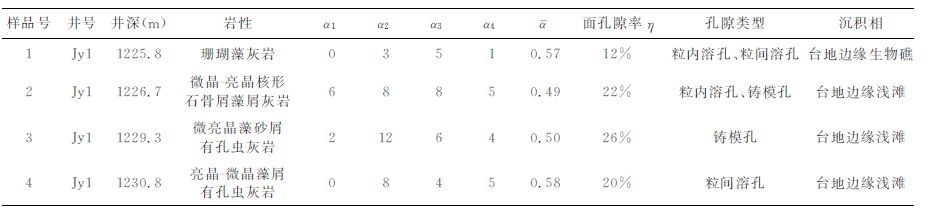
3 岩石物理测试和测井分析(18) 式描述了孔隙度(η)与C、vp、vs 和ρ 之间关系,如何准确地求取这些参数,是成功预测孔隙度的关键.下面将根据实际资料进行岩石物理分析和模型的试算,并以生物礁滩储层为例,验证公式的有效性.该类岩石的孔隙形态主要有以下几种:(1)原生粒间孔、剩余原生粒间孔、生物体腔孔隙等原生孔隙;(2)粒间溶孔、粒内溶孔、铸模孔等次生孔隙;(3)构造缝、压溶缝、溶蚀缝等裂缝孔隙.由于纵横比(α)较小的裂纹,难以成为流体的有效储集空间,因此我们在统计岩石的孔缝形态时,α 值很小的孔缝不参与统计.
3.1 孔隙纵横比(α)和参数m的确定孔隙的几何形态可利用显微镜下的岩石薄片,用人工方法统计.具体的统计方法如下:
图 2的绿色部分为岩石孔缝,孔隙形态用椭圆来逼近,图中α 为椭圆的短轴b与长轴a的比值,即α=b/a.在同一个样品中,对不同大小的α 值进行分组统计,α 为0~0.25范围内的孔隙个数称为α1;α为0.25~0.5范围内的孔隙个数称为α2;α 为0.5~0.75范围内的孔隙个数称为α3;α 为0.75~1.0 范围内的孔隙个数称为α4.αj为同一样品中孔隙纵横比的加权平均值(见表 1).为保证精度,岩性相同的岩石样品要取多块并分别统计各块岩样的平均值,最后通过加权平均,得到总平均值珔α.其统计公式如下:

|
图 2 显微镜下的岩石薄片 Fig. 2 Rock thin section under microscope |
|
|
表 1 岩石薄片孔隙纵横比的统计 Table 1 The statistics of the thin sections′ aspect of pores |
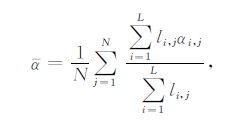
|
(19) |
式中N为岩石样品的个数,L是每个岩石样品中统计α 值的分组数,li为各组αi的个数.
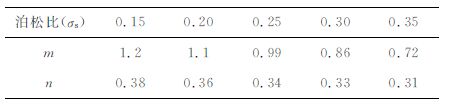
根据公式(4)可以看出,参数m与岩石骨架的剪切模量和体积模量有关,即m的值是由构成岩石的矿物成分与其所占的百分比确定,在一个较小的沉积层序内,可以认为沉积环境比较稳定,沉积岩石的矿物成分与所占的百分比近似为一个常数,因此参数m可以认为是表征岩石基质性质的一个常数.表 2是通过测定具有不同泊松比的岩石的体积模量与剪切模量,计算得到的不同泊松比时参数m的值.由于计算m的公式十分复杂,可以根据已知地区研究目的层段的岩石物理测试数据和测井资料计算出一个平均的泊松比值,再根据表 2 中对应的泊松比近似地确定参数m的大小.
|
|
表 2 不同岩石基质泊松比(σs)时m、n的值 Table 2 The value of m,n indifferent Poisson′s ratio of rock matrix |
根据前面的定义,参数C是孔隙纵横比(α)与参数m的比值,该值的大小直接影响最终结果的正确性.参数m因为只与岩石基质有关系,因此可以近似认为是一个常数;而孔隙纵横比(α)是与孔隙形状有关的一个变量,不同的孔隙形状,其值α 可以变化很大,对最后的结果影响也很大.
根据表 2对参数m的讨论,可以近似得出0.72<m<1.2.当α >0.12时,参数C=m/α>0.1,可以完全满足(16)式的假设条件,说明本文推导的(18)式可以用于预测生物礁滩储层的孔隙度;当α <0.072时,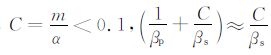
对于生物礁滩储层来说,特别是孔洞型的生物礁滩储层,当孔隙纵横比α 较小时(小于0.072),此时的孔隙基本上为很细小的微裂缝,从储层的角度来说,并不具有实际的勘探意义;而当孔隙纵横比α较大时(大于0.12),此时可以完全满足本文推导公式的应用条件,且此时的孔隙一般孔渗性较好,可以形成比较有勘探价值的生物礁滩储层.
3.3 模型试算与误差分析我们首先分别用岩石物理测试数据和测井数据进行模型试验,验证上述理论的正确性和实用性,然后用常规的孔隙度预测方法对比,验证其效果.
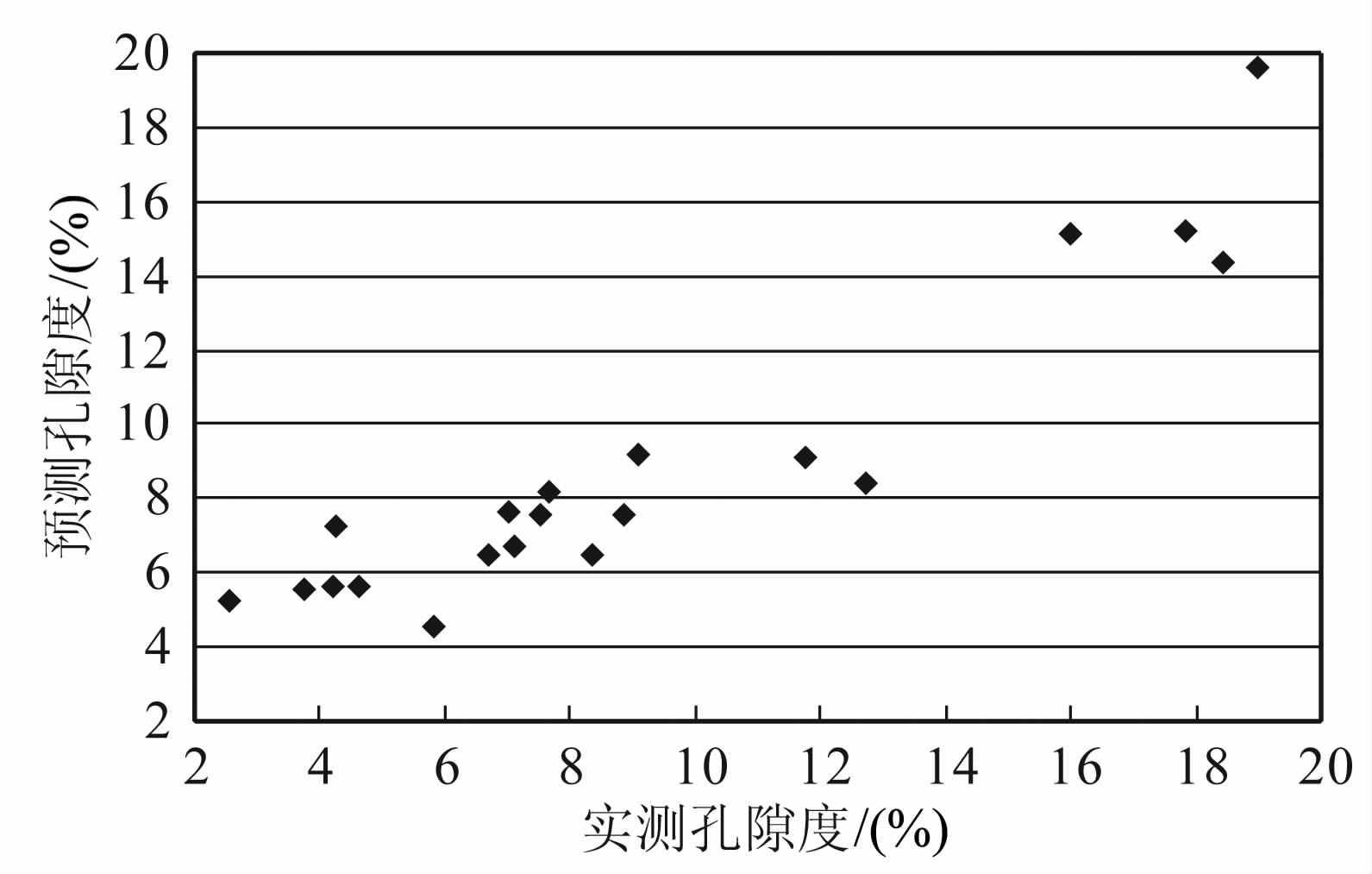
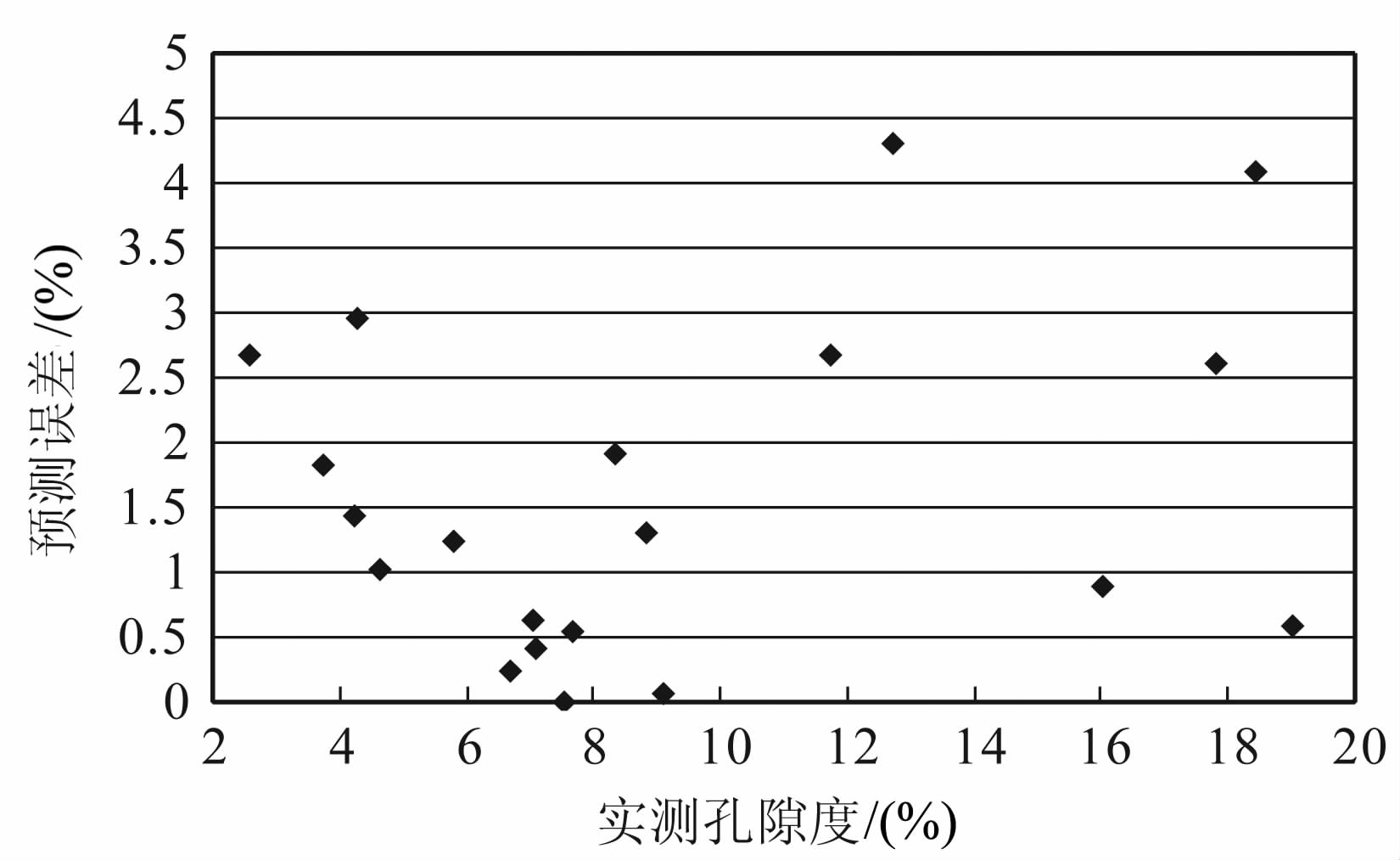
模拟地层温压环境下对研究区目的层段的21个岩样进行岩石物理测试.首先取α =0.535,m=0.86,岩石基质压缩系数βs 可以根据岩样在地层温压环境下实测弹性参数代入(2)式计算得到,这里的βs 代表的是研究区所有岩样基质压缩系数的一个平均值,然后把每块岩样实测的纵波速度、横波速度、密度代入公式(18),最后计算出了21块岩样的孔隙度.图 3和图 4分别为实测孔隙度和预测孔隙度交会图与孔隙度预测误差分布图.从图 3可以看出,预测的孔隙度和实测的孔隙度吻合较好;从图 4 可以看出不同孔隙度时的预测误差分布,21块岩样的整体最大误差小于4.5%,平均绝对误差为1.73%,预测效果较为理想.
|
图 3 实测孔隙度和预测孔隙度交会图(岩石物理) Fig. 3 Cross plot of the measured porosity and the estimated porosity (rock physics) |
|
图 4 实测孔隙度和预测误差的交会图(岩石物理) Fig. 4 Cross plot of the measured porosity and estimated errors (rock physics) |
为了验证该方法的应用效果和适用范围,我们选取了同一地区的两口井Jy1、Jy2的测井数据和不同地区的一口钻井Ky1的测井数据进行试验.首先应用岩石薄片统计获得的参数m/α的值和Jy1井的测井数据计算出该地区的一个平均岩石基质压缩系数βs, 把获得的这些参数带入Jy2井,根据Jy2的纵波速度、横波速度和密度预测出Jy2井的孔隙度;然后用常规的方法预测出Jy2 井的孔隙度,这里是用Jy1井的纵波速度与孔隙度的交会图拟合出它们的一个关系式,把这个关系式用到Jy2井,预测出Jy2井的孔隙度;最后把得到的参数与关系式应用到其他地区的礁滩相储层,说明其适用范围.
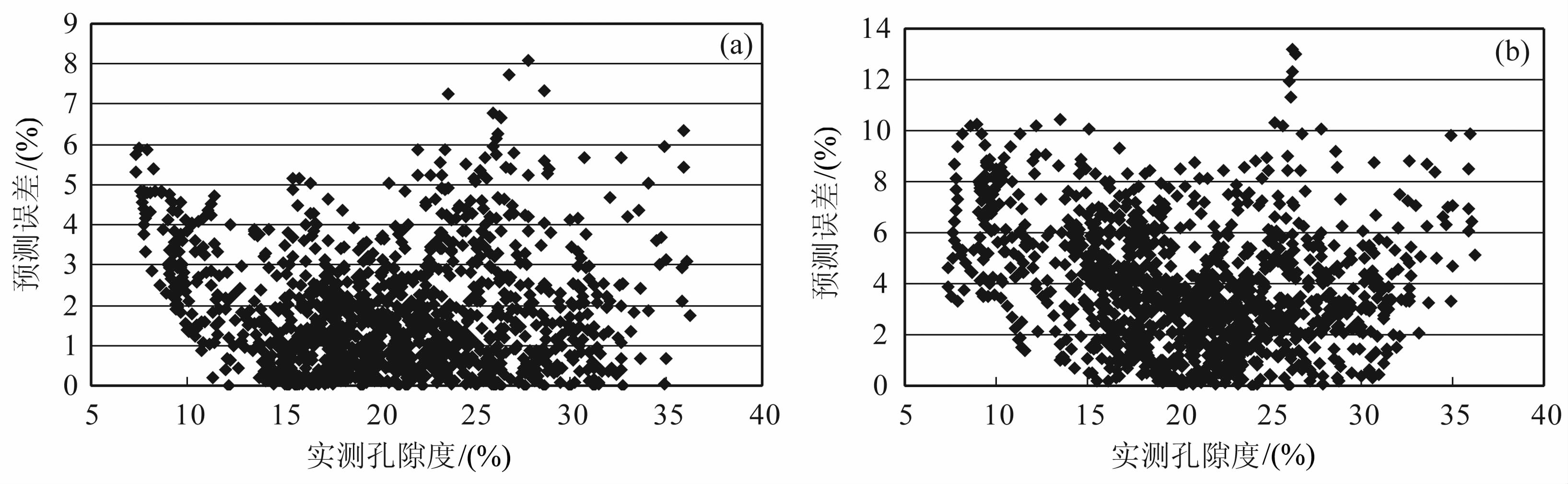
图 5a是用本文论述的方法制作的实测孔隙度和预测误差的交会图,图 5b是常规方法制作的实测孔隙度和预测误差的交会图.经计算,基于岩石物理模型模拟推导的公式预测的孔隙度的平均绝对误差为1.819%,而用常规方法预测的孔隙度的平均绝对误差为3.87%,提高了2%,有效地提高了孔隙度预测的精度.
|
图 5 Jy2井实测孔隙度和预测误差的交会图(a)新方法;(b)常规方法. Fig. 5 Jy2 well:cross plot of the measured porosity and estimated errors (a) New method;(b) Conventional method. |
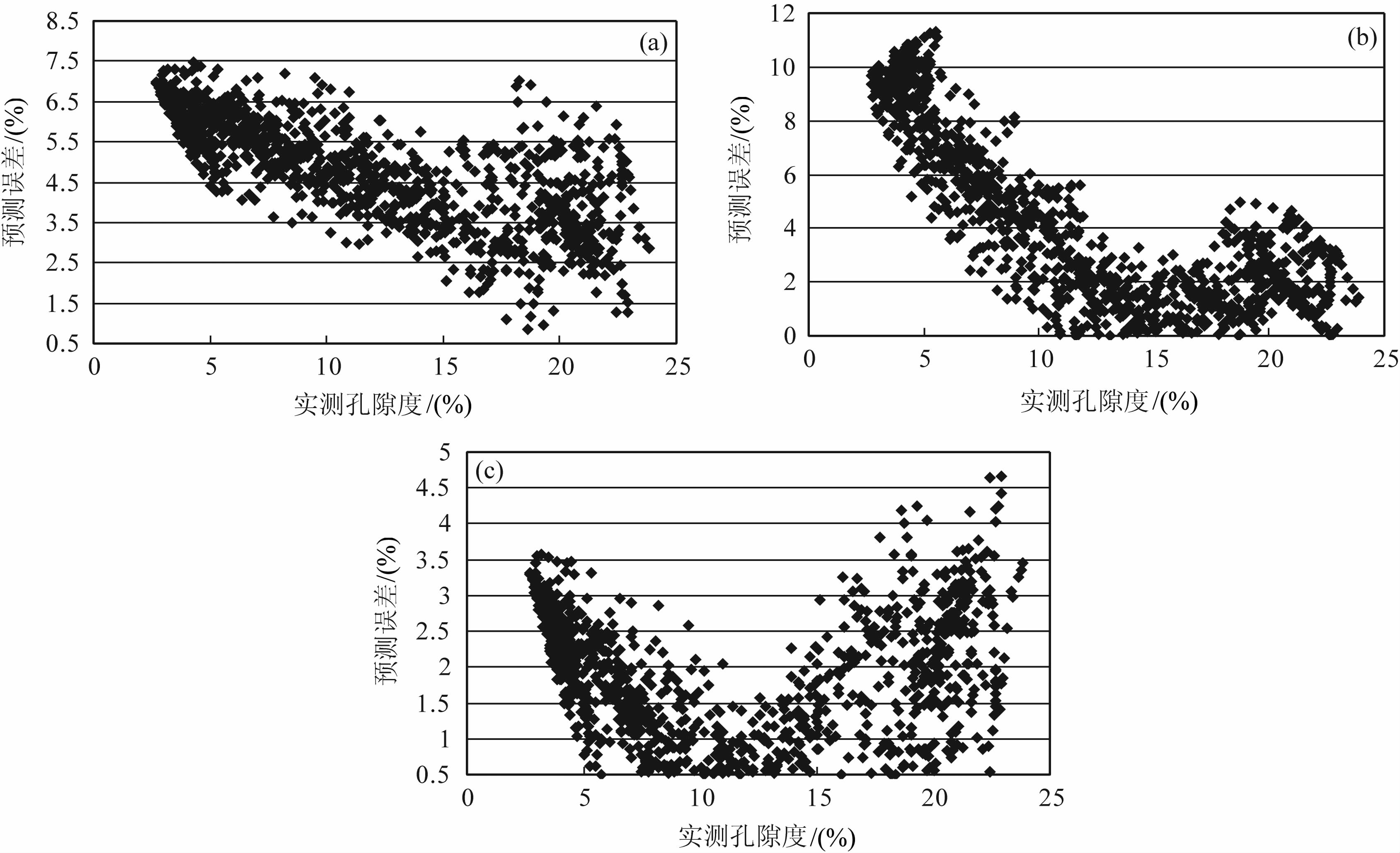
图 6a为不同地区用本文论述的方法制作的Ky1井实测孔隙度与预测误差的交会图,图 6b为常规方法制作的实测孔隙度与预测误差的交会图.经计算,用岩石物理模型模拟推导的公式预测的平均绝对误差为4.823%,而用常规方法预测的孔隙度的平均绝对误差为4.188%.由于该方法应用到其他地区时,误差较大,需对预测公式加以改造.
|
图 6 Ky1井实测孔隙度和预测误差的交会图(a)新方法;(b)常规方法;(c)新方法结果校正之后. Fig. 6 Ky1 well:cross plot of the measured porosity and the estimated errors (a) New method;(b) Conventional method;(c) The result of new method after region corrected. |
经试验发现在原有的理论公式上加上一个修正因子,令其为δs, 则(18)式修正为
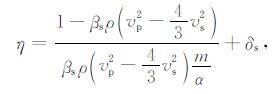
|
(20) |
令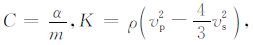
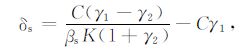
|
(21) |
其中γ1、γ2 可以根据具体的研究区的岩石物理测试或测井资料获得.
我们应用修正公式,重新计算了Ky2井的孔隙度.图 6c则为实测孔隙度与预测误差的交会图,经计算,该修正公式预测的孔隙度平均绝对误差仅为0.808%,比常规方法预测的精度提高了约3.3%,应用效果较好.
4 实际应用本文选取了海上的高精度三维地震资料进行叠前弹性反演,预测其孔隙度.由于目前各种叠前反演的软件[20]和叠前反演的方法[21-24]都比较成熟,通过较好的叠前三维地震资料可以较准确地反演出叠前的各种弹性参数.研究区的勘探目的层段为新近系珠江组地层,相带主要由开阔台地相、台地边缘相和台地前缘斜坡相组成.台地边缘礁、滩相储层岩性主要为藻灰岩、藻粘结灰岩,微晶或亮晶生屑灰岩、砂屑灰岩等.由于受到后期溶蚀作用的影响,孔隙类型主要为次生溶蚀孔隙和溶蚀缝.在地震剖面上礁相表现为丘形箱型、顶部强振幅、高连续、内部为波状、有时见前积结构等特征,滩相表现为席状透镜状、亚平行结构、中强振幅、中高连续、中低频等特征.但在实际地质沉积的过程中,一般是礁、滩互层发育,在地震剖面上一般很难把礁、滩完全地辨识出来,在储层物性上礁、滩差别也不大,因此把它们作为一类储层进行研究,统称为礁、滩相储层.
由于该研究区的礁、滩相储层具有一般生物礁滩储层典型的纵向、横向非均质强的特点,在利用常规方法进行储层孔隙度预测的时候效果并不理想.因此,本文根据研究区的礁、滩相储层的物性特征,提出了基于礁、滩相储层孔隙结构模型模拟的孔隙度预测方法.
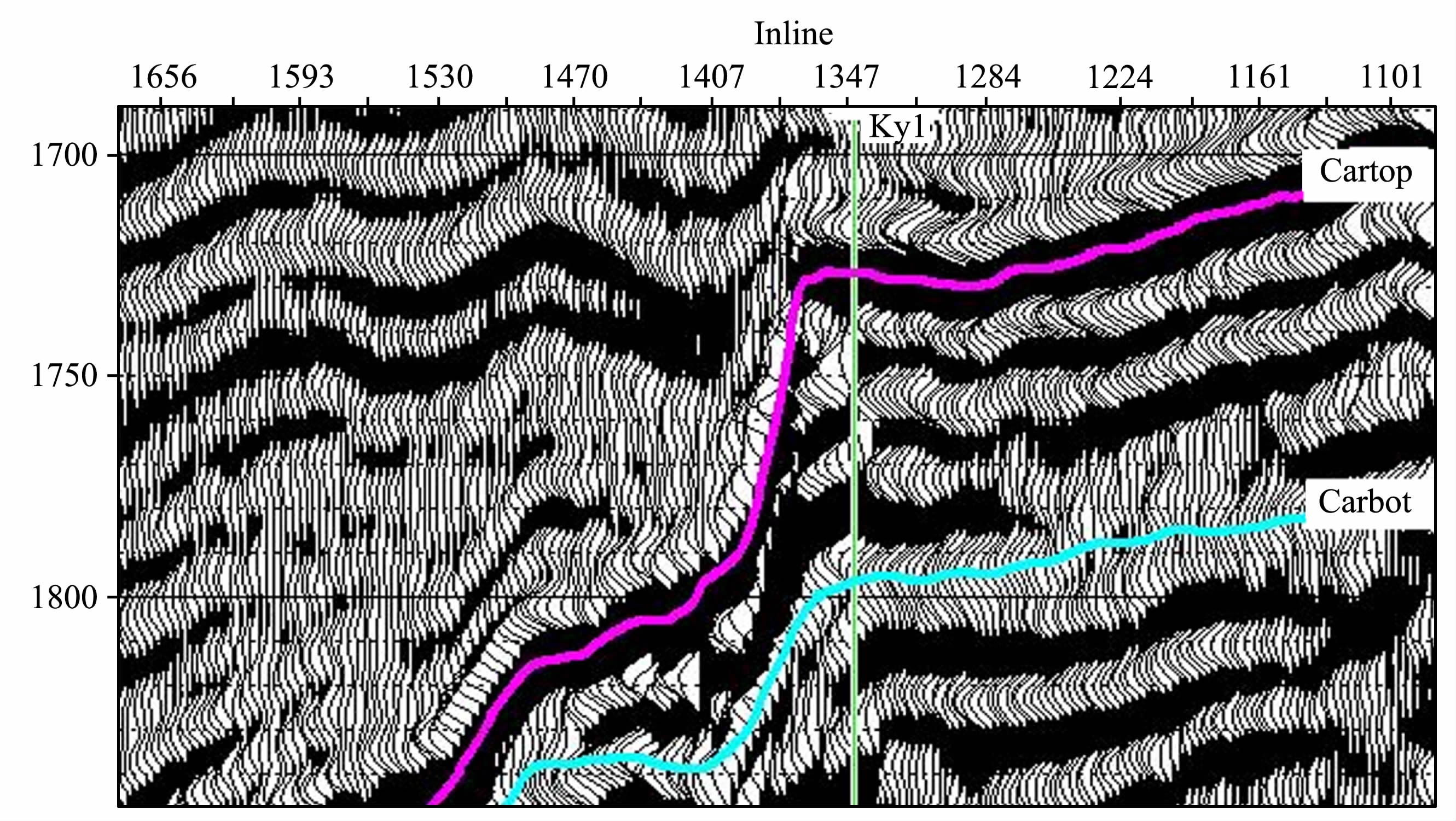
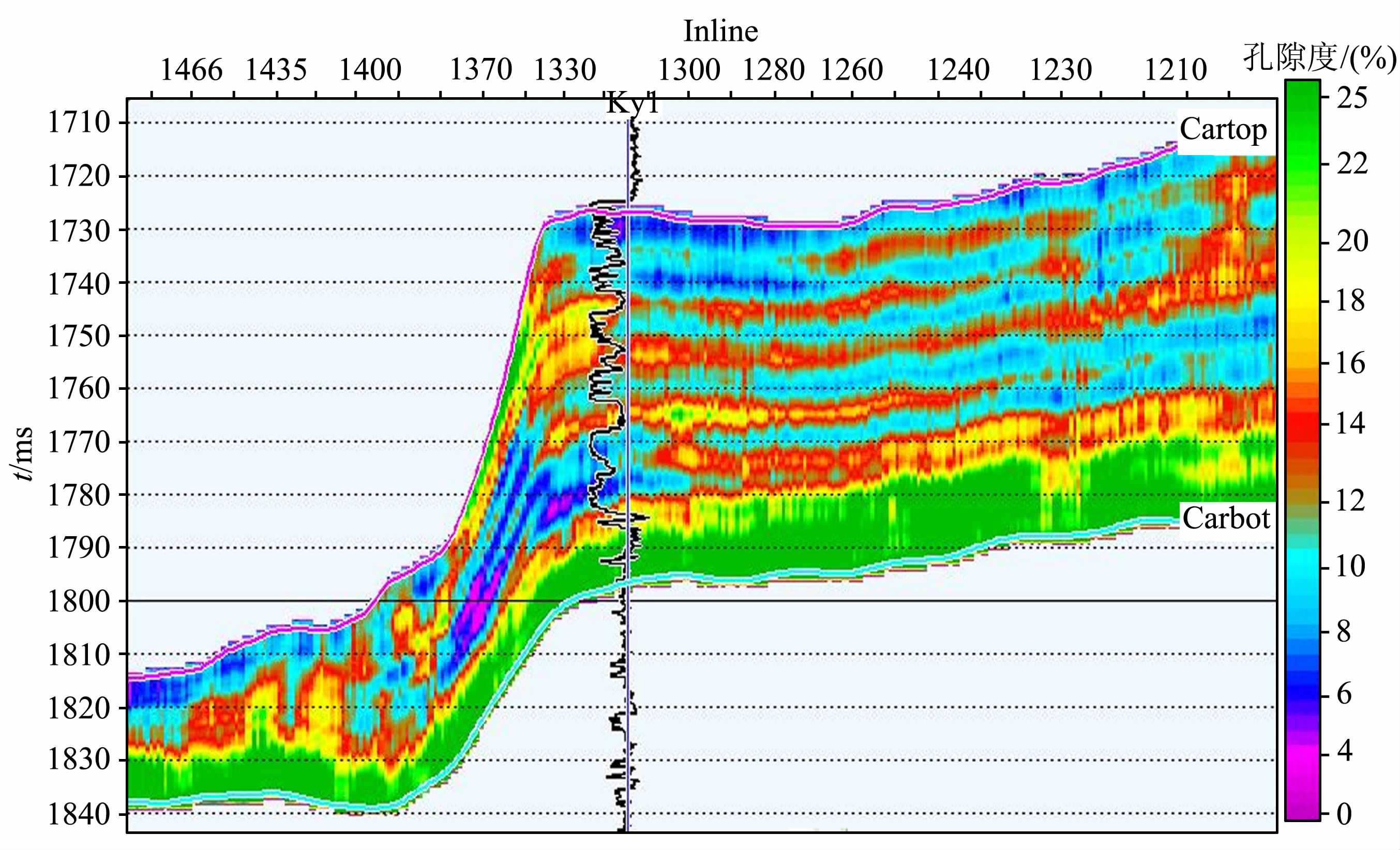
图 7为过Ky1井的原始地震剖面,从剖面上可以看出典型的礁、滩相储层的地震反射特征.图 8则为基于礁滩相储层孔隙结构模型模拟的孔隙度预测剖面,从过井的剖面图中实测孔隙度曲线与井旁道孔隙度预测的数据进行比较后可以发现,相关性非常高,预测的孔隙度数据的分布范围也与测井数据相当吻合,再从过井的剖面上也可以看出,孔隙度预测剖面的横向展布也基本符合地质规律.因此,从孔隙度预测的结果可以看出,基于礁滩相储层孔隙结构模型模拟的孔隙度预测方法在礁、滩相储层孔隙度预测中效果比较明显,能较好地提高孔隙度预测的精度.
|
图 7 过Ky1井的叠后原始地震剖面图 Fig. 7 The post-stack original seismic sectionnearby Ky1 well |
|
图 8 基于礁滩储层内部孔隙结构模拟的孔隙度预测剖面 Fig. 8 The prediction section of porosity based on simulation of internal pore structure model in reef-flat reservoir nearby Ky1 well |
本文从岩石物理的基本理论和岩石物理测试数据出发,在合理的假设前提下,运用Eshelby椭球包体裂缝理论和Gassman流体替换方程,推导和建立了孔隙度与饱和岩石(不排水)压缩系数、孔隙流体的压缩系数、岩石基质的压缩系数以及饱和岩石(排水)或干燥岩石压缩系数之间的关系式,合理和有效地模拟了非均质性较强的生物礁滩储层的孔隙结构.并在上述研究的基础上进行了实际应用.
根据上述理论研究和实际应用,得出以下结论:
(1) 生物礁滩储层孔隙结构模拟考虑了岩石二相体的基质、孔隙流体、孔隙形状以及岩石二相体的等效弹性参数对孔隙度的影响.在前人对干燥岩石、饱和岩石弹性参数的各方面研究的基础上,推导并建立了孔隙度与可以直接通过目前比较成熟的叠前反演技术得到的纵波速度、横波速度和密度,以及岩石二相体的基质、描述孔隙形状的纵横比之间的一个表达式.
(2) 通过岩石物理测试和测井分析证明了基于生物礁滩储层孔隙结构模拟的孔隙度预测方法的有效性和实用范围.即在同一地区得到的实验参数适合于岩性变化不大、孔隙结构相似的勘探目标区,当把实验参数用到另一勘探目标区时,需要对建立的公式进行修正(见公式(20)),修正因子因地区差异而不同.
(3) 由于孔隙形状对孔隙度的影响较大,在用该方法进行孔隙度预测时,应尽可能选用较多的、代表性较强的岩石薄片进行统计分析,确定研究区的岩石二相体的孔隙纵横比值.在确定岩石基质的压缩系数时,也应尽可能地多用岩石物理测试数据和测井数据进行反复调试,以获得较为准确的岩石基质压缩系数.
(4) 在下一步的研究工作中,希望通过以下两个方面来最大限度地发挥该方法的优势:第一,建立描述孔隙几何形状的孔隙纵横比和岩石基质压缩系数与已知有效弹性参数间的关系,消除孔隙几何形状和岩石基质压缩系数的影响,从而更加准确地预测其孔隙度的变化;第二,通过设计不同形状和孔隙纵横比的多孔介质模型进行理论测试与公式推导,从而建立更适合生物礁滩储层的孔隙几何形状的理论公式,对原有Eshelby公式进行修正和改进.
| [1] | 赵澄林, 朱筱敏. 沉积岩石学. 北京: 石油工业出版社, 2005 . Zhao C L, Zhu Y M. Sedimentary Petrology (in Chinese). Beijing: Petroleum Industry Press, 2005 . |
| [2] | 陈顒, 黄庭芳. 岩石物理学. 北京: 北京大学出版社, 2001 . Chen Y, Huang T F. Petrophysics (in Chinese). Beijing: Beijing University Press, 2001 . |
| [3] | 贺振华, 黄德济, 文晓涛. 裂缝油气藏地球物理预测. 北京: 科学出版社, 2007 . He Z H, Huang D J, Wen X T. Geophysics Prediction in Fractured Hydrocarbon Reservoir (in Chinese). Beijing: Science Press, 2007 . |
| [4] | 刘卫, 肖忠祥, 杨思玉, 等. 利用核磁共振(NMR)测井资料评价储层孔隙结构方法的对比研究. 石油地球物理勘探 , 2009, 44(6): 773–778. Liu W, Xiao Z X, Yang S Y, et al. Comparative studies on methods of evaluation of reservoir pore structure by using NMR (nuclear magnetic resonance) well logging data. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 2009, 44(6): 773-778. |
| [5] | Liu Z H, Zhou C C, Liu G Q, et al. An innovative method to evaluate formation pore structure using NMR logging data. SPWLA 48th Annual Logging Symposium , 2007, paper S. |
| [6] | 肖亮. 利用核磁共振测井资料评价储集层孔隙结构的讨论. 新疆石油地质 , 2008, 29(2): 260–263. Xiao L. Application of NMR log data to formation pore structure evaluation. Xinjiang Petroleum Geology (in Chinese) (in Chinese) , 2008, 29(2): 260-263. |
| [7] | 蒲秀刚, 黄志龙, 周建生, 等. 孔隙结构对碎屑岩储集岩物性控制作用的定量描述. 西安石油大学学报(自然科学版) , 2006, 21(2): 15–25. Pu X G, Huang Z L, Zhou J S, et al. Quantitative characterization of the controlling effect of pore structure on the physical property of clastic reservoir. Journal of Xi'an Shiyou University (Natural Science Edition) (in Chinese) (in Chinese) , 2006, 21(2): 15-25. |
| [8] | 代金友, 张伟, 熊琦华, 等. 成岩作用对储集层物性贡献比率研究. 石油勘探与开发 , 2003, 30(4): 54–58. Dai J Y, Zhang W, Xiong Q H, et al. Effects of diagenesis on reservoir property and auality, a case study of the Cainan Oilfield in east of Zhun Ga'er Basin. Petroleum Exploration and Development (in Chinese) (in Chinese) , 2003, 30(4): 54-58. |
| [9] | Niu B H, Sun C Y, Yan G Y, et al. Linear numerical calculation method for obtaining critical point, pore fluid, and framework parameters of gas-bearing media. Applied Geophysics , 2009, 6(4): 319-326. DOI:10.1007/s11770-009-0036-8 |
| [10] | Wyllie M R J, Gregory A R, Gardner G H F. An experimental investigation of factors affecting elastic wave velocities in porous media. Geophysics , 1958, 23: 459-493. DOI:10.1190/1.1438493 |
| [11] | Li M, Wu H L, Feng Q F, et al. Matrix porosity calculation in volcanic and dolomite reservoirs and its application. Applied Geophysics , 2009, 6(3): 287-298. DOI:10.1007/s11770-009-0030-1 |
| [12] | Nur A, Mavko G, Dvorkin J, et al. Critical porosity: a key to relating physical properties to porosity in rocks. The Leading Edge , 1998, 17: 357-362. DOI:10.1190/1.1437977 |
| [13] | 陈遵德, 祝文亮, 王卫华, 等. 孔隙度预测中的地震特征优化方法及应用. 石油学报 , 1999, 20(1): 50–55. Chen Z D, Zhu W L, Wang W H, et al. The method and application of seismic feature optimization in porosity prediction. Acta Petrolei Sinica (in Chinese) (in Chinese) , 1999, 20(1): 50-55. |
| [14] | Russel B H. The application of multivariate statistics and neural networks to the prediction of reservoir parameters using seismic attributes . Calgary: Department of Geology and Geophysics, Canada, 2004 |
| [15] | 吴媚, 符力耘, 李维新. 高分辨率非线性储层物性参数反演方法和应用. 地球物理学报 , 2008, 51(2): 546–557. Wu M, Fu L Y, Li W X. A high-resolution nonlinear inversion method of reservoir parameters and its application to oil/gas exploration. Chinese J| Geophys| (in Chinese) (in Chinese) , 2008, 51(2): 546-557. |
| [16] | 范铭涛, 沈全意, 吴辉, 等. 复杂岩性裂缝-孔隙型储层孔隙度计算方法研究. 天然气工业 , 2005, 25(5): 29–30. Fan M T, Shen Q Y, Wu H, et al. Porosity calculation method of complex lithological fractured-porous reservoir. Natural Gas Industry (in Chinese) (in Chinese) , 2005, 25(5): 29-30. |
| [17] | 金龙, 陈小宏, 姜香云. 利用地震资料定量反演孔隙度和饱和度的新方法. 石油学报 , 2006, 27(4): 63–66. Jin L, Chen X H, Jiang X Y. Simultaneous inversion of porosity and saturation using seismic data. Acta Petrolei Sinica (in Chinese) (in Chinese) , 2006, 27(4): 63-66. |
| [18] | 石玉梅, 姚逢昌, 孙虎生, 等. 地震密度反演及地层孔隙度估计. 地球物理学报 , 2010, 53(1): 197–204. Shi Y M, Yao F C, Sun H S, et al. Density inversion and porosity estimation. Chinese J| Geophys| (in Chinese) (in Chinese) , 2010, 53(1): 197-204. |
| [19] | Gary M, Tapan M, Jack D. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media. Cambridge: Cambridge University Press, 2003 . |
| [20] | 石磊, 王昌景. 常用的几种反演软件的比较. 西南石油学报 , 2004, 26(3): 16–19. Shi L, Wang C J. The comparison of several seismic inversion software. Journal of Southwest Petroleum Institute (in Chinese) (in Chinese) , 2004, 26(3): 16-19. |
| [21] | 杨培杰, 印兴耀. 非线性二次规划贝叶斯叠前反演. 地球物理学报 , 2008, 51(6): 1876–1882. Yang P J, Yin X Y. Non-linear quadratic programming Bayesian pre-stack inversion. Chinese J| Geophys| (in Chinese) (in Chinese) , 2008, 51(6): 1876-1882. |
| [22] | Hampson D P, Russell B H. Simultaneous inversion of pre-stack seismic data. SEG/ Houston 2005 Annual Meeting , 2005: 1633-1637. |
| [23] | Connolly P. Elastic impedance. The Leading Edge , 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [24] | 杨培杰, 印兴耀. 支持向量机叠前地震反演方法. 中国石油大学学报 , 2008, 32(1): 37–41. Yang P J, Yin X Y. Pre-stack seismic inversion method based on support vector machine. Journal of China University of Petroleum (in Chinese) (in Chinese) , 2008, 32(1): 37-41. |
 2011, Vol. 54
2011, Vol. 54