2. 海军海洋测绘研究所,天津 300061;
3. 信息工程大学测绘学院,郑州 450052
2. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China;
3. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450052, China
在地球物理领域,经常利用磁力勘探方法推断地球地质结构以及勘查油气与矿产资源分布状况[1];在开发利用海洋的过程中,水下磁性目标探测也是经常需要面对的问题[2, 3].根据磁性体磁场空间分布特征确定其对应的场源体几何与磁性参数,称为磁异常的反(演)问题[4].场源与磁异常场以及两者间的响应函数构成了反演的基本要素,不同性质场源体的响应函数也存在很大差异,且基本上都隶属非线性问题[5].针对磁性体相关参数求解问题,国内外提出了众多非线性问题解决方法,典型的方法有:解析信号法(也称全梯度模法)[6~8]、欧拉反褶积法[9~11]、神经网络法[12, 13]、遗传算法[14~16]等,其中,前两种方法在确定磁性体平面位置方面应用最为广泛,但在求解磁性体埋深及磁性参数时,还需借助其他解决方法以提高参数计算精度.
长期以来,最小二乘法在地球物理反演领域中发挥了十分重要的作用,有效地解决了一些线性或非线性问题.然而,如何将最小二乘法应用到磁性体参数反演中,目前仅在理论研究上进行了探索,尚无公开文献分析其具体应用结果情况.最小二乘法在磁场反演应用中未得到足够重视的主要原因是其收敛的不稳定性[17],影响收敛性的主要因素概括为三个方面:(1)响应函数的强非线性;(2)非线性方程组中待定参数过多;(3)含有角度参数.以最基本的球体磁场模型为例[18],设测区背景场为线性变化,测点P(x,y,z)处磁场总强度可用式(1)表示:
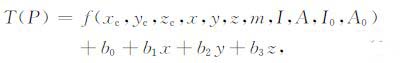
|
(1) |
式中,f(·)为球体磁异常响应函数,B=b0+b1x+b2y+b3z为测区背景场表达式,(xc,yc,zc)为球体中心位置,I、A和I0、A0 分别为磁化强度与地磁场方向倾角及偏角.
从式(1)中可以看到,当已知测点位置(x,y,z)和磁场总强度值T(P)时,共需求解12 个待定参数.由于待定参数过多,且包含四个角度参数,按常规的最小二乘法联立n(n>12)个非线性超定方程组求解时,极易造成法方程系数阵出现病态,并导致计算结果严重发散,从而制约了该方法在磁异常反演中的应用.为了减少待定参数维数,可以通过仪器测量或地磁场模型计算等方法获取测区I0 和A0 信息,同时忽略背景场因素B影响.然而,不论采用何种方法,获取的I0 和A0 都存在一定的偏差,这种偏差最终会传递给其他参数计算结果,偏差过大时,可能会增大计算结果的发散程度;在地磁场变化复杂或其他磁性体干扰场较大的情况下,忽略背景场影响往往导致计算结果精度较低,甚至出现错误的结果.
本文针对上述问题,将磁异常三分量作为观测值,采用最小二乘两步迭代法分步计算磁性体几何与磁性参数以及背景场参数.文中详细研究了该方法的基本原理和技术措施,通过实测资料检验了方法的可行性和有效性.
2 球体磁场解析表达式自然界中一些有限大小的三度磁性体,当其中心埋深大于磁性体走向长度2 至3 倍时,它们在地表产生的磁场特征与球体磁场类似,因而将球体磁场模型作为研究对象同时具有理论意义和现实意义,国内外大多数磁性体定位方面研究成果[19, 20]也是基于该磁场模型,本文的研究同样采用该磁场模型.
在笛卡尔坐标系中,球体在测点P(x,y,z)处的感应磁异常矢量形式为:
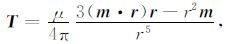
|
(2) |
式中,T=Txi+Tyj+Tzk为磁性体引起的矢量磁异常(单位为“T”),m=mxi+myj+mzk为矢量磁矩(单位为“A·m2”),r=rxi+ryj+rzk= (x-xc)i+ (y-yc)j+ (z-zc)k为磁性体中心(xc,yc,zc)至测点P间矢径(单位为“m”),μ 为磁导率(单位为“Tm/A”),在磁力勘探或水下磁性目标探测中,通常认为空气或水等非磁性介质中的磁导率与真空磁导率μ0 相同[21],即空气或水中的磁导率为μ0=4π×10-7Tm/A[22].
T用矩阵形式表示为:
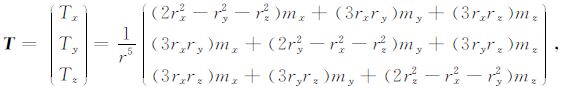
|
(3) |
式中,为简化符号运算,忽略了因子μ0/4π,以下均用黑体形式表示列向量.
定义位置函数矩阵R为:
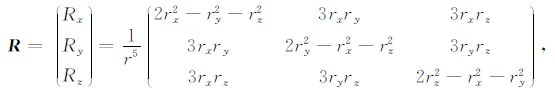
|
(4) |
则(3)式可简记为:
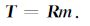
|
(5) |
在三分量磁场测量中直接获取的是测区磁场分量,其中包含探测对象的磁异常,同时也含有地磁场和其他磁性体干扰异常影响(称其联合影响为“背景场").尽管相关文献提出了一些磁异常提取方法,但提取后的磁异常场中或多或少都包含部分背景场影响[23].而在总场测量方式中,通过空域或频域手段换算的磁异常也存在部分趋势背景场.设测区共计N个测点,观测值为探测对象磁异常和背景场之和,则所有测点观测值形成的向量为:

|
(6) |
其中,Bi = (Bix Biy Biz) T 为第i个(i= 1,2,…,N)测点处磁异常分量所包含的背景场.
理论和实践应用中背景场模型应根据测区的实际情况进行适当选取.考虑到小尺度磁性体探测时所测量的区域范围较小,且地磁背景场空间上变化十分平缓,本文借鉴文献[24, 25]中给出的背景场处理方案,将测区背景场视为线性变化.此时,与观测值矩阵对应的位置函数矩阵为
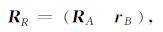
|
(7) |
其中,RA为(4)式定义的各测点磁异常位置函数矩阵,即
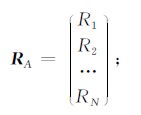
|
rB为背景场位置函数矩阵,即
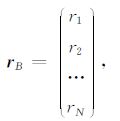
|
当观测数据呈三维分布时,

|
当观测面位于同一水平面时,
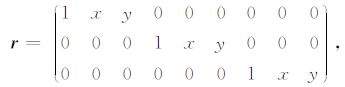
|
如果测区范围较大,也可将背景场位置函数矩阵进行中心化处理,用rx和ry分别代替x与y.
不失一般性,设磁场数据位于同一水平面,列立观测值误差方程为
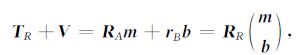
|
(8) |
式中,V为误差向量,
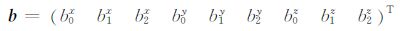
|
为三分量背景场系数,右上标为对应磁异常分量,右下标含义同式(1)中对应参数.
当给定磁性体初始中心位置
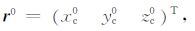
|
利用(7)式计算出位置函数矩阵RR,由于观测值TR与参数$\left( \begin{matrix} m \\ b \\ \end{matrix} \right)$之间是线性关系,根据最小二乘原理,参数$\left( \begin{matrix} m \\ b \\ \end{matrix} \right)$的估计值$\left( \begin{matrix} {\hat{m}} \\ {\hat{b}} \\ \end{matrix} \right)$应满足ψ =VTPV= min(这里P取单位阵),由函数自由极值求解方法,可得

|
(9) |
解算出参数( $\hat{m}$T $\hat{b}$T)T 后,将其作为已知参数重新代入(8)式进一步求解磁性体中心位置参数.可以看到,由(8)式建立的方程组中观测值TR与待定参数xc、yc 及zc 是非线性关系.下面利用最小二乘法求解位置参数.
根据最小二乘原理,参数估计值$\hat{x}$c、$\hat{y}$c 和$\hat{z}$c 同样应使ψ = min,即

|
(10) |
式中,Tiv(v=x,y,z)为磁场分量观测值;Φv($\hat{x}$c,$\hat{y}$c,$\hat{z}$c;μi)(v=x,y,z)为磁异常与背景场联合影响分量理论表达式;μi= (xi,yi,zi).
采用Taylor公式将Φ 在(xc0,yc0,zc0)处展开,并忽略高次项得:
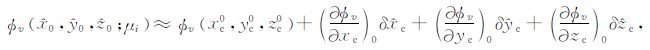
|
(11) |
式中,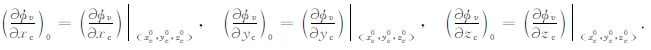
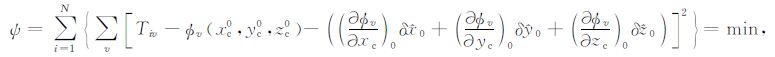
|
(12) |
式中,v=x,y,
再次根据函数自由极值求解方法,得待定参数修正值为:
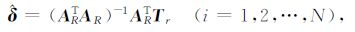
|
(13) |
式中,$\hat{\delta }$= (δ$\hat{x}$0 δ$\hat{y}$0 δ$\hat{z}$0 ) T 为磁性体中心位置参数初始值的修正值;
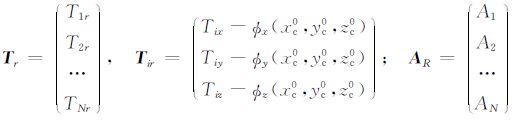
|
为Jacobi矩阵,
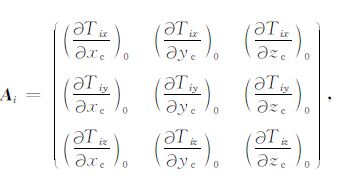
|
Ai中各元素表达式为
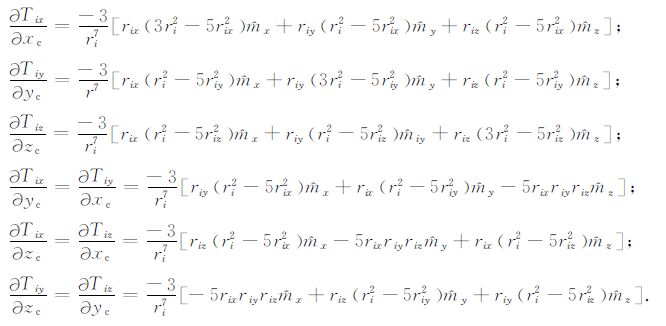
|
则经过修正后的磁性体中心位置为:
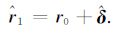
|
(14) |
由(14)式计算的结果即为经过修正后的磁性体中心位置.这里需要指出的是,经(11)式线性化后是Φv近似式,因为它略去了$\hat{\delta }$ 二次以上的项,当$\hat{\delta }$ 很小时,略去高次项对计算精度影响较小.如果因为某种原因不能求得较为准确的参数近似值,即$\hat{\delta }$ 很大时,将造成参数值之间存在较大不符值.这时应将(14)式位置计算结果作为位置参数初始值,利用(9)式计算磁矩和背景场参数,将计算结果作为已知值,结合(13)式进一步求解位置参数修正值,如此反复迭代计算,直至满足终止迭代准则.本文在实例计算中采取的终止迭代准则为:max|δ| <ε,即各修正值绝对值的最大值小于ε.
以上即为单个磁性体的数据处理方法和步骤,其流程可用如图 1 所示的框架图表示,当初始信息为磁异常分量数据时,则可以省略虚线框中的步骤.
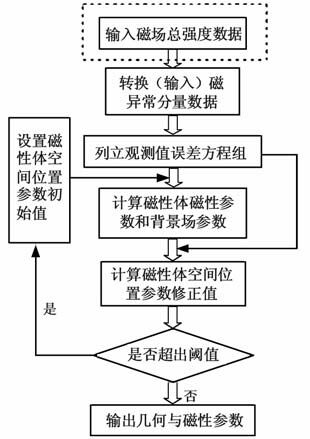
|
图 1 最小二乘两步迭代法数据处理流程框架图 Fig. 1 Data processing flow diagram of two-step iterative least square approach |
本文给出的是利用磁异常三分量数据求解磁性体几何与磁性参数的方法,实际计算中也可用单分量或双分量数据求解磁性体参数,其求解思路与上述采用三分量数据解算方法大致相同,只需将观测方程中的观测值替换为单分量或双分量观测数据,并将其中的三维矩阵转变成二维或一维矩阵即可,限于篇幅限制,这里不再赘述.为增强提出方法的适用性,进一步给出多个磁性体参数的计算方法.设磁性体数目为K,仿照(8)式,观测值误差方程矩阵形式为:
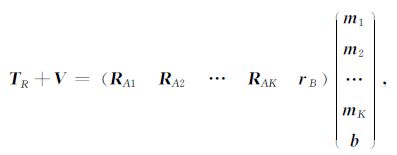
|
(15) |
式中,RA、rB、m和b对应(8)式中各符号含义.
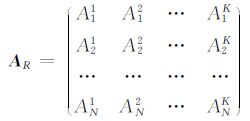
给定各磁性体中心位置初始值,则可按(9)式的求解方法计算出参数$\hat{m}$1 $\hat{m}$2 … $\hat{m}$K( $\hat{b}$),再仿照(13)式求解初始值修正值,此时的Jacobi矩阵
|
Apq中q为磁性体序号,p为测点序号.如果修正值满足终止迭代准则,则修正后的参数值即为各磁性体中心位置;否则,应反复迭代,直到满足终止迭代准则.
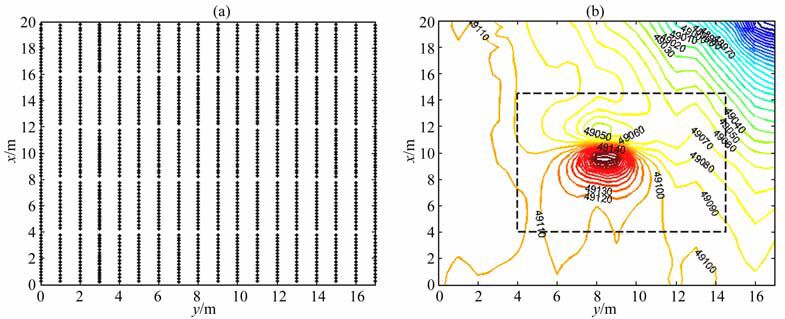
4 实例计算与分析1997年9月德国在汉堡采用磁探测方法对二战遗留炸弹进行了探测,探测仪器为G-858 铯光泵总场测量磁力仪,灵敏度为0.01nT.如图 2a所示为探测某英制GP500炸弹(下文称为“探测目标")所在区域测点与测线平面分布情况,测区面积约17m×20m,对应的磁场总强度分布如图 2b所示,探测目标质量为226.5kg,其实际中心位置为(10m,8.5m,2m).下面采用提出的最小二乘两步迭代方法计算探测目标位置,为尽量减少其他磁性目标干扰异常影响,以提高定位精度,选取图 2b中虚线框内D={(x,y)狘4m≤x≤14.5m,4m≤y≤14.5m}磁探测数据参与计算.
|
图 2 测区测点分布和磁场总强度等值线图 (a)测区测点分布图;(b)测区磁场总强度等值线图(等值线上的数字单位为nT,等值线间隔10nT). F Fig. 2 Survey point distribution and contour map of total field (contour interval 10 nT) (a) Survey point distribution; (b) Contour map of total field. |
经各项数据处理后D域内磁场最大值为49249.87nT,最小值为49030.77nT,平均值为49096.52nT.由于提出的方法是基于磁异常分量,故采用文献[26]中给出的方法换算磁异常三分量.由图 2a可以看出,y方向测线间隔分布较为规则,为1m左右;而x方向测点间距差异较大,平均在0.25m左右.分量换算方法是基于规则网格化磁场数据,因此,首先采用Kriging法对测区磁场进行格网化处理,格网化后磁场数据分辨率为0.5 m×0.5m;其次,用IGRF模型计算该测区当时地磁倾角和偏角分别为68.30°与-0.1°.经分量换算后,D域内磁异常分量Tx、Ty和Tz等值线如图 3所示.
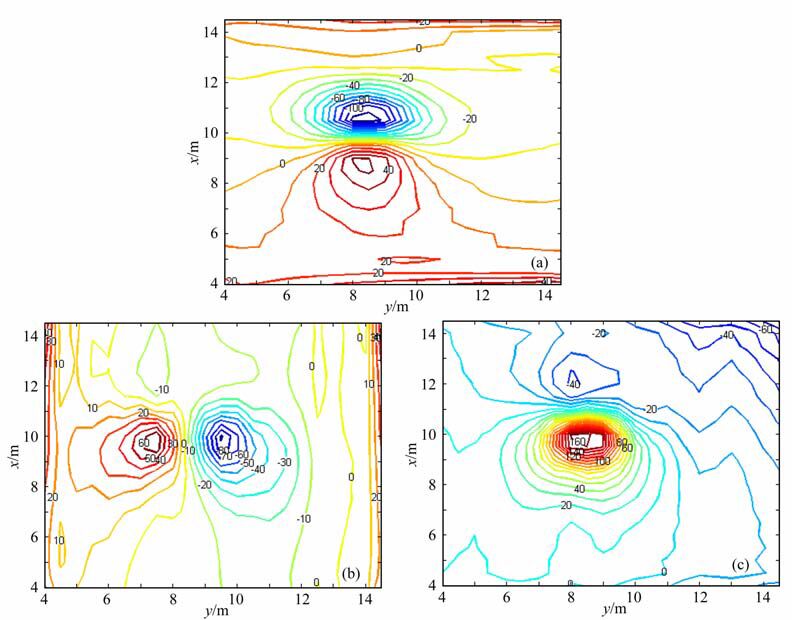
|
图 3 实测数据磁场总强度T换算得到的Tx(a)、Ty(b)和Tz(c)等值线图(等值线上的数字单位为nT,等值线间隔10nT) Fig. 3 Contour maps of Tx(a),Ty (b) and Tz (c) components calculated from total field datum (contour interval 10nT) |
从磁场分布来看,D域内磁异常主要由单一磁性目标引起,且磁场特征以及换算后磁异常分量特征与球体对应磁异常特征都极为相似,验证了一定条件下可将三度体磁场当作球体磁场来处理的结论.为比较目标初始位置参数对迭代收敛速度的影响,选取的目标初始位置参数与真值在三坐标轴方向之差的绝对值均为5m,即xc =5m、yc =3.5m、zc=7m,以 max{|υk-υk-1|}<ε =0.01m(v=x,y,z)作为终止判断准则.经迭代计算,满足终止判断准则的迭代次数为102 次,各次参数迭代计算结果三维分布如图 4a所示,图 4b所示为点位误差随迭代次数变化规律.
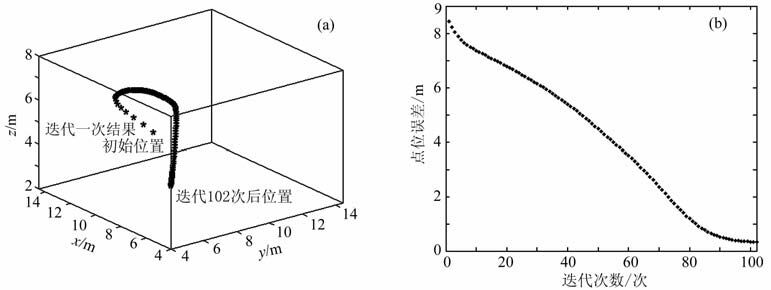
|
图 4 探测目标中心空间位置迭代结果三维分布图及点位误差图 (a)中心位置参数计算结果三维分布图;(b)点位误差随迭代次数变化关系. Fig. 4 3-D distribution of center location's iterative results and its error chart (a) 3-D distribution of center location; (b) Position error with the iterative times. |
从图 4可以看出,随着迭代次数不断增加,参数计算结果越来越逼近探测目标体中心位置,且迭代90次之前的参数收敛速度明显高于之后的收敛速度,90 次之后点位误差逐渐趋于稳定,其中σ90 =0.520m,σ102=0.324 m.为检验终止判断准则中ε=0.01m的合理性,本文还以ε=0.001 m 和ε=0.0001m分别计算了各自迭代次数和最终点位误差.取ε=0.001 m 时,迭代次数为120 次,σ120 =0.293m;取ε=0.0001 m 时,迭代次数为137 次,σ137=0.291m.可见,当ε=0.01m 减小1至2个数量级时,最终结果相差不大,说明采用本文的判断准则是合理的.
参数计算统计结果与迭代次数关系如表 1 所示,为观察初始阶段参数迭代计算结果的变化规律,同时限于篇幅,表 1中详细列出了前10次迭代计算结果和迭代10次后部分计算结果.
|
|
表 1 迭代次数与参数计算结果统计 Table 1 Result statistic of calculated parameters with iterative times |
尽管点位误差随迭代次数接近线性减小,但由表 1可以看到,$\hat{x}$c 、$\hat{y}$c 和$\hat{z}$c 收敛速度存在较大差异,如前8次迭代$\hat{x}$c 收敛速度最快,$\hat{y}$c 收敛速度次之,$\hat{z}$c 收敛速度最慢;随后$\hat{y}$c 收敛速度超越$\hat{x}$c ,在55次迭代之前基本保持线性收敛,经过55 次迭代后,$\hat{x}$c 和$\hat{y}$c 基本趋于稳定.在整个收敛过程中,$\hat{z}$c收敛速度始终最慢.经过102次迭代计算后,探测目标x、y和z方向坐标误差分别为0.246m、0.114m和0.177m,具有很高的位置计算精度.本文进一步比较了最小二乘迭代法和文献[24, 25]提出的欧拉反褶积法计算结果精度,欧拉反褶积法计算结果分别为$\hat{x}$c =10.228m、$\hat{y}$c = 8.497m、$\hat{z}$c =6.373m,虽然在平面位置上较本文方法精度略有提高,但其深度计算结果却存在非常大的误差.
另外,本文还通过大量仿真试验,表明利用最小二乘两步迭代法计算的结果都是收敛的,且参数计算精度主要与ε选择有关,当ε取很小时,最终计算结果差异较小;当ε固定时,迭代次数主要与参数初始值选取有关,初始值越接近探测目标中心位置,迭代次数越少;反之,初始值远离探测目标中心位置时,迭代次数将会增加.如将实例计算中探测目标初始位置选择xc0 =9、yc0 =9、zc0 =1时,且令ε=0.01m,迭代次数仅需18 次就可达到与上述102 次迭代相近的计算结果.因此,在设置初始值时,应充分结合磁性体磁场平面分布特征及所在测区自然地理情况等先验信息大致判断磁性体中心的位置.
5 结 论(1) 简要分析了常规最小二乘法在求解磁性体参数时产生发散解的原因,提出用磁异常三分量代替总强度磁异常作为观测值,以排除地磁场方向的相关角度参数影响,降低了未知参数的维数;并根据磁矩和磁化强度方向之间关系,用矢量磁矩代替磁化强度的磁倾角和磁偏角作为待定参数,从而彻底消除了反演模型中的角度参数,极大程度上减弱了解的病态性问题;
(2) 根据观测值和磁矩间线性关系,提出了最小二乘两步迭代法,该方法仅需要设置3 个中心位置参数初始值,先由中心位置初始参数计算出位置函数矩阵,采用线性最小二乘法求解磁矩参数;再将磁矩参数作为已知值,再次利用最小二乘法对初始位置参数进行修正,如此反复迭代计算,直至最终结果满足精度要求;
(3) 针对地磁场变化复杂或其他磁性体干扰磁场较大等情况,迭代计算过程中考虑了背景场的影响,将地磁场和其他磁性目标干扰异常联合影响视为线性变化,给出了相应的数据处理方法;此外,本文给出了多磁性体参数计算模型.实测数据验证表明:利用最小二乘两步迭代法计算出的结果是收敛的,具有很高几何与磁性参数计算精度,且受噪声影响较小;
(4) 对于相同的终止迭代准则,迭代次数主要与目标中心位置的初始值选取有关,设置的初始位置越接近磁性体中心,迭代次数越少.通过与目前应用最为广泛的欧拉反褶积法计算结果进行比较,基于磁性球体模型的深度计算结果精度要优于欧拉反褶积法,此外,本文方法还可以计算出磁性体磁矩,为判断磁性体类型提供了参考依据,显示提出的方法具有较强的适用性.
致谢感谢Geometrics公司为本文研究提供的磁探测实验数据.在本文的研究和撰写过程中,海军海洋测绘研究所黄谟涛教授和欧阳永忠高工给予了很多建设性的建议,特此感谢.另外,衷心感谢三位匿名评审专家提出的宝贵修改意见.
| [1] | 杨文采, 余长青. 根据地球物理资料分析大别—苏鲁超高压变质带演化的运动学和动力学. 地球物理学报 , 2001, 44(3): 346–359. Yang W C, Yu C Q. Kinematics and dynamics of development of the Dabie-Sulu UHPM Terrain on geophysical evidences. Chinese J.Geophys (in Chinese) , 2001, 44(3): 346-359. |
| [2] | Salem A, Hamada T, Asahina T H, Ushijima K. Detection of unexploded ordnance (UXO) using marine magnetic gradiometer data. Exploration Geophysics , 2005, 58: 97-103. |
| [3] | Tontini F C, Carmisciano C, Ciminale M, et al. High-resolution marine magnetic surveys for searching underwater cultural resources. Annals of Geophysics , 2006, 49: 1167-1175. |
| [4] | 姚姚. 地球物理反演基本理论与应用方法. 武汉: 中国地质大学出版社, 2002 . Yao Y. Basic Theory and Application of Geophysical Inverse Problems (in Chinese). Wuhan: China University of Geosciences Press, 2002 . |
| [5] | Vasco D W. Regularization and trade-off associated with nonlinear geophysical inverse problems: penalty homotopies. Inverse Problems , 1998, 14: 1033-1052. DOI:10.1088/0266-5611/14/4/018 |
| [6] | Roest W, Verhoef J, Pilkington M. Magnetic interpretation using the 3-D analytic signal. Geophysics , 1992, 57: 116-125. DOI:10.1190/1.1443174 |
| [7] | Hsu S K, Coppens D, Shyu C T. Depth to magnetic source using the generalized analytic signal. Geophysics , 1998, 63: 1947-1957. DOI:10.1190/1.1444488 |
| [8] | Salem A, Ravat D, Gamey J. Analytic signal approach and its applicability in environmental magnetic investigations. Journal of Applied Geophysics , 2002, 49: 231-244. DOI:10.1016/S0926-9851(02)00125-8 |
| [9] | Hsu S K. Imaging magnetic sources using Euler's equation. Geophysical Prospecting , 2002, 50: 15-25. DOI:10.1046/j.1365-2478.2001.00282.x |
| [10] | Nasreddine B, Armand G, Mohamed H, Haydar B. Interpretation of the aeromagnetic map of Eastern Hoggar(Algeria) using the Euler deconvolution, analytic signal and local wave number methods. Journal of African Earth Sciences , 2003, 37: 191-205. DOI:10.1016/j.jafrearsci.2002.12.001 |
| [11] | Geralda D F, Reid A, McInerney P. New discrimination techniques for Euler deconvolution. Computers & Geosciences , 2004, 30: 461-469. |
| [12] | Salem A, Ushijima K, Gamey T J, et al. Automatic detection of from airborne magnetic data using a neural network. Subsurface Sensing Technologies and Applications , 2001, 2: 191-213. DOI:10.1023/A:1011918119491 |
| [13] | 管志宁, 侯俊胜, 黄临平, 等. 重磁异常反演的拟BP神经网络方法及其应用. 地球物理学报 , 1998, 41(2): 242–251. Guan Z N, Hou J S, Huang L P, et al. Inversion of gravity and magnetic anomalies using pseduo-BP neural network method and its application. Chinese J.Geophys (in Chinese) , 1998, 41(2): 242-251. |
| [14] | Boschetti F, Dentith M C, List R D. Inversion of potential field data by Genetic Algorithms. Geophysical Prospecting , 1997, 45: 461-478. DOI:10.1046/j.1365-2478.1997.3430267.x |
| [15] | Boschetti F, Dentith M, List R. Inversion of potential field data by genetic algorithms. Geophysical Prospecting , 1997, 45: 461-478. DOI:10.1046/j.1365-2478.1997.3430267.x |
| [16] | 姚长利, 郝天珧, 管志宁, 等. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报 , 2003, 46(2): 252–258. Yao C L, Hao T Y, Guan Z N, et al. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms. Chinese J.Geophys (in Chinese) , 2003, 46(2): 252-258. |
| [17] | Abdelrahman E M, Sharafeldin S M. An iterative least-squares approach to depth determination from residual magnetic anomalies due to thin dikes. Journal of Applied Geophysics , 1996, 34: 213-220. DOI:10.1016/0926-9851(95)00017-8 |
| [18] | Daniela G, Marcos J, Arau'zo-Bravob, et al. Determination of the parameters of compact ferro-metallic objects with transforms of magnitude magnetic anomalies. Journal of Applied Geophysics , 2004, 55: 173-186. DOI:10.1016/j.jappgeo.2003.10.001 |
| [19] | Sun K, O'Neill K, Shubitidze F, et al. Fast data-derived fundamental spheroidal excitation models with application to UXO discrimination. Transactions on Evolutionary Computation , 2005, 43: 2573-2583. |
| [20] | Ginzburg B, Frumkis L, Kaplan B Z. An efficient method for processing scalar magnetic gradiometer signals. Sensors and Actuators , 2004, 114: 73-79. DOI:10.1016/j.sna.2004.03.008 |
| [21] | 管志宁. 地磁场与磁力勘探. 北京: 地质出版社, 2005 . Guan Z N. Geomagnetic Field and Magnetic Exploration (in Chinese). Beijing: Geological Publishing House, 2005 . |
| [22] | Wiegert R F. Magnetic anomaly sensing system for detection, localization and classification of magnetic objects. US Patent, US6841994B1 , 2005. |
| [23] | Ojo S B, Kangkolo R. Shortcomings in the determination of regional fields by polynomial fitting: A simple solution. Journal of Applied Geophysics , 1997, 36: 205-212. DOI:10.1016/S0926-9851(96)00043-2 |
| [24] | Stavrev P Y. Euler deconvolution using differential similarity transformations of gravity or magnetic anomalies. Geophysical Prospecting , 1997, 45: 207-246. DOI:10.1046/j.1365-2478.1997.00331.x |
| [25] | Daniela G, Marcos J, Arauzo B. Automatic interpretation of magnetic data based on Euler deconvolution with unprescribed structural index. Computers & Geosciences , 2003, 29: 949-960. |
| [26] | Blakely R J. Potential Theory in Gravity and Magnetic Applications. Cambridge: Cambridge University Press, 1995 . |
 2011, Vol. 54
2011, Vol. 54


