2. 清华大学数学科学系, 北京 100084
2. Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China
Biot流动和喷射流动是含流体多孔隙介质中流体流动的两种重要力学机制.1956年,Biot建立了描述多孔隙介质中波传播的Biot理论[1].这是孔隙介质研究的里程碑性事件,具有重大意义.然而,在很多情况下Biot理论预测的能量耗散和速度频散要比实际的能量耗散和速度频散低,不能合理解释许多实验结果和实际数据.1993 年,Dvorkin和Nur[2]基于各向同性情况提出了一种同时考虑了Biot流动和喷射流动力学机制的BISQ(Biot-Squirt)模型,通过对BISQ 模型预测结果、Biot模型预测结果和实验数据的比较,得出“BISQ 模型的预测结果比Biot理论的预测结果更准确"这一重要结论.之后,Parra[3]将BISQ 理论推广到横向各向同性双相介质情况.杨顶辉等[4]基于固-流耦合各向异性的思想,建立了高维一般含流体多孔隙各向异性介质中的BISQ 模型.另外,基于微观流场固-流相对运动速度的各向异性,杨顶辉和张中杰[5]研究了Biot流动和喷射流动耦合作用对弹性波衰减和频散的影响.国内其他学者也对BISQ 模型进行了大量深入研究:陈远峰等[6]将各向同性的BISQ 模型推广到黏弹性情况,聂建新等[7~10]研究了含流体非饱和多孔隙介质中的BISQ 模型、广义低孔渗介质中的BISQ 模型及其储层参数反演等问题.王克协等[11]应用BISQ 模型深入研究了孔隙介质中的慢P波的传播性质.
然而,上述研究都是针对各种情况首先给出模型,然后通过假设BISQ 模型的平面波解来研究各种波的频散和衰减性质.而直接通过波场模拟来研究BISQ 模型所揭示的含流体多孔隙介质中各种波传播规律的工作相对较少.2002 年,杨宽德等[12]基于BISQ 模型使用FCT 有限差分方法模拟了Biot流动和喷射流动作用下的波传播.然而,他们所使用的数值方法是只有二阶精度的中心差分方法,其波场模拟结果的精度相对较低,王者江[13, 14]研究了基于BISQ 机制的三维正交介质中弹性波的正演模拟及其传播特征.本文中,我们将使用精度较高的FCT 紧致差分方法来求解BISQ 方程,研究含流体多孔隙介质中Biot流动和喷射流动共同作用下波传播规律.
本文的目的是利用紧致差分方法[15, 16]求解BISQ 方程,通过波场模拟研究复杂储层介质中在Biot流动和喷射流动耦合作用下各种波的传播规律.之所以选择紧致差分方法,是因为紧致差分方法使用xi附近的几个网格点上的加权平均来近似xi附近几个网格点处偏导数的加权平均.这样的处理使得紧致差分方法可以更好地消除数值频散[17, 18].在研究中我们也发现,由于双相BISQ 模型非常复杂,以至于高阶紧致差分方法虽然在一定程度上能减弱数值频散,但很难完全消除数值频散和源噪声.因此,本文同时应用通量校正传输(FCT)技术[19]来进一步消除数值频散和源噪声.数值实验表明,这种FCT 紧致差分算法能够有效压制波场数值频散和源噪声,得到清晰的波场快照和地震合成记录.从这些波场快照和地震记录中,我们得到BISQ 模型中的波频散和衰减规律,获得了和理论分析一致的结果.
2 BISQ 模型在时间-空间域内,杨顶辉等[4]基于固-流耦合各向异性的思想,导出了多孔隙各向异性介质中同时包含Biot流动和喷射流动力学机制的弹性波传播方程,这组方程在二维横向各向同性孔隙介质情况下可简化成由以下7 个方程构成的偏微分方程组:
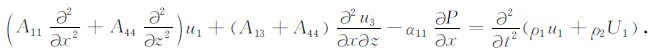
|
(1) |
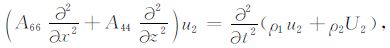
|
(2) |

|
(3) |
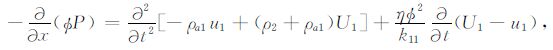
|
(4) |

|
(5) |
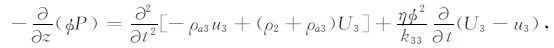
|
(6) |

|
(7) |
其中,ρ1 = (1-Φ)ρs,ρ2 =Φρf.
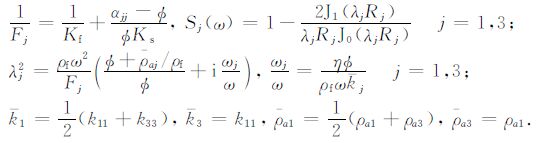
|
ui和Ui(i=1,2,3)分别表示固体和流体在x、y和z方向上的位移分量,Φ 为孔隙度,ρs 和ρf 分别为固体和流体密度,ρai(i=1,3)为第i方向固-流耦合附加质量密度,ρ1 表示单位体积内固体质量,ρ2 表示单位体积内液体质量,η为流体黏滞系数,P为流体压力,Ks 为固体骨架体积模量,流体体积模量Kf可由流体声速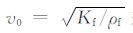

|
J0 和J1 分别为零阶和一阶贝塞尔函数,R1、R2(其中R1 =R2)、R3 分别为x、y、z三个方向的特征喷射流动长度,ω 为角频率.
3 紧致差分方法 3.1 紧致差分的基本原理设x∈ R,f(x)是充分光滑的函数,网格点为xi=ih,i=0,±1,±2,…,h是网格步长.构造插值函数
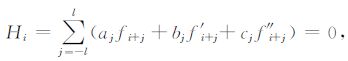
|
(8) |
其中,Hi表示以xi点为中心的差分格式,l表示此格式向左向右延伸的网格点数,aj,bj,cj是待定系数,fi,f′i,f″i分别表示xi点上的函数值f(xi)及其一阶导数值f′(xi)和二阶导数值f″(xi).下面介绍如何利用公式(8)获得函数在节点处的一阶导数和二阶导数插值近似公式.
3.1.1 一阶导数的紧致差分格式若令(8)式中l= 3,cj= 0(j= 0,±1,…,±l),bj=b-j(j=±1,…,±l),b0 =1,b3 =b-3 =0,aj=-a-j(j=±1,…,±l),a0 =0,则整理可得Lele[15]给出的关于fi一阶导数的紧致差分格式:
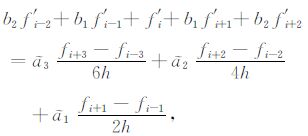
|
(9) |
其中系数$\tilde{a}$1,$\tilde{a}$2,$\tilde{a}$3,b1,b2 的计算方法如下:将(9)式中各项在xi=ih点处作Taylor展开,整理成关于h的多项式,并令关于h的低阶幂次的系数为零,即可得到关于$\tilde{a}$1,$\tilde{a}$2,$\tilde{a}$3,b1,b2 的方程组:

|
(10) |
求解方程组(10),即得$\tilde{a}$1 =1.4167,$\tilde{a}$2 =0.6733,$\tilde{a}$3 =0.01,b1 =0.5,b2 =0.05,此时(9)式就是7点10阶紧致差分格式[15].
3.1.2 二阶导数的紧致差分格式令(8)式中l=3,bj=0(j=0,±1,…,±l),cj=c-j(j=±1,…,±l),c0 =1,c3 =c-3 =0,aj=a-j(j=±1,…,±l),则整理可得Lele[15]给出的关于fi二阶导数的紧致差分格式:
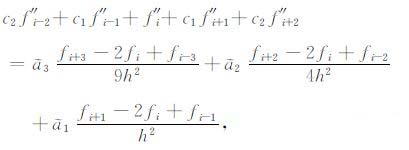
|
(11) |
与(9)式中系数的求解方法相似,通过求解方程组,求出$\tilde{a}$1 = 0.5923,$\tilde{a}$2 = 1.1546,$\tilde{a}$3 = 0.0439,c1 =0.3715,c2 =0.0239.这是一个7点10阶紧致差分格式.详细的推导过程可参阅文献[15, 18].
3.2 BISQ方程的紧致差分格式我们利用上述紧致差分格式的基本思想,实现求解多孔隙各向异性介质中同时包含Biot流动和喷射流动力学机制的BISQ方程组的紧致差分算法.
首先,用算子形式的紧致差分格式离散空间导数,将偏微分方程组(1)~(7)转化为关于时间t的常微分方程组后,用二阶中心差分方法解此关于时间的半离散化常微分方程组初值问题.为计算方便,把算子形式的格式简化为矩阵形式的格式.这里采用Vichnevetsky[16, 20]的算子记法.
设以等步长h剖分计算区域,时间步长为Δt,uxn(i,j)表示ux(ih,jh,nΔt),Uxn(i,j)表示Ux(ih,jh,nΔt),记
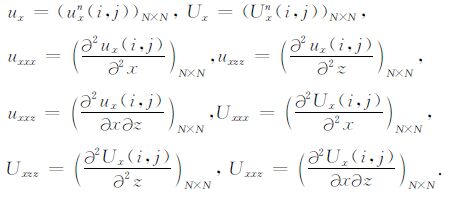
|
对于BISQ 模型中出现的微分算子
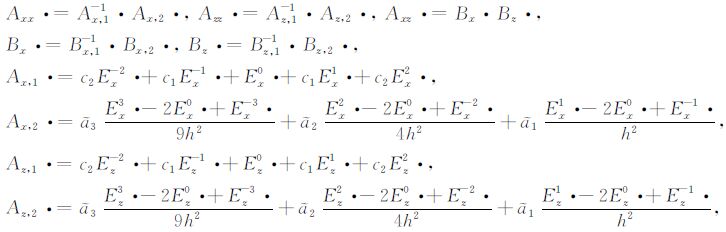
|
系数c2,c1,$\tilde{a}$1,$\tilde{a}$2,$\tilde{a}$3 是二阶紧致差分格式(11)中的系数.Exk·ui,jn=ui+kn,j,Ezk·ui,jn=ni,j+ku.同理可写出Bx,1·,Bx,2·,Bx·,Bz,1·,Bz,2·,Bz·,只是其系数是一阶紧致差分格式(9)中的对应系数.
用上述差分算子逼近(1)~ (6)式中的空间导数,用二阶中心差分离散时间导数得:
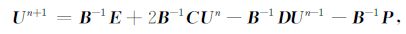
|
(12) |
其中,

|
为了考察FCT 处理技术[19]压制数值频散和源噪声的效果,我们第一个模型为均匀各向同性介质中的BISQ 模型.其介质参数分别为:固体密度ρs=2600kg/m3,流体密度ρf=1000kg/m3,质量耦合密度ρa=450kg/m3,流体声速v0=1500 m/s,孔隙度Φ=15%,流体黏滞系数η=4×10-7Pa·s,渗透率k=4×10-10m2,固体体积模量Ks=38GPa,固体弹性常数λ=9×109 kg/(m·s2),μ=10×109kg/(m·s2),其他计算参数选取为:x和z方向空间步长皆取为h=10m,时间步长Δt=6×10-4s,特征喷射流动长度R=1mm,角频率ω=4000Hz.
为叙述方便,我们称没有采用FCT 处理的紧致差分方法为基本的紧致差分方法,而称结合了FCT 处理技术的紧致差分方法为FCT 紧致差分方法.图 1给出了使用基本的紧致差分方法(图 1a)和FCT 紧致差分方法(图 1b)计算得到的固体位移x方向的分量ux在t=0.45s时刻的波场快照.

|
图 1 固体位移x方向分量ux在ux= 0.45 s时刻的波场快照 (a)使用基本的紧致差分方法;(b)使用FCT紧致差分方法. Fig. 1 The wave-field snapshots of the solid displacement component ux at t = 0.45 s generated by original compact different scheme (a) and the FCT compact different scheme (b) |
从图 1可以看到,如果不使用FCT 处理技术,波场快照中存在数值频散以及由震源离散所引起的源噪声.这些数值频散和源噪声的存在,使得图 1a所示的波场非常不清楚;而在FCT 紧致差分方法得到的波场快照中,由于引入了FCT 技术处理,所获得的波场变得非常清晰,没有任何可见的数值频散和源噪声(见图 1b).这说明FCT 处理技术可以有效地压制数值频散和源噪声.
4.2 模型2:BISQ模型和Biot模型的波场对比为考察使用BISQ 模型和Biot模型所得波场快照的差别,在这个数值算例中,我们选取孔隙度Φ=10%,流体黏滞系数η=1×10-9Pa·s,渗透率k=4×10-100m2,其他计算参数的选取与模型1中的散系数b=0.025 非常小,所以我们在波场快照中可以观测到慢P波.图 2a和图 2b分别给出了使用FCT 紧致差分方法求解Biot方程和BISQ 方程所得0.45s时刻的固体位移x分量的波场快照.

|
图 2 固体位移x方向分量^的波场快照 (a) Biot 模型;(b)BISQ 模型. Fig. 2 The wave-field snapshots of the solid displacement component at 1 = 0. 45 s based on the Biot model (a) and BISQ model (b) |
从图 2我们可以观测到快P波、S波和慢P波,整个波场非常清晰,这说明FCT 紧致差分方法能正确地模拟含流体多孔隙介质中的各种波动.另一方面,比较图 2a和2b,我们会发现,使用BISQ 模型计算得到的快P 波和慢P 波波速明显小于由Biot理论计算得到的快P波和慢P波波速,但是两者的S波波速无明显差异,这说明压缩波(快P 波和慢P 波)受喷射流影响较大,而剪切波受喷射流影响较小.这与Dvorkin 和Nur[2]的研究结果是一致的.
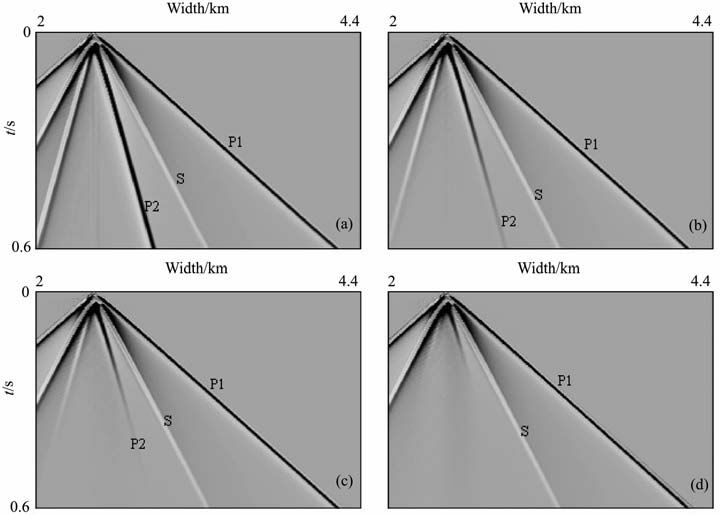
4.3 模型3:黏滞相界模型为了考察耗散系数b=ηΦ2/k对波场,尤其是对波场中慢P波的影响,我们计算了4种情况下的BISQ 模型的弹性波场和地震记录.其耗散系数分别为b=0,5.625,11.25,22.5,孔隙度Φ=15%.计算区域:0≤x≤4.4km,0≤z≤4.4km,震源放在计算区域的中心,随时间变化的震源函数为f(t)=(1-2π2f2t2 )e-π2f2t2 ,其他参数与模型1 中的参数一致.
图 3(a~h)分别对应于4种情况下T=0.27s和T=0.6s时刻的波场快照.图 3表明,4种不同情况下的弹性波场中都存在3种不同的波,它们在波场快照中由外到内依次为:快P波、S波和慢P波.每种波形的波前面都是以震源为中心的圆形,其各向同性特征十分明显.同时我们也可看到,随着耗散系数b的增大,慢P波的速度也随之增大,但是其能量衰减的速度也显著加快.另外,整个波场波形都非常清晰,无数值频散,这再次说明FCT 处理技术能够有效压制数值频散和源噪声.

|
图 3 不同耗散系数b和不同时刻T得到的模型3的固体位移ux分量的波场快照 (a)b=0,T=0.27;(b)b=0,T=0.6;(c)b=5.625,T=0.27;(d)b=5.625,T=0.6;(c)b=11.25,T=0.27;(f)b=11.25;T=0.6;(g)b=22.5,T=0.27;(h)b=22.5,T=0.6. Fig. 3 The wave-field snapshots of the solid displacement component component u, in the model 3 at dissipation coefficient b and different time T |
为了更清晰地考察慢P波的衰减规律,图 4给出了这4种情况下的地震记录.检波器埋藏深度和震源深度一致.从人工合成地震记录可以得到,当耗散系数b=0时,慢P波非常清楚,且能量很强,没有能量衰减,这与无耗散方程所描述的慢P波传播规律一致;当b>0时,随着传播距离的增大和传播时间的增长,慢P波的振幅明显衰减,能量显著减弱;与无耗散情形所对应的地震记录图 4a相比,最大耗散系数b=22.5情况下的地震记录(图 4d)中的慢P波衰减更加显著;图 4d也表明,慢P波的振幅随偏移距的增大迅速衰减.这解释了为什么在实际观测中很难观测到慢P波,因为实际的含流体多孔隙介质具有很强的黏滞性,这意味着实际孔隙介质具有较大的耗散系数,这使得波场中的慢P波能量迅速衰减,并导致检波器很难接收到慢P波信号.
|
图 4 模型3中固体ux分量的合成地震记录 (a)b=0;(b)b=5. 625;(c)b=11. 25;(d)b= 22. 5. Fig. 4 The seismic records of the solid displacement component ux |
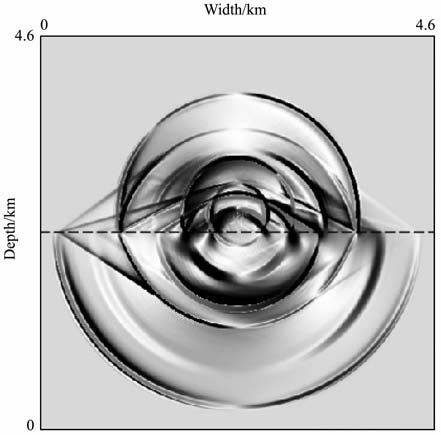
在实际油藏介质中,存在许多速度突变层.充分研究地震波在这些断层处的传播规律并加以应用,将极大地提高地震勘探水平.下面以简单的、含有水平断层的双层模型为例,研究BISQ 模型所描述的波在断层处的传播规律.
为此,设计如下双层模型:模型大小为4.6km×4.6km,震源放在(2.3km,2.1km)处.上层固体弹性参数为λ=6×109kg/(m·s2),μ=6×109kg/(m·s2),深度为2.3km;下层弹性参数为λ=24×109kg/(m·s2),μ=24×109kg/(m·s2),深度为2.3km.流体黏滞系数η=0,空间步长为Δx=Δz=10m,时间步长Δt=3×104s.震源函数及参数与模型1中的震源函数、其他参数对应一致.
图 5给出了含流体双层孔隙介质中波传播的波场快照.从快照中,我们可以看到波场中的波大致可以分为以下5类:(1)直达波类:包括直达快纵波P1、直达横波S和直达慢纵波P2等;(2)反射波类:包括快纵波P1的反射纵波P1P1、横波S的反射横波SS和慢纵波P2 的反射波P2P2 等;(3)透射波类:包括快纵波P1 的透射波P1p1、横波S 的透射波Ss和慢纵波P2 的透射波P2p2 等;(4)转化波类:包括快纵波P1在界面反射之后转化为P1S波和慢纵波P1P2,横波S 在界面反射之后转化为快纵波SP和慢纵波SP2,慢纵波在界面反射之后转化为快纵波P2P1和横波P2S,快纵波P1在界面透射之后转化为横波P1s和慢纵波P1p2,横波S 在界面透射之后转化为快纵波Sp1和慢纵波Sp2;(5)首波类:在图 5 可以观测到约10 种连接不同反射波和折射波的首波,这些首波在波场中表现为面波.同时,在波场中,我们可以清晰地观测到反射波能量随入射角变化而发生变化,即所谓的AVO现象.
|
图 5 双层BISQ模型固体位移分量〜的波场快照 Fig. 5 The wavefield snapshot of the solid displacemei |
可见双层孔隙介质中的波场信息非常丰富,同时也相当复杂.每一种直达波传经间断面后都将产生多种波,深入研究地震波在间断处的传播有助于充分地利用多波地震资料以加深对双相储层介质的认识,具有很重要的理论和实际意义.
5 结 论双相孔隙介质中的BISQ 模型综合考虑了Biot流动和喷射流动这两种最主要的孔隙介质中的流体流动形式.本文使用FCT 紧致差分方法模拟研究了双相孔隙介质中同时受Biot流动和喷射流动共同作用下的波的传播规律,并考察了耗散系数b对弹性波场中的慢P 波波速、能量耗散等波场特征的影响规律.
数值结果表明,Biot流动和喷射流动共同作用下的快P波传播速度比仅受Biot流动影响情况下的快P波传播速度慢,慢P波的衰减更快,说明具有局部特征的喷射流动对压缩波的衰减和频散具有重要作用;而对于剪切波,两种模型得到的剪切波速几乎一致,说明在各向同性情况下喷射流对剪切波的影响不明显.这一结果与波衰减和频散的理论分析结果[2,4]一致.
对于黏滞相界的孔隙介质,当耗散系数b较小时,从固相位移波场快照中可以清晰地观测到三种波:快P波、S波和慢P 波.并且当耗散系数b为0时,慢P波无衰减;随着耗散系数b增大,慢P波的衰减趋于明显;当耗散系数增大到一定程度之后,慢P波迅速衰减,在快照中已经很难观测到慢P波.这是慢P波在实际观测中很难被观测到的重要原因.
双层孔隙介质中每种波在断层处均发生反射、折射和转化,每种波都将产生多种波,从而使得含流体储层介质中的波场信息非常丰富,同时也相当复杂,深入研究地震波在断层处的传播规律,必将加深我们对油藏储层的认识,提高石油物探水平.
数值结果还表明,FCT 技术可以有效压制弹性波场中的数值频散和源噪声,我们可以利用FCT 紧致差分方法深入研究双相孔隙介质中的BISQ 模型波场中各种波的传播规律.
附 录 FCT 紧致差分算法这里给出FCT 紧致差分算法的计算流程.总的来说,FCT 紧致差分分为三步(紧致差分计算、漫射、反漫射校正),其具体步骤如下[19]:
Step1.给出初始值Ui,j0,利用第3节介绍的紧致差分算法计算Ui,jn+1;
Step2.漫射计算;
(1) 计算第n时间层内的漫射通量
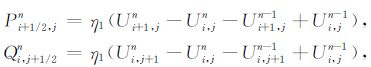
|
这里η1 是一个介于0和1之间的变量.数值算例表明FCT 技术压制数值频散的效果依赖于参数η1 的选择.η1 越大,数值频散压制的越好,但是这同时也会减弱波场内波形的振幅;随着η1 逐渐减小,波场内的波的振幅会逐渐恢复到真值,但是同时也会影响到FCT 压制数值频散的效果.Yang 等[19]指出,使用FCT 技术压制中心差分格式的数值频散时,0.008≤η1≤0.05是比较合适的.而我们的研究发现,对于FCT 结合紧致差分方法,η1=0.0025足以有效压制差分格式中产生的数值频散,这意味着我们计算得到的波场中的波振幅会更加接近于真实振幅.
(2) 为了能够压制数值频散,利用漫射通量平滑由紧致差分格式得到的解
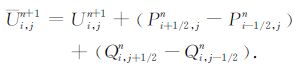
|
Step3.反漫射计算;
(1) 计算第n+1时间层的漫射通量
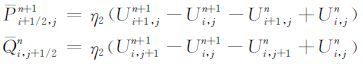
|
这里η2 的选取方式与η1 相同.在本文的计算中,选取η2=0.003.
(2) 计算反漫射通量

|
(3) 利用反漫射通量修正平滑解Un+1i,j,得到有效压制数值频散的最终解
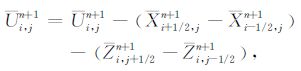
|
其中
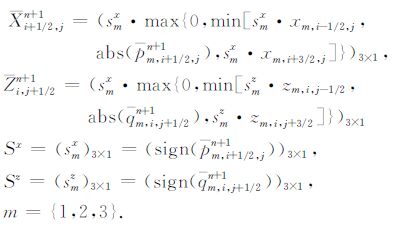
|
| [1] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, I. Low-frequency range, II. Higher frequency range. J. Acoust. Soc. Amer , 1956, 28: 168-191. DOI:10.1121/1.1908239 |
| [2] | Dvorkin J, Nur A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms. Geophysics , 1993, 58: 524-533. DOI:10.1190/1.1443435 |
| [3] | Parra J O. The transversely isotropic poroelastic wave equation including the Biot and the squirt mechanisms: Theory and application. Geophysics , 1997, 62: 309-318. DOI:10.1190/1.1444132 |
| [4] | Yang D H, Zhang Z J. Poroelastic wave equation including the Biot/Squirt mechanism and the solid/fluid coupling anisotropy. Wave Motion , 2002, 35(3): 223-245. DOI:10.1016/S0165-2125(01)00106-8 |
| [5] | Yang D H, Zhang Z J. Effects of the Biot and the squirt-flow coupling interaction on anisotropic elastic waves. Chinese Science Bulletin , 2000, 45(23): 2130-2138. DOI:10.1007/BF02886316 |
| [6] | Chen Y F, Yang D H, Yang H Z. Biot/squirt model in viscoelastic porous media. Chinese Physics Letters , 2002, 19(3): 445-448. DOI:10.1088/0256-307X/19/3/348 |
| [7] | Nie J X, Yang D H, Yang H Z. Wave dispersion and attenuation in partially saturated sandstones. Chinese Physics Letters , 2004, 21(3): 572-575. DOI:10.1088/0256-307X/21/3/044 |
| [8] | 聂建新, 杨顶辉, 杨慧珠. 基于非饱和多孔隙介质BISQ模型的储层参数反演. 地球物理学报 , 2004, 47(6): 1101–1105. Nie J X, Yang D H, Yang H Z. Inversion of reservoir parameters based on the BISQ model in partially saturated porous media. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1101-1105. |
| [9] | Nie J X, Yang D H, Yang H Z. A generalized viscoelastic Biot/squirt model for clay-bearing sandstones in a wide range of permeabilities. Applied Geophysics , 2008, 5(4): 249-260. DOI:10.1007/s11770-008-0038-y |
| [10] | 聂建新, 杨顶辉, 巴晶. 含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究. 地球物理学报 , 2010, 53(2): 385–392. Nie J X, Yang D H, Ba J. Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay. Chinese J. Geophys. (in Chinese) , 2010, 53(2): 385-392. |
| [11] | Cui Z W, Wang K X, Cao Z L, et al. Slow waves propagation in BISQ poroelastic model. Acta Physica Sinica , 2004, 53(9): 3083-3089. |
| [12] | 杨宽德, 杨顶辉, 王书强. 基于Biot-Squirt方程的波场模拟. 地球物理学报 , 2002, 45(6): 853–861. Yang K D, Yang D H, Wang S Q. Wavefield simulation based on the Biot/Squirt equation. Chinese J. Geophys. (in Chinese) , 2002, 45(6): 853-861. |
| [13] | 王者江. 基于BISQ机制的三维双相正交介质正演模拟及传播特性研究. 长春: 吉林大学, 2008 Wang Z J. A study of numerical simulation and propagation characteristics for 3D two-phase orthotropic medium based on the BISQ mechanism (in Chinese). Changchun: Jilin University, 2008 http://www.oalib.com/references/19467906 |
| [14] | Wang Z J, He Q D, Wang D L. The numerical simulation for a 3 D two-phase anisotropic medium based on BISQ model. Applied Geophysics , 2008, 5(1): 24-43. DOI:10.1007/s11770-008-0011-9 |
| [15] | Lele S K. Compact finite difference schemes with spectral-like resolution. Journal of Comput. Physics , 1992, 103: 16-42. DOI:10.1016/0021-9991(92)90324-R |
| [16] | Vichnevetsky R, Bowles J B. Fourier analysis of numerical approximations of hyperbolic equations. Philadelphia: SIAM , 1982. |
| [17] | 王书强, 杨顶辉, 杨宽德. 弹性波方程的紧致差分方法. 清华大学学报(自然科学版) , 2002, 42(8): 1128–1131. Wang S Q, Yang D H, Yang K D. Compact finite difference scheme for elastic equations. J. Tsinghua Univ. (Science and Technology) (in Chinese) , 2002, 42(8): 1128-1131. |
| [18] | 王书强. 弹性波方程的紧致差分方法及其波场模拟. 北京:清华大学数学科学系 , 2002. Wang S Q. The compact finite difference scheme of elastic equations and its numerical simulations (in Chinese). Beijing: Department of Mathematical Sciences, Tsinghua University (in Chinese) , 2002. |
| [19] | Yang D H, Liu E R, Zhang Z J, et al. Finite-difference modelling in two-dimensional anisotropic media using a flux-corrected transport technique. Geophys. J. Int. , 2002, 148(2): 320-328. |
| [20] | Vichnevetsky R. Stability charts in the numerical approximation of partial differential equations: A review. Math. Comput. Simulation , 1979, 21(2): 170-177. DOI:10.1016/0378-4754(79)90130-7 |
 2011, Vol. 54
2011, Vol. 54


