2. 96165部队,江西乐平 333300;
3. 中科院大气物理研究所大气科学与地球物理流体动力学数值模拟国家重点实验室,北京 100029
2. No. 96165 Troops of PLA, Leping Jiangxi 333300,China;
3. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029,China
Rossby波是地球大气中的一种重要波动,在数值预报和气候预测中占有重要地位,以往对Rossby波研究多着眼于波动的稳定性问题,其研究方法也多用标准模法[1],关于这方面最早的工作是Charney[2]、Eady[3]和Kuo[4]提出的斜压和正压不稳定理论.尽管标准模方法有其自身的优点[5],但其只能研究扰动的线性发展,无法讨论初始场的影响和波动在发展中的形态演变[6-8].而实际大气中天气的发生发展,特别是一些灾害性天气都发生在有限时间内,这主要是由有限时段内急剧增长的扰动引起,因此研究和讨论有限时段内扰动的发展问题,对于从动力学的角度分析灾害性天气现象,以便做出准确预报是十分必要的.
作为初值问题,Orr[9]最早研究了平面无黏Couette流,指出能量在有限时段内存在快速增长的现象.Rosen[10]得到了Couette流的一般形式的解析表达式,并对能量的增长进行了研究.Farrell[11]采用Green函数法求出了特殊初值情形下的Couette流流函数的解析表达式,发现Couette流能量在开始一段时间内是快速增长的,达到最大值后随着时间又出现迅速衰减现象,当时间趋向无穷时,能量趋向于零.Boyd[12]应用多尺度展开法研究了线性与非线性方程的解指出,非线性方程存在孤立波解.Zeng[13, 14]和卢佩生等[15]研究过正压和斜压大气中Rossby波的演变.Farrell[16, 17]研究了阻尼斜压扰动的快速增长、中性Rossby波和斜压大气的最优激发机制.近年来,Farrell等[18, 19]进一步讨论了层结流体扰动发展问题.张亮等[20]在Tung[21]研究的基础上进一步得到了线性基流情形下的线性Rossby 波解析解,并讨论了初始场和环境场对Rossby波流场结构和能量演变的影响.
对于真实基流切变下Rossby 波的演变问题,Geisler等[22]研究了斜压大气Rossby波的稳定性,Hoskins等[23]研究了Rossby 波流场结构的演变,但没有分析总能量的演变.Redekopp 等[24]利用耦合的KdV 方程组研究了不同基流下Rossby 孤立波的演变,Zhang等[25]利用数值方法研究了斜压大气Rossby波总能量在三种特殊的非线性基流情形下的演变,发现对于不同的基流,总能量的演变是不一样的,但这些研究都没有考虑真实大气的情况.在真实大气中Rossby 波的运动方式是非线性的,纬向风随纬度的变化也是非线性的,这使得问题具有复杂性,给解析求解带来了困难,所以数值计算方法就成为了研究该问题的有效方法.
将Rossby波的演变问题作为初值问题来研究时,由于基流和方程都是非线性的,其解对初值应该是敏感的,那么初始波动上若有微小的扰动,其解随时间的演变会发生怎样的变化?这是我们关心的问题,对这个问题的讨论将对改进数值预报的质量有重要的意义.
本文针对准地转正压位涡方程,设计了一个高精度的隐式差分迭代公式,利用双Gauss函数拟合了500hPa高度上纬向风随纬度变化函数.在此基础上,数值计算了北半球中纬度地区Rossby 波流场结构和总能量随时间的演变,并讨论了初值对波动演变的影响.
2 数学模型及真实基流的拟合在只考虑西风基流U(y)的条件下,描写大气Rossby波的准地转正压位涡方程为

|
(1) |
其中ψ 为流函数,Δψ 为涡度,F、β、ε为非负常数.当ε=0时,(1)为线性方程;当ε=1时,(1)为非线性方程.在区域Ω = [0,Lx]×[0,Ly]中(1)式的初边值条件为
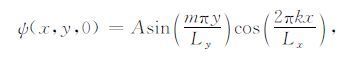
|
(2) |
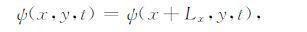
|
(3) |
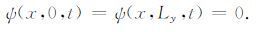
|
(4) |
(3)和(4)式表示x方向取周期边界条件,y方向取固壁边界条件.定义Rossby 波的总能量和相对总能量如下:
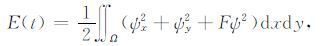
|
(5) |
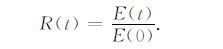
|
(6) |
对方程(1)空间采用差分方法离散化,时间积分采用Gauss-Seidel迭代法,求出Rossby波流函数的数值解后,再利用梯形积分公式按(5)和(6)式计算出总能量和相对总能量.
计算中时间和空间步长满足Δx= Δy和Δt=0.05Δx,每一时间层的最大迭代误差为eps=10-4,积分时间长度为60 天,空间、时间和速度的特征尺度分别为106 m、105 s 和10 m/s.流体平均厚度为5500m, A=1.0,β 和F取北纬45°处的值.
真实基流利用ECMWF2.5°×2.5°的500hPa再分析资料(1957-2002年)计算得到,首先计算各月纬向风的气候态,然后计算纬向平均得到只随纬度变化的纬向风气候场,最后将其作为基本气流用双Gauss函数进行数据拟合,求出真实基流的函数表达式.
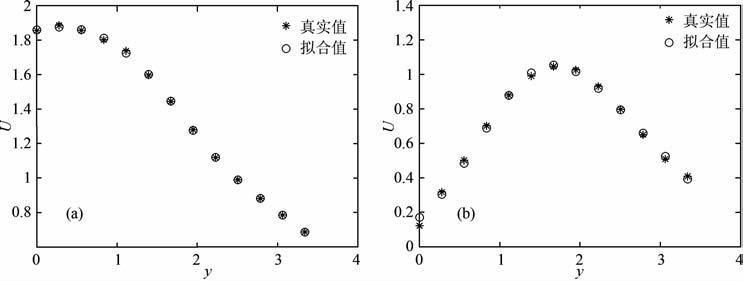
图 1给出了1、7月份的真实基流风速与拟合基流风速(图中横坐标表示经向的无量纲长度y,纵坐标表示无量纲的基流速度U).由图可看出,拟合值与真值非常接近,这说明利用双Gauss函数可以很好地模拟出基流风速随纬度的变化.
|
图 1 1月(a)和7月(b)500hPa上基流风速真实值与拟合值 Fig. 1 The real and fitted wind speeds of basic flow on 500hPa in Jan (a)and Jul(b) |
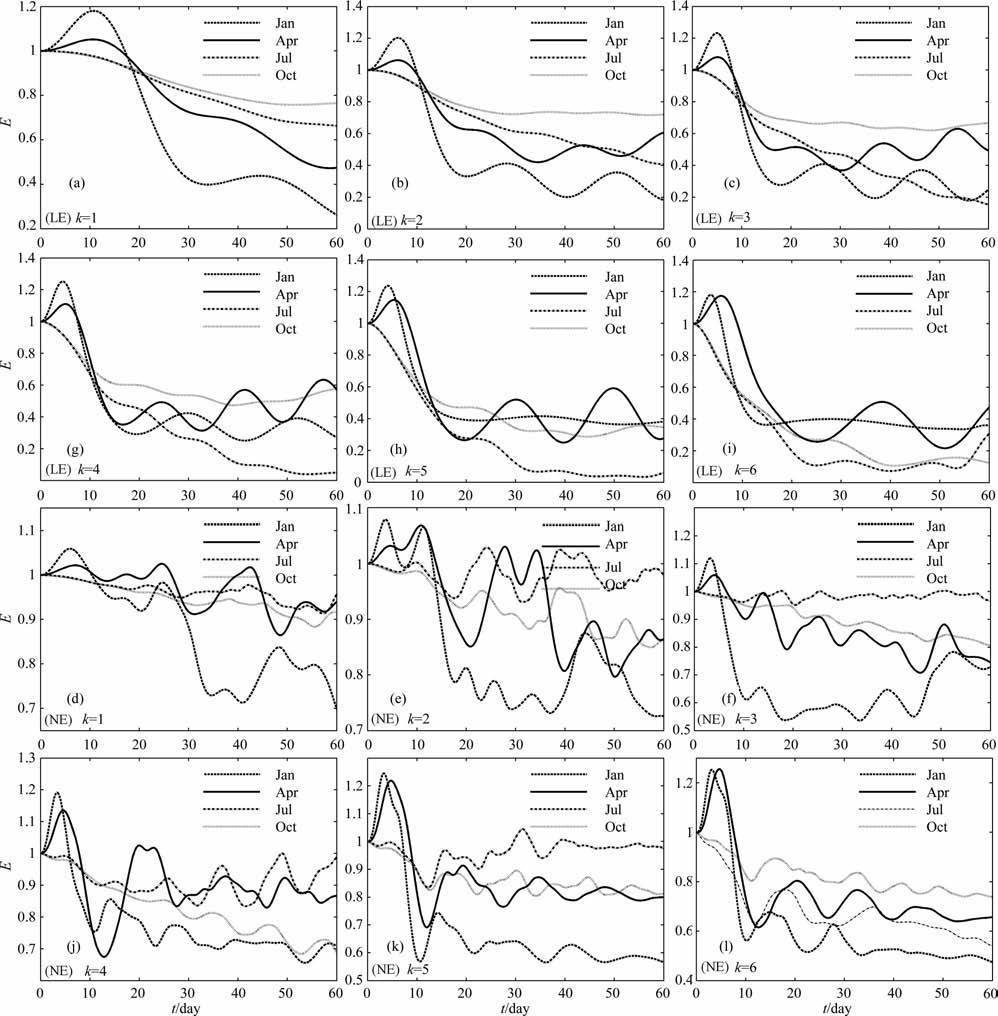
图 2分别给出了1、4、7和10月基流情形下,经向波数m=2和纬向波数k为1-6时,线性(LE)和非线性(NE)Rossby 波相对总能量E随时间t的演变.
|
图 2 m=2和不同纬向波数时,LE 与NE 随时间的演变(E为Rossby波相对总能量) Fig. 2 The evolutions of LE and NE with time when m=2and different latitudinal wave number |
分析图 2可看出,在真实的非线性基流情形下,线性和非线性Rossby波的相对总能量随时间的演变特征与线性基流的情形不同,在线性基流时,如果线性波动相对总能量在有限时段内增长,那么相对能量随时间的演变过程一定是先严格单调递增,达到最大值后再严格单调递减,且随着时间趋向于无穷,相对总能量趋向于零[16].
而非线性基流时,无论线性还是非线性波动相对能量随时间的演变都出现振荡型增长或振荡型衰减现象.二者的差异主要表现在振荡变化的周期和振幅上,非线性波动相对能量演变过程中的振荡周期更短,线性波动的振荡周期一般为20-30 天,非线性波动的振荡周期一般为15-20 天.一般而言,如果波动相对总能量在有限时段内增长,那么其最大值是线性波动大于非线性波动的;如果在有限时段内衰减,也依然.这表明,非线性不仅能够抑制能量的快速增长也抑制其快速衰减.
在相同的基流情形下,不同的初始场(k值不同)对线性和非线性波动相对总能量能否在有限时段内增长有很大的影响.对于纬向波数为1-3的超长波,当初始场在经向上为半个波(m=1)时(图略),不论是线性波动还是非线性波动,相对总能量在春夏季(4、7 月份)能快速增长达到极大值,特别是在春季达到的极大值最大,在秋冬季(10、1月份)增长很小.当初始场在经向上为1 个波(m=2)时(图 2),无论是线性波动还是非线性波动,相对总能量在春冬季(1、4 月份)能快速增长达到极大值,特别是在冬季达到的极大值最大,在夏秋季(7、10月份)变化都很小.
对于纬向波数为4-6的长波,当初始场在经向上为半个波(m=1)时(图略),不论是线性波动还是非线性波动,相对总能量也是在春夏季(4、7 月份)能快速增长达到极大值,但在夏季达到的极大值最大;在秋冬季(10、1 月份)都是先衰减然后振荡增长,但能量始终小于初始能量,并且它在冬季的衰减速度要明显快于其他三个季节.当初始场在经向上为1个波(m=2)时(图 2),无论是线性波动还是非线性波动,相对总能量在春冬季(1、4 月份)达到极大值较大,夏秋季(7、10月份)变化相对较小.
值得注意的是经向波数对线性和非线性波动能量的演变影响较大,随着经向波数的增大,线性与非线性波动能量随时间的演变特征差异更大.故波动能量能否增长不仅与基流有关,还与波动的初始结构有关,当二者达到最佳配合时,能量能在有限时段内增长,这时的波动活动对天气系统的发展最有意义.
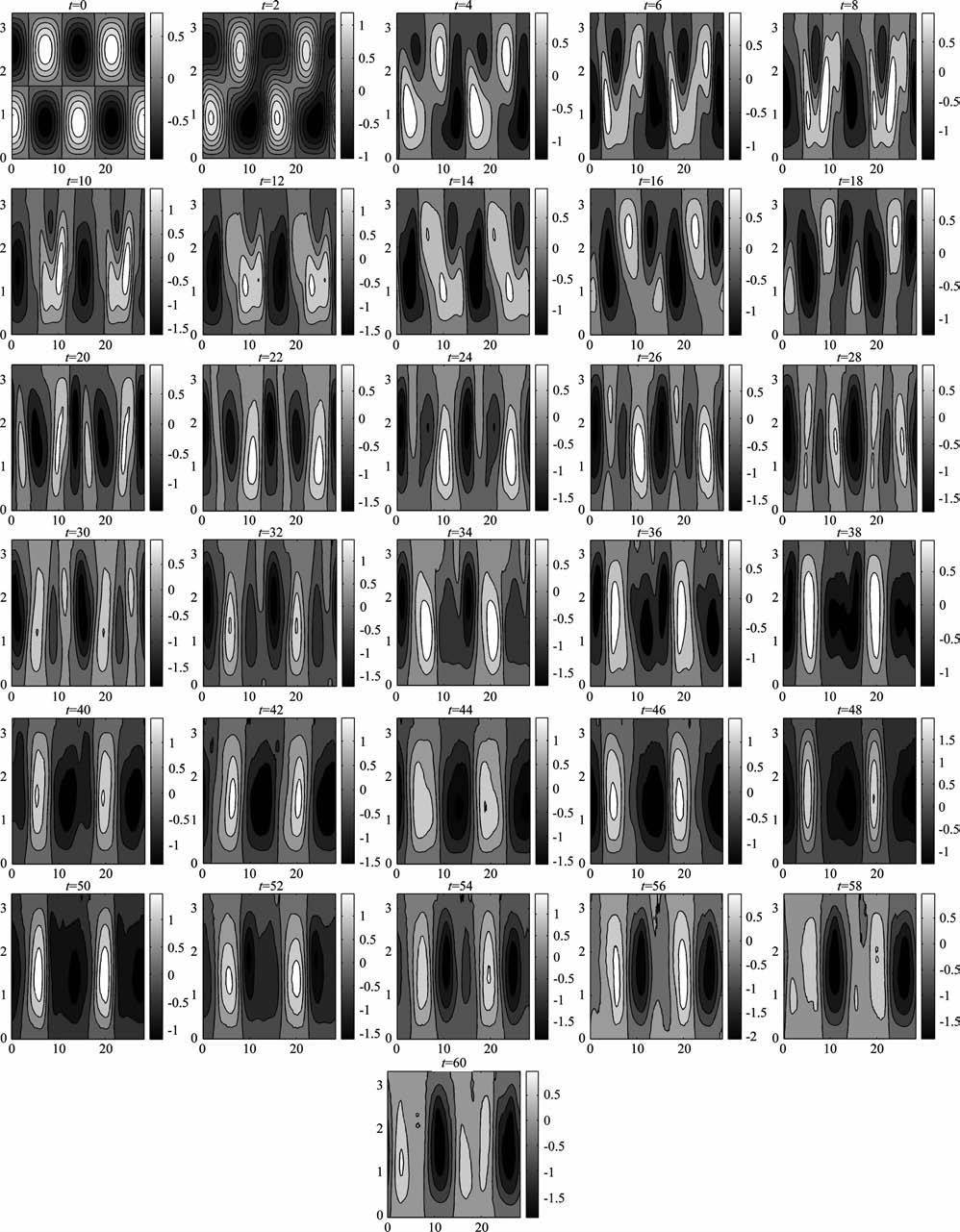
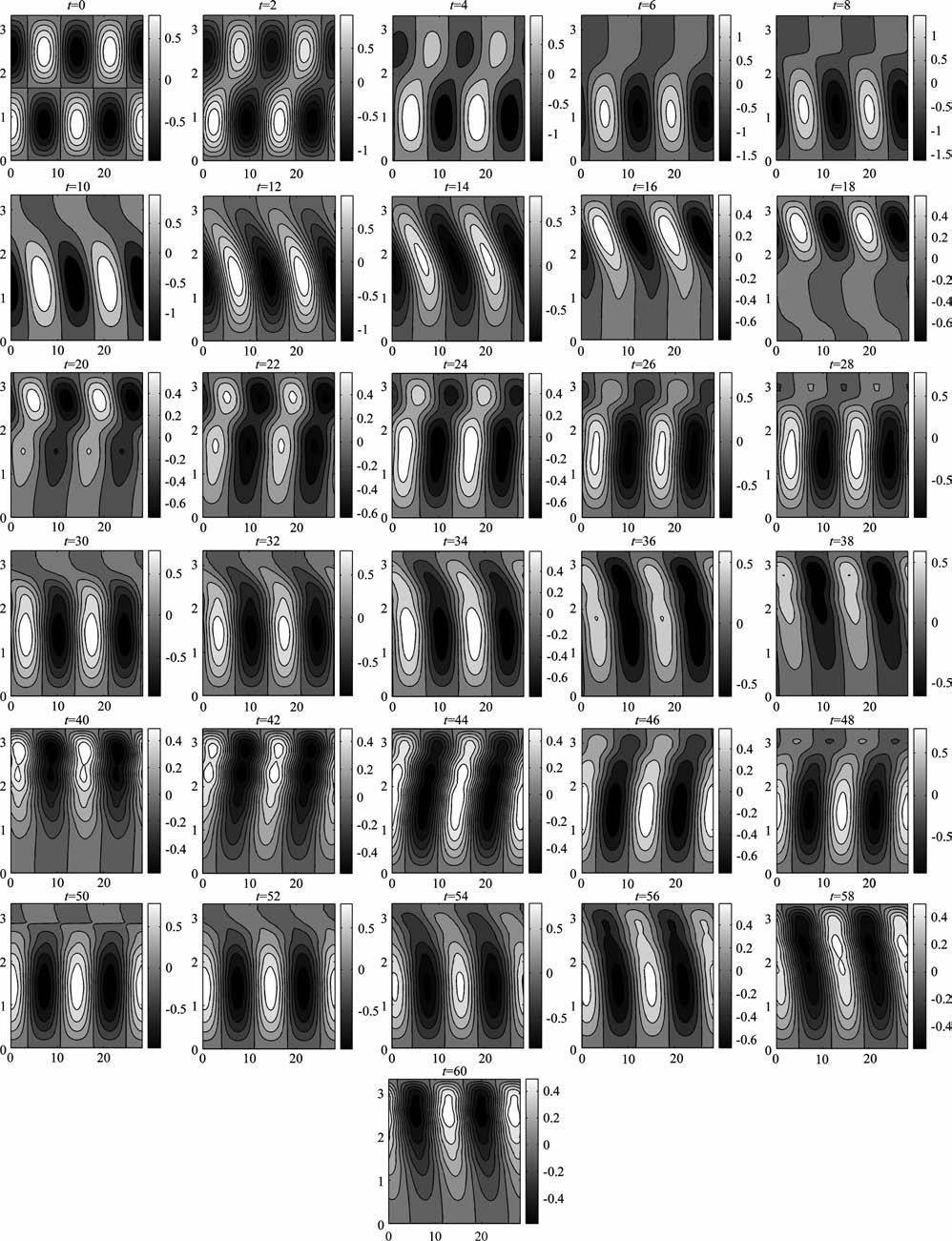
4 线性与非线性Rossby波流场结构的演变对于正压大气而言,波动能量变化的根本原因是流场结构的变化.图 3和4 分别给出了1 月基流情形下,初始场为k=2、m=2 时线性和非线性Rossby波流场结构随时间演变.横坐标为经向无量纲长度,纵坐标为纬向无量纲长度.每幅小图时间间隔为2天,第一幅小图为初始时刻的流场结构.
|
图 3 线性Rossby波流场结构随时间演变(横坐标为经向无量纲长度,纵坐标为纬向无量纲长度) Fig. 3 The evolutions of linear Rossby wave stream field structure with time.The vertical and horizontal coordinate are the non-dimensional length of latitude and longitude, respectively |
分析图 3和图 4可看出,线性Rossby波在总能量增长阶段,槽脊线呈东北-西南向,流函数的极值中心略偏南;在总能量衰减阶段,槽脊线呈西北-东南向,流函数的极值中心略偏北.对应图 2中相对总能量演变中的三个极大值,槽脊线经历了三次转换,流函数极值中心位置经历了三次调整.值得注意的是,在流场的整个演变过程中,纬向上一直维持着与初始场相同的两个标准的正(余)弦波形不变.在经向上,结构由始时一波结构很快演变成半波结构.
对于非线性Rossby 波,它的流场结构演变比较复杂.在经向上,由初始1波调整为半波的时间比线性波长;在纬向结构上,最大的不同是从第16 天起出现了长波调整的现象,第18 天变得明显,从纬向2波演变为4波,波长减小.随后到第34天,流场结构又变为沿纬圈的2 波.对比相对总能量演变图2,可发现第18天是相对总能量快速减小达到极小值的时间,第34 天是能量又增长达到极大值的时间,可以认为在相对总能量减小的过程中,纬向波数增大,在相对总能量增大的过程中纬向波数减小.特别是随纬向波数增大,当k=5 时,非线性波在第4天演变为类似椭圆余弦波结构(图略),并一直演变到第56天.在其演变期间,它的振幅经历了从正振幅绝对值大于负振幅绝对值到负振幅绝对值大于正振幅绝对值的转化.从第56 天开始,出现长波调整现象,即从长波向超长波调整.
对于不同月份的基流和不同初始场结构的波动计算结果发现,上述线性和非线性波动流场演变特征都存在,只是非线性波动出现长波调整时,调整的时间不同.
综上分析可知,线性Rossby波与非线性Rossby波演变过程的主要差别在于线性波在整个过程中保持纬向波数不变,经向变为半个波,可根据流场和基流的结构来判断相对总能量是否增长;而非线性波在演变过程中,流场结构的变化多样,既可出现类似椭圆余弦波结构,又可出现长波调整现象,且伴随调整,相对总能量振荡增长和衰减的频率明显增加.
5 初值对线性与非线性Rossby波演变的影响在(2)式的初始场上叠加一个小扰动,形成如下初值:
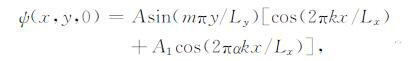
|
(7) |
其中α 为非负整数,A1 为常数.显然当α 取不同值时,表示叠加了不同尺度扰动.
计算中分别取α=0、α=2、α=3和α=4代表四种不同的初始场,为了保证叠加的是小扰动,A1 的取值如下:

|
(8) |
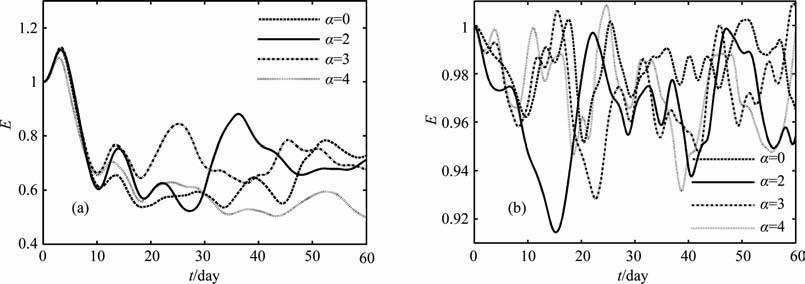
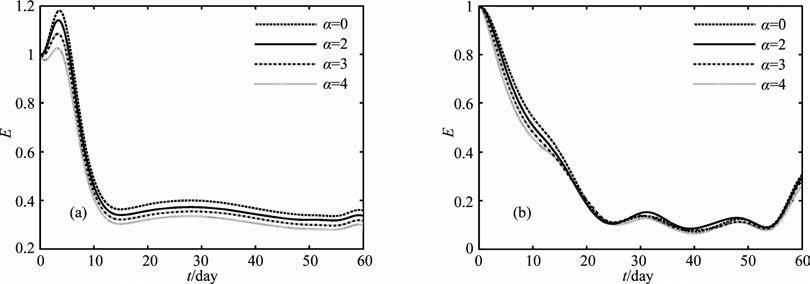
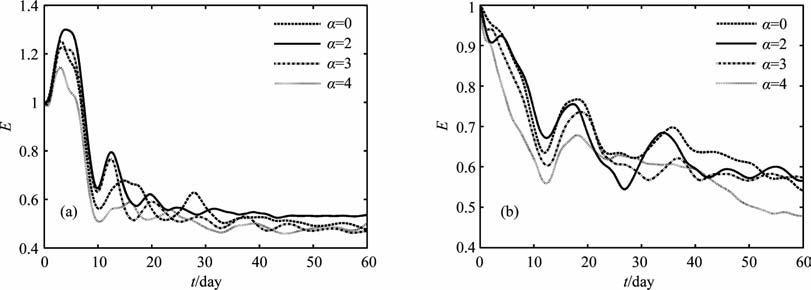
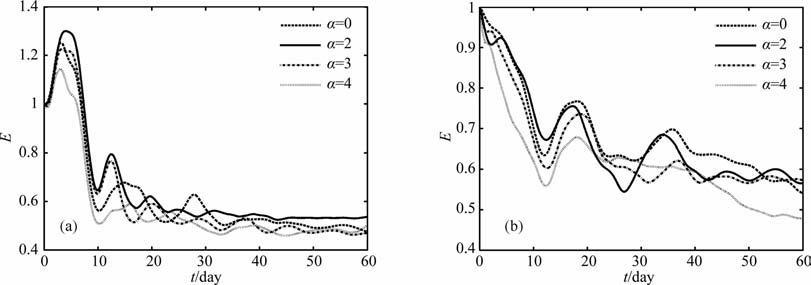
图 5和图 6分别给出了k=3,m=2时,图 7和图 8分别给出了k=6,m=2时,在冬夏两季基流和不同初始场情形下,线性Rossby波(LE)和非线性Rossby波(NE)相对总能量随时间的演变.
|
图 5 k=3,m=2时,冬(a)夏(b)季基流和不同初始场情形LE 相对总能量随时间的演变 Fig. 5 The evolutions of LE for different initial fields in winter (a) and summer (b) when k== and m=2 |
|
图 8 k=6,m=2时,NE 相对总能量随时间的演变,说明同图 5 Fig. 8 The evolutions of NE for different initial perturbation fields when k = ^and m=2.Same as Fig.5 |
由图可以看出,对于线性波,在相同的基流情形下,无论纬向波数是长波还是超长波对初值都不敏感,不论α 取何值,相对总能量随时间演变的差异很小.而初始场为m=1时(图略),长波和超长波的相对总能量大小在某些时刻随α 不同有差异,但其演变趋势几乎是一样的,这说明在相同的基流情形下,线性Rossby波相对总能量的演变对初值是不敏感的,其演变特征决定于基流的分布.从可预报性角度考虑,可以认为线性Rossby波是可预报的,若实际大气中某些天气系统主要由线性Rossby 波控制,那么其可预报性是强的.
非线性Rossby波相对总能量的演变对初始场是非常敏感的,在相同的基流情形下,不同的α 对应的能量演变曲线明显不同.这也说明非线性Rossby波的演变强烈依赖于初始场结构.特别要注意的是对于不同的α ,相对总能量在演变过程中出现了曲线“分叉"现象,这类似于混沌现象,所以线性Rossby波的演变更主要的依赖于基流分布,而非线性Rossby波的演变不仅依赖于基流结构,还依赖于初始场结构.
实际大气中长波槽脊的演变可通过非线性Rossby波来描述,而非线性波对初值的敏感性可导致天气系统预报结果对初值的敏感.实际天气预报中,数值模式的初始场不可避免的存在小误差,这就可能造成预报结果发生很大的变化,从而影响预报的精度.所以精确的初值是提高数值预报水平的关键问题之一,解决这个问题的有效途径是发展初值同化技术和集合预报技术.
6 结论本文针对准地转正压位涡方程自行设计了数值求解的差分格式,通过双Gauss函数拟合方法得到了1、4、7月和10月的北半球真实基流的拟合函数,计算和分析了不同基流情形下的线性和非线性Rossby波的演变特征及初值对其的影响,主要结论有:
(1) 不同初始场决定了线性和非线性Rossby波相对总能量能否在有限时段内快速增长.在真实基流情形下,线性和非线性Rossby 波的相对总能量在演变过程中都可出现振荡型增长和振荡型衰减的现象.
(2) 在相同的基流和初始场的情形下,一般而言,如果波动的相对总能量在有限时段内快速增长,那么线性Rossby波的相对总能量的最大值大于非线性Rossby波;如果在有限时段内出现衰减,那么线性Rossby波相对总能量的衰减速度也大于非线性Rossby波.这表明,非线性项不仅能够抑制能量的快速发展同时也抑制能量的快速衰减.
(3) 在相同的基流和初始场情形下,与线性波相比,非线性Rossby波在相对总能量的演变中,出现振荡型增长和振荡型衰减的次数明显增多.线性Rossby波相对总能量的振荡周期一般为20-30天,非线性Rossby 波相对总能量的振荡周期一般为15-20天.
(4) 真实基流情形下,非线性Rossby波的流场结构的演变与线性Rossby 波也明显不同,它不是以标准的正弦(或余弦)波动方式变化,而是以类似椭圆余弦波的方式演变,且在它的演变过程中,会出现长波调整的现象.
(5) 对非线性Rossby波来说,基流分布和初始场对其演变特征都有很大影响,特别是对初始场的变化非常敏感,在其能量演变过程中,可能出现类似混沌的现象.
| [1] | Lin C C. The Theory of Hydrodynamic Instability. 1955 : 155 . |
| [2] | Charney J G. The dynamics of long waves in a baroclinic westerly current. J Meteor , 1947, 4: 135-162. |
| [3] | Eady E T. Long wave and cyclone waves. Tellus , 1949, 1: 33-52. DOI:10.1111/tus.1949.1.issue-3 |
| [4] | Kuo H L. Dynamic instability of two-dimensional non-divergent flow in a barotropic atmosphere. J Meteor , 1949, 6: 105-122. DOI:10.1175/1520-0469(1949)006<0105:DIOTDN>2.0.CO;2 |
| [5] | Hoskins B J, Karoly D. The steady linear response of a spherical atmosphere to thermal and orographic forcing. J Atmos Sci , 1981, 38: 1179-1197. DOI:10.1175/1520-0469(1981)038<1179:TSLROA>2.0.CO;2 |
| [6] | Pedlosky J. An initial value problem in the theory of baroclinic instability. Tellus , 1964, 16: 12-17. DOI:10.1111/tus.1964.16.issue-1 |
| [7] | Burger A P. Instability associated with the continuous spectrum in a baroclinic flow. J Atmos Sci , 1966, 23: 443-469. DOI:10.1175/1520-0469(1966)023<0443:TAROTS>2.0.CO;2 |
| [8] | Tung K K. Initial-value problems for Rossby waves in a shear flow with critical level. J Fluid Mech , 1983, 133. |
| [9] | Orr W M. The stability or instability of the steady motions of a liquid. Proc.R.Irich Acad. , 1907, A27: 69-138. |
| [10] | Rosen G. General solution for perturbed plane Couette flow. Phy. Fluids , 1971, 14: 2767-2769. DOI:10.1063/1.1693404 |
| [11] | Farrell B F. Transient growth of damped baroclinic waves. J.Atmos.Sci. , 1985, 42(24): 2718-2727. DOI:10.1175/1520-0469(1985)042<2718:TGODBW>2.0.CO;2 |
| [12] | Boyd J P. Equatorial solitary waves. J.Phys,Oceanogr , 1980, 10: 1699-1717. DOI:10.1175/1520-0485(1980)010<1699:ESWPIR>2.0.CO;2 |
| [13] | Zeng Q C. On the evolution and interaction of disturbances and zonal flow in rotating barotropic atmosphere. J.Meteor.Soc.Japan, Ser. II , 1982, 60: 24-31. |
| [14] | Zeng Q C. The development characteristics of quasi-geostrophic baroclinic disturbances. Tellus , 1983, 35: 337-349. |
| [15] | 卢佩生, 曾庆存. 正压大气中扰动的演变. 大气科学 , 1981, 5(1): 1–8. Lu P S, Zeng Q C. The evoluement of disturbance in barotropic atmosphere. Chinese Journal Atmosphere Science (in Chinese) , 1981, 5(1): 1-8. |
| [16] | Farrell B F. Optimal excitation of neutral Rossby waves. J.Atmos.Sci. , 1988, 45(2): 163-172. DOI:10.1175/1520-0469(1988)045<0163:OEONRW>2.0.CO;2 |
| [17] | Farrell B F. Optimal excitation of baroclinic waves. J.Atmoc.Sci. , 1989, 46(9): 1193-1207. DOI:10.1175/1520-0469(1989)046<1193:OEOBW>2.0.CO;2 |
| [18] | Farrell B F, Ioannou P J. Structure and spacing of jets in barotropic turbulence. J. Atmos. Sci. , 2007, 61: 3652-3665. |
| [19] | Farrell B F, Ioannou P J. Formation of jets by baroclinic turbulence. J.Atmos.Sci. , 2008, 62: 3353-3375. |
| [20] | 张亮, 张立凤, 吴海燕, 等. 正压Rossby波扰动能量. 物理学报 , 2010, 59(1): 44–53. Zhang L, Zhang L F, Wu H Y, et al. The disturbance energy of barotropic Rossby wave. Acta Physica Sinica (in Chinese) , 2010, 59(1): 44-53. |
| [21] | Tung K K. Initial-value problems for Rossby waves in a shear flow with critical level. J Fluid Mech , 1983, 133: 443-469. DOI:10.1017/S0022112083002001 |
| [22] | Geisler J E, Dickinson R E. External Rossby modes on a β-plane with realistic vertical wind shear. J Atmos Sci , 1975, 32: 2082-2093. DOI:10.1175/1520-0469(1975)032<2082:ERMOAW>2.0.CO;2 |
| [23] | Hoskins B J, Ambrizzi T. Rossby wave propagation on a realistic longitudinally varying flow. J Atmos Sci , 1993, 50(12): 1661-1671. DOI:10.1175/1520-0469(1993)050<1661:RWPOAR>2.0.CO;2 |
| [24] | Redekopp L G, Weidman P D. Solitary Rossby waves in zonal shear flows and their interactions. J Atmos Sci , 1978, 35: 790-804. DOI:10.1175/1520-0469(1978)035<0790:SRWIZS>2.0.CO;2 |
| [25] | Zhang L, Huang S X, Zhang L F. Numerical experiments about growth of disturbance energy of potential vorticity equation within finite time scope. Proceedings of the 5th International Conference on Nonlinear Mechanics (ICNM-V), : Shanghai University Press, 2007 : 1195 -1200. |
 2011, Vol. 54
2011, Vol. 54