2. 成都理工大学沉积地质研究院,成都 610059;
3. 中石油川庆钻探工程有限公司地球物理勘探公司,成都 610213
2. Institute of Sedimentary Geology, Chengdu University of Technology,Chengdu 610059, China;
3. Geophysical Exploration Company, Chuanqing Drilling Engineering Co. Ltd., CNPC, Chengdu 610059, China
利用地震资料直接进行储层流体识别已成为地震储层预测技术的主流发展方向及勘探地球物理领域的研究热点之一.由于地震观测数据直接表现为岩石的声学特征(振幅),并不是储集层的直接反映,尽管我们可以通过各种反演方法得到各种储集层参数,但这是一个高度的非线性映射关系,反演具有多解性.另外,储层中油、气、水等流体性质差异极其微弱,因此,利用地震资料直接进行流体识别也是一个非常难的问题.迄今为止,国内外相关学者开展了大量的研究工作,比较有效的方法主要包括叠后属性分析,常规AVO 分析、弹性阻抗、弹性参数等叠前反演技术[1~3],基于吸收衰减理论的参数反演[4]以及各种基于时频分析的谱分解方法[5~7]等.
地震信号的频域属性能够反映传输介质差异的固有特性,不同性质的流体对地震波的吸收、衰减不一样.因此,通过分析信号的时频属性来对储层流体进行预测和识别是一种行之有效的方法.时频谱分解的关键是选择合适的时频分析方法,使之能够有效表征信号的局部特征.常用的时频分析方法有短时傅里叶变换(STFT)[8]、Gabor 变换[9]、小波变换[10~12]、广义S 变换[13, 14]等,然而,这些方法时频聚集性往往不高,分辨率比较低.Wigner-Vile时频分布分辨率较高,但由于受到交叉项的影响,也限制了它的应用范围[15].近年来,一种新的时频分析技术---分数域时频分析方法被提出,由于其较高的能量聚集性、可在不同阶次下进行分频计算等优点成为信号处理领域的一个新的研究热点.
本文在分数阶Fourier变换[16~18]的基础上将分数阶化思想引入到地震信号的时频分析,研究基于分数阶Gabor变换(Fractional Gabor Trans form, FrGT)[19, 20]的地震信号谱分解理论与方法,解决了FrGT 应用中如何确定最优阶的问题.最后,将该方法应用于实际地震信号的时频分析,可获得最优阶下的各个高分辨率的单频剖面.解释结果表明,该方法具有潜在优势,可为地震储层预测,尤其是储层流体识别应用提供一条新的途径.
2 FrGT 变换理论 2.1 经典Gabor变换原理在非平稳信号处理领域,Gabor变换作为最早的时频分析技术之一,为非平稳信号的分析与处理开辟了新的途径.它可以解释对信号的STFT,即用时域窗函数对信号进行截断,对截断后的局部信号作Fourier变换.通过不断滑动窗函数来获取信号不同时刻的频域信息[10].
一维离散信号x(n)= {x1,x2,…,xN-1} 的Gabor展开式如下:

|
(1) |
式中:
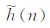

|
(2) |
则信号x(n)的Gabor变换可表示如下:

|
(3) |
式中,
将式(3)代入式(1)得到两者的完备性条件如下式:

|
(4) |
这里n,l取值范围为
Gabor变换能直观地展现信号不同时刻的频率信息,而且不会像Wigner分布那样出现交叉项干扰的情况,因此在时频分析领域应用非常广泛.然而由于受到测不准原理的影响,导致它的时频带宽积无法达到最小,时频分辨率相互制约.
2.2 FrGT理论分数域时频分析源于Namias(1980)从纯数学上推导的分数阶傅里叶变换(Fractional Fourier Trans form, FrFT)[18],因当时无法解释其物理意义,直到Almeida(1994)[19]将其理解为时频面上的旋转后,该方法才得以引起重视.迄今,FrFT 已在光学、盲信号分离、雷达目标检测、语音识别、参数估计等各个领域得到广泛应用[20].FrGT 是在传统Gabor变换的基础上应用分数阶化思想对其进行推广的结果[5].通过引入FrFT 核函数替换原来的核函数,来改善传统的Gaobr变换的性能.
用分数阶核函数Kp(n,k)替换传统Gabor变换核{ejwkn},得到信号的FrGT 展开式如下:

|
(5) |
其中:
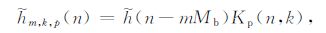
|
(6) |
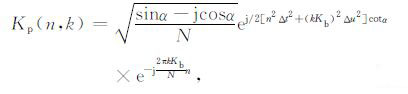
|
(7) |
其中α为旋转角,令α=pπ/2,则p称为分数阶变换的阶数.M,K,Mb, Kb 等参数的含义与式(2)一样.
对应的分数阶Gabor变换为:

|
(8) |
式中,
将式(8)代入式(5)中,则有
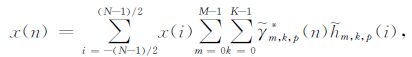
|
(9) |
由上式可以得到分数阶基函数的完备性条件为:
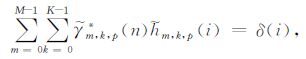
|
(10) |
将
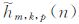

|
(11) |
根据式(11)可求得
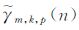
相对传统的Gabor变换而言,通过将时频面旋转角度α =p×π/2(p为对应的阶数),只要选择合适的旋转角度,FrGT 便能够使信号的时频带宽积达到最小,因而它具有很高的时频聚集性,能够很好地检测出信号的局部特征信息.
离散傅里叶变换(DFT)变换是一种将函数f(t)旋转π/2,由t轴变换到ω 轴的表示形式,即函数在与时间轴夹角为π/2 的ω 轴上表示就是该函数的Fourier变换;Gaobr变换所表征的是信号在(t,f)二维平面中的特征.FrGT所表征的则是信号在(t,u)二维平面中特征,如图 1所示.

|
图 1 由(t,f)旋转到(t,u) Fig. 1 (t,f) rotate to (t,u) |
根据分数域采样定理[21]和两者之间的旋转关系,分数域的频率u和Fourier域频率之间的映射关系为u=f×sin(pπ/2).相对传统的Gabor变换而言,通过将时频平面旋转角度α=p×π/2(p为对应的阶数),只要选择合适的旋转角度,分数阶Gabor变换便能够使信号的时频带宽积达到最小,因而它具有很高的时频聚集性,能够很好地检测出信号的局部特征信息.在经过旋转的时频平面内,能有效地解决传统Gabor变换所不能解决的问题,如目标信号的提取,多分量信号检测,最优滤波器设计等.
2.3 最优阶次确定分数域时频分析的优越性主要体现在它的时频聚集性相比传统的时频分析高,而要达到这种效果必须要解决一个关键问题就是如何确定分数域变换的最优阶次.本文从时间-带宽积(Time-BandwidthProduct, TBP)[13]出发,来寻求最优阶.
连续信号x(t)的时间-带宽积定义如下:
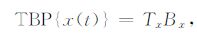
|
(12) |
式中Tx,Bx分别表示时频分析的时宽和频宽.且
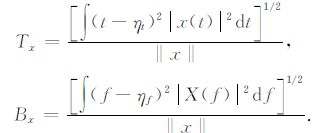
|
(13) |
其中:
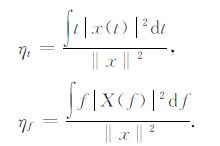
|
(14) |
对式(11)进行拓展得到一种分数域下广义时间-带宽积(Generalized Time-Bandwidth Product, GTBP)的刻画形式,即

|
(15) |
其中,xp(t)为信号的p阶FrGT,Txp =Tx,Bxp则可写为
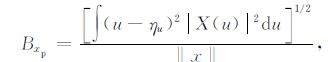
|
(16) |
式中,

|
(17) |
根据紧支撑集原理可知,信号的时间-带宽积的大小可以刻画信号时频聚集性的优劣,从而我们可以通过下式来获取最优阶:

|
(18) |
在最优阶次下,对离散信号进行FrGT,可以获得局部能量聚焦良好的高分辨率频谱特征,这对信号的异常检测、特征分析极其有利.
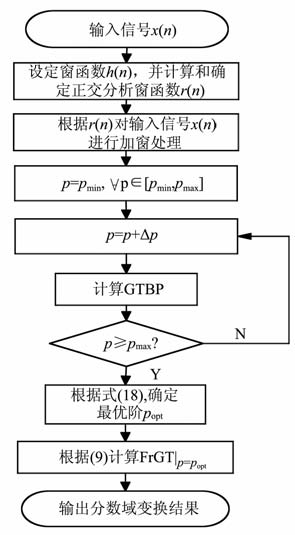
2.4 一维信号FrGT的基本流程FrGT 算法中的关键是最优阶的确定,阶数的选取直接影响算法对信号分析性能.因为FrGT 具有周期性,为了得到最优阶,算法实现过程中可在一个周期内对阶数进行遍历.算法的实现流程如下:
图 2中p,Δp,pmin, pmax分别表示FrGT 的任意分数阶、递增步长、最小阶及最大阶数.popt代表根据GTBP下的最优解.
|
图 2 FrGT的基本流程 Fig. 2 The general flow chart of FrGT |
FrGT 本质上是对FrFT 的加窗处理,是一种短时FrFT,具有FrFT 的所有特点,如周期性,旋转相加性,线性等.不同之处在于在对信号进行FrFT之后,得到的是一维信号,不能反应出信号的频率随时间的变化关系,而FrGT 正是从这点出发,结合传统的Gabor变换和FrFT 的优点,不仅能改善信号的时频分布性能,而且还能直观地得到信号频谱的局部特征,有利于对非平稳信号的分析和处理.

|
(19) |
式(19)为一测试信号,对其分别进行传统Gabor变换和FrGT,以比较其性能.计算中,时间t取-8~8s, 采样率为64,仿真结果如图 3所示.

|
图 3 FrGT数值仿真结果 (a)原始信号;(b)经典的Gabor变换得到的时频谱;(c) f =0.7时对应的分数阶Gabor变换得到的时频谱;(d) p= 1.0时对应的分数阶Gabor变换得到的时频谱;(e)p=1.4时对应的分数阶Gabor变换得到的时频谱;(f)p=1.175时对应的分数阶Gabor变换得到的时频谱. Fig. 3 The result of numerical simulation of FrGT (a) Source signal; (b) The time-frequency spectra of classic gabor transform; (c) The time-frequency spectra of FrGTwhen p = 0.7; (d) The time-frequency spectra of FrGT when p=1.0; (e) The time-frequency spectra of FrGT when p=1.4;(f) The time-frequency spectra of FrGT when p=1.175. |
图中可以看出,当阶数p=1 时,FrGT 与经典Gabor变换结果一致;当按式(18)搜索获得最优阶popt=1.175 时,对应的FrGT 时频聚集性明显提高,见图 3中最右边的图.不同阶数下对应的GTBP如表 1所示.
|
|
表 1 不同阶次下的时频带宽积 Table 1 The GTBP under different order |
从表中看出,最优阶下的GTBP为20.55,为最小支撑集.
4 应用实例分析针对实际地震资料处理,可按以下步骤进行:
(1) 首先,对输入的2D 地震剖面,选取其中的n道,进行最优阶分析,计算得到n个最优阶参数p(i),{i=0,1,2,…,n-1},最后取它们的平均值作为整个剖面的最优阶popt;
(2) 其次,遍历所有地震道数据,进行popt 阶次下的FrGT变换,得到所有地震道的分数域时频分布.
(3) 然后根据地震信号频谱分布范围,提取分数域的单频属性剖面.
(4) 最后根据先验知识,进行储层预测及含流体差异的判定.
为了验证本文方法的有效性,我们选取了川东北地区某碳酸盐鲕滩储层进行了试验.图 4 为某测线CDP 叠加剖面,目的层位于1880~2280 ms, 探井位置位于CDP382,如图中的椭圆标记所示,测井资料及测试结果显示为一含气层.图 5(a~d)分别为对应剖面不同分数域频率下的单频剖面.这里,分数域频率可通过反旋转换算为实际信号的真实频率.

|
图 4 某测线CDP叠加剖面 Fig. 4 A CDP stack section corresponding to one InLine |

|
图 5 基于FKGT谱分解得到的结果 (a)分数域 u= 10,对应的频率f=20 Hz;(b)分数域u= 14,对应的频率f=30 Hz;(c)分数域u= 20,对应的频率f=40 Hz;(d)分数域u= 25,对应的频率f=49 Hz. Fig. 5 The result of spectral decomposition based on FrGT (a) Fractional domain u =10,corresponding frequency f=20 Hz; (b) Fractional domain u =14, correspondingfrequency f=30 Hz; (c) Fractional domain u=20, corresponding frequency f=40 Hz; (d) Fractional domain u=25,corresponding frequency f=49 Hz. |
从图中的单频剖面显示看到,地震主频带范围的能量聚集性很高.对比不同频率的谱分解剖面,在高频部分,储层能量衰减明显,能量聚集性逐渐减弱,进一步验证了地震波的高频端衰减特性.根据这一特性,建立流体识别判据,可为储层流体预测与识别奠定基础.
5 结语本文将分数域时频分析的思想引入到地震信号处理领域,首次提出了一种基于FrGT 的分数域谱分解方法,并应用于地震储层预测及流体识别.由于分数域时频分析方法具有良好的局部时频能量聚集及不同阶次下多尺度分解能力等优点,它能为我们提供高分辨率的频谱剖面及展布流体差异的细微特征.实际资料的处理试验证明了该方法具有潜在优势,可为基于地震资料的储层流体识别提供一条新的思路和途径.
目前FrGT 运算主要借助了FFT 算法,效率相对较低;同时,最优阶只能根据有限的计算道数取平均的方法来确定,应用于整条测线或工区时可能会造成一定的误差.因此,FrGT 的快速算法以及实际应用中的最优阶问题有待进一步研究.
| [1] | 彭真明, 李亚林, 巫盛洪, 等. 叠前弹性阻抗反演在储层气水识别中的应用. 天然气工业 , 2007, 38(4): 43–45. Peng Z M, Li Y L, Wu S H, et al. Application of prestack elastic impedance inversion in gas and water recognition of the reservoir. Natural Gas Industry (in Chinese) , 2007, 38(4): 43-45. |
| [2] | 彭真明, 李亚林, 巫盛洪, 等. 碳酸盐岩储层多角度弹性阻抗流体识别方法. 地球物理学报 , 2008, 51(3): 881–885. Peng Z M, Li Y L, Wu S H, et al. Discriminating gas and water using multi-angle extended elastic impedance inversion in carbonate reservoirs. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 881-885. |
| [3] | 彭真明, 李亚林, 魏文阁, 等. 粒子滤波AVO非线性反演方法. 地球物理学报 , 2008, 51(4): 1218–1225. Peng Z M, Li Y L, Wei W G, et al. Nonlinear AVO inversion using particle filter. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1218-1225. |
| [4] | 徐天吉, 程冰洁. 基于吸收滤波技术的储层气水性质识别方法. 地球物理学进展 , 2009, 24(5): 1787–1793. Xu T J, Cheng B J. Methodology of distinguishing gas and water in reservoirs based on absorption filtering technology. Progress in Geophysics (in Chinese) , 2009, 24(5): 1787-1793. |
| [5] | 陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测. 地球物理学报 , 2009, 52(1): 215–221. Chen X H, He Z H, Huang D J, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 215-221. |
| [6] | 朱振宇, 吕丁友, 桑淑云, 等. 基于物理小波的频谱分解方法及应用研究. 地球物理学报 , 2009, 52(8): 2152–2157. Zhu Z Y, Lü D Y, Sang S Y, et al. Research of spectrum decomposition method based on physical wavelet transform and its application. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2152-2157. |
| [7] | 刘喜武, 宁俊瑞, 刘培体, 等. 地震时频分析与分频解释及频谱分解技术在地震沉积学与储层成像中的应用. 地球物理学进展 , 2009, 24(5): 1679–1688. Liu X W, Ning J R, Liu P T, et al. Seismic time-frequency analysis for frequency decomposition with applications to seismic sedimentology and reservoir imaging. Progress in Geophysics (in Chinese) , 2009, 24(5): 1679-1688. |
| [8] | Durak L, Arikan O. Short-time Fourier transform: two fundamental properties and an optimal implementation. IEEE Transaction on Signal Processing , 2003, 51(5): 1231-1242. DOI:10.1109/TSP.2003.810293 |
| [9] | Wexler Raz. Discrete Gabor expansions. Signal Processing , 1990, 21(3): 207-221. DOI:10.1016/0165-1684(90)90087-F |
| [10] | Sinha S, Partha S, Anno P D, et al. Spectral decomposition of seismic data with continuous-wavelet transform. Geophysics , 2005, 70(6): 19-25. DOI:10.1190/1.2127113 |
| [11] | Sinha S, Partha S, Anno P D. Instantaneous spectral attributes using scales in continuous-wavelet transform. Geophysics , 2009, 74(2): 137-142. DOI:10.1190/1.3054145 |
| [12] | Wang Y. Seismic time-frequency spectral decomposition by matching pursuit. Geophysics , 2007, 72(1): 13-20. |
| [13] | 高静怀, 陈文超, 李幼铭. 广义S变换与薄互层地震响应. 地球物理学报 , 2003, 46(4): 526–532. Gao J H, Chen W C, Li Y M. Generalized S transform and seismic response analysis of thin interbeds. Chinese J. Geophys. (in Chinese) , 2003, 46(4): 526-532. |
| [14] | 甄莉, 彭真明. 基于广义S变换的图像局部时频分析. 航空学报 , 2008, 29(4): 1013–1019. Zhen L, Peng Z M. Local time-frequency analysis of images based on generalized S-transform. Acta Aeronautica Et Astronautica Sinica (in Chinese) , 2008, 29(4): 1013-1019. |
| [15] | Lee J H, Kim J, Kim H J. Development of enhanced Wigner-Ville distribution function. Mechanical Systems and Signal Processing , 2001, 15(2): 367-398. DOI:10.1006/mssp.2000.1365 |
| [16] | Namias V. The fractinal order Fourier transform and its application to quantum mechanics. J Inst Math Appl , 1980, 25: 241-265. DOI:10.1093/imamat/25.3.241 |
| [17] | Almeida L B. The fractional Fourier transform and time-frequency representations. IEEE Tran Signal Processing , 1994, 42(11): 3084-3091. DOI:10.1109/78.330368 |
| [18] | 陶然, 邓兵, 王越. 分数阶Fourier变换在信号处理领域的研究进展. 中国科学 E集:信息科学 , 2006, 36(2): 113–136. Tao R, Deng B, Wang Y. The researching progress of fractional Fourier transform in the field of signal processing. Science in China Series E: Information Sciences (in Chinese) , 2006, 36(2): 113-136. |
| [19] | Cekic Y, nen E. A fractional Gabor expansion. Journal of the Franklin Institute , 2003, 340(5): 391-397. DOI:10.1016/j.jfranklin.2003.08.004 |
| [20] | Cekic Y, nen E. A discrete fractional Gabor expansion for multi-component signals. AEU-International Journal of Electronics and Communications , 2007, 61(5): 279-185. DOI:10.1016/j.aeue.2006.05.001 |
| [21] | 张卫强, 陶然. 分数阶傅立叶变换域上带通信号的采样定理. 电子学报 , 2005, 33(7): 1196–1199. Zhang W Q, Tao R. Sampling theorems for bandpass signals with fractional fourier transform. Acta Electronica Sinica (in Chinese) , 2005, 33(7): 1196-1199. |
 2011, Vol. 54
2011, Vol. 54


