2. 中国人民解放军驻航天科工集团二院军事代表室, 北京 100854;
3. 中国人民解放军驻中国电子信息产业集团12院军事代表室, 北京 100846
2. Military Representative Office of PLA in Second Research Institute of CASIC, Beijing 100854, China;
3. Military Representative Office of PLA in Twelfth Research Institute of CEC, Beijing 100846, China
核函数理论的研究可以追溯到1909年,Mercer[1]在泛函分析中提出了再生核(Mercer核)和再生核Hilbert空间.1950年,Aronszajn[2]对其进行了进一步完善.1964年,Aizerman等[3]将再生核技术用于学习理论的证明.1995年,Vapnik等[4]将统计学习理论与核技术相结合,构建了一种新的核方法-支持向量机,它在分类、回归和预测等方面已取得了广泛的应用.支持向量机中常用的核包括线性核、多项式核、高斯径向基函数核以及sigmoid核函数等.近年来,随着对核方法的深入研究,针对多数据源或异构数据集问题,Sonnenburg 等[5]提出了多核学习.针对地震勘探信号处理这一应用问题,邓小英等[6~8]提出了适合于地震信号处理的Ricker子波核函数,利用Ricker子波核LS-SVR 滤波方法压制地震勘探资料中的强随机噪声,提出了相关的参数选择方案,讨论了Mercer条件在实际应用中的拓展问题,并提出二维Ricker子波核方法以进一步改善滤波效果.结果表明Ricker子波核LS-SVR 方法滤波性能优于高斯径向基函数核LS-SVR、f-x预测滤波、小波变换以及Wiener滤波等常用的方法.
在消减地震勘探记录道和剖面中的随机噪声处理中,通常用信噪比、有效子波畸变程度等物理量度量滤波效果[9].滤波方法作为一种处理信号的过程,除了那些常规的物理量之外,尚有几项也用于衡量处理效果和处理能力的物理量,诸如计算速度、收敛性、稳定性、稳健性、灵敏度等[10].其中稳健性(Robustness)是度量系统在输入信号包含异常点值时的处理效果.一般待处理的信号包含异常点是可能的(如成像异常值、各类不理想校正结果、多次波消除的异常值等等),当异常点值小时可当噪声对待,但当异常值较大时则需要单独考虑.稳健性即是衡量系统处理这类异常点值的能力[11, 12].Ricker核LS-SVR 方法是一种滤波系统,也需要讨论这种处理过程的稳健性及其改善方式,为提高该滤波技术的能力奠定理论基础.本文首先通过分析与仿真实验得出一般的Ricker核LS-SVR 滤波方法与其他相近的核函数LS-SVR 一样,其稳健性不理想.然后进一步提出一类比较理想的权函数辅助该滤波方法,使加合理权函数后的Ricker 核LS-SVR 方法具有较好的稳健性.
2 Ricker子波核LS-SVR 滤波方法及其稳健性讨论 2.1 稳健性与影响函数信号处理过程的稳健性指当输入信号有扰动时引起处理结果的变化程度,即若信息的改变引起处理结果的较大变化,则该处理过程的稳健性差.该特性在地震勘探信号数字处理中都具有比较重要的作用,例如滤波等处理过程对叠加在有效信号上的由各类噪声引起的不规则强振幅是否具有稳健性,需要逐步讨论.
研究信号处理过程的稳健性常使用影响函数(Influence Function, IF)[13, 14].影响函数是统计学中的概念,最早影响函数用于刻画估计量的渐进程度[13, 15],后来用IF 比较估计量对扰动的敏感程度以及对估计处理过程进行稳健性分析[16].
定义1 影响函数(IF):设观测信号的理想概率密度为P,信号处理器(或泛函或统计估计)为T(·),相应的处理输出为T(P),若实际观测信号的概率密度有如下的污染形式Pε,z= (1-ε)P+εΔz,Δz 表示点z处的Dirac分布,那么在z处对概率分布P信号处理器T的影响函数定义为[13, 16]
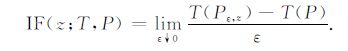
|
(1) |
(1) 式表明,IF(z;T,P)测量在z处无限小量扰动(contamination)对T的影响.这里通常假设概率密度P是正态分布;ε→0 是一个极限状态,在有限采样n计算过程中,常取ε=1/n;可以近似地认为,影响函数IF是信号处理器T在概率分布P处的一阶导数,因此IF是某种意义的变化率,它刻画了信号处理器T对概率分布扰动的敏感程度,若IF 有界,则认为T具有稳健性,否则不具有稳健性[16].
2.2 Ricker子波核LS-SVR滤波方法及其稳健性讨论首先简单概述Ricker 子波核LS-SVR 滤波方法[8].
对观测数据(xi,yi)∈Rd×R(i=1,2,…,l),设回归函数为
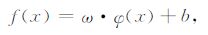
|
(2) |
其中ω 是回归系数向量,φ(x)是非线性映射算子,b∈R 是偏差项,{·}是内积.LS-SVR的约束优化问题为

|
(3) |
其中γ 是正则化参数,ei(i=1,2,…,l)是误差变量.采用拉格朗日乘子法求解该约束优化问题,经过求解线性方程组得到拉格朗日乘子向量α = (α1,α2…,αl)和偏差b,则可得回归函数
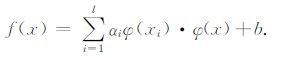
|
采用满足Mercer条件的核函数K(·,·)来代替映射函数在任意两点上的内积φ(xi)·φ(xj)= K(xi,xj),则回归函数可表示为
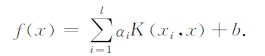
|
(4) |
当核函数应用Ricker子波核[7]
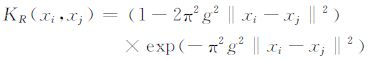
|
(其中g为核参数)时,上述回归处理过程即称之为Ricker子波核LS-SVR 滤波方法,f(xi)(i=1,2,…,l)为滤波结果.
利用式(4)和定义1,在平方损失函数L(y,f(x))= (f(x)-y)2 条件下,可得Ricker子波核LS-SVR 滤波过程的IF[11],它由两项组成,第一项与z= (x,y)的两分量无关(其中x为观测时间,y为观测值),而第二项为
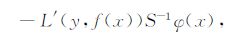
|
(5) |
其中算子S-1 与z无关,φ(x)是前面所述的非线性映射函数.若核函数K(·,·)有界,则φ(x)必有界.而对Ricker子波核函数KR(·,·),利用函数求极值方法可求得-2e-3/2≤ KR(·,·)≤ 1,很明显Ricker子波核函数是有界的,且很快衰减为0,因而φ(x)有界.但是L′(y,f(x))= [(f(x)-y)] 2′ =2(f(x)-y)无界,所以Ricker子波核LS-SVR 滤波过程的IF无界,表明该过程稳健性差.其无界IF由L′造成,它的数量级∝ |(f(x)-y)| .
对于加权Ricker子波LS-SVR,其影响函数IF包括三项[11, 12],第一项独立于z,不影响IF 的性质;第二项包括S1 与IF0(S1(IF0))两部分,S1 是回归计算的算子,IF0 是未加权回归的影响函数.若IF0无界,而回归函数f收敛(这是可以满足的条件),在S1 作用下,则S1(IF0)是有界的.关键是第三项,即
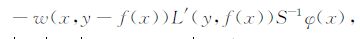
|
(6) |
已知|L′| ∝ |(f(x)-y)| ,S-1φ(x)有界.(6)式的有界性则取决于w(x,y-f(x)).即w的变化有可能抵消|L′| 的无界影响.设w(x,y-f(x))独立于x,即仅为(y-f(x))的函数,且w(y-f(x))=
实际上,IF 的无界性是个极限状态,具体的信号处理过程不是极限状态.无界性使得当信号有异常时处理过程的IF 增加较大,引起差的稳健性.在这种信号处理过程中,则需要改善IF,增加处理的稳健性.例如用加合理的权,则可以改善过程的稳健性.关于在满足权w的一般要求条件下选定优化的权仍是问题.本文将进行这方面的研究工作,借此提高信号处理效果.
3 加权Ricker子波核LS-SVR 方法的稳健性实验研究为了表征Ricker子波核LS-SVR 滤波过程的稳健性程度,先比较不加权Ricker子波核LS-SVR(因以下实验均使用Ricker子波核函数,所以以下简称为不加权SVR)与加权Ricker子波核LS-SVR(以下简称为加权SVR)技术的稳健性;对于加权SVR,进行改变权函数的实验,以期得到更理想的权函数表示式;再考察在不同强度噪声背景中理想权函数滤波的稳健性.
3.1 加权与不加权SVR滤波方法的稳健性实验分析(1) 资料准备
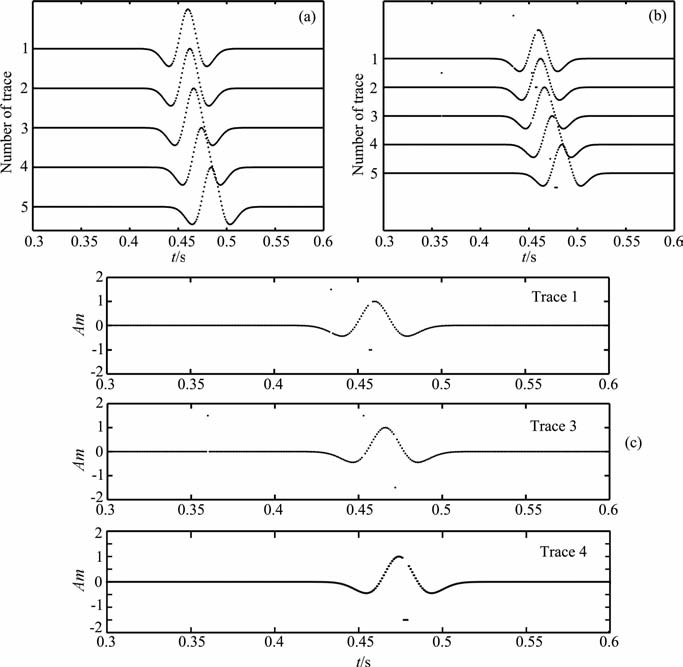
首先合成5道记录,各道的子波相同,Ricker子波主频20 Hz, Δt=1 ms(图 1a).然后对其中的第1、3、4 道的不同时刻加入异常点,如图 1b所示.为了更清晰地显示出异常点,图 1c分别显示了抽出含异常点的第1、3、4道的波形.
(2) 处理结果
对图 1b所示的含异常点记录用未加权和加权SVR 进行滤波,使用logistic 权函数w(r) =tanh(r)/r,其中r为含异常点记录振幅值与未加权SVR 回归值差的绝对值.图 2分别显示了有异常点的第1、3、4道经加权与未加权SVR 滤波结果.第1道(a):子波右波谷位置几乎相同,对左波谷,“加权结果"明显优于“不加权结果";对于波峰,加权结果要好于不加权结果.对三个异常点(用“+"表示),加权结果比不加权结果恢复的要好.第3道(b):其结果与第1道基本相同.第4 道(c):子波左波谷位置几乎相同,对右波谷,加权结果好于未加权结果,对于异常点的恢复效果,加权结果明显要好于未加权结果.总之,经过加权的SVR 滤波处理的稳健性程度较高.
|
图 1 用于比较稳健性的原始数据道 (a) 5道不含异常点的记录;(b) 5道含异常点的记录;(c) 1,3,4道抽在一起. Fig. 1 Original data for use in comparison on the robustness (a) Five traces without outliers;(b) Five traces with outliers; (c) Gathers by sorting traces 1,3 and 4. |
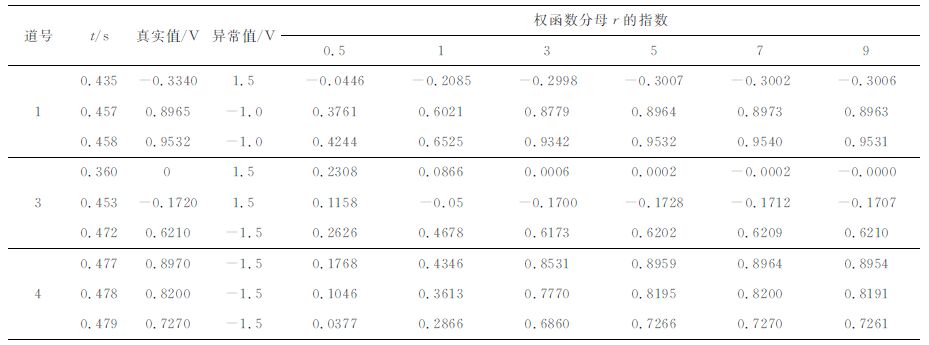
从式(6)出发,分析得到的权函数条件包括权函数的实偶函数性质,以及‖wr‖有界等.满足这些条件的函数不唯一.Debruyne等[11]利用logistic权函数加权得到了比其他如Hampel权函数优越的奇异点恢复结果.我们在此基础上,以满足对权函数的条件为前提,进一步调整tanh(r)/r,以期获得更好的稳健性.调整方式限于两类,即分母r的幂次(用n表示)与系数(用a表示).所用数据同于图 1c.
(1) 改变tanh(r)/r分母r为rn(n=0.5,1,3,5,7,9)
图 3是一组改变幂次n的加权处理结果,分别对应第1、3、4道.对第1道(图 3a):与n=0.5相应的结果(包括波峰位置、幅值,波谷位置、幅值,以及异常点恢复)不如n=1以及未加权的处理;n=1的结果优于未加权的处理;n=3,5,7,9 的结果优于n=1的结果;n=3与n=5,7,9的结果非常接近,未受到异常点的影响,几乎完全恢复到不含异常点的子波波形.对第3 道(图 3b):其比较的结论与第1道的几乎相同.对第4道(图 3c):在波峰处n=3的结果接近n=5,7,9的结果,而n=0.5,1与未加权的结果在波峰附近向左偏移,相比之下第1 道的相应结果向右偏移.上述处理结果表明,使用与幂次n=3相应的权函数加权处理结果已经得到较理想的稳健性.

|
图 2 相对图 1c三道记录经未加权与加权SVR处理结果比较 (a)第1道;(b)第3道; (c)第4道. Fig. 2 Comparison between results obtained by using the unweighted and weighted SVR for three traces in Fig.1c (a) Trace 1 ; (b) Trace 3 ; (c) Trace 4. |
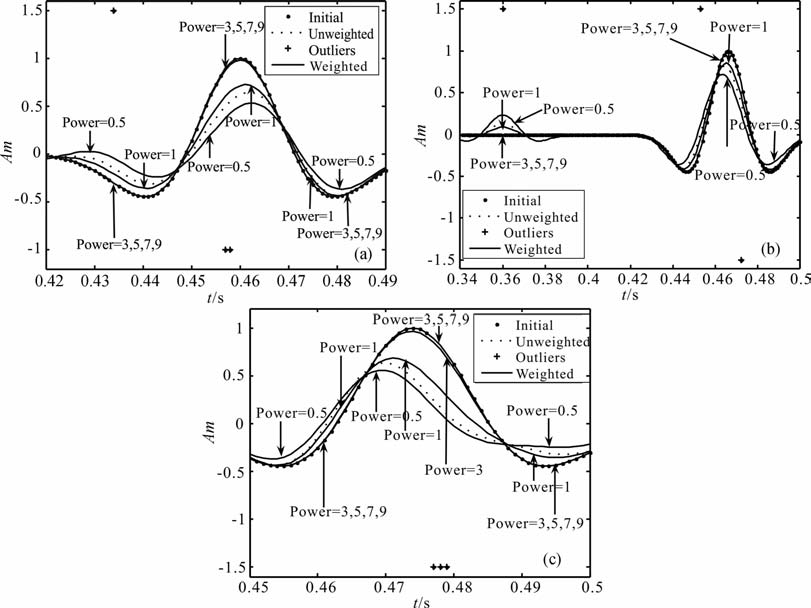
|
图 3
对于权函数 |
为了集中比较改变r幂次n的效果,将第1、3、4道的不同异常点的恢复情况列成表 1.由表 1 可见,对第1道第1异常点(t=0.435s),恢复较好的前4种n是5、9、7、3;第2异常点(t=0.457s),恢复较好的前4种n是:5、9、7、3;第3异常点是5、9、7、3.对第3道和第4 道也很容易得出各自的结果.相比之下,n=7与n=5接近,并且优于n=9与n=3.对n=5与7,考虑到n=7的计算量明显大于n=5的,因此就选择r的幂次而言,选择n=5较适宜.
|
|
表 1 权函数分母r变幂次(rn)3道记录异常点的回归值比较 Table 1 Comparison on regression values of outliers in three traces obtainedby changing the power of denominator of weighted function |
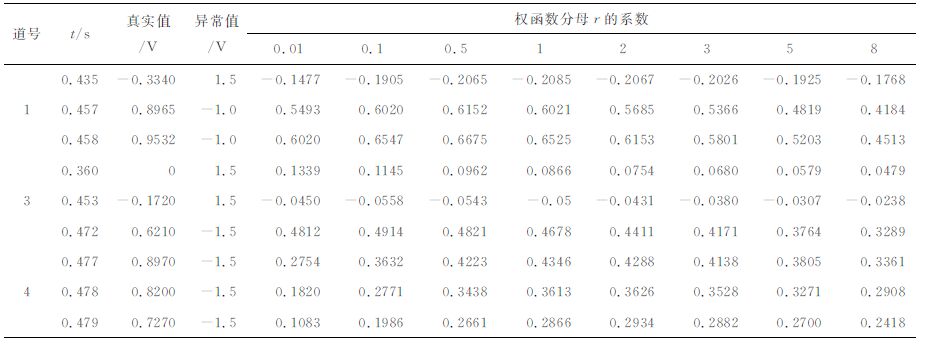
(2) 改变tanh(r)/r的分母r的系数a(0.01,0.1,0.5,1,2,3,5,8)
用表 2说明改变分母r系数a的结果.由表 2可见,a=0.1,0.5,1,2四种系数的结果优于与其他a相应的结果.由于这4种a的结果比较接近,故选择a=1作为分母r的系数即可.
|
|
表 2 权函数分母r变系数3道记录异常点的回归值比较 Table 2 Comparison on regression values of outliers in three traces obtained by changing the coefficient of denominator of weighted function |
综合上述两类实验结果,选择w(r)=tanh(r)/r5作为加权SVR 滤波方法的权函数是较适宜的.注意上述实验结果(a=1,n=5)仅是权函数w(·)的一种合理的表达式.为了节约计算成本,在以下的实验中我们选择计算量更小但回归结果接近的权函数tanh(r)/r3.
3.3 加权VR对不同强度噪声的适应能力限于篇幅仅以图 1c中第1道记录为例,对该道记录叠加功率(σ2)分别为0、0.005、0.008、0.010、0.015、0.020、0.025、0.030、0.040、0.045、0.050、0.100、0.200 W 的高斯白噪声,图 4a示范性地给出了高斯噪声功率为0.05W时的含噪子波,此时子波波峰、波谷的位置和幅值都已发生较大变化,波峰附近的2个异常点使波峰变化更为剧烈.用w(r)=tanh(r)/r3 的加权SVR 分别处理这些既含随机噪声又含异常点的记录,处理结果如图 4b所示.
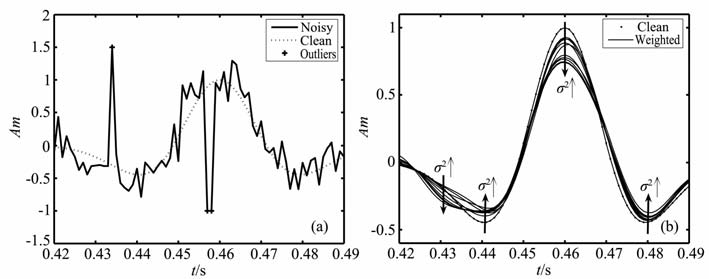
|
图 4 相同权函数w(r) = tanh(r)/r3对不同功率随机噪声条件下的回归结果 (a)髙斯噪声为0.050 W的含噪子波;(b)髙斯噪声分别为0〜0.2 W(13种)采用同一权函数处理后子波. Fig. 4 Regression results obtained by using the same weighted function w(r) = tanh(r)/r3 for noisy wavelets with different noise levels (a) Noisy wavelet contaminated by Gaussion white noise with variance 0.05 W; (b) Wavelets obtainedby using the same weighted function for noisy wavelets with different noise levels. |
由图 4b可见,随着随机噪声功率的增大,波峰波谷的“相位"(即到达时)基本未变,即加权处理具有良好的同相性;但是波峰幅值与波谷幅值在变小.同时由异常点值引起的原子波变化,经加权处理基本恢复了比较正常的波形,表明加权滤波处理在加噪条件下具有良好的稳健性.
为了更清楚表明加权处理在加噪条件下的效果,对图 4b的结果提取出相应的物理量进行了细致比较(表 3).信噪比:由去噪前后信噪比值可得到信噪比改善值变化为17.6、15.8、15.2、14.8、13.9、13.3、12.6、11.9、11.1、10.9、10.9、10.1、10.4dB,表明出现个别异常点值并未改变方法的去噪效果.异常点(表中是以第2 个异常点为例而给出的):总的来看,异常点处幅值基本都得到恢复,处理后与初始子波准确值相差最大仅为0.2(由相差1.9 变到0.2),说明处理过程具有良好的稳健性.波峰变化:其时间位置绝大多数噪声强度背景下都得到准确恢复(仅σ2=0.005 W 时位置滞后一个样点);波峰幅值虽然都变小,但在σ2<0.025 W 条件下,幅值恢复到与准确值相差不大于10%.左波谷:时间位置恢复到相差不多于2个样点时间;幅值,除σ2=0.2 W幅值变小外,其他σ2 噪声条件恢复的幅值都变大,但都不超过0.08.右波谷:时间位置恢复到基本为滞后一个样点;幅值,除σ2=0.2 W 恢复较差外,其余σ2 噪声条件下振幅恢复到不大于0.07.由上述5种物理量以及图 4b 的表现,在噪声强度σ2 不大于0.020 W 时,加权(tanh(r)/r3)SVR 方法具有良好的去噪效果与较理想的稳健性.
|
|
表 3 叠加不同功率高斯噪声下加权SVR去噪结果与奇异点恢复程度比较 Table 3 Comparisons on the denoised results obtained by using the weighted SVR for noisy data with different noise levels |
本节尝试用加权SVR 滤波方法处理实际地震记录,权函数仍选择w(r)=tanh(r)/r3.图 5a是某油田三维地震勘探共炮点记录的一段(1.2~2.5s, 51~110道).记录上随机噪声比较强,主要分布在70~90 道、105~110 道.图 5b 为对图 5a 经加权SVR 滤波处理的结果.

|
图 5 加权SVR方法处理实际地震记录 (a)原始三维共炮点一段记录(12〜2.5 s) (b)加权SVR处理结果;(c)记录中标注A、B、C、D、E五处的个别道记录子波段放大比较. Fig. 5 Experiment on real seismic data by using the weighted SVR (a) Raw common-shot-point record segment; (b) Result obtained by using the weighted SVR;(c) Comparisons on the enlarged wavelets with labels A,B,C,D and E. |
对比图 5a、5b 可见,经滤波后在70~90 道、105~110道上的随机噪声得到有效抑制.此外,以图 5a、b中标注的5处(A、B、C、D、E)记录范围来说明处理前后波形变化.按照通常认识,正常地震子波波峰波谷两侧应该大致对称(即比较“正",尤其主要波峰峰值两侧).在图 5a、b 标注的5 处,未滤波时地震记录主要波峰存在一定程度的畸变,加权滤波后地震子波恢复较好,主要波峰基本不畸变.为更清楚说明这一结果,取出上述5 处的个别道记录子波加以放大进行比较(图 5c).图 5c的5组子波记录都表现出加权处理后子波得到较好的恢复.虽然我们不知道真实地震子波的形态以及在随机噪声背景中受到畸变的子波波形经过处理后应该具有的波形,但按正常的认识,地震子波中可能有一个相位振幅较强(波峰),而其两侧均匀降幅[9],这在图 5c中已得到印证.地震子波形态的恢复,可能包含加权SVR 方法的去噪功能,但也可能包含该方法的良好的稳健性的因素.记录的这种改善可能包含着滤波处理过程的内在的能力,在记录波形前后变化上难以判断,我们只能用前几节的实验与分析去说明加权SVR 具有好的稳健性,在处理地震记录时也必然起一定作用.
5 结论与讨论系统或信号处理过程的影响函数是用于研究过程稳健性的常用数学工具.鉴于在误差函数为最小平方条件下,Ricker子波核LS-SVR 的无界影响函数,进而其稳健性程度差的特性,本文经过仿真实验得到比已有的有效权函数效果更好的权函数(tanh(r)/r5 或tanh(r)/r3).用这一权函数的加权SVR滤波方法处理理论含噪记录和实际地震记录都得到比较理想的结果.这一成果发展了已有的Ricker子波核LS-SVR 方法.
由于本文是对Ricker子波核LS-SVR 滤波方法的稳健性程度的初次研究,必然还存在一些不完善的环节待改进.例如,对实验中所使用的权函数tanh(r)/r3,仅是对原来的权函数tanh(r)/r分母r的改进;分子tanh(r)的自变量r也有可能改变,使新权函数表现出更好的增强稳健性的能力.tanh(r)是实奇函数,而且具有极限
| [1] | Mercer J. Functions of positive and negative type and their connection with the theory of integral equations. Philosophical Transations of the Royal Society of London Series A , 1909, 209: 415-446. DOI:10.1098/rsta.1909.0016 |
| [2] | Aronszajn N. Theory of reproducing kernels. Transactions of the American Mathematical Society , 1950, 68(3): 337-404. DOI:10.1090/S0002-9947-1950-0051437-7 |
| [3] | Aizerman A, Braverman E M, Rozoner L I. Theoretical foundations of the potential function method in pattern recognition learning. Automation and Remote Control , 1964, 25: 821-837. |
| [4] | Vapnik V N. The Nature of Statistical Learning Theory. New York: Springer-Verlag, 1995 . |
| [5] | Sonnenburg S, Rätsch G, Schäfer C, et al. Large scale multiple kernel learning. Journal of Machine Learning Research , 2006, 7: 1531-1565. |
| [6] | 邓小英, 杨顶辉, 刘涛, 等. Ricker子波核支持向量回归的Mercer条件拓展问题研究. 地球物理学报 , 2009, 52(9): 2335–2344. Deng X Y, Yang D H, Liu T, et al. Study on Mercer condition extension of support vector regression based on Ricker wavelet kernel. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2335-2344. |
| [7] | Deng X Y, Yang D H, Xie J. Noise reduction by support vector regression with Ricker wavelet kernel. Journal of Geophysics and Engineering , 2009, 6(3): 177-188. |
| [8] | 邓小英, 杨顶辉, 刘涛, 等. 最小二乘支持向量回归滤波系统性能分析. 地球物理学报 , 2010, 53(8): 2004–2011. Deng X Y, Yang D H, Liu T, et al. Performance analysis of least squares support vector regression filtering system. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 2004-2011. |
| [9] | 杨宝俊. 勘探地震学导论(上). 长春: 吉林科学技术出版社, 1990 . Yang B J. Introduction to Prospecting Seismology (Volume I), (in Chinese). Changchun: Jilin Science & Technogy Press, 1990 . |
| [10] | 张贤达. 现代信号处理. 北京: 清华大学出版社, 2002 . Zhang X D. Modern Signal Processing (in Chinese). Beijing: Tsinghua University Press, 2002 . |
| [11] | Debruyne M, Christmann A, Hubert M, et al. Robustness and stability of reweighted kernel based regression. Technical report, 2006, http://wis.kuleuven.be/stat/ |
| [12] | Christmann A, Steinwart I. Consistency and robustness of kernel-based regression in convex risk minimization. Bernoulli , 2007, 13(3): 799-819. DOI:10.3150/07-BEJ5102 |
| [13] | Dollinger M B, Staudte R G. Influence functions of iteratively reweighted least squares estimators. Journal of the American Statistical Association , 1991, 86: 709-716. DOI:10.1080/01621459.1991.10475099 |
| [14] | Suykens J A K, Brabanter J D, Lukas L, et al. Weighted least squares support vector machines: robustness and sparse approximation. Neurocomputing , 2002, 48(1-4): 85-105. DOI:10.1016/S0925-2312(01)00644-0 |
| [15] | Von Mises R. On the asymptotic distribution of differentiable statistical functions. The Annals of Mathematical Statistics , 1947, 18: 309-348. DOI:10.1214/aoms/1177730385 |
| [16] | Hampel F. The influence curve and its role in robust estimation. J. Amer. Statist. Assoc. , 1974, 69: 383-393. DOI:10.1080/01621459.1974.10482962 |
 2011, Vol. 54
2011, Vol. 54