2. 96165部队,江西乐平 333300;
3. 中科院大气物理研究所大气科学与地球物理流体动力学数值模拟国家重点实验室,北京 100029
2. No. 96165 Troops of PLA, Leping Jiangxi 333300,China;
3. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029,China
Rossby波是地球大气中的一种重要波动,在大气环流演变、数值天气预报和气候预测中都占有重要地位,在中纬度地区,按波长Rossby波可分为两类:一类是天气尺度波;一类是行星尺度波,天气尺度波动的活动和演变直接关系到中纬度地区长波槽脊、大气涡旋等天气系统的演变;而行星尺度的波动是大气低频振荡产生的主要机制.以往对Rossby波的研究多着眼于波动的不稳定性问题,其研究方法也多用标准模法.关于这方面最早的工作是Charney[1]、Eady[2]和Kuo[3]提出的斜压和正压不稳定理论,这开创了地球流体动力学的里程碑.尽管标准模方法有其自身的优点,但该方法只能研究扰动的线性演变,且无法讨论初始扰动大小和形态对其发展的影响,更不能研究扰动在发展过程中形态的演变过程[4~6].而实际天气的发生发展,特别是一些灾害性天气的发展都是在有限时间内,主要是由在有限时段内急剧增长的扰动引起,因此研究和讨论在有限时段内扰动的发展问题,对于从动力学的角度分析这些灾害性天气现象,以便做出准确的预报是十分必要的.有限时间内的扰动增长问题属于动力稳定性问题的研究范畴,但不能用标准模的方法来研究.
对非线性Rossby 波的不稳定理论研究,多采用能量法[7~10],但能量法是从整个系统的角度来讨论大气运动的不稳定问题,对大气演变过程却一无所知.为了寻找大气Rossby波的精确解,Green 函数法[11]、Fourier变换法[12, 13]、Laplace变换法[14, 15]也是研究Rossby 波演变的常用方法.但用这些方法也仅能得到线性Rossby 波的精确解,对非线性Rossby波精确解至今仍是一个没有解决的难题.
为了解决有限时段内扰动的发展问题,应将描写波动的方程作为初值问题求解.但由于真实基流的复杂性,无论是对线性还是非线性的方程进行解析求解都是困难的.随着计算数学和计算机科学的迅猛发展,近年来,利用数值方法[16~19]研究非线性Rossby波的稳定性和波流相互作用等问题已成常规.数值方法的应用,在一定程度上弥补了理论分析的不足,加深了人们对大气Rossby波演变的认识,具有广泛的发展前景.
本文的目的就是研究真实基流情形下,大气非线性Rossby波流场结构和总能量的演变特征.内容分两部分,第一部分针对非线性的准地转正压位涡方程,设计了一个高精度的隐式差分迭代公式,并通过已知Couette流方程的精确解,验证了对线性方程差分格式的稳定性以及数值解的精确性;然后通过构造精确解,修改非线性方程的方法,验证了非线性基流情况下,非线性方程差分格式的稳定性以及数值解的精确性.第二部分利用双Gauss函数拟合出500hPa高度上纬向风随纬度的变化函数,并利用第一部分自行设计的差分格式,数值计算了北半球中纬度地区Rossby波流场结构和总能量随时间的演变,并讨论了初值对Rossby波演变的影响.
2 数学模型及差分格式设计 2.1 数学模型在只考虑x方向存在基本气流U(y)的情况下,描写大气Rossby 波的无量纲准地转正压位涡方程可写为[20]:

|
(1) |
其中ζ = Δψ 为涡度,ψ 为流函数,F=(L/R)2,L为特征水平尺度,R=c0/f为Rossby变形半径,ε 取0和1分别表示方程(1)为线性方程和非线性方程.在区域Ω=[0,Lx]×[0,Ly]中方程(1)的初边值条件为:
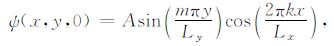
|
(2) |

|
(3) |

|
(4) |
其中Lx,Ly都是无量纲数,(3)和(4)式表示x方向取周期边界条件,y方向取固壁边界条件.定义Rossby波的总能量和相对总能量如下:

|
(5) |
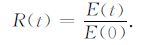
|
(6) |
对方程(1)采用差分方法离散化,空间方向采用蛙跳格式,时间方向采用一阶向后差分,则(1)式的隐式差分方程可写为:
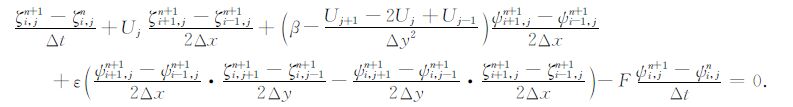
|
(7) |
考虑到流函数与相对涡度的关系为

|
上式可转化为只含流函数ψ 的差分方程表达式.从该格式可以看出计算每一个格点的流函数时,需要用到其周围12 个点的数值,时间积分采用Gauss-Seidel迭代法.
计算出流函数的数值解后,再利用梯形积分公式按(5)和(6)式计算出总能量和相对总能量.
3 差分格式计算精度和稳定性的验证 3.1 Couette流方程精确解与数值解的比较由于描述平面无黏Couette 流方程存在精确解,为了验证差分格式(7)的计算精度和稳定性,取F=0,β=0,ε=0,U(y)=y,这样方程(1)可简化成Couette流方程形式:

|
(8) |
为简单,计算区域在纬向上取Lx=2π,经向上取Ly=1,这样在区域Ω1=[0,2π]×[0,1]上的边值条件(2)~(5)式可写为:
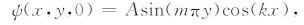
|
(9) |

|
(10) |
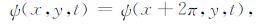
|
(11) |
由文献[11]知,Couette流方程(8)的精确解为:
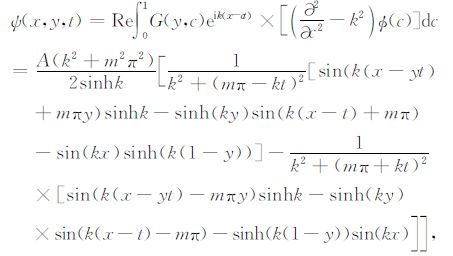
|
(12) |
其中
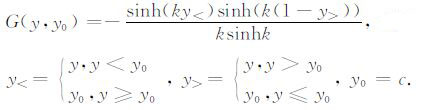
|
(13) |
为了验证差分格式(7)的计算精度和计算稳定性,将Couette流精确解的相对能量与数值解进行比较.数值计算时,将y方向等距剖分为51个格点,使时空步长分别满足Δt=0.1Δx,Δx=Δy,并要求每一时间层的最大迭代误差为eps=10-4.计算中取A=1.0,k=4,m分别为1,2,3,4,计算时间范围为t∈[0,60],m的不同取值表示了不同尺度的初始波动结构,m越大,其波动的经向尺度越小.
图 1显示了四种不同初值条件情形下Couette流精确解和数值解对应的相对能量随时间的演变.
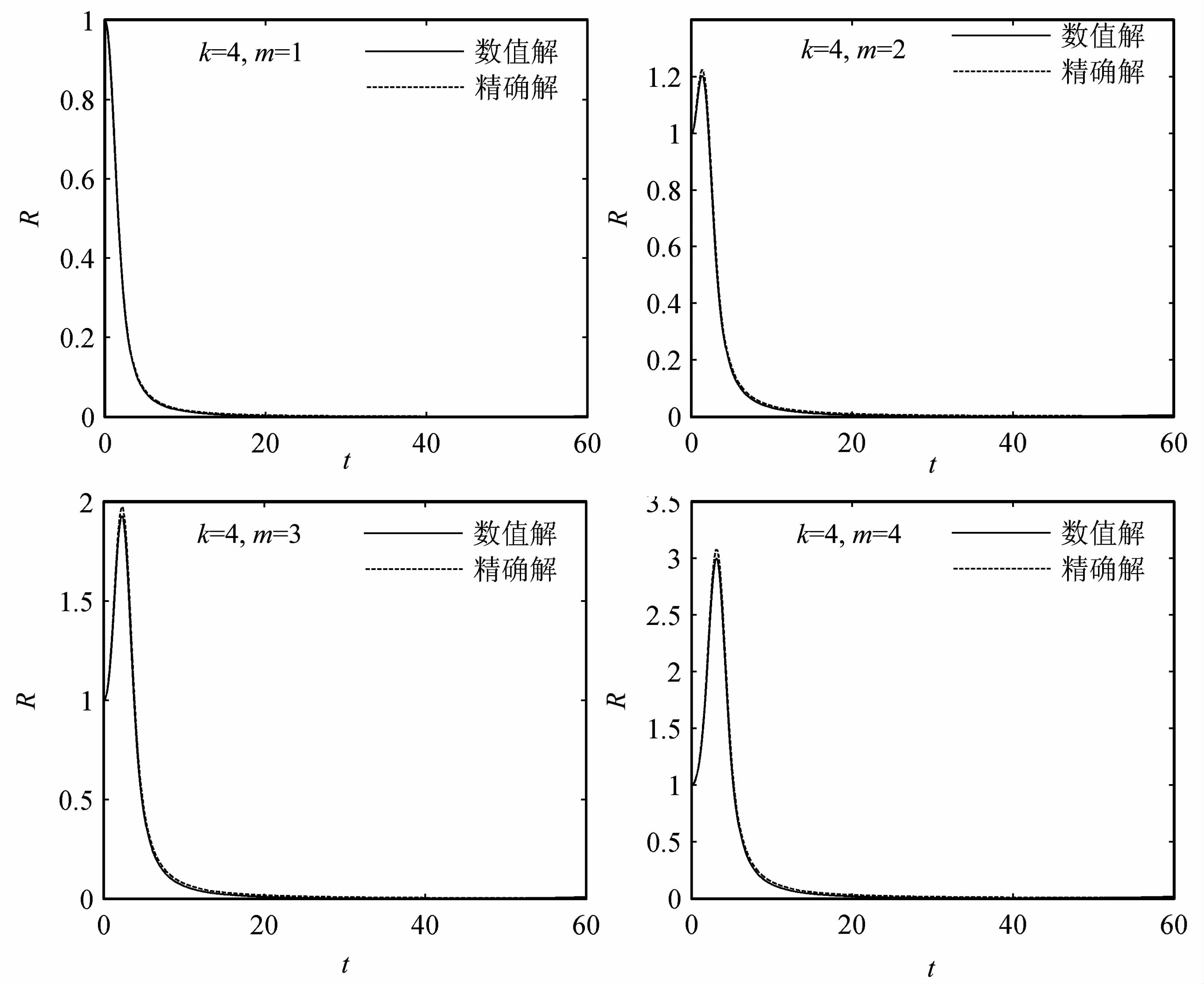
|
图 1 Couette流相对能量的精确解和数值解CR为相对总能量) Fig. 1 The exact solution and numerical solution of Couette flow relative energy |
由图 1可以看出,无论波动的初始空间尺度是大还是小,利用差分格式(7)都可以很好地模拟出Couette流能量随时间的演变,在整个计算过程中,数值解与解析解的能量同步变化,达到最大值的时间也完全相同,没有出现计算不稳定现象和由于计算累积误差所导致能量振荡现象.若定义数值解的相对误差为数值解与精确解之差与精确解之比,当k=4,m取不同值时,Couette流数值解的相对误差如表 1,由表可见,随m的增大,即初始波动经向尺度减小,数值解与精确解之间的误差也增大,但如果增加计算区域内的分辨率,这种误差就会相应地减小.这说明数值求解空间尺度较小的波动时,必须用高分辨率的数值离散化格式,这样才能对较小尺度的波动进行更精确的描述.
|
|
表 1 k=4时 Couette 流数值解的相对误差(%) Table 1 The relative error of Couette flow numerical solution in k = 4 |
以上与Couette流精确解的比较,只能说明在特殊情况下对线性方程而言差分格式(7)的计算精度和稳定性,但当方程为非线性时,非线性项是否会带来计算不稳定或计算误差? 这也是研究非线性Rossby波必须考虑的问题.对于非线性方程由于不能求出其精确解,故我们首先通过改写波动方程构造精确解,然后通过比较构造的精确解与改写的波动方程数值解来验证差分格式对非线性方程的计算精度.为了方便构造精确解,将方程(1)改写成如下形式:

|
(14) |
Q是未知函数,为简单,在纬向上取1 波,即k=1,经向上取半波,即m=1,计算区域仍为Ω2=[0,2π]×[0,π],这时方程(14)对应的初边值条件为:

|
(15) |

|
(16) |

|
(17) |
设方程(14)满足以上初边值条件的精确解为:
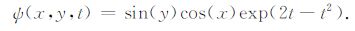
|
(18) |
带入方程(14)后,可知式中Q应有如下形式:
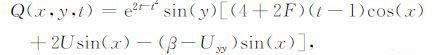
|
(19) |
那么(18)式就是方程(14)的精确解,其中(14)式中的Q必须满足(19)式.为了检验差分格式(7)对非线性方程求解的精度,用格式(7)求解方程组(14),并将得到的数值解与精确解(18)进行比较.为简单,计算时取基流为U=y2+y,F=1,β=2,每一时间层的最大迭代误差为eps=10-4,Δt=0.01Δx,试验采用如下两种不同的方案.
方案1:纬向等距剖分为21 个格点,经向步长为纬向步长的一半;
方案2:纬向等距剖分为41 个格点,经向步长与纬向步长相等.
图 2(a, b)分别显示了方案1 和方案2 情形下的数值解与精确解的相对总能量随时间的演变.

|
图 2 (a)方案一情形下精确解和数值解相对总能量,(b)方案二情形下精确解和数值解相对总能量. Fig. 2 (a) The exact solution and numerical solution of relative energy in case 1,(b) The exact solution and numerical solution of relative energy in case 2 |
从图 2可以看出,无论方案1还是方案2,数值解相对总能量与精确解相对总能量同步变化,且达到最大值的时间也相同,但二者的最大值存在相对误差,方案1的相对误差为4.03%,方案2为0.96%.这说明随着纬向格点数的增加,计算解更接近于精确解.
综上可见,无论是对线性方程还是非线性方程,差分格式(7)都具有很好的计算精度和稳定性,特别是随着网格分辨率的增大,计算精度增大.所以可以用它来数值研究真实基流情形下的大气非线性Rossby波的演变.
4 结论为了研究北半球不同季节真实基流情形下线性和非线性Rossby波演变特征,首先针对β 平面上准地转正压位涡方程定义了Rossby波的总能量和相对总能量;其次,设计了一个空间方向等间距的高精度隐式差分格式,并利用Couette流的精确解验证了线性方程情形下差分格式的精度和稳定性;对非线性方程通过改变方程并构造精确解的方法,验证了其差分格式的计算精度和稳定性.结果发现,不论是对线性方程还是非线性方程,该差分格式数值计算出的相对总能量与它们精确解的相对总能量之间的相对误差都很小,可以很好地模拟波动的演变过程.这些工作为研究真实基流情况下非线性Rossby 波的演变提供了有用的工具.在本文的第二部分,将利用ECMWF46年的500hPa高度场上纬向风再分析资料,利用双Gauss函数拟合纬向平均基本气流的气候场,利用以上给出的高精度差分格式讨论了真实基流下Rossby 波的能量演变及初值的影响.
| [1] | Charney J G. The dynamics of long waves in a baroclinic westerly current. J Meteor , 1947, 4: 135-162. |
| [2] | Eady E T. Long wave and cyclone waves. Tellus , 1949, 1: 33-52. DOI:10.1111/tus.1949.1.issue-3 |
| [3] | Kuo H L. Dynamic instability of two-dimensional non-divergent flow in a barotropic atmosphere. J Meteor , 1949, 6: 105-122. DOI:10.1175/1520-0469(1949)006<0105:DIOTDN>2.0.CO;2 |
| [4] | Pedlosky J. An initial value problem in the theory of baroclinic instability. Tellus , 1964, 16: 12-17. DOI:10.1111/tus.1964.16.issue-1 |
| [5] | Burger A P. Instability associated with the continuous spectrum in a baroclinic flow. J Atmos Sci , 1966, 23: 272-277. DOI:10.1175/1520-0469(1966)023<0272:IAWTCS>2.0.CO;2 |
| [6] | Tung K K. Initial-value problems for Rossby waves in a shear flow with critical level. J Fluid Mech , 1983, 133: 443-469. DOI:10.1017/S0022112083002001 |
| [7] | Andrews D G. On the existence of nonzonal flows satisfying sufficient conditions for stability. Geophys Astrophys Fluid Dyn , 1984, 28: 243-257. DOI:10.1080/03091928408230366 |
| [8] | Salmon R. Hamiltonian fluid mechanics. Ann Rev Fluid Mech , 1988, 20: 225-257. DOI:10.1146/annurev.fl.20.010188.001301 |
| [9] | Zeng Q C. Variational principle of instability of atmospheric motions. Adv.Atmos. Sci. , 1989, 6: 137-172. DOI:10.1007/BF02658013 |
| [10] | Mu M. Nonlinear stability theorem of two-dimensional quasi-geostrophic motions. Geophys Astrophys Fluid Dyn , 1992, 65: 57-77. DOI:10.1080/03091929208225239 |
| [11] | Farrell B F. The initial growth of disturbances in a baroclinic flow. J Atmos Sci , 1982, 39: 1663-1687. DOI:10.1175/1520-0469(1982)039<1663:TIGODI>2.0.CO;2 |
| [12] | Yamagata T. On the propagation of Rossby waves in a weak shear. J Met Soc Japan , 1976, 54: 126-128. |
| [13] | 张亮, 张立凤, 吴海燕, 等. 正压Rossby波扰动能量. 物理学报 , 2010, 59(1): 44–53. Zhang L, Zhang L F, Wu H Y, et al. The disturbance energy of barotropic Rossby wave. Acta Phys Sin (in Chinese) , 2010, 59(1): 44-53. |
| [14] | Béland M, Warn T. The radiation condition for transient Rossby waves. J Atmos Sci , 1975, 32(10): 1873-1880. DOI:10.1175/1520-0469(1975)032<1873:TRCFTR>2.0.CO;2 |
| [15] | Achterberg R K, Ingersoll A P. Numerical simulation of baroclinic Jovian vortices. J Atmos Sci , 1994, 51: 541-562. DOI:10.1175/1520-0469(1994)051<0541:NSOBJV>2.0.CO;2 |
| [16] | Majda A J, Biello J A. The nonlinear interaction of barotropic and equatorial baroclinic Rossby waves. J Atmos Sci , 2003, 60: 1809-1821. DOI:10.1175/1520-0469(2003)060<1809:TNIOBA>2.0.CO;2 |
| [17] | Lyman J M. Tropical instability waves as a resonance between equatorial Rossby waves. J Phys Oceanogr , 2005, 35: 232-254. DOI:10.1175/JPO-2668.1 |
| [18] | Zhang L, Huang S X, Zhang L F.. Numerical experiments about growth of disturbance energy of potential vorticity equation within finite time scope. Proceedings of the 5th International Conference on Nonlinear Mechanics (ICNM-V). Shanghai University Press , 2007: 1195-1200. |
| [19] | Lu C, Byod J P. Rossby wave ray tracing in a barotropic divergent atmosphere. J Atmos Sci , 2008, 65: 1679-1691. DOI:10.1175/2007JAS2537.1 |
| [20] | 余志豪, 杨大升, 贺海晏, 等. 地球物理流体动力学. 北京: 气象出版社, 1995 . |
| [22] | Yu Z H, Yang D S, He H Y, et al. Geophysics Hydrokinetics. Beijing: China Meteorological Press, 1995 . |
 2011, Vol. 54
2011, Vol. 54


