2. 国土资源部 应用地球物理综合解释理论开放实验室,长春 130026
2. Laboratory for Integrated Geophysical Interpretation Theory of Ministry for Land and Resources, Changchun 130026, China
在直流电法勘探中,地形的起伏对电阻率法有着重要的影响[1~3].经常出现因地形引起的高阻或低阻干扰,因此必须对地形影响进行评估校正.早期采用物理模拟的方法,但存在成本、模拟介质匹配、尺度等问题.而后的角域地形理论计算[4]和保角变换[5],虽然可以得到理论上的解析解,但其适应的地形特殊而有限,无法适用于工程应用中,且保角变换一般只适用于二维情况.目前采用数值模拟的方法取得了一定的进展,国内外专家在此方面做了不少的研究工作.数值方法主要有边界元法,有限元法和有限差分法[6~27].边界元法对特定的模型有较好的效果,但面对复杂模型和多异常体时,因格林函数求取相对困难,因此并不具有优势.现阶段国内的研究相对较集中于有限元法[12~15],有限元法灵活的网格剖分能较好地逼近地表形状,但其存在网格剖分复杂、计算量大等固有的缺陷.而有限差分法相对有限元法具有网格剖分简单、计算量较小、易于编程实现等特点,因此如果让有限差分法也同样具有较好的处理曲边界的能力,那数值模拟将变得更为简单.但国内外有限差分法直流电场数值模拟多基于水平地表,国内也仅有罗延钟采用有限体积法对起伏地表进行过研究[11].然而采用有限差分法对曲边界的处理在地震勘探、流体力学和数值热传导等领域中相对较为成熟[28~30],因此可以借鉴这些学科领域中的研究成果来解决起伏地表下直流电场数值模拟问题.直流电场基本方程属于椭圆方程的范畴,在一般教科书中,任意边界情况下的椭圆方程黎曼边界条件问题(导数型边界条件)多采用转移法[31],但转移法实际上修改了地形形状,在数值计算前就已人为地引入了误差.为了避免这个问题,本文在非正则内点上使用不等距差分的基础上,在曲边界上直接应用边界条件,这样很好地解决了转移法修改地形形状的问题.
三维有限差分存在计算量大的问题,特别是二极、三极、四极等装置计算视电阻率时需要计算不同位置供电点的电位场,这样无论采用直接法还是迭代法解最后的线性方程组,计算量都相当大.因为采用迭代法,有n个供电点就需要计算n次线性方程组,而每次线性方程组的计算量还依赖于网格节点的数量,节点越多计算量越大;而如果采用直接法,虽然解线性方程组时通过近似处理,n个供电点只需要分解一次线性方程的系数矩阵,看似节省了计算量,但由于是三维问题,节点数往往很多,这样直接法的系数矩阵分解的计算量和存储量是惊人的.因此在现有的求解大型线性方程组算法的基础上,减少网格节点数是节省计算量的最好办法.对于其中一维电性参数保持不变的三维模型,经过简化最终可把三维的方程简化为若干个波数对应的二维方程,这就是常说的2.5维,这样减少一维相当减少网格节点数,降低了计算成本.而在电法勘探中沿垂直测线方向电性参数基本保持不变的构造是存在的,这也是在理论上研究2.5维情况的重要原因.
2 基本方程电位基本方程为:

|
(1) |
其中

|
(2) |
r在三维时表示坐标向量(x,y,z),在二维时表示坐标向量(x,z),r0 为电源位置,σ 为电导率,U为电位,I为电流,δ为迪拉克函数.为了提高求解方程的精度,采用背景场加异常场的思想(在此的背景场加异常场的思想与常规的背景场加异常场的思想略有不同,关于这一点在下一小节中有具体阐述).因此电位和电导率可写成以下形式:
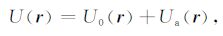
|
(3) |
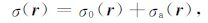
|
(4) |
U0(r)为背景电场,Ua(r)为异常电场,σ0(r)为背景电导率,σa(r)为异常电导率.U0(r)在此采用全空间线/点电源场,2维为:

|
(5) |
2.5维为:
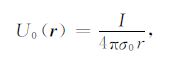
|
(6) |
其中r为向量r到电源r0 的距离.把式(3)、(4)代入(1)然后减去背景场所满足的方程
Δ·[σ0(r) ΔU0(r)]=f(r),
可得异常场2维方程:
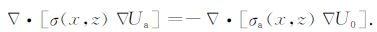
|
(7) |
对于2.5维,采用余弦傅氏变换,经过一系列推导可得:
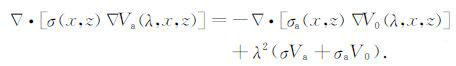
|
(8) |
式中λ 为波数,Va(λ,x,z)为Ua(x,y,z)的一维余弦傅氏变换,V0(λ,x,z)为式(6)的余弦傅氏变换,其表达式为:

|
(9) |
其中K0(λ,x,z)为零阶修正贝塞尔函数.给定若干个λ 值分别按式(8)求解Va(λ,x,y,z),然后对Va(λ,x,y,z)按照下式作反余弦傅氏变换可计算异常电位值Ua(x,y,z).
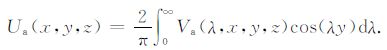
|
(10) |
再利用式(3)就可以计算出总电位场.关于λ 的取值请参看文献[32].由于方程(7)和(8)方程采用五点差分格式离散后的矩阵系数形式相近(可参考文献[11]),因此2.5维关于单个λ 的计算和2维的计算过程几乎一样,只是2.5 维最后比2 维多一个反余弦傅氏变换,所以以下的网格剖分和方程离散都以2维为例.
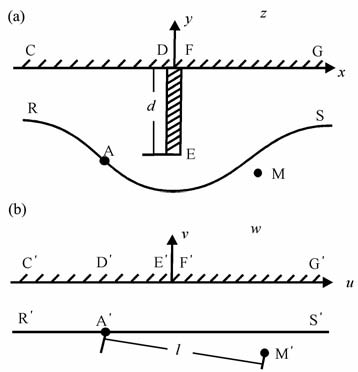
2.1 背景场加异常场的说明本文中采用的背景场加异常场的思想和传统的背景场加异常场的思想略有不同.传统的背景场加异常场的思想是基于水平地表下存在异常体的模型,认为背景场是均匀电导率下产生的半空间电位场.而异常场是电导率异常产生的二次场.本文中的背景场加异常场的思想是把地形看作是一种异常,而背景场采用全空间的均匀电位场.至于为何把地形看作异常而背景场采用全空间均匀电位场,这一想法来源于线源水平地表均匀电导率下电位场公式的推导.如图 1 利用镜像原理可得M点处的电位表达式:

|
(11) |

|
图 1 半空间电位场求解示意图 Fig. 1 Sketch of half-space potential field solver |
其中r为电源A到观测点M之间的距离,r* 为电源A的镜像点A* 到观测点M的距离.根据(11)式,把右边第一项看作是均匀电导率下的全空间背景场,而右边第二项看作是由于地表存在引起的异常场.换句话说,在均匀电导率下原本线源产生的电位场就应该是全空间的,但由于地形的存在使全空间丢失一半变成了半空间,丢失的半个空间自然要引起电位的异常,也就是这里所指的地形引起的电位异常.从均匀电导率的水平地表自然可以推广到均匀电导率的起伏地表.在起伏地表情况下地下M点的电位场依然可以写成上述相同的形式:

|
(12) |
右边第一项依旧是均匀电导率下的全空间背景场,而右边第二项则看作是起伏地表所引起的异常.对于非均匀电导率下的起伏地表情况,地下M点的电位场还是可以写成上述形式,右边第一项还是均匀电导率下的全空间背景场,而右边第二项则看作是起伏地表和电导率不均匀所引起的异常场.
当然背景场取全空间场而非半空间场也是无奈之举,因为地表起伏时没有半空间场的解析表达式,不像传统的背景场加异常场情况中地表是水平的,可以很容易地得到半空间的表达式.而且引入全空间背景场还有一点不利之处是镜像源附近的误差没法很好地降低.传统的背景场加异常场思想采用半空间的背景场主要目的就是为了消除场源附近的误差.这是因为采用半空间背景场后,异常场在源附近就成了缓变场,因此能提高源附近的计算精度.而当背景场采用全空间时,以水平地表为例,此时的异常场实际上成了镜像源的全空间场,因此异常场在靠近镜像源的位置误差自然就大,因为在镜像源附近场不是按线性规律分布,而有限差分的前提是场局部分布为线性近似.既然这样,那为何还要采用背景场加异常场的思想而不直接计算总场,是因为虽然不能像传统的背景场加异常场思想一样完全地消除源附近的误差,但由于采用了解析的全空间场,异常场相当只近似计算了一半的总场,故也能提高近一倍的精度.
3 网格剖分对曲边界问题常采用的是曲网格,特别是正交的贴体网格,对更复杂的边界采用非结构化网格,然而网格的质量会随着边界的复杂程度而明显降低.在网格生成过程中需要花费一定量的计算时间和记录网格节点位置的存储空间,而且网格的生成依赖边界形状,给定一个边界形状就需要一个网格生成过程,其中的繁琐不言而喻.采用笛卡尔网格(矩形网格)简化了网格剖分过程,在起伏地表及以下空间用固定步长的笛卡尔网格进行网格化,如图 2所示.生成的网格节点可以分为以下几种:地表边界点(三角形),即地表边界和网格竖线的交点;计算域边界点(正方形),即人为规定的计算区域上的边界节点,如图 2中的左右和下边界点;非正则内点(五角星),即临近节点四周包含地表边界点的节点;正则内点(圆),即临近节点四周不包含地表边界点的节点.这样的笛卡尔网格剖分不依赖边界的几何形状,且只需要对地表边界点的坐标进行储存,其他类型节点可不储存.但问题也随之而来,曲网格虽然网格生成较为复杂,但对复杂边界有较强的适应能力,而笛卡尔网格对边界的处理能力就较为有限,因此如何提高笛卡尔网格对处理复杂边界的能力正是本文的重点所在.

|
图 2 网格剖分中的节点类型 Fig. 2 Node types in mesh |
按已剖分好的笛卡尔网格对方程进行离散,不同类型的节点有不同的差分格式.正则内点的差分形式采用五点差分格式[11]:

|
(13) |
式中Ui,ja(i,j=1,2,…,n)为节点处的异常场电位值,Ui,j0(i,j=1,2,…,n)为节点处背景场电位值,ai,j、ai,ja(i,j=1,2,…,n)为系数项,其表达式为:
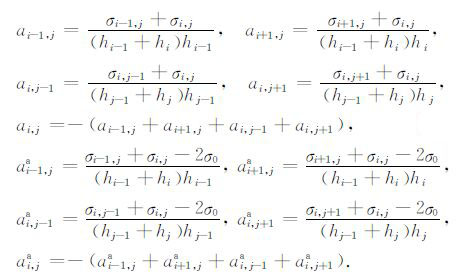
|
(14) |
式中hi(i=1,2,…,n)和hj(j=1,2,…,n)为水平方向和垂直方向节点间距.2.5 维时除系数ai,j和ai,ja有些变化,其他系数均与2维时相同.
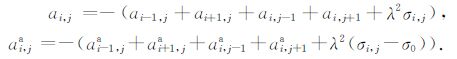
|
(15) |
一般正则内点的五点差分格式为等距差分,且在网格剖分中常采用Δx= Δz=h.对于非正则内点由于其四周包含地表边界点,此时网格间距不再等长,如图 3所示h1 ≤h,h2 ≤h,但仍可以采用五点差分格式,只不过变为不等距差分[30].不等距差分当h1 →0或h2 →0时(14)式中部分系数项会趋于∞,这样会使数值计算不稳定.一种简单的处理办法是给定一个阀门值ε,当间距小于ε时认为地表边界节点和网格节点重合,这样非正则内点往内移动一格,差分格式中的系数就会避免出现趋于∞ 的情况.对于非正则内点的不等距差分格式中含有地表边界和水平网格线相交的节点(图 3 中的R 点)有两种处理办法.方法一,这种节点纳入地表边界点的范围内,其作为数值计算的节点之一,该点的差分格式按地表边界节点的差分格式建立.只是这样处理网格剖分相对繁琐,需要记录该点的位置,而且使得原本简单的索引规律变得复杂.但这样处理也有益处,增加了地表边界节点的数目,在地表边界处更能控制住边界条件.方法二,地表边界节点只考虑网格竖线与地表边界的交点,网格水平线与地表边界的交点不作为计算点.当非正则内点五点不等距差分格式用到此节点时,此节点的值用附近的节点插值来表示.例如图 3所示R 点处的值用P 点和S点插值得到的T 点来近似代替.这种方法网格剖分相对简单,编程时节点索引较为简洁.本文按后一种方法进行处理.

|
图 3 非正则内点示意图 Fig. 3 Node types in mesh |
对于计算域边界由于一般距离源和异常体较远,因此在计算域边界上的总场直接取背景电导率下的半空间场
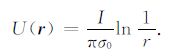
|
(16) |
这只是一种近似处理,在计算域边界远离源和异常体时是可以成立的.当计算域边界上有了总场的值,自然就可以推得异常场在计算域边界上的表达.根据式(3)、(5)、(16)可得:

|
(17) |
此式为异常场在计算域边界上的狄利克雷表达式.
2.5维情况下同样可得:

|
(18) |
其中K0(·)为零阶修正贝塞尔函数.
4.4 地表边界点由于采用背景场加异常场的思想,地表边界节点,原本总场法向导数等于零的边界条件变换成以下形式:

|
(19) |
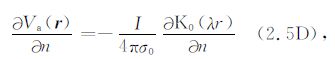
|
(20) |
θ 是r与边界法线方向n的夹角.为了离散式(19)、(20),可在地表边界点处对Ua 或Va 进行一阶或二阶精度Taylor展开:
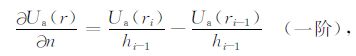
|
(21) |
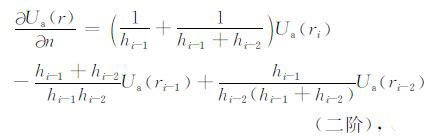
|
(22) |
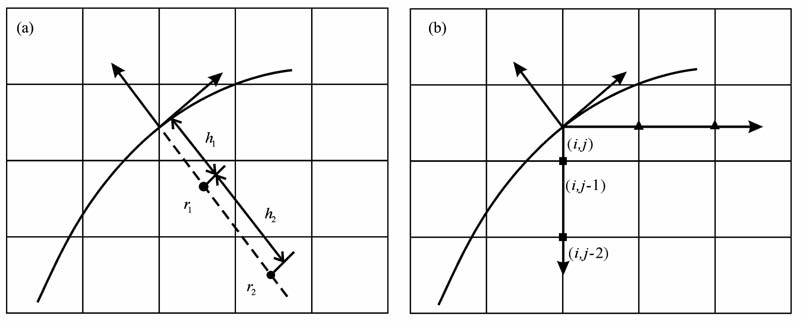
其中ri(i=1,2,…,n)为离散点系,hi(i=1,2,…,n)为点系间的距离,如图 4a 所示.关于点Ua(r1)和Ua(R2)的值可以通过其周围节点采用双线性插值获得,值得注意的是距离h1 的选取,如果距离过于接近边界,点r1 周围四个点(网格节点)有可能超出了边界,这样的计算点根本就不存在,双线性插值时自然会给出错误的信息.为了避免这个问题,可通过控制h1 来实现.当h1 ≥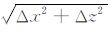
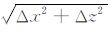
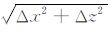
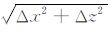
|
图 4 (a)法线方向直接求导;(b)水平方向和垂直方向分别求导 Fig. 4 (a) Direct derivate by normal direction; (b) Horizontal and vertical respectively derivate |
以上是采用Taylor展开的离散形式直接求取边界上的法向导数[34~36],除此之外法向导数还可以通过分别求取x方向和z方向上导数来获得[34].如图 4b,z方向上的导数可通过边界点(i,j)和内部节点(i,j-1)、(i,j-2)二阶Taylor展开求取.x方向上也是同样如此,只是x方向上的以三角形表示的点并非网格节点,不过可以容易地采用一维线性插值求得.对于计算z方向导数同样存在不等距差分格式中的问题,需要设置阀门值避免(i,j)和(i,j-1)距离过小引起计算的不稳定,而x方向导数就不存在这种问题,因为其间距为水平网格间距Δx.有了x方向导数和z方向导数,在此以Gx和Gz表示,则有法向导数,
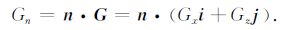
|
(23) |
Gn为法向导数,G为梯度,n为法线向量,法线向量可根据实际采样的地表边界高程数据通过三次样条插值获得.对地表边界点的处理本文采用第一种方法.
5 电源位置的处理对基本方程离散后可以采用很多数值方法来求解这一线性方程组,在此本文采用松驰迭代法.但在进行迭代求解之前还必须解决电源位置的问题,因为观察地表边界点的公式(19)、(20)不难看出其含有地表点到电源的距离r,而当电源位于地表时,此电源点又是地表边界点,r=0使得式(19)中的1/r和式(20)中的K0 变成无穷大,从而使数值计算无法继续进行.一种简单的办法是使电源从地表下移一段距离.当然为了更好地近似模拟电源在地表时的情形,下移的距离应尽量小,不过这种下移也有其合理性,因为实际电法勘探中电源电极都是插入地表一定深度的,也就是说电源不是严格在地表上的.还有一种方法就是电源放置在地表但不能放置在地表边界节点上,这样也同样可避免r=0的情况.但这样,靠近电源的地表边界点由于r过小导致式(19)中的1/r和式(20)中的K0 过大,会不会引起数值计算问题需进一步考虑,当然如果水平网格距离选取的一定大,把电源放置在两个地表边界点的中间应能很好地解决这一问题.在本文中为更好地和实际电法勘探情况相符,采用电源下移几个网格的办法.
6 算法验证本文通过两种思路来验证该方法的有效性.第一种:该方法是基于起伏地表边界提出来的,那自然也适用水平地表情形,而地表为水平时是存在解析解的,这样就给该方法提供了一个很好的评判依据.
模型:电导率σ=1S/m, 电流I=1A,网格间距水平和深度方向各自为Δx=Δz=1m, 模型大小为99m×119m.图 5a为2维数值解与解析解的相对误差,线源位置(50m, -10m).图 5b是2.5维数值解与解析解的相对误差,点源位置(50m, -10m).从以上两图不难看出该方法的电场数值模拟是可行的.

|
图 5 (a)2D 电位精度;(b)2.5D 电位精度 Fig. 5 (a) 2D accuracy of potential; (b) 2.5Daccuracyofpotential |
在背景场加异常场的说明一节中已做过阐述,当地表水平时,计算的异常场实际就是镜像源的全空间场,其误差分布应是在靠近镜像源的位置最大,这似乎与图 5a和5b中显示的有所差别.这主要是有两个原因引起的:一是在实际的计算过程中计算域边界条件中的距离采用的是边界到源的距离而非精确的边界到镜像源的距离,因为当地表起伏时镜像源很难找到,也就是说计算域边界本身有一定误差.关于这一点可从图 5a和5b右上角和左上角位置误差较小得到应证,因为在这两处到源和镜像源的距离是相等的;二是图 5a和5b是总场误差图而非异常场误差图.图 5a和图 5b误差分布略有不同是因为2维和2.5维电位场效应不同所致.
另一种评判的方法是起伏地表下的数值解直接与起伏地表下的解析解进行对比,这种评判方法最为理想,然而起伏地表下的解析解很难求解,这也正是为什么采用第一种评判标准的原因.值得庆幸的是,根据保角变换原理可以获得个别特殊起伏地形的解析解,但只限于2维情况,2.5维和3维无法实现.
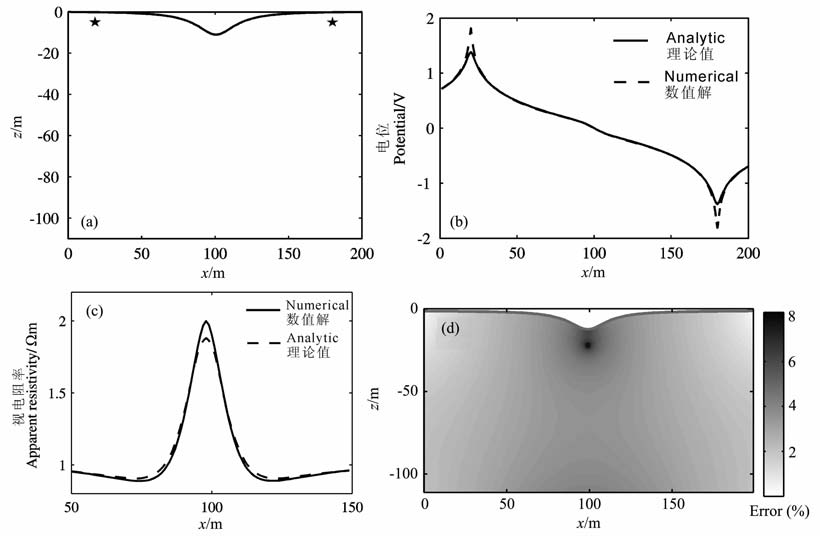
保角变换原理参见附录A,模型参数取v=-12,d= 20.有限差分数值计算中Δx= Δz=1m, I=1A,σ=1S/m, 模型大小为199m×111m.图 6a为2D 地形图,星号为正电极源(19 m, -2 m)和负电极源(179m, -2m)位置.图 6b为该模型地表电位有限差分数值解与保角变换理论解的对比.图 6c为该模型地表视电阻率有限差分数值解与保角变换理论解的对比,视电阻率的计算采用的是中间梯度装置,测量电极MN=2m.图 6d为单正电极线源时地下总电位场的误差图,正电极源位置为(99m, -21m).
|
图 6 (a)2D 地形图;(b)2D 地表电位数值解与解析解的对比;(c)2D 视电阻率数值解与解析解的对比;(d)2D 单正电极源整个计算区域的电位误差 Fig. 6 (a) Topographic diagram; (b) The surface potential numerical comparison with the analytic solution; (c) Numerical solution of the apparent resistivity contrast with the analytic solution; (d) Potential error of the entire tield about single positive source |
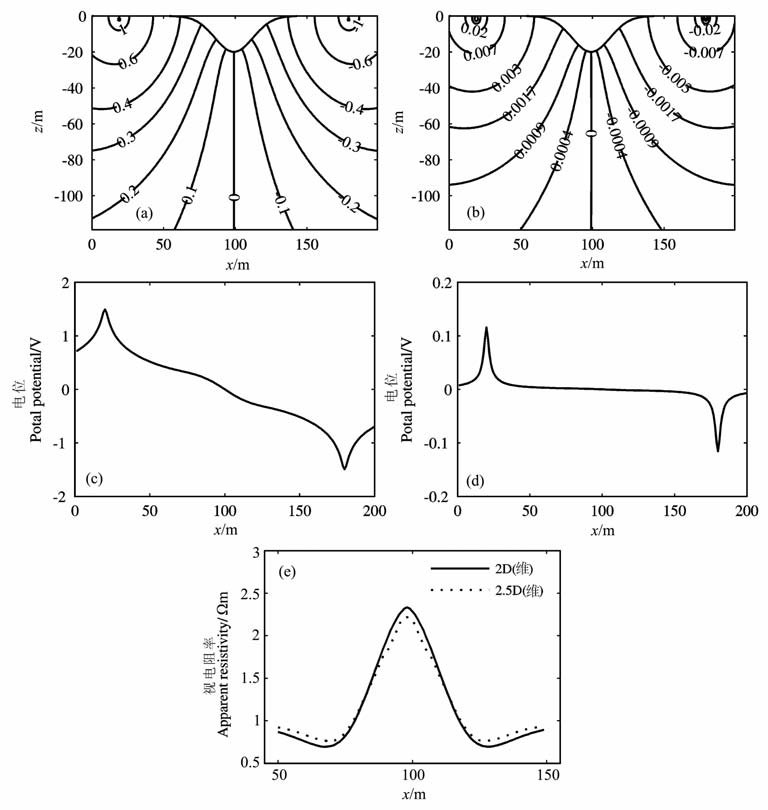
实例1:山谷模型中间梯度装置2D和2.5D对比.山谷模型的高程数据由函数z=-20exp(-0.0009πx2)产生,电导率σ=1S/m, 电流强度I=1A,网格间距水平和深度方向各自为Δx=Δz=1m, 模型大小为199m×119m, 正电极源(19 m, -2 m),负电极源(179m, -2m).图 7a、图 7b分别为2 维和2.5 维山谷模型电场的分布,电位线与地表垂直满足了电位在地表处法向导数为零的边界条件,从这一点来说,该例子的数值模拟结果是可信的.图 7c、图 7d分别为2维和2.5 维山谷模型地表处的电位分布.图 7e为中间梯度装置,MN=2 m 时2维和2.5维的视电阻率,两者的视电阻率基本吻合,这从另一侧面也反映了本方法的有效性.视电阻率在山谷出现高阻异常符合山谷地形与视电阻率呈镜像对称的规律.
|
图 7 (a)2D 电场分布;(b)2.5D 电场分布;(c)2D 地表电位值;(d)2.5D 地表电位值;(e)2D 和2.5D 视电阻率的对比 Fig. 7 (a) 2D electric field distribution; (b) 2.5D electric field distribution; (c) 2D surface potential value;(d) 2.5Dsurface potential value; (e) 2D and 2.5D apparent resistivity comparison |
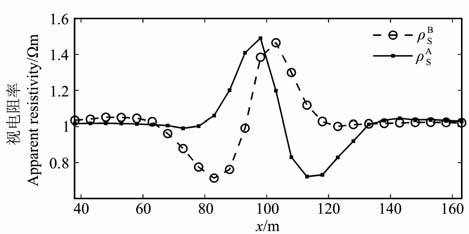
实例2:2D 山谷模型联合剖面装置视电阻率计算.山谷模型与图 6a中的一致,联合剖面装置AO=18m, BO=18m, MN=8m.图 8为山谷模型的联合剖面视电阻率图,在谷底出现高阻正交点[37, 38].
|
图 8 2D 山谷模型联合剖面视电阻率图 Fig. 8 Valley model combined profiles of apparent resistivity |
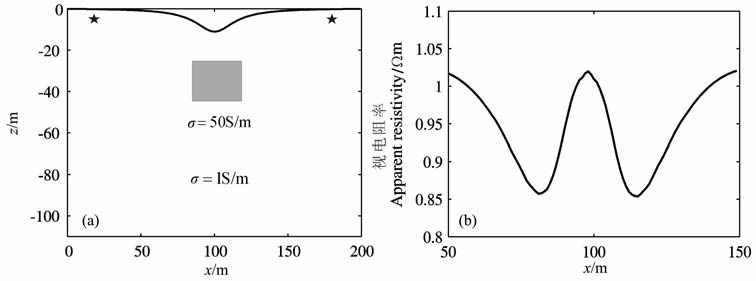
实例3:含有低阻体的2D 山谷模型,中间梯度装置视电阻率计算.在山谷模型下有一矩形低阻体,如图 9a低阻体的电导率σ=50S/m, 其周围的电导率为σ=1S/m, 低阻体所在位置为85m≤x≤113m, -45m≤z≤-26m, 其余参数与图 6a中的一致.图 9b为中间梯度装置的视电阻率曲线,从曲线形态看根本无法反映出地下的低阻异常,这是山谷地形自身的高阻异常掩盖了地下低阻体的信息,使视电阻率曲线产生了畸变.不过曲线形态与装置系数和低阻体埋深等也有关系.
|
图 9 (a)2D 含低阻体的山谷模型;(b)2D 山谷模型含低阻体的中间梯度视电阻率 Fig. 9 (a) The 2D valley model contains the conductive body;(b) Intermediate gradient apparent resistivity of 2D val 1 ey model contained the conductive body |
本文提出的在非正则内点上采用不等距差分,边界上直接使用导数型边界条件的有限差分数值模拟方法克服了转移法的人为修改边界的弊端,原理上简单明了且易于实现.通过2 维和2.5 维对水平地表的数值解与解析解的验证以及2维情况下采用保角变换直接对起伏地表下数值解和解析解的对比,说明该方法的精度适合于计算要求.山谷模型的数值模拟结果表明其等位线垂直地表也充分符合了地表处的电位法向导数等于零的边界条件.视电阻率表现为地形的镜像对称,山谷模型联合剖面视电阻率出现高阻正交点,也符合已发表的有关文献所阐述的地形对视电阻率的影响规律.这种基于简单的笛卡尔网格剖分来解决起伏地表下的有限差分电场数值模拟不失为一种有前途的方法.
附录 保角变换原理
取变换函数w = 


|
(A1) |
式中x的正负号同u;y的正负号同v.
有了以上的变换函数和其导出的x、y同u、v的关系式,我们可以给定一个d和v,如附图 1b中的直线R′S′,通过关系式(A1)可以在z平面上得到 RS曲线(附图 1a).这样就相当于把附图 1a中z平面上曲边界RS及其下部变换成了附图 1b中w平面上水平边界R′S′及其下部.同时附图 1a中电源A变换成了附图 1b中的A′,观测点M 变换成了M′.而在w平面中M′的电位函数我们可以轻易地得到,其表达式为:
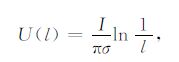
|
(A2) |
其中l为观测点M′到源A′的距离.如果电源A′在水平边界R′S′以下则可利用镜像法得到电位表达式,这样就可计算z平面中曲边界RS 及其下部的所有电位值[5, 39].
|
图 附图 1 z平面变换到w平面示意图 Fig. 附图 1 Diagram of z plane transform to the w plane |
| [1] | Fox R C, Hohmann G W, Killpack T J, et al. Topographic effects in resistivity and induced-polarization surveys. Geophysics , 1980, 45: 57-93. |
| [2] | Truman H T, George R J. Three-dimensional terrain corrections in resistivity surveys. Geophysics , 1984, 49(4): 439-452. DOI:10.1190/1.1441679 |
| [3] | 吴小平. 非平坦地形条件下电阻率三维反演. 地球物理学报 , 2005, 48(4): 932–936. Wu X P. 3-D resistivity inversion under the condition of uneven terrain. Chinese J. Geophys. (in Chinese) , 2005, 48(4): 932-936. |
| [4] | 张赛珍, 王庆乙, 罗延钟. 中国电法勘探发展概括. 地球物理学报 , 1994, 37(Suppl.1): 408–424. Zhang S Z, Wang Q Y, Luo Y Z. An overview on the development of the electrical prospecting method in China. Chinese J. Geophys. (in Chinese) , 1994, 37(Suppl.1): 408-424. |
| [5] | 徐世浙, 王柏钧. 保角变换在电法勘探中的应用. 北京: 地质出版社, 1977 . Xu S Z, Wang B J. Applying of Conformal Transformation in the Electrical Exploration (in Chinese). Beijing: Geological Publishing House, 1977 . |
| [6] | 孙建国. 复杂地表条件下地球物理场数值模拟方法评述. 世界地质 , 2007, 26(3): 345–362. Sun J G. Methods for numerical modeling of geophysical fields under complex topographical conditions: a critical review. Global Geology (in Chinese) , 2007, 26(3): 345-362. |
| [7] | 强建科. 起伏地形三维电阻率正演模拟与反演成像研究. 武汉: 中国地质大学地球物理与信息技术专业, 2006 . Qiang J K. The research on 3-D resistivity forward and inversion algorithm on undulate topography (in Chinese). Wuhan: Geodetection and Information Technology Department of China University of Geosciences, 2006 . |
| [8] | 王雪秋, 孙建国. 地震波有限差分数值模拟框架下的起伏地表处理方法综述. 地球物理学进展 , 2008, 31(1): 40–48. Wang X Q, Sun J G. The state-of-the-art in numerical modeling including surface topography with finite-difference method. Progress in Geophysics (in Chinese) , 2008, 31(1): 40-48. |
| [9] | 罗延钟, 万乐. 二维地形不平条件下外电场的有限差分模拟. 物探化探计算技术 , 1984, 6(4): 15–26. Luo Y Z, Wan L. Finite difference modeling of exterior electrical field under non-planar surface condition. Computational Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1984, 6(4): 15-26. |
| [10] | 吴小平, 徐果明, 李时灿. 利用不完全Cholesky共轭梯度法求解点源三维电场. 地球物理学报 , 1998, 41(6): 848–855. Wu X P, Xu G M, Li S C. The calculation of three-dimensional geoelectric field of point source by incomplete Cholesky conjugate gradient method. Chinese J. Geophys. (in Chinese) , 1998, 41(6): 848-855. |
| [11] | 罗延钟, 张桂青. 电子计算机在电法勘探中的应用. 武汉: 武汉地质学院出版社, 1987 . Luo Y Z, Zhang G Q. Application of Electric Computers in Electrical Exploration (in Chinese). Wuhan: Wuhan College of Geology Press, 1987 . |
| [12] | 徐世浙. 地球物理中的有限单元法. 北京: 科学出版社, 1994 . Xu S Z. The Finite Element Method in Geophysics (in Chinese). Beijing: Science Press, 1994 . |
| [13] | 熊彬, 阮百尧, 罗延钟. 复杂地形条件下直流电阻率异常三维数值模拟研究. 地质与勘探 , 2003, 39(4): 60–64. Xiong B, Ruan B Y, Luo Y Z. 3-D numerical simulation study of DC resistivity anomaly under complicated terrain. Geology and Prospecting (in Chinese) , 2003, 39(4): 60-64. |
| [14] | Sasaki Y. 3-D resistivity inversion using the finite-element method. Geophysics , 1994, 59: 1839-1848. DOI:10.1190/1.1443571 |
| [15] | 强建科, 罗延钟. 三维地形直流电阻率有限元法模拟. 地球物理学报 , 2007, 50(5): 1606–1613. Qiang J K, Luo Y Z. The resistivity FEM numerical modeling on 3-D undulating topography. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1606-1613. |
| [16] | Xu S Z, Gao Z C, Zhao S G. An integral formulation for three-dimensional terrain modeling for resistivity surveys. Geophysics , 1988, 53: 546-552. DOI:10.1190/1.1442486 |
| [17] | 徐世浙, 王庆乙, 王军. 用边界单元法模拟二维地形对大地电磁场的影响. 地球物理学报 , 1992, 35(3): 380–387. Xu S Z, Wang Q Y, Wang J. Modeling 2-D terrain effect on MT by the boundary element method. Chinese J. Geophys. (in Chinese) , 1992, 35(3): 380-387. |
| [18] | 徐世浙. 地球物理中的边界单元法. 北京: 科学出版社, 1995 . Xu S Z. Boundary Element Method in Geophysics (in Chinese). Beijing: Science Press, 1995 . |
| [19] | 黄兰珍, 田宪漠, 寸树苍. 点源场电阻率法二维地形改正边界元法. 物探化探计算技术 , 1986, 8(3): 201–207. Hang L Z, Tian X M, Cun S C. The boundary element method of the 2-D topographic correction for the resistivity method in the point source field. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1986, 8(3): 201-207. |
| [20] | 徐世浙. 电导率分层线性变化的水平层的点电源电场的数值解. 地球物理学报 , 1986, 29(1): 84–90. Xu S Z. A numerical method for solving electric field of point source on a layered model with linear change of conductivity in each layer. Chinese J. Geophys. (in Chinese) , 1986, 29(1): 84-90. |
| [21] | Zhao S, Yedlin M J. Multidomain Chebychev spectral method for 3-D resistivity modeling. Geophysics , 1996, 61(6): 1616-1623. DOI:10.1190/1.1444080 |
| [22] | Beasley C W, Ward S H. Three-dimensional mise-a-la-masse modeling applied to mapping fracture zones. Geophysics , 1986, 51(1): 98-113. DOI:10.1190/1.1442044 |
| [23] | Oppliger G L. Three-dimensional terrain corrections for mise-a-la-masse and magnetometric resistivity surveys. Geophysics , 1984, 49: 1718-1729. DOI:10.1190/1.1441579 |
| [24] | 孙章庆, 孙建国, 张东良. 2.5维起伏地表条件下坐标变换法直流电场数值模拟. 吉林大学学报: 地球科学版 , 2010, 40(2): 425–431. Sun Z Q, Sun J G, Zhang D L. 2.5-D DC electric field numerical modeling including surface topography using coordinate transformation method. Journal of Jilin University: Earth Science Edition (in Chinese) , 2010, 40(2): 425-431. |
| [25] | Erdogan E, Demirci I, Candansayar M E. Incorporating topography into 2D resistivity modeling using finite-element and finite-difference approaches. Geophysics , 2008, 73(3): F135-F142. DOI:10.1190/1.2905835 |
| [26] | Dey A, Morrison H F. Resistivity modeling for arbitrarily shaped two-dimensional structures. Geophysical Prospecting , 1979, 27: 106-136. DOI:10.1111/gpr.1979.27.issue-1 |
| [27] | Mufti I R. Finite-difference resistivity modeling for arbitrarily shaped two-dimensional structures. Geophysics , 1976, 41: 62-78. DOI:10.1190/1.1440608 |
| [28] | 谢胜百. 不可压流场计算中的浸入式边界方法及其改进. 北京: 北京航空航天大学航空宇航推进理论与工程专业, 2009 . Xie S B. The immersed boundary methods and modifications in simulations of unsteady viscous incompressible flows (in Chinese). Beijing: School of Jet Propulsion Beihang University, 2009 . |
| [29] | 宫兆新, 鲁传敬, 黄华雄. 浸入边界法及其应用. 力学季刊 , 2007, 28(3): 353–362. Gong Z X, Lu C J, Hung H X. Immersed Boundary Method and Its Application. Chinese Quarterly of Mechanics (in Chinese) , 2007, 28(3): 353-362. |
| [30] | 谢胜百, 单鹏. 两种侵入式边界方法的比较. 力学学报 , 2009, 41(5): 618–627. Xie S B, Shan P. Comparisons of two types of immersed boundary methods in numerical simulations of a cylinder in uniform incompressible flows. Chinese Journal of Theoretical and Applied Mechanics (in Chinese) , 2009, 41(5): 618-627. |
| [31] | 陆金甫, 关治. 偏微分方程数值解法(第2版). 北京: 清华大学出版社, 2004 . Lu J P, Guan Z. Numerical Solution of Partial Differential Equations (2nd Edition) (in Chinese). Beijing: Tsinghua University Press, 2004 . |
| [32] | 徐世浙. 点电源二维电场问题的付氏变换的波数k的选择. 物探化探计算技术 , 1988, 10(3): 235–239. Xu S Z. Selection of wave number k in Fourier inverse transformation for point source and 2-D electric field problems. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1988, 10(3): 235-239. |
| [33] | Jung J Y, Lee H, Chen M M. Simple, accurate treatment of curved boundaries with dirichlet and neumann conditions. Numerical Heat Transfer, Part B , 2004, 45: 421-448. DOI:10.1080/10407790490277913 |
| [34] | 张东良, 孙建国, 孙章庆. 二维起伏地表直流电场插值法数值模拟. 世界地质 , 2009, 28(2): 242–248. Zhang D L, Sun J G, Sun Z Q. Finite-difference DC electrical field interpolation modeling on two dimension undulate topography. Global Geology (in Chinese) , 2009, 28(2): 242-248. |
| [35] | 孙建国. 直流电场带地形数值模拟. 资源高技术论坛, 长沙, 2008. Sun J G. DC electric field numerical modeling including surface topography (in Chinese). High-tech Forum Resource Changsha, Changsha 2008 |
| [36] | Sun J G, Zhang D L, Sun Z Q. A finite difference method for modeling the DC electrical potential field including surface topography. 79nd Annual International Meeting, SEG, Expanded Abstracts, 2009. 664~668 |
| [37] | 刘国兴. 电法勘探原理与方法. 北京: 地质出版社, 2005 . Liu G X. The principle and method of electrical exploration (in Chinese). Beijing: The Geological Publishing House, 2005 . |
| [38] | 韩江涛. 起伏地表三维电阻率法数值模拟与分析. 长春: 吉林大学地球探测科学与技术学院, 2009 . Han J T. Numerical simulation and analysis of 3D resistivity method on irregular topography (in Chinese). Changchun: College of Geoexploration Science and Technology of Jilin University, 2009 . |
| [39] | 杨华军. 数学物理方法与计算机仿真. 北京: 电子工业出版社, 2005 . Yang H J. Methods of Mathematical Physics and Computer Simulation (in Chinese). Beijing: Electronics Industry Publishing, 2005 . |
 2011, Vol. 54
2011, Vol. 54

