一般在三维情况下,我们很难得到大地电磁场的解析解,因此只有借助解偏微分方程或者积分方程的数值计算方法来求出近似解.目前,大地电磁场三维正演计算方法主要包括积分方程法、有限差分法、有限元法等.其中积分方程法被用于三维大地电磁场正演模拟的频率最高.Wannamaker[1]首先将积分方程方法运用到大地电磁测深的三维模拟中,Mackie等[2]比较了积分方程方法与有限差分方法,指出两种方法除了在导电性分界面和高阻体方面不同,计算精度是一致的.后来Xie等[3]提出了更为复杂的磁场积分方程法.这种方法及其结果后来成为其他方法的参照标准.但是积分方程法对于复杂的地电体,由于所形成的矩阵是满阵,内存开销极大而难以在一般微机上运行.
Pankratov等[4~7]提出了一种精确的、稳定的和宽频的三维电磁场正演计算方法.该方法使用体积积分方程法,利用改进的Neumann序列(MNS)技术来求解Maxwell方程.并且已经成功地应用于各种三维地球电磁场正演模拟中.该方法的精确性表现在它同时考虑了传导、极化和位移电流.该方法和传统的积分方程法相比,因为采用了MNS技术,成功地避免了解大型的线性方程组,这样就为正演模拟复杂地电异常体提供了条件.
目前三维MT正演的一个主要问题是计算效率偏低,本文正是针对这一问题并在前人研究基础上,考虑采用了一套能提高计算效率的组合方法,即引入广义双共轭梯度法[8, 9]求解改进的Neumann序列的解,同时尝试将格林函数变换到波数域进行分解,以减少计算格林函数的个数,从而降低计算量,提高计算效率.最后通过模型计算和比较,证明本文理论的正确性和有效性.
2 积分方程法的基本原理[10]电导率为σ1的半空间中有一异常块体,其电导率为σ(r)是变化的,为r的函数(r表示矢径).根据Maxwell方程、积分方程理论以及相应的电磁张量格林函数,电磁场可以被分成两部分,一部分是一次场,上角标p表示,即为层状介质中的场,可以很容易地求出.另一部分为二次场,用上角标s表示,可以认为是由异常体中的散射电流Jq引起的.二次电场可以通过将散射电流源Jq乘以适当的格林函数G(r,r′)并对异常体所占的体积做积分而得到:
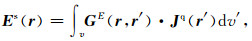
|
(1) |
其中Jq=(σ(r)-σ1)E,v为异常体体积.式中的格林函数是在存在空气-地球界面情况下将r处的二次电场与r′处的电流元Jq(r′)联系起来.
将一次场和二次场相加,于是可以得到实测电场表达式为:
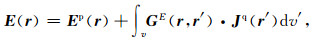
|
(2) |
同时,根据H=∇×E/iωμ,可以得到:
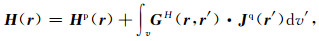
|
(3) |
其中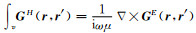
根据MNS技术[4~7],电场和磁场的总场是由一次电流Jp在三维介质中激发的,由于考虑了位移电流,因此在这里定义广义电导率ζ(r,ω)=σ(r,ω)-iωε(r,ω),ε为介电常数.
散射电流Jq则变为
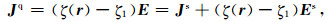
|
(4) |
其中
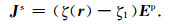
|
(5) |
根据Maxwell方程组可以得到表示未知二次场Es(r)的传统散射公式:
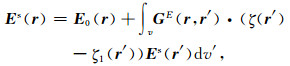
|
(6) |
其中
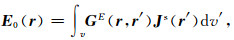
|
(7) |
式(6)的精确解可以被写成无限Neumann序列,而E0(r)即为Es(r)的零阶近似:
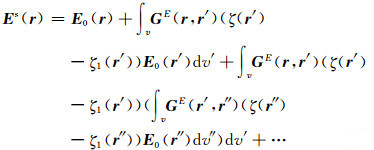
|
(8) |
我们知道上式的收敛性是不能被保证的,特别是当二次电场与E0(r)差别很多的情况下该序列完全不能收敛.但是,如果我们在(6)式的两边同时加上(ζ(r)-ζ1(z))Es/2Re(ζ1(z))(Re(ζ1)表示的ζ1实部),同时将变量改写为:
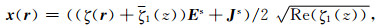
|
(9) |
其中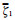
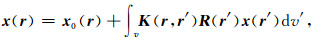
|
(10) |
该方程的解可以被写成Neumann序列的形式,而且该序列被证明为收敛序列[4]:
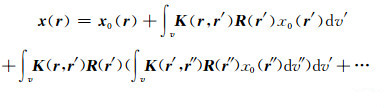
|
(11) |
其中
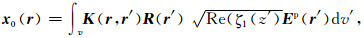
|
(12) |
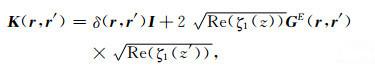
|
(13) |
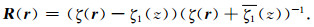
|
(14) |
δ(r)为Dirac函数,I为单位矩阵.
对于式(10),我们可以使用很多迭代的计算方法求解,本文中使用广义双共轭梯度方法(GPBi-CG)[8, 9]来求解.
当得到x(r)的值后,根据式(4)、(5)和(9)即可求出散射电流Jq,并根据式(1)计算得到二次场的电场值Es,于是实测电场强度E=Ep+Es就可以被求得.同时根据式(3)可以计算得出实测磁场强度H的值.
在此,同时给出本方法的计算流程如下:(1)读入模型和剖分参数;(2)计算一维背景的电磁场强度;(3)计算格林函数值;(4)用GPBI-CG迭代计算三维模型的电磁场强度,当达到精度后结束迭代;(5)计算视电阻率与相位值.
3 广义双共轭梯度法(GPBi-CG)广义双共轭梯度法(GPBi-CG)[8, 9]可以看成是一种Krylov子空间方法,文献[9]详细比较了各种Krylov子空间迭代方法对于求解形如Ax=b的线性方程组效率和精度,最后证明广义双共轭梯度法是一种有效的方法.于是尝试使用该方法求解式(10)中的x(r)值.广义双共轭梯度法(GPBi-CG)具体计算流程如下:
x0为初始值,r0=b-Ax0,令r0*=r0,u-1=t-1=w-1=0,β-1=0.
开始迭代,n=0,1,……
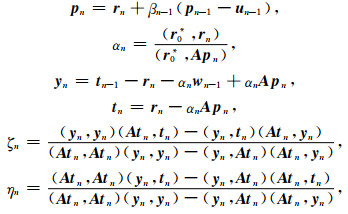
|
(如果n=0,那么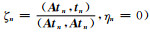
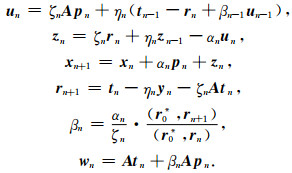
|
当‖r‖≤ε‖b‖(ε为一小值)时,结束迭代.
对于式(10),经过变形可以得到如下的形式:
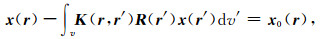
|
(15) |
令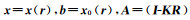
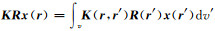
本文在迭代过程中将收敛精度设为l(10-5),通常只需要16次左右的迭代就可以达到收敛精度,而一般的共轭梯度法(CG)需要20次以上的迭代[9],同时迭代过程中误差也是一直减小,说明迭代过程很稳定.因此证明将GPBi-CG应用于对MNS技术中x的迭代求解是合适而且有效的.
4 格林函数的计算方法通常使用快速汉克尔变换直接求解[11, 12]计算格林函数,本文通过将格林函数变换到波数域,并将其分解为两部分,通过toroidal-poloidal分解[13]的原理来求解,此方法将原先方法中需要计算约Nx×Ny×Nz×Nz个单元减少为只需要约8×Nx×Ny×Nz个单元,由于一般情况下Nz是一个相对大的数字,因此这样改变以后就可以大大减少计算单元,从而可以提高计算的效率并且节省内存量.下面就给出其计算原理.
对于式(1),进行傅里叶变换后可得
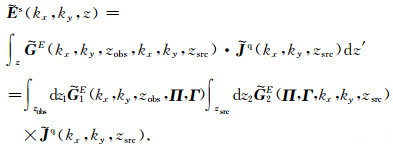
|
(16) |
其中kx,ky为x与y方向上的波数,zobs、zsrc分别表示观测点和源点的深度.
如何获得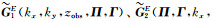
为了证明上述理论的正确和有效性,本文对两个模型进行计算,并与其他方法进行对比.
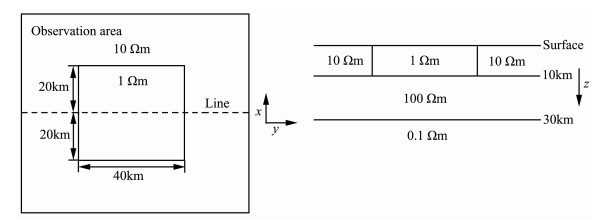
模型一见图 1,剖分参数如下:水平方向x、y的间隔为1km,垂直方向取如下深度值:0、10、20、30、40、50、60、70、80、90、100、110、120、130、140、150、180、220、270、320、390、460、560、670、810、970、1200、1400、1700、2000、2400、2900、3500、4200、5000、6100、7300、8500、10000、30000m.取测线所对应的值,同时与三维交错网格有限差分法[15, 16](RandyMackie编写,取相同的模型剖分)的计算结果进行对比,计算参数如下:本方法的观测区域为80km×80km,而有限差分法,考虑到边界的影响,其观测区域为120km×120km,异常体的中心点与观测区域的中心点重合.图 2是周期为100s时的结果.
|
图 1 模型一 Fig. 1 Model I |
|
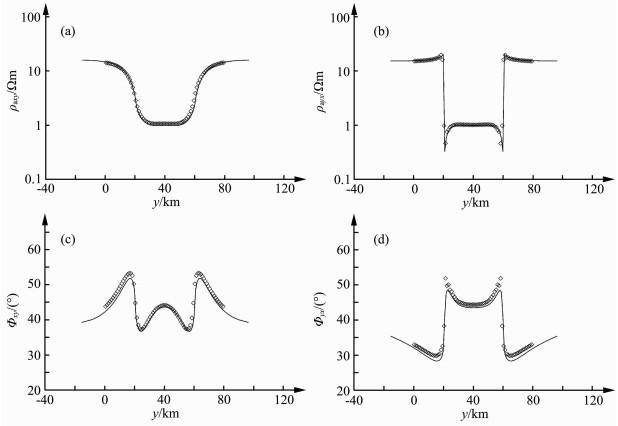
图 2 周期100s正演模拟结果(◇为本文结果, 曲线为三维有限差分法结果) (a)视电阻率ρaxy; (b)视电阻率ρayx; (c)相位Φxy; (d)相位Φyx. Fig. 2 Forward modeling results of 100 s period (◇ is our result, curve is 3D FDM result) (a) Apparent resistivity ρaxy; (b) Apparent resistivity ρayx; (c) Phase Φxy; (d) Phase Φyx. |
可以看到本方法结果基本吻合模型的电性变化,且与有限差分法正演的结果基本一致.
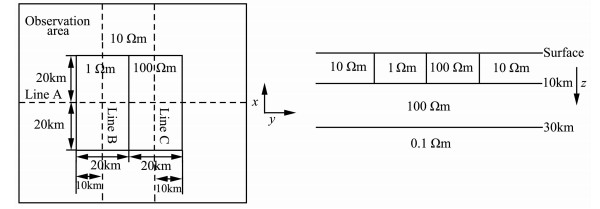
模型二见图 3,对此模型用本方法以及三维交错网格有限差分法进行计算,剖分参数和计算参数与模型一相同.取测线A、B、C上的值(如图 3所示)进行比较,图 4,5,6为模拟结果(其中A、B测线为100s结果,C测线为10s结果).
|
图 3 模型二 Fig. 3 Model Ⅱ |
|
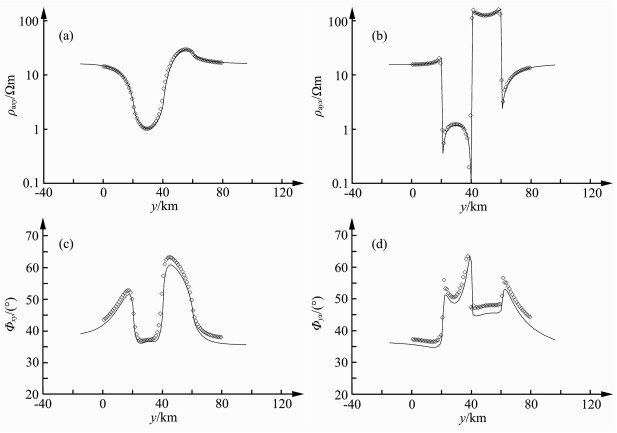
图 4 测试A周期100s正演模拟结果(◇为本文结果, 曲线为三维有限差分法结果) (a)视电阻率ρaxy; (b)视电阻率ρayx; (c)相位Φxy; (d)相位Φyx. Fig. 4 Forward modeling results of 100 s period on line A (◇ is our result, curve is 3D FDM result) (a) Apparent resistivity ρaxy; (b) Apparent resistivity ρayx; (c) Phase Φxy; (d) Phase Φyx. |
|
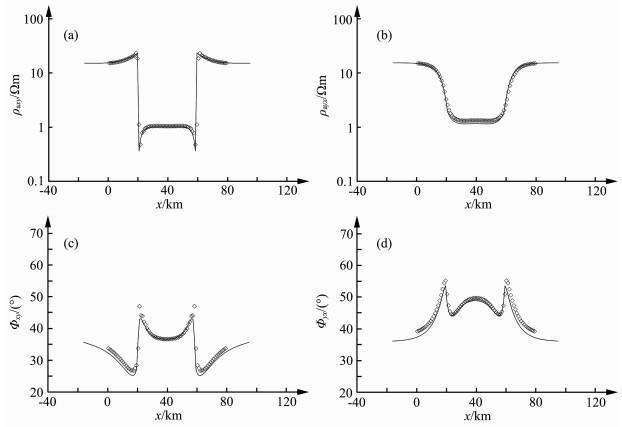
图 5 测试B周期100s正演模拟结果(◇为本文结果, 曲线为三维有限差分法结果) (a)视电阻率ρaxy; (b)视电阻率ρayx; (c)相位Φxy; (d)相位Φyx. Fig. 5 Forward modeling results of 100 s period on line B (◇ is our result, curve is 3D FDM result) (a) Apparent resistivity ρaxy; (b) Apparent resistivity ρayx; (c) Phase Φxy; (d) Phase Φyx. |
|
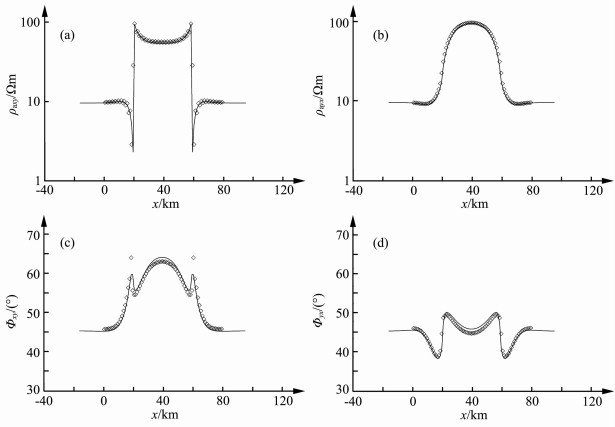
图 6 测试C周期100s正演模拟结果(◇为本文结果, 曲线为三维有限差分法结果) (a)视电阻率ρaxy; (b)视电阻率ρayx; (c)相位Φxy; (d)相位Φyx. Fig. 6 Forward modeling results of 100 s period on line C (◇ is our result, curve is 3D FDM result) (a) Apparent resistivity ρaxy; (b) Apparent resistivity ρayx; (c) Phase Φxy; (d) Phase Φyx. |
从图 4~6中可以看到,曲线的形态与该测线位置对应的模型电性变化相一致.同时,在视电阻率方面,两种方法在测线上的计算结果都比较吻合.而在相位方面,可以看到在高阻体处两者相当吻合,而在低阻体处会有一些差别,估计原因在于有限差分法在地表需要更加精细的纵向剖分,从而导致对上述模型的计算精度不如本文方法精度高.
另外,从计算时间上看,本方法也是占有优势的.对于模型二,在同一配置的服务器上(4GB内存的PANYA服务器)计算1、10、100、1000s四个周期总共需要的时间,本方法为14~16min(取决于MNS迭代精度),而对于交错网格有限差分法,则需要50min以上.
6 结论目前,三维大地电磁正演模拟中的主要问题还是计算效率比较低,本文针对此问题,在已有的MNS技术的基础上,采用在Krylov子空间迭代方法中被证明对解大型线性方程组更有效的广义双共轭梯度法来迭代求解改进的Neumann序列,该方法与其他迭代方法相比稳定性更好,收敛更快.同时利用了toroidal-poloidal分解以及将格林函数分解为两部分的思想求解格林函数,这样与传统的快速汉克尔变换相比就大大减少了计算的单元数,从而提高计算效率并且节省内存量.最后设计了两个模型进行试验,并与交错网格有限差分法三维正演模拟方法对比后,证明该方法的计算结果是稳定和有效且在计算速度上是具有优势的.
以后的工作将继续考虑在不同频率点上使用不同的纵向剖分进行计算以及对于起伏地表情况下的正演模拟,从而使用三维正演速率更快,更加实用化.
附录
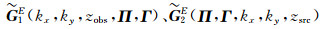
|
求解过程
考虑层状介质中频率域Maxwell方程如下:
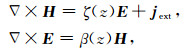
|
(A1) |
其中ζ(z)=σ(z)+iωε(z),β(z)=iωμ(z).
在无源区域,jext=0,E、H无散,应用toroidal-poloidal分解:
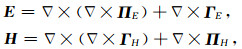
|
(A2) |
其中ΠH(r)=ζΠE(r),ΓE(r)=βΓH(r),且Π(r),Γ(r)只含有z方向的分量Π(r)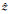
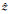
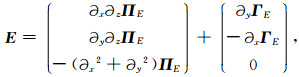
|
(A3) |
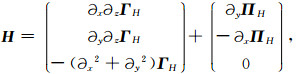
|
(A4) |
且
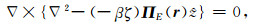
|
(A5) |
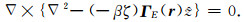
|
(A6) |
进行空间-波数域二维傅里叶变换,得到:
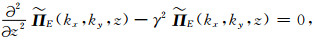
|
(A7) |
其中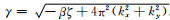
所以,我们就可以得到一般解为:
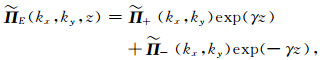
|
(A8) |
特殊情况下,在顶层时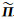
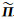
同理可得:
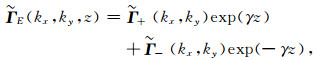
|
(A9) |
在连续的情况下,满足边界条件:
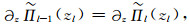
|
(A10) |
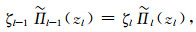
|
(A11) |
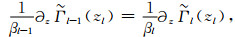
|
(A12) |
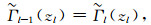
|
(A13) |
这样,我们就可以求得无源情况下每一层内Π(r)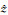
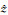
下一步,考虑源项后,我们重新定义电场强度:
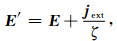
|
(A14) |
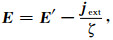
|
(A15) |
于是
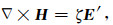
|
(A16) |
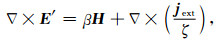
|
(A17) |
当jext=δ(r,r0)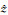
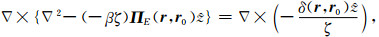
|
(A18) |
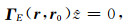
|
(A19) |
进行空间-波数域二维傅里叶变换后可得,
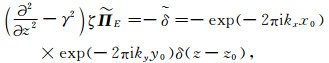
|
(A20) |
求解得
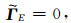
|
(A22) |
当jext=δ(r,r0)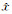
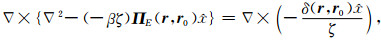
|
(A23) |
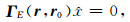
|
(A24) |
于是,
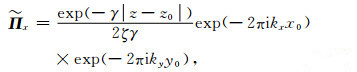
|
(A25) |
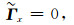
|
(A26) |
由toroidal-poloidal分解,可以得到,
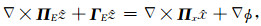
|
(A27) |
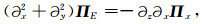
|
(A28) |
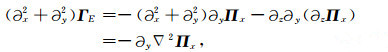
|
(A29) |
进行空间-波数域傅里叶变换后,可得,
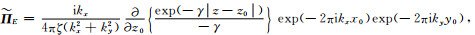
|
(A30) |
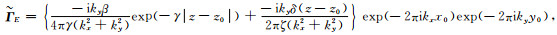
|
(A31) |
同理可得,当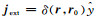
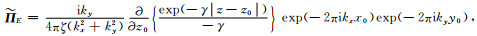
|
(A32) |
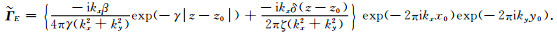
|
(A33) |
根据式(A21)、(A22)、(A30)、(A31)、(A32)、(A33)可求得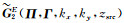
同时,对式(A3)进行空间-波数域二维傅里叶变换得:
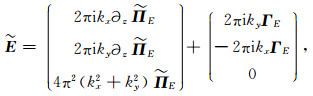
|
(A34) |
由式(A34)则可求得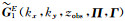
衷心感谢日本东京大学地震研究所的H.Utada教授,K.Baba助教,T.Koyama助教对本算法研究过程中给予的极大帮助.同时,感谢各位评审专家对本文提出的中肯评价和意见,使作者能更好地完善本文.
| [1] | Wannamaker P E, Hohmann G W, SanFilipo W A. Electromagnetic modeling of three dimensional bodies in layered earths using integral equations. Geophysics , 1984, 49(1): 60-74. DOI:10.1190/1.1441562 |
| [2] | Mackie R L, Madden T R, Wannamaker P E. Three dimensional magnetotelluric modeling using difference equations-Theory and comparisons to integral equation solutions. Geophysics , 1993, 58(2): 215-226. DOI:10.1190/1.1443407 |
| [3] | Xie G Q, Li J H, Majer E L, et al. 3-D electromagnetic modelling and nonlinear inversion. Geophysics , 2000, 65(3): 804-822. DOI:10.1190/1.1444779 |
| [4] | Pankratov O V, Kuvshinov A V, Avdeev D B. High performance three-dimensional electromagnetic modeling using a modified Neumann series:Anisotropic case. J. Geomag. Geoelectr. , 1997, 49: 1541-1547. DOI:10.5636/jgg.49.1541 |
| [5] | Avdeev D B, Kuvshinov A V, Pankratov O V, et al. High-performance three-dimensional electromagnetic modeling using a modified Neumann series. Wide-band numerical solution and example. J. Geomag. Geoelectr. , 1997, 49: 1519-1539. |
| [6] | Avdeev D B, Kuvshinov A V, Pankratov O V, et al. Three-dimensional induction logging problems, Part I:An integral equation solution and model comparisons. Geophysics , 2002, 67(2): 413-426. DOI:10.1190/1.1468601 |
| [7] | Pankratov O V, Avdeev D B, Kuvshinov A V. Electromagnetic field scattering in a heterogeneous earth:A solution to the forward problem. Physics Solid Earth , 1995, 31: 201-209. |
| [8] | Zhang S L. GPBi-CG:Generalized Product-type Methods Based on Bi-CG for Solving Nonsymmetric Linear Systems. SIAM Journal on Scientific Computing , 1997, 18(2): 537-551. DOI:10.1137/S1064827592236313 |
| [9] | Zhang S L. A class of product-type Krylov-subspace methods for solving nonsymmetric linear systems. Journal of Computational and Applied Mathematics , 2002, 149: 297-305. DOI:10.1016/S0377-0427(02)00537-X |
| [10] | Zhdanov M S, Wannamaker P E. Three-dimension electromagnetics. Methods in Geochemistry and Geophysics, Elsevier , 2002, 35: 21-42. DOI:10.1016/S0076-6895(02)80084-1 |
| [11] | 张辉, 李桐林, 董瑞霞, 等. 利用高斯求积和连分式展开计算电磁张量格林函数积分. 地球物理学进展 , 2005, 20(3): 667–670. Zhang H, Li T L, Dong R X, et al. Computation of Green's tensor integrals for electromagnetic problems using Gaussian quadrature and continued fraction. Progress in Geophysics (in Chinese) , 2005, 20(3): 667-670. |
| [12] | 徐凯军, 李桐林, 张辉, 等. 利用积分方程法的大地电磁三维正演. 西北地震学报 , 2006, 28(2): 104–107. Xu K J, Li T L, Zhang H, et al. Three dimensional magnetotelluric forward modeling using integral equation. Northwestern Seismological Journal (in Chinese) , 2006, 28(2): 104-107. |
| [13] | Backus G. Poloidal and Toroidal Fields in Geomagnetic Field Modeling. Rev. Geophys. , 1986, 24(1): 75-109. DOI:10.1029/RG024i001p00075 |
| [14] | Weaver J T. Mathematical Methods for Geo-electromagnetic Induction. Research Studies Press, Wiley, 1994 http://citeseerx.ist.psu.edu/showciting?cid=1486477 |
| [15] | Mackie R L, Madden T R. Conjugate gradient relaxation solutions for three dimensional magnetotelluric modeling. Geophysics , 1993, 58(7): 1052-1057. DOI:10.1190/1.1443481 |
| [16] | Mackie R L, Smith J T, Madden T R. Three-dimensional electromagnetic modelling using finite difference equations:the magnetotelluric example. Radio Sci , 1994, 29: 923-935. DOI:10.1029/94RS00326 |
 2010, Vol. 53
2010, Vol. 53


