2. 中国科学院测量与地球物理研究所动力测量重点实验室, 武汉 430077
2. CAS Key Laboratory of Dynamic Geodesy, Institute of Geodesy and Geophysics, Academy of Sciences, Wuhan 430077, China
地震震源深度一直是地球科学家关注的问题.首先,震源深度是地震危险性和强地面震动研究的重要参数,一般说来浅源地震可以造成相对严重的损失.例如1993年的印度Latur地震,由于震源深度只有2km,一个6级地震就造成了近万人的死亡[1].同时,震源深度的研究,对于地震孕育和发生的深部环境,地震能量集结、释放的活动构造背景,以及地壳内部构造变形及其动力学属性等都有非常重要的意义[2].具体地说,震源深度是反映地壳脆性-韧性转化深度的重要参数,对于确定地壳的流变结构具有关键的意义[3].
但是如何精确确定震源深度一直是个难题.通常的用Pg (Sg)走时定位只有在台网密集、震中距较小的情况下才能获得较高精度的震源深度.而在台网相对稀疏的情况下问题尤显突出,由于缺少近台资料,同时较远处台站的地震波走时对深度不够敏感,使得精确确定深度很困难.所幸的是,我们可以利用深度震相来提高深度精度,中强震(≥M5)的远震波形有较高信噪比,通常可以使用远震深度震相sP或pP来确定震源深度,但是对于更小的地震则要求助于近震深度震相.
对于地壳结构相对简单的区域,近震深度震相sPg,sPmP和sPn,以及它们的参考震相Pg,PmP和Pn在近震记录上通常可以清楚地观测到[4~18].在近震地震图上识别出这些深度震相及其参考震相后,可以利用测量它们之间的到时差或通过波形对比的方法相对精确的确定震源深度,在这方面国内外学者作了不少研究.
Langston[7]利用sPg (其文章中称之为sP)和Pg的相对到时差研究了1968年澳大利亚Meckering近震序列的深度分布.Bock等[12]利用sPmP测量了近震震源的深度.Saikia等[15]利用波形拟合的方法通过拟合sPmP,pPmP以及PmP震相进一步标定震源的深度.Kim等[19]和Kastrup等[20]利用了sPmP和PmP的到时与理论波形的对比确定了部分近震的深度.Saikia[14]在实际数据和理论波形中都发现对确定的震源深度sPn相对Pn的到时差很稳定的特征,因此可以用来约束震源深度.Ma和Atkinson[18]对sPg,sPmP,sPn等深度震相做了较详细的研究,利用sPmP和PmP的特征研究了近震震源深度,就这些深度震相对速度结构模型、机制解、水平位置的敏感性做了探讨.Langston[8]还对上地幔地震的深度震相SsPmp做了研究,利用来自Moho以下的地震波形上较显著的震相SsPmp和Sp,通过到时以及波形研究确定了地震的深度,并指出该震相在研究深震和中深度地震时的重要性.
在国内主要开展了一些用sPn震相计算震源深度的研究.房明山等[21]采用sPn-Pn走时差方程计算了山西、华北、甘肃、青海、华东和四川地区的sPn-Pn走时表,建立了sPn-Pn走时差求震源深度曲线图,并应用于震例检验.任克新等[22]应用相同的方法用sPn计算了2003年8月16日内蒙古6级地震的震源深度.洪星等[23]用此方法计算了台湾海峡南部一次5.0级地震的震源深度.高立新等[24]使用双层地壳模型,建立sPn与Pn波的走时差方程,最终导出区域性震深深度与sPn与Pn走时差之间的线性关系,通过测量这两个震相的走时差来确定震源深度.
国内外的研究表明,利用这些深度震相的特征可以有效地提高震源深度精度.但是也必须注意到,不同的深度震相一般有其优势的震中范围和使用条件,科学地利用它们才能获得相对合理的结果.对于地壳厚度30多公里,结构相对简单的地区,近震深度震相的可观测震中范围通常具有如下特征:sPg是S波经过地表反射转换为P波的震相,通常在60~100km范围内可以清楚地观测到; sPmP由于其较强的振幅,通常可以传播较远的距离,一般在180~350km左右发育较好; 而sPn相对于sPg和sPmP来说是一个较弱的震相,一般出现在300km左右,通常只有中强震可以产生较强的sPn[18].值得注意的是,这些震相一般要在较远的震中距离上才能观测到,因此对于震级相对较大的地震才能应用.而50km以内的地震波形通常具有较高的信噪比,但是一直没有被用来约束中小地震的深度,如果我们能充分利用较近距离(50km以内) P和S之间的波形信息,则可以获得更多中小地震的深度信息.
在文中,我们将提出一个新的震相sPL,研究它的特征,并探讨它在确定震源深度方面的应用.
2 sPL震相对于较近地震,sPg是一个很好的深度震相,Langston[7, 25]的研究表明sPg-P的到时差受模型不确定性影响很小,因此利用sPg可以精确确定震源深度,即使所给的震中距不是很精确也可以获得精确的深度结果.可是sPg只有在上地壳有较大且光滑的速度梯度时才能发育得比较好,而在一般情况下不一定能够形成.
在近距离上会产生另外一个很少有人关注的震相.从震源出发的SV波入射到自由表面下方时将有一部分能量转换为P波,当临界入射时转换P波将沿着地表传播(图 1),Aki称此波为“Surface P-wave”,它的水平视速度和P波速度相等,出现在临界距离上,虽然随距离的变化衰减很快,但是它的起始可能比直达S波尖锐,某些方面具有与首波类似的性质[26].地表P波只定义了上述沿着地表的那一支震相,但是实际情况中,均匀半空间模型太过简单,对于更接近真实的速度随深度增加的模型,可能已经不是一支震相,而包含了临界距离附近P波在浅层(如盖层)的一系列多次反射或转换震相,这些震相与“Surface P-wave”到时较一致而混合在一起.由于该震相是由S和P波相互耦合而产生,同时为了更具普遍意义,我们将Aki定义的“SurfaceP-wave”和这些多次反射折射震相形成的一个波列定义为sPL (s coupled into P wave).其中s表示地震激发的S波部分往上传播.定量地震学已经定义了SPL震相,其对应于远震的S波(从震源向下传播)在Moho下方耦合形成的长周期的P波波列[26],而本文的sPL则是在近距离上只在地表附近传播的波.

|
图 1 均匀半空间下sPL和直达P波射线路径图 Fig. 1 Ray paths of sPL and P wave for the model of half space |
值得注意的是,sPL不同于sPg,它们具有如下的差别:(1)产生机制不同.sPL是S波向上传播在临界距离附近转换为P波并且沿着地表传播的波,在半空间情况下简化为地表P波(surface P wave),而由于自由表面下的速度梯度等结构的存在,sPL可能包含P波在浅部的部分多次波或散射成分.而sPg则是S波经地表反射转换成P波向下传播受速度梯度的影响而回转至地表的震相.(2)两者的可观测震中距离不同.sPL一般出现在较近的震中距离上,在30~50km附近比较容易观测到.而sPg则出现在较远的震中距离上,并且一般在地壳浅部有较光滑正梯度的情况下才能发育得较好.(3)波形特征有较大差别.sPL振幅的径向分量要比垂向分量强,而切向分量的振幅则很弱,同时由于其类似于首波的性质,所含高频成分相对较少,波形一般没有P波尖锐.而sPg震相更类似于Pg,由于其入射角较小,能量则主要集中在竖直分量上,径向分量振幅要比竖直分量小得多,含有较多的高频成分.在观测实际地震波形时注意两者的特征,则不易导致误认震相.
基于上述定义,下面我们将针对均匀半空间,具有沉积层的两层简化模型和半空间梯度模型,用频率-波数(FK)方法[27~29]计算理论地震图来考察sPL震相的特征.
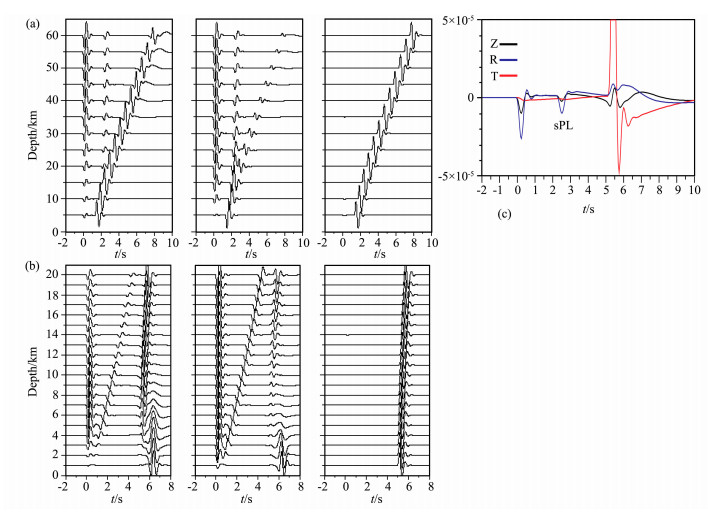
2.1 均匀半空间均匀半空间情况下,由于没有多次波,sPL退化为“Surface P-wave”.此时该震相由两段射线组成,一段由震源向上到地表的S波,另一段是沿着地表传播到台站的P波,图 1为射线路径示意图.我们建立Vp=5.8km/s,Vp/Vs=1.73,Rhou=0.32Vp+ 0.77的半空间模型.由于我们关心的是近距离50km以内直达P波和直达S波以及它们之间的sPL震相,这些震相主要受震源上方的速度结构影响,因此我们用上地壳的平均速度建立半空间模型具有一定的实际意义.如图 2a是用FK方法计算获得的震源深度为10km、机制为走滑型双力偶源的三分量格林函数,采用了0.05~2 Hz的带通滤波.我们看到P波之后,S波之前有一清晰的震相,且在同一地震深度下它与P波之间的到时差随震中距几乎不变,这个震相就是sPL.而在同一震中距离上,sPL相对直达P波的到时随着震源深度的增加几乎呈线性增加(图 2b).这说明,sPL同直达P波之间的到时差可以用来确定震源深度.需要注意的是,sPL并不是在所有近距离震中距上都会出现的,根据临界入射的条件,在一定的速度模型下每个震源深度都有相应的临界距离,只有在这个临界距离之后才可能观测到sPL.同时,我们也注意到由于在均匀半空间情况下sPL简化为地表P波,它的偏振方向主要沿着径向方向,因此径向分量相对垂向分量具有较大的振幅,而切向分量振幅为零,这在图 2c中得以体现.
|
图 2 均匀半空间下,走滑型双力偶源的三分量格林函数波形图,采用了0.05~2 Hz的带通滤波 (a)震源深度10km时速度波形随震中距离的变化图.从左至右依次为竖直、径向和切向分量; (b)震中距为40km速度波形随着震源深度的变化图.从左至右依次为竖直、径向和切向分量; (c)震源深度10km,震中距40km处三分量位移波形的比较图.其中黑色为竖直分量,蓝色为径向分量,红色为切向分量. Fig. 2 Three components Green's functions of a strike-slip double couple source with the half space model, all waveforms are band-passed with frequency range of 0.05~2 Hz (a) Record sections of synthetic ground velocity waveform for the focal depth of 10 km. From left toright:vertical, radial and tangential component; (b) Waveform variation with focal depth at the distance of 40 km. Vertical, radial and tangential components are shown from left to right; (c) Three components displacement waveform at the distance of 40 km with the focal depth of 10 km. |
总的来说,在半空间下sPL相对简单,退化为单一的地表P波,震相清晰,以低频为主,能量主要集中在径向分量,容易识别,并且它与直达P波的到时差随震源深度几乎线性增加,而受震中距离的影响不大,可以用来确定震源深度.
2.2 两层模型对于中生代盆地地区,可以用简化的两层模型模拟波形,进而看沉积层模型下sPL震相的特征.我们选择参数Vp1=4.8km/s,H1=1km,Vp2=5.8km/s,Vp/Vs=1.73建立模型,密度采用Magistrale等[30]的Vp,Vs和密度关系推算.用FK计算该情形下的全波场理论地震图查看sPL的震相特征.值得注意的是,这个模型只适用于具有较坚实沉积盖层的中生代盆地,而对于诸如首都圈这样低速松散的新生代第四纪盆地地区,P波和S波速度低得多,上述的简单两层模型则不适用[31].
通过FK计算获得的理论地震图如图 3所示,分别给出了sPL随着震中距和震源深度的变化.由图 3a的波形发现两层模型下的sPL震相相对均匀半空间情形下要稍微复杂一些,sPL由原本单一震相地表P波转变为一系列震相的组合,这些可能包含地表P波以及在浅层的一系列反射折射震相的组合使得sPL震相变宽.但是,虽然多了一个沉积层,sPL相对直达P波的到时差随着震中距仍然几乎不变.图 3b给出了震中距为40km时波形随着震源深度的变化,可见此时sPL仍然对深度具有很好的敏感性,sPL相对P的到时差仍随着震源深度几乎线性增加.同时,由图 3c的三分量波形比较发现该模型下sPL能量仍主要集中在径向分量.

|
图 3 两层模型下,走滑型双力偶源的三分量格林函数波形图,采用了0.05~2 Hz的带通滤波 (a)震源深度10km时速度波形随震中距离的变化图.从左至右依次为竖直、径向和切向分量; (b)震中距为40km速度波形随着震源深度的变化图.从左至右依次为竖直、径向和切向分量; (c)震源深度10km,震中距40km处三分量位移波形的比较图.其中黑色为竖直分量,蓝色为径向分量,红色为切向分量. Fig. 3 Three components Green′s functions of a strike-slip double couple source with the model of two layered model, all waveforms are band-passed with frequency range of 0.05~2 Hz (a) Record sections of synthetic ground velocity waveform for the focal depth of 10 km. From left to right are vertical, radial and tangential component; (b) Waveform variation with focal depth at the distance of 40 km. Vertical, radial and tangential components are shown from left to right; (c) Three components displacement waveform at the distance of 40 km with the focal depth of 10 km. |
通过以上FK计算理论地震图分析结果,我们发现简化的沉积层模型会使得sPL变得相对复杂,由单一的地表P波转变为一系列震相的组合,震相变宽,但是能量仍然主要集中在径向分量,同时相对直达P的到时差的特征并未显著改变,因此仍然可以用来约束震源深度.
(3)半空间梯度模型
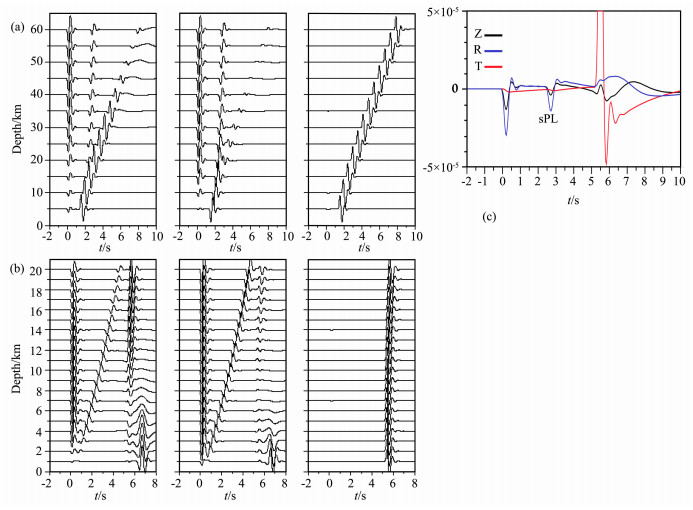
实际的地壳速度可能存在一定的梯度,比较常见情形是越浅处的速度梯度越大[32],因此我们有必要研究在梯度模型下sPL的特征.为了简化问题,突出主要因素,我们研究半空间梯度模型下sPL震相波形,进而观测上地壳梯度结构对sPL的影响.建立Vp_top=5.5km/s,Vp_bottom=6.8 km/s,Vp/Vs=1.73,H=35km,其下为吸收边界的模型,使用FK计算理论地震图.通过图 4,我们可以看出在比较光滑的梯度模型下,sPL震相仍旧清晰,波形相对简单,sPL与直达P波之间的到时差随震中距几乎不变(见图 4a),但是随着震源深度的增加几乎呈线性增加(见图 4b).由图 4c,sPL的能量依旧主要集中在径向分量,竖直分量振幅相对较小.
|
图 4 半空间梯度模型下,走滑型双力偶源的三分量格林函数波形图,采用了0.05~2 Hz的带通滤波 (a)震源深度10km时速度波形随震中距离的变化图.从左至右依次为竖直、径向和切向分量.(b)震中距为40km速度波形随着不同震源深度的变化图.从左至右依次为竖直、径向和切向分量.(c)震源深度10km,震中距40km处三分量位移波形的比较图.其中黑色为竖直分量,蓝色为径向分量,红色为切向分量. Fig. 4 Three components Green's functions of a strike-slip double couple source with the model of gradient velocity model, all waveforms are band-passed with frequency range of 0.05~2 Hz. (a) Record sections of synthetic ground velocity waveform for the focal depth of 10 km. From left to right are vertical, radial and tangential component.(b) Waveform variation with focal depth at the distance of 40 km.Vertical, radial and tangential components are shown from left to right.(c) Three components displacement waveform at the distance of 40 km with the focal depth of 10 km. |
通过观测FK计算的以上三种模型的理论地震图发现,sPL在以上三种模型下都发育得比较好.在均匀半空间情况下相对比较简单,退化为地表P波,简化的沉积层模型下震相相对复杂,但是整体特征不变,在半空间梯度模型下sPL仍可清晰的观测到.sPL的特征具体体现在:形成机理上表现为在自由地表这样大的速度界面上的衍射波,类似于首波,包含部分S波在临界距离附近入射至地表浅层后P波的多次波或散射成分; 没有P波尖锐,高频成分较少,能量主要集中在径向分量,在竖直分量上振幅相对较小,切向分量振幅为零; 出现在临界距离之后,通常在直达P波和直达S波之间可能观测到; 与直达P波之间的到时差随着震源深度的增加几乎呈线性增加,但是对震中距离不敏感,因此可以用来约束震源深度.
3 sPL确定震源深度的实例为了查看sPL用来确定震源深度的可行性,我们将以九江地震为例,仅利用一个台站(九江台)的波形记录上的sPL震相确定九江地震主震和部分余震的深度,并将获得的震源深度同其他方法的结果作对比.
2005年11月26日08时50分,江西省九江-瑞昌交界处发生了ML6.0的地震,造成了较大的人员伤亡和巨大的财产损失[33].震后关于地震主震和余震的空间分布为地震学者和社会所关心.由于台网相对稀疏,离主震较近的只有距离约26km的九江台(JUJ).在主震发生后流动台尚未布置到位时很难精确确定主震和部分余震的深度.因此在稀疏台网布局下,如何利用波形信息精确的确定地震深度显得尤为重要.我们观察研究了九江地震主震及其部分余震在九江台上的波形,通过波形对比法,利用sPL震相获得了主震及部分余震的深度.
通过分析九江地震主震以及部分余震在九江台(JUJ)上的波形记录,我们发现sPL震相特征显著,非常清晰.我们将三分量波形记录旋转至径向、切向和垂向三个分量,在旋转的时候通过使切向分量的P波能量最弱来寻找最佳的旋转角,这样可以避免水平位置定位误差导致不能获得较好的径向和切向分量.然后对数据采用1 Hz以下的低通滤波,并积分至地表位移.主震为200511260850号事件,震级为ML6.0,距九江台26.12km; 200511260925号余震的震级和震中距离分别为ML4.5和28.3km; 200511261256号余震的震级为ML5.3,震中距离为27.42km; 200512030746号余震的震级和震中距离分别为ML4.0和25.92km.图 5为主震和三个余震处理后的三分量位移图.在图中我们可以清晰的观测到sPL震相,并且与理论地震图上预测的特征具有很好的一致性:出现在直达P波之后,S波之前; 径向分量振幅比竖直分量振幅要强,切向分量振幅很弱; 波形呈现低频特征.

|
图 5 九江地震主震(a)和三个余震(b~d)在九江台(JUJ)上的位移波形图 垂向(黑色)、径向(蓝色)和切向(红色). Fig. 5 Waveforms of main event and three aftershocks of Jiujiang earthquake recorded at JUJ station Black line for vertical component, blue and red lines for radial and tangential components respectively. |
观测到如此清晰的sPL震相,为进一步确定震源深度提供了条件.我们采用频率-波数法FK计算理论地震图,利用P和sPL相对到时差可以约束震源深度的特征,对比理论和实际波形并确定震源深度.为了便于同其他研究结果作对比,我们采用了曾被用来反演震源机制的地壳模型[33]计算理论地震图,见表 1.计算每个地震相应震中距上不同震源深度对应的理论地震图,然后将实际波形与这些深度上的理论波形上的直达P和sPL震相的相对到时进行对比,进而获得震源深度.
|
|
表 1 九江地区的速度模型 Table 1 Crustal model of Jiujiang region |
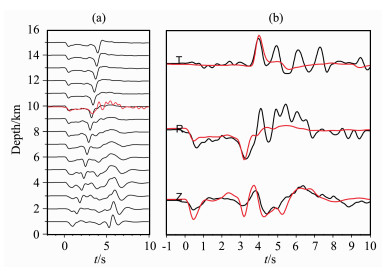
图 6给出了用波形对比法确定主震深度的测试结果,以及最佳震源深度对应的理论波形和实际波形径向分量对比图.在计算理论地震图时,采用了CAP方法反演获得的震源机制[33],并对位移波形采用了1Hz以下低通滤波.图 6a可以看出实际数据(红色)的sPL震相相对直达P的到时与震源深度为10km的理论波形(黑色)对应得很好.同时,我们将实际数据三分量波形(黑色)同震源深度为10km的理论波形(红色)进行比较,证实了结果的可靠性,见图 6b,可见用波形对比法确定主震的最佳深度为10km.震源机制、震中距离的误差S波波形未能得到很好的拟合,但是这并不影响我们深度定位的结果,因为根据sPL的特征,只需要径向分量上直达P和sPL的相对到时吻合得比较好即可.利用同样的方法,我们对三个余震做了处理,通过sPL的波形对比确定了各个地震的深度,结果表明三个余震200511260925,200511261256和200512030746的深度依次为9km,9km和11km,波形对比结果详见图 7~9.
|
图 6 波形对比法确定200511260850主震震源深度 (a)震源深度测试结果图,最佳的震源深度为10km,其中黑色为理论波形,红色为实际数据,均为径向分量; (b)震源深度为10km时的理论位移波形(红色)和实际位移波形(黑色)对比图. Fig. 6 Focal depth determination for 200511260850 main event with waveform comparison method (a) Focal depth sensitivity test with radial component waveforms, the best focal depth is 10 km, black for synthetic waveforms and gray for data; (b) Waveform comparison between data (black) and synthetic waveforms (gray) with best focal depth of 10 km. |
|
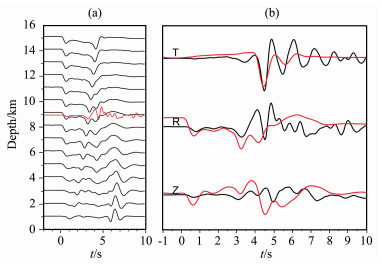
图 7 波形对比法确定余震200511260925的震源深度 (a)震源深度测试结果图.最佳的震源深度为9km,其中黑色为理论波形,红色为实际数据,均为径向分量; (b)震源深度为9km时的理论位移波形(红色)和实际位移波形(黑色)对比图. Fig. 7 Focal depth determination for aftershock 200511260925 with waveform comparison method (a) Focal depth sensitivity test with radial component waveforms, the best focal depth is 9 km; (b) Waveform comparison between data and synthetic waveforms with best focal depth of 9 km. |
|
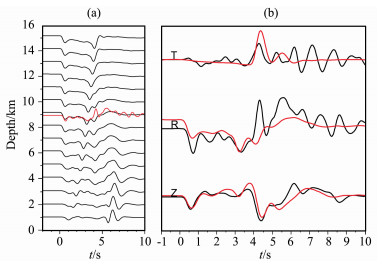
图 8 波形对比法确定余震200511261256的震源深度 (a)震源深度测试结果图.最佳的震源深度为9km,其中黑色为理论波形,红色为实际数据,均为径向分量; (b)震源深度为9km时的理论位移波形(红色)和实际位移波形(黑色)对比图. Fig. 8 Focal depth determination for aftershock 200511261256 with waveform comparison method (a) Focal depthsensitivity test with radial component waveforms, the best focal depth is 9 km; (b) Waveform comparison between data and synthetic waveforms with best focal depth of 9 km. |
|
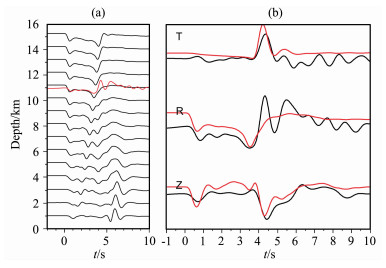
图 9 波形对比法确定余震200512030746的震源深度 (a)震源深度测试结果图.最佳的震源深度为11km,其中黑色为理论波形,红色为实际数据,均为径向分量; (b)震源深度为9km时的理论位移波形(红色)和实际位移波形(黑色)对比图. Fig. 9 Focal depth determination for aftershock 200512030746 with waveform comparison method. (a) Focal depth sensitivity test with radial component waveforms, the best focal depth is 11 km; (b) Waveform comparison between data and synthetic waveforms with best focal depth of 11 km. |
上述利用九江台上观测到的九江地震主震和三个余震的位移波形,由sPL震相的特征,通过波形对比,我们确定了这四个地震的震源深度.将本文方法获得的结果和其他方法获得的深度结果对比,发现采用sPL震相获得的震源深度与其他方法的结果具有很好的一致性.其中本文主震深度为10km,与江西台网定位的9km以及双差定位的11.9km[34],以及CAP波形反演的深度11km[33]都具有很好的一致性.余震200511260925的深度,江西台网定位的结果为9km,双差定位为12.7km[34],CAP波形反演的深度为13km[33],本文的结果为9km.本文对余震200511261256的深度定位结果为9km,江西台网定位的结果为9km,双差定位为12.3km[34].余震200512030746用深度震相sPL波形对比的深度结果为11km,江西台网定位的结果为4km,双差定位为8km[34].
总的来说,本文深度定位结果同其他方法的结果除余震200512030746的结果相差较大外,其他都具有很好的一致性,这表明用sPL震相确定震源深度的可行性.而余震200512030746的深度结果相差较大可能是因为台网相对稀疏[34],只利用走时定位的结果误差可能比较大.
4 讨论本文提出了sPL震相的定义,研究了sPL震相理论波形的特征,并针对2005年九江地震作为实例证实了用sPL震相确定震源深度的可行性.我们注意到,Bouchon[35]曾经对地表P波作了比较详细的研究,但针对的是大地震中地表P波(文中为SP)对强地面震动的影响,他指出实际中该震相几乎没有观测到可能是因为很多被误认为是S波.但是我们关心的是中小地震的sPL震相,在实际观测中相对容易观测到:由sPL以低频为主,能量主要集中在径向分量,垂向分量较小,切向分量振幅很弱,而直达S波的起始一般比较尖锐等特征,sPL不太容易被误认为S波的初至,实际数据的观测也表明sPL是可以观测到的.
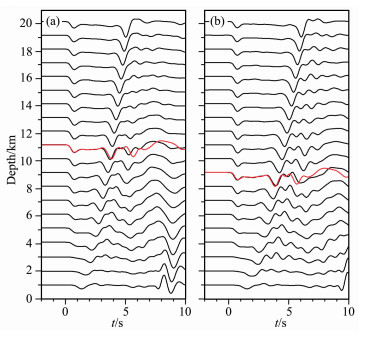
一般地壳模型相对实际模型存在一定的差异,模型参数的误差对用sPL确定的深度有何影响,值得注意.为此,针对九江地震的地壳模型做了利用sPL震相定位震源深度的误差分析.用九江地区标准模型计算机制为主震机制、震源深度10km,在震中距离为40km处的理论波形.然后在九江地区地壳模型基础上产生速度增减10%的两个模型,分别用这两个模型计算地震图通过上述sPL震相波形对比法来确定标准模型下理论地震的深度.通过这样的测试来查看模型不确定性带来的震源深度误差,两个扰动模型对应的定位结果见图 10,其中灰色为机制解与主震机制相同、深度为10km的径向理论波形,黑色为扰动模型不同震源深度的理论波形,均为经过1 Hz以下低通滤波的径向分量位移图.图 10表明速度增减10%的时候,对于深度为10km的地震深度定位分别为11km和9km,也即震源深度的误差约1km,约真实深度的10%,对于20km深的地震误差相应变大.但是已有的研究表明,大陆地壳内的地震深度绝大部分小于20km[2, 36]因此也证明了该方法的可靠性.
|
图 10 模型速度不确定性引起的震源深度误差 (a)速度增加10%时波形对比结果图,深度定位为11km; (b)速度减小10%时波形对比结果图,深度定位结果为9km. Fig. 10 a synthetic test on focal depth error due to uncertainty of velocity model (a) radial waveform comparison with the model increased 10% in velocity; (b) Radial waveform comparison with the model reduced 10% in velocity. |
由sPL产生的机制,以及理论波形研究结果,应该使用震中距大于临界距离的台站上的波形来约束震源深度.而临界距离随着震源深度的增加而增加,由理论波形和实际数据处理我们认为最好采用震中距离在2倍震源深度以外的台站记录的波形,因为在临界距离附近sPL与S波到时相差不大,这将给深度定位带来较大误差.
5 总结本文研究了近距离30~50km附近,通常在直达P之后和S波之前可能观测到的一个震相,根据其产生机制将其定义为sPL震相.研究了sPL的特征以及在确定震源深度方面的应用.
研究表明,sPL震相出现在S波入射到地表的临界距离之后,一般在30~50km附近发育得较好,通常在直达P波之后,S波之前可能观测到,其能量主要集中在径向分量,垂向分量的振幅相对径向要小,切向分量上的振幅很弱,波形高频成分较少,没有P波尖锐.在均匀半空间模型下sPL退化为地表P波,在较复杂的模型下则为地表P波和S波在临界距离附近入射到浅层后转换成P波的一系列多次震相或散射波的组合.
理论波形的计算表明,sPL相对直达P波的到时差对震中距离不敏感,而随着震源深度的增加几乎呈线性增加,利用此特征可以很好地约束震源深度.对2005年九江地震主震和三个余震的深度定位结果证实了用sPL确定震源深度的可行性,正演的误差分析表明10%的速度误差引起小于2km的深度误差,完全在可以接受的范围之内,表明该方法的可靠性.本文通过波形对比法用sPL震相来确定震源深度,也可以采用读取sPL相对直达P波的到时差,将理论和测量的到时差进行对比来确定震源深度.
在观测到sPL震相的情况下,离震源50km以内的一个三分量地震台站的波形就可以帮助获得可靠的震源深度,而不需要精确的震中距离.由于sPL震相出现距离较近,对于较小(三级以上)的地震也可以应用,因此在稀疏台网布局情形下sPL对于确定中小地震深度应该具有很好的应用意义.尤其对于目前我国大部分地区台网都相对稀疏的情况下,充分利用波形特征可以有效的帮助我们提高深度定位的精度.但是需要注意的是,利用sPL震相确定震源深度也是有一定局限性的.首先,这个方法要求有三分量的宽频带地震记录.其次只有在结构相对简单、一维地壳模型能够较好描述的研究区域,sPL才比较容易辨认.而对于结构复杂(如第四纪盆地)或地表大幅度起伏的地区,能否观测到sPL,具有哪些特征,以及是否可以用来确定震源深度等问题还需要进一步研究.
致谢两位匿名评审专家对本文提了宝贵的意见和建议,在此表示衷心的感谢.感谢Dr.LupeiZhu提供F-K计算理论地震图程序.本文中图件由GMT绘图软件完成.
| [1] | Gupta H K, Sarma S V S, Harinarayana T, et al. Fluids below the hypocentral region of Latur earthquake, India:Geophysical indicators. Geophysical Research Letters , 1996, 23(13): 1569-1572. DOI:10.1029/96GL01032 |
| [2] | 张国民, 汪素云, 李丽, 等. 中国大陆地震震源深度及其构造含义. 科学通报 , 2002, 47(9): 663–670. Zhang G M, Wang S Y, Li L, et al. Focal depth of continental earthquakes in China and its seismotectonic implications. Chinese Science Bulletion (in Chinese) , 2002, 47(9): 663-670. |
| [3] | 石耀霖, 朱守彪. 中国大陆震源机制深度变化反映的地壳-地幔流变特征. 地球物理学报 , 2003, 46(3): 359–365. Shi Y L, Zhu S B. Contrast of Rheology in the crust and mantle near Moho revealed by depth variation of earthquake mechanism in continental China. Chinese J. Geophys. (in Chinese) , 2003, 46(3): 359-365. |
| [4] | King R. Observations of sPn from Swabian Alb earthquakes at the GRF Array. J. Geophys. , 1979, 45: 337-340. |
| [5] | Helmberger D, Engen G. Modeling the long-period body waves from shallow earthquakes at regional ranges. Bull. Seism. Soc.Am. , 1980, 70: 1699-1714. |
| [6] | Zonno G, Kind R. Depth determination of North Italian earthquakes using Grafenberg data. Bull. Seism. Soc. Am. , 1984, 74: 1645-1659. |
| [7] | Langston C. Depth of faulting during the 1968 Meckering, Australia, earthquake sequence determined from waveform analysis of local seismograms. J. Geophys. Res. , 1987, 92: 1561-1574. |
| [8] | Langston C. The SsPmp phase in regional wave propagation. Bull. Seism. Soc. Am. , 1996, 86: 133-143. |
| [9] | Zhao L, Helmberger D. Broadband modelling along a regional shield path, Harvard recording of the Saguenay earthquake. Geophys. J. Int. , 1991, 105: 301-312. DOI:10.1111/gji.1991.105.issue-2 |
| [10] | Zhao L, Helmberger D. Source retrieval from broadband regional seismograms:Hindu Kush region. Phys. Earth Planet. Interiors , 1993, 78: 69-95. DOI:10.1016/0031-9201(93)90085-N |
| [11] | Bock G. Depth phases from local earthquakes. BMR J. Aust. Geol. Geophys. , 1993, 13: 275-279. |
| [12] | Bock G, Grunthal G, Wylegalla K. The 1985/86 Western Bohemia earthquakes:modeling source parameters with synthetic seismograms. Tectonophysics , 1996, 261: 139-146. DOI:10.1016/0040-1951(96)00062-5 |
| [13] | Zhu L, Helmberger D. Regional waveform Calibration in the Pamir-Hindu Kush region. J. Geophys. Res. , 1997, 102: 22799-22813. DOI:10.1029/97JB01855 |
| [14] | Saikia C. A method for path calibration using regional and teleseismic broadband seismograms:application to the 21 May 1997 Jabalpur, India earthquake (Mw5.8). Curr. Sci. , 2000, 79: 1301-1311. |
| [15] | Saikia C, Woods B, Thio H. Calibration of the regional crustal waveguide and the retrieval of source parameters using waveform modeling. Pure Appl. Geophys. , 2001, 158: 1301-1338. DOI:10.1007/PL00001224 |
| [16] | Bent A L, Perry C. Depths of eastern Canadian earthquakes from regional data. Seism. Res. Lett. , 2002, 73: 273-284. DOI:10.1785/gssrl.73.2.273 |
| [17] | Uski M, Hyvonen T, Korja A, et al. Focal mechanisms of three earthquakes in Finland and their relation to surface faults. Tectonophysics , 2003, 363: 141-157. DOI:10.1016/S0040-1951(02)00669-8 |
| [18] | Ma, Atkinson. Focal depths for small to moderate earthquakes (mn≥2. 8) in western Quebec, southern Ontario, and Northern New York. Bull. Seism. Soc. Am. , 2006, 96: 609-623. |
| [19] | Kim Dineva, Ma, Eaton. The 4 August 2004, Lake Ontario, Earthquake. Seism. Res. Lett. , 2006, 77: 65-73. DOI:10.1785/gssrl.77.1.65 |
| [20] | Kastrup U, Deichmann N, Fr··ohlich A. Evidence for an active fault below the northwestern Alpine foreland of Switzerland. Geophys. J. Int. , 2007, 169: 1273-1288. DOI:10.1111/gji.2007.169.issue-3 |
| [21] | 房明山, 杜安陆, 董孝平, 等. 用sPn震相测定近震震源深度. 地震地磁观测与研究 , 1995, 16(5): 13–18. Fang M S, Du A L, Dong X P, et al. Determination of focal depth with the sPn phase (in Chinese). Seismol Geomag Obser Res. (in Chinese) , 1995, 16(5): 13-18. |
| [22] | 任克新, 邹立晔, 刘瑞丰, 等. 用sPn计算内蒙地震的震源深度. 地震地磁观测与研究 , 2004, 25(3): 24–31. Ren K X, Zou L H, Liu R F, et al. Application of sPn to focal depth determination in inner Mongolia. Seismologycal and Geomagnetic Observation and Research (in Chinese) , 2004, 25(3): 24-31. |
| [23] | 洪星, 叶雯燕, 邵平荣, 等. 台湾海峡南部一次5.0级地震的sPn震相分析. 地震地磁观测与研究 , 2006, 27(1): 26–31. Hong X, Ye W Y, Shao R P, et al. Simultaneous determination of the phase sPn with multiple station records. Seismological and Geomagnetic Observation and Research (in Chinese) , 2006, 27(1): 26-31. |
| [24] | 高立新, 刘芳, 赵蒙生, 等. 用sPn震相计算震源深度的初步分析与应用. 西北地震学报 , 2007, 29(3): 213–244. Gao L X, Liu F, Zhao M S, et al. Primary analysis on the seismic source depth determination using sPn phase and its application. Northwestern Seismological Journal (in Chinese) , 2007, 29(3): 213-244. |
| [25] | Langston. An integrated study of crustal structure and regional wave propagation for southeastern missouri. Bull. Seism. Soc. Am. , 1994, 84: 105-118. |
| [26] | Aki Richards. Quantitative Seismology (Second Edition). Sausalito, CA: University Science Books, 2002 . |
| [27] | Haskell N A. Radiation pattern of surface waves from point sources in a multi-layered medium. Bull. Seism. Soc. Am. , 1964, 70: 1015-1036. |
| [28] | Wang C Y, Herrmann R B. A numerical study of P, SV, and SH-wave generation in a plane layered medium. Bull. Seism. Soc. Am. , 1980, 70: 1015-1036. |
| [29] | Zhu L, Rivera L A. A note on the dynamic and static displacements from a point source in multi-layered media. Geophys. J. Int. , 2002, 148: 619-627. DOI:10.1046/j.1365-246X.2002.01610.x |
| [30] | Magistrale H, McLaughlin K, Day S. A geology-based 3-D velocity model of the Los Angeles basin sediments. Bull. Seismol. Soc. Am. , 1996, 86: 1161-1166. |
| [31] | Chong Ni. Near surface velocity and QS structure of the Quaternary sediment in Bohai basin, China. Earthq. Sci. , 2009, 22: 451-458. DOI:10.1007/s11589-009-0451-1 |
| [32] | Brocher T M. Compressional and shear-wave velocity versus depth relations for common rock types in Northern California. Bull. Seismol. Soc. Am. , 2008, 98(2): 950-968. DOI:10.1785/0120060403 |
| [33] | 吕坚, 郑勇, 倪四道, 等. 2005年12月26日九江-瑞昌Ms5.7, Ms4.8地震的震源机制解与发震构造研究. 地球物理学报 , 2008, 51(1): 158–164. Lu J, Zheng Y, Ni S D, et al. Focal mechanisms and seismogenic structure of the Ms5.7 and Ms4.8 Jiujiang-Ruichang earthquakes of the Nov. 26, 2005.. Chinese J.Geophys (in Chinese) , 2008, 51(1): 158-164. |
| [34] | 杨中书, 曾文敬. 利用双差法对2005年江西九江-瑞昌5.7级地震序列重新定位. 地震地磁观测与研究 , 2007, 28(2): 25–31. Yang Z S, Zeng W J. Relocation of the 26 Nov 2005 Jiujiang-Ruichang 7 earthquake sequence using the double-diference earthquake location algorithm. M5. Seismological and Geomagnetic Observation and Research (in Chinese) , 2007, 28(2): 25-31. |
| [35] | Bouchon. The importance of the surface or interface P wave in near-earthquake studies. Bulletin of the Seismological Society of America , 1978, 68(5): 1293-1311. |
| [36] | Klose C D, Seeber L. Shallow Seismicity in Stable Continental Regions. Seismological Research Letters , 2007, 78: 554-562. DOI:10.1785/gssrl.78.5.554 |
 2010, Vol. 53
2010, Vol. 53