2. 中国科学院地球深部重点实验室, 北京 100029;
3. 中国科学院研究生院, 北京 100049;
4. 中国石油大学(北京) CNPC物探重点实验室, 北京 102249
2. Key Laboratory of Earth's Deep Interior, Chinese Academy of Sciences, Beijing 100029, China;
3. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
4. CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum-Beijing, Beijing 102249, China
研究复杂介质中弹性波的传播,对于利用地震波了解地下构造、评价地下流体性质、提高地震测井解释精度具有重要意义.为了深入了解地震波在真实介质中的传播机理,地震波模拟需要利用更加符合实际的介质模型[1, 2].目前广泛使用的孔隙介质弹性理论由Biot[3~5]提出,孔隙介质模型比单一的弹性固体模型更加符合实际地下储层.孔隙介质的黏滞效应源于固相与液相之间的耦合作用,并导致慢纵波的存在.虽然Biot理论在解释地震波传播特征的多个方面还存在明显不足,如尺度问题、衰减问题、速度频散等,但仍具有不可动摇的坚实地位[6].
地震波数值模拟中常用的方法包括有限差分法、有限元法[7]、边界元法[8, 9]、伪谱法[10~13]等,各有优势[14].有限差分方法简便灵活,因而在弹性介质、黏弹性介质、孔隙介质和各向异性介质模拟中得到了广泛使用[15~18].交错网格技术能有效提高计算精度,而且简便易行,在有限差分法模拟中得到广泛应用.但目前常用的普通交错网格技术(Standard StaggeredGrid,SSG)[19~21]在处理非均匀性较强的介质时需要对物性参数进行插值,可能会产生较强的数值噪音,甚至运算不稳定,另外对自由界面需要进行单独处理[22, 23].近年来发展起来的旋转交错网格技术(Rotated Staggered Grid,RSG)[24~28]将每个物理量的各个分量都定义在同一个位置,在计算空间导数时,不同于常规的SSG技术,RSG技术计算对角线方向的空间导数,然后线性内插得到坐标轴方向的空间导数近似值.
地震波模拟中的一个重要问题是吸收边界条件.由于地震波在实际介质中的传播区域是地下半无限空间,而数值模拟则是在有限区域内求解问题,会产生人工边界反射的问题.前人在这方面做出了许多杰出的工作,发展了多种不同的吸收边界.这些不同的吸收边界大致可分为两大类[1]:海绵吸收边界[29]和旁轴近似吸收边界[30].近年发展起来的完全匹配层(PML)[31~38]吸收边界就是海绵吸收边界中非常高效的一种,其基本思想是用一种不存在于现实中的特殊介质作为吸收层将外域问题截断为有界问题.PML吸收边界的特点是:截断处的链接边界是透明的(即波可以任意穿过而不引起反射),吸收层的介质必须有吸收行为(即波在其中的传播是衰减的).PML有分裂和不分裂两种实现方式[39].场分裂方法(SPML)需要对波场分量进行分裂,在分裂后的方程上施加PML吸收边界;从编程角度看由于要考虑众多PML区域,因而编程较为复杂.非场分裂方法(NPML)不需要分解场分量,但需要在时间域做大量的卷积运算,计算量较大.因此目前在波场正演中多数还是使用SPML.
常规PML吸收边界(包括SPML和NPML)在数值模拟实现时存在的一个重要问题是,离散化后的吸收边界在大角度入射时,反射系数不为零,导致有较强的能量被反射回计算区域.这主要是由于PML区域中,大角度入射的波穿透较浅,沿平行界面方向的传播距离也较大,因而不能被有效吸收.此外,目前采用的PML格式在极低频率时也会出现奇异性,导致虚假反射.针对这两个问题,近年来在微波传播计算中发展了一种无需显式卷积计算的不分裂的迭代格式完全匹配层吸收边界(CPML)[40, 41],该吸收边界条件不仅吸收效果明显、易于实现,而且比传统PML明显节省存储量,目前已被应用于有限差分方法的地震波模拟中[42~45].
本文将迭代格式的CPML吸收边界应用于孔隙弹性介质中速度-应力旋转交错网格高阶有限差分算法中,模拟孔隙介质中弹性波的传播.通过数值算例比较,其吸收效果明显优于常规PML吸收边界方法.本文分析了孔隙弹性介质CPML吸收边界参数对吸收效果的影响,据此,对CPML吸收边界参数进行了优化,极大地改善了孔隙弹性介质数值模拟中不分裂卷积完全匹配层吸收边界的应用效果.
2 Biot流体饱和孔隙介质弹性方程 2.1 Biot方程
设

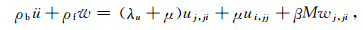
|
(1) |
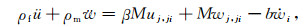
|
(2) |
其中,ρb和ρm由固体颗粒密度ρs和流体密度ρf确定:
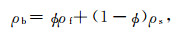
|
(3) |
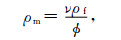
|
(4) |
其中,ν是描述孔隙结构特征的弯曲度因子.
各向同性孔隙介质中固相体积模量为Ks,液相体积模量为Kf;干岩石骨架的体积模量为Kd,剪切模量为μ.则Biot系数β,耦合模量M、饱和岩石的拉梅系数λu和黏滞系数b由下列式子给出:

|
(5) |
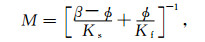
|
(6) |

|
(7) |
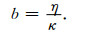
|
(8) |
其中,η是孔隙流体的黏滞系数,κ是渗透率.
对均匀孔隙弹性介质,其特征频率为
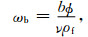
|
(9) |
当激发频率远小于特征频率时,固体骨架和孔隙流体之间的黏滞作用超过惯性作用,慢纵波表现为扩散波.
2.2 速度-应力关系
波动方程数值模拟中通常将二阶方程改写为一阶格式,如速度-应变格式[34, 49, 50]、速度-应力格式[19, 51, 52]等.本文采用速度-应力格式.令固相速度vi=


|
(10) |
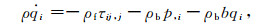
|
(11) |
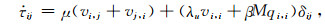
|
(12) |
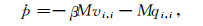
|
(13) |
其中,ρ=ρmρb-ρfρf.
对于2D问题,如上的孔隙介质弹性方程速度-应力格式的分量形式共有8个方程;3D则共有13个方程.
3 完全匹配层吸收边界完全匹配层吸收边界通过坐标扩展函数将实数空间坐标变换为复数坐标,引入一种虚拟的介质层,该层介质的波阻抗与相邻介质的波阻抗完全匹配,因而理论上入射波可以无反射的进入该层,并被完全吸收.
3.1 常规完全匹配层吸收边界引入复数因子将直角坐标扩展为复数坐标:
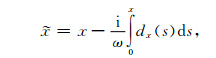
|
(14) |
其中,
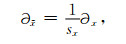
|
(15) |
其中,

|
(16) |
场分裂完全匹配层[32, 53, 54]是将方程中的空间微分算子分解为与吸收边界相垂直(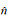
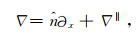
|
对分解的速度-应力格式方程在频率域内用(15)式将坐标重写,再通过逆Fourier变换回到时间域,即得到一阶SPML格式的波动方程.
以式(10)为例,2D情况下,令i=x,则分解为
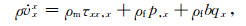
|
(17) |
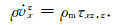
|
(18) |
变换到频率域并重写为复数坐标格式:
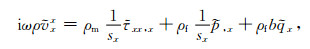
|
(19) |
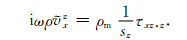
|
(20) |
逆Fourier变换到时间域:

|
(21) |
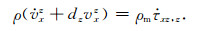
|
(22) |
常规的不分裂完全匹配层[55, 56]先在频率域用(15)式将坐标重写,然后通过逆Fourier变换回到时间域.令sx(t)为
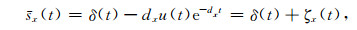
|
(23) |
式中δ(t)是单位冲激函数,u(t)是单位阶跃函数.则在时间域有
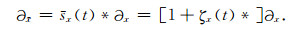
|
(24) |
同样以(10)式为例,2D情况下,令i=x,常规不分裂完全匹配层吸收边界格式为
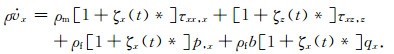
|
(25) |
可以看出场分裂完全匹配层需要对速度场和应力场进行分离,这使得方程数量变多,增加了计算复杂性和计算量;而常规不分裂完全匹配层则需要进行卷积计算,需要大量存储空间和较大的计算量.常规完全匹配层吸收边界使入射平面波Ae-(k·xi-ωt)在PML区域内xi方向以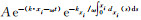
造成常规完全匹配层吸收边界对大角度入射、低频入射波和倏逝波不能有效吸收的原因之一是常规完全匹配层的扩展函数sx的极点为原点.而卷积完全匹配层通过将扩展函数sx的极点移动到复平面的虚轴上对常规完全匹配层进行了改善.本文所采用的迭代格式CPML吸收边界[40, 42~45, 56]有两个特点:(1)改造坐标扩展所用的复数因子以提高大角度和低频入射的吸收效果;(2)引入辅助变量避免通过存储过去时刻的波场信息以计算卷积的办法.因为不需要对场进行分裂,所以采用CPML时,不需要对已有的有限差分程序进行过多的修改.
首先给出经改造的扩展函数sx的形式:

|
(26) |
其中,χx≥1,αx≥0.然后分别介绍用迭代卷积法[42~44]和微分方程法[45]推导迭代格式CPML吸收边界的过程,最后给出CPML吸收边界中参数设置的一般原则.
3.2.1 迭代卷积法将(26)式代入(15)式,并做逆Fourier变换:

|
(27) |
其中sx(t)是
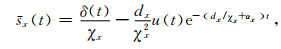
|
(28) |
令
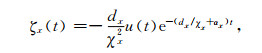
|
(29) |
于是,
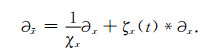
|
(30) |
在第n个时间步时,(30)式中的卷积项可写成
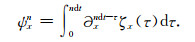
|
(31) |
(31)式进一步可写成

|
(32) |
其中,

|
(33) |
若令
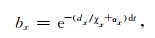
|
(34) |
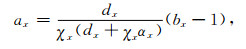
|
(35) |
则
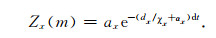
|
(36) |
因为(36)式中的Zx可以表示为指数形式,则卷积可通过如下迭代方式求解[58],

|
(37) |
本小节对文献[45]中公式推导过程进行了部分修正.
将(26)式代入(15)式,有
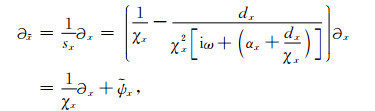
|
(38) |
其中,
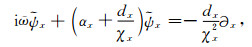
|
(39) |
对(39)式做逆Fourier变换,有:
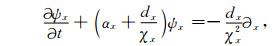
|
(40) |
其中,ψx是
形如

|
(41) |
其中,c为任意常数.将(41)式离散,得到:
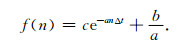
|
(42) |
通过迭代格式可将常数c消去,则有:

|
(43) |
由(43)式可知,(40)式中的ψx可由下式迭代求解:
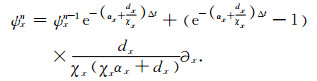
|
(44) |
由两种方法得到的ψx(见(37)式和(44)式)的迭代格式相同,但第二种方法只需求解一阶线性微分方程,过程简洁.以上两种迭代算法的初始条件应为ψx|t=0=0.
采用迭代格式的CPML在实现时,只需要一个额外的辅助变量ψx,可以极大地提高计算效率,既避免了场分解情况下的众多的方程,又不必在时间域显式的进行卷积运算.对空间导数做如下的替换即可将波动方程过渡到PML区域波动方程:

|
(45) |
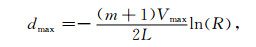
|
(46) |

|
(47) |
其中,l(0≤l≤L)为PML内的计算点到PML区域内边界的距离;L为该PML区域的厚度;m为多项式的阶数,一般取为2或3;R为理论反射系数,本文取为10-6.
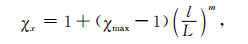
|
(48) |
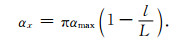
|
(49) |
当αx=0,χx=1时,sx与常规PML一致.PML区域内αx在0~αmax间线性变化,通常取αmax=f0,其中f0是子波主频.
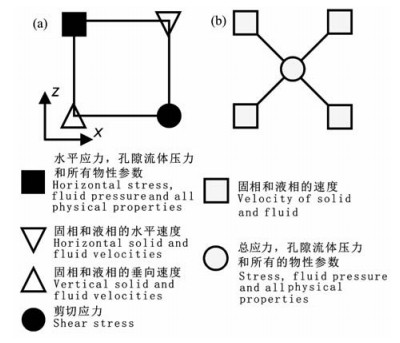
4 旋转交错网格有限差分不分裂卷积完全匹配层吸收边界的实施旋转交错网格(RSG)是近年发展起来的一种空间离散技术[23~28].旋转交错网格与普通交错网格的示意图见图 1.旋转交错网格将相同物理量定义在相同的位置(将所有的速度分量定义在一个位置,而应力分量则定义在另一个位置).通常将弹性模量等物性参数定义在应力所在位置,更新应力时无需对弹性模量等相关参数进行平均.介质密度在旋转交错网格和普通交错网格中均有两种定义方式:定义在应力处(SSG中法向应力),或定义在速度处(SSG中速度分量).若定义在速度(SSG中速度分量)所在的位置,需要在密度建模时使用相邻网格的密度进行算术平均;若定义在应力(SSG中法向应力)所在的位置,则建模时无需平均,而在更新速度时做算术平均即可.本文采用的是将密度定义在应力所在位置的办法.
|
图 1 有限差分算子示意图 (a)普通交错网格,其中方形代表τxx、τzz、p和物性参数,实心圆代表τxz,倒三角代表vx和qx,正三角代表vz和qz;(b)旋转交错网格,其中圆代表应力与物性参数,方形代表速度. Fig. 1 Stencils of finite-difference operators (a) Standard staggered grid with four grid for velocity, stress and physical properties. (b) Rotated staggered grid with only one grid for all velocity components and one for all stress components and physical properties. |
RSG技术沿空间网格的对角线方向计算空间导数,在将计算结果线性内插得到坐标轴方向的空间导数,得到网格直角坐标系下坐标轴方向的空间导数.令
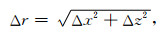
|
(50) |
则对角线方向x和z可表示为
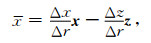
|
(51) |
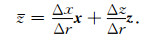
|
(52) |
直角坐标下的坐标轴方向的一阶空间导数为
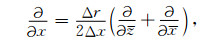
|
(53) |
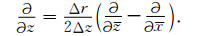
|
(54) |
下面将给出2D孔隙弹性介质速度-应力格式方程的旋转交错网格与不分裂卷积完全匹配层吸收边界的实施的详细过程:
固液相各速度及应力分量的旋转交错网格有限差分的离散格式及实施细节:
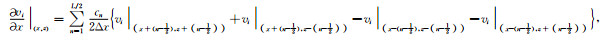
|
(55) |
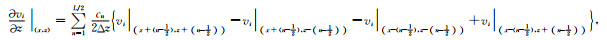
|
(56) |
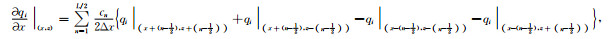
|
(57) |
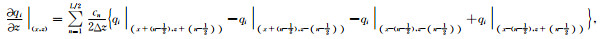
|
(58) |
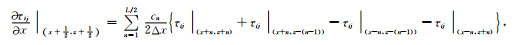
|
(59) |
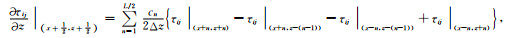
|
(60) |
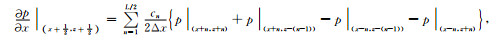
|
(61) |
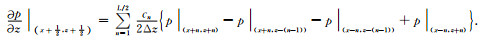
|
(62) |
其中cn是差分系数,L表示是该差分近似是L阶的.
对(55)~(62)式由(37)式求取各参数的辅助变量
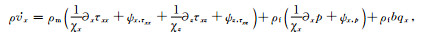
|
(63) |
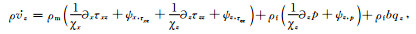
|
(64) |

|
(65) |
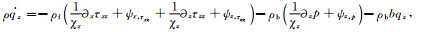
|
(66) |

|
(67) |

|
(68) |
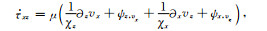
|
(69) |
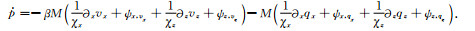
|
(70) |
本文采用时间域中心差分求解(63)~(70)式中的时间导数.
5 震源与稳定性条件 5.1 震源本文采用Gaussian函数的一阶时间导数作为震源函数:
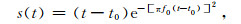
|
(71) |
其中,f0是震源主频,t0是震源函数的中心.速度-应力关系的双相介质数值模拟中的震源可以加为速度源,也可以加为应力源.双相介质模拟可以施加体源、固相源和液相源三种[34, 46].体源是将震源的能量按比例分配在固相和液相上,Wf=ϕ,Ws=(1-ϕ),Wr=ϕ|Wf-Ws|,其中Wf是液相比例,Ws是固相比例,Wr描述固体骨架与孔隙流体之间的相对运动.
5.2 稳定性条件时间域二阶精度,空间域2n阶精度均匀介质的旋转交错网格有限差分的稳定性条件[48, 52]为(假设各方向空间步长相等):

|
(72) |

|
(73) |
其中Δt是时间步长,Vmax是最大相速度,Δh是空间步长,D是空间维数,ck是旋转交错网格空间差分系数.空间八阶近似的系数[28, 59]为
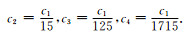
旋转交错网格有限差分的最小波长的网格数与差分的空间频散有关[23].对于空间二阶,需要最小波长网格数至少为12;四阶至少为6;八阶至少为3.最小波长的网格数的计算公式为
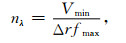
|
(74) |
其中,Vmin是最小相速度,fmax是震源的最大频率,通常取为中心频率的4倍.Δr是空间网格大小.
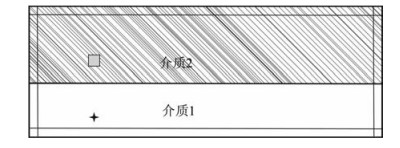
6 数值试验及分析 6.1 含孔洞双层模型考虑如图 2所示的2D含孔洞的多孔介质双层模型,模型大小:nx×nz=629×229,介质1与介质2的分界面位于iz=94处,以网格位置(ix=115,iz=134)为中心,有一长度为19个网格的正方形孔,模型四周镶嵌着厚度为14个网格的吸收边界.模型参数见表 1,震源的空间网格位置位于(ix=115,iz=34)处.经计算取Vmax=4000 m/s,Vmin=600 m/s.震源采用应力体源,震源子波采用高斯函数的一阶导数,主频为40Hz.由5.2节、(72)、(74)两式,本文取空间网格间距为0.5 m,时间间隔为0.05 ms. CP ML参数设置为m=2,R=10-6,χmax=1,αmax=40.
|
图 2 双层模型示意图 星号代表震源,灰色正方形代表孔洞,内框中的细线代表吸收边界的内部边界,较粗实线代表介质分界面. Fig. 2 Schematic diagram of a two-layer model The star indicated the location of the source, and the gray square represents the cave. The thin line inside represents the inner edge of the PML zone. The thick line represents the interface between two media. |
|
|
表 1 模型参数表 Table 1 Parameters of the two-layer model |
使用普通交错网格时需要对剪切模量进行几何平均,由于本模型的孔洞中剪切模量为零,为避免被零除,需要选择非零的较小值来替换零值,而这将影响模拟结果.因此本文不比较普通交错网格和旋转交错网格分别与完全匹配层吸收边界的组合效果,而仅比较旋转交错网格与两种不分裂完全匹配层吸收边界的组合效果.
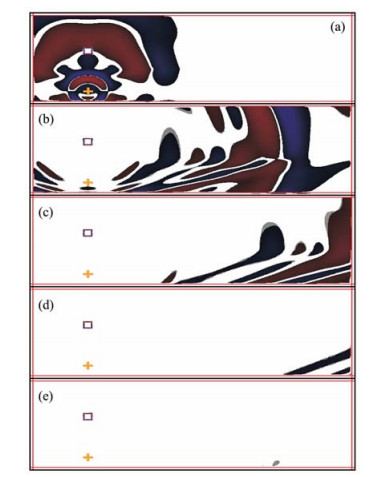
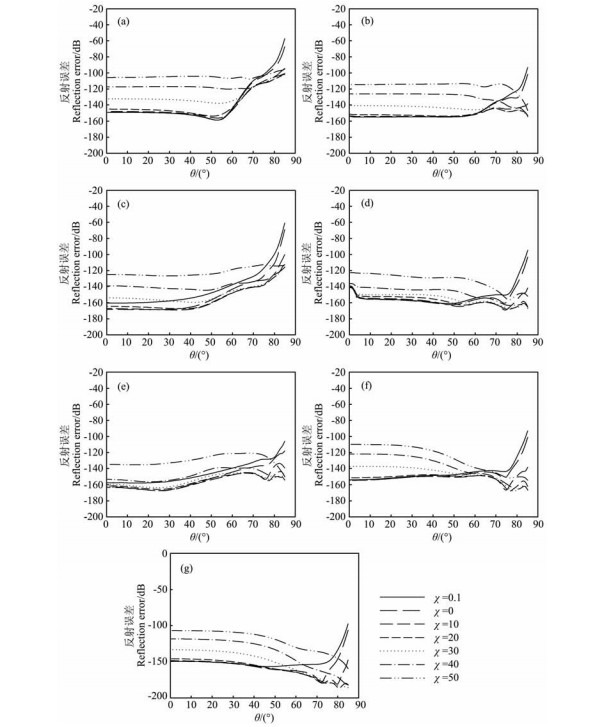
图 3和图 4是采用CPML和NPML得到的固5震源与稳定性条件相质点速度垂向分量vz在0.06 ms、0.12 ms、0.18 ms、0.24 ms和0.30 ms的快照.由图 3和图 4对比可以看出,使用NPML吸收边界会导致人工边界处出现明显的扰动(特别是大角度入射吸收边界时),而使用CPML吸收边界时在各个位置人工边界均无明显反射.造成这种差异的主要原因是这两种PML吸收边界在坐标扩展时所采用的坐标扩展函数sx不同,因此对大角度入射吸收边界波的吸收效果不同.
|
图 3 0.06 s(a)、0.12 s(b)、0.18 s(c)、0.24 s(d)、0.30 s(e)时刻,使用CPML吸收边界的固相垂向速度分量快照 咖啡色为正,蓝色为负,以使用CPML和NPML得到的相应快照中的最大值的0.5%作为切除阈值,用0.3作为归一化速度的指数以增强强弱数值的对比.十字符号代表震源,内框中的细线代表吸收边界的内部边界. Fig. 3 Snapshots of vertical component of solid velocity with CPML condition implemented, at time 0. 06 s (a), 0. 12 s (b), 0. 18 s (c), 0. 24 s (d) and 0. 30 s (e) While positive in brown and negative in blue, the value, 0. 5% of the maximum of both the snapshot of CPML and NPML, is taken as a threshold, and the normalized value is raised to the power 0. 3 to enhance small amplitudes. The cross indicated the location of the source. The thin line inside represents the inner edge of the PML zone. |

|
图 4 0.06 s(a)、0.12 s(b)、0.18 s(c)、0.24 s(d)、0.30 s(e)时刻,使用NPML吸收边界的固相垂向速度分量的快照 咖啡色为正,蓝色为负,以使用CPML和NPML得到的相应快照中的最大值的0.5%作为切除阈值,用0.3作为归一化速度的指数以增强强弱数值的对比.十字符号代表震源,内框中的细线代表吸收边界的内部边界. Fig. 4 Snapshots of vertical component of solid velocity with NPML condition implemented, at time 0. 06 s (a), 0. 12 s (b), 0. 18 s (c), 0. 24 s (d) and 0. 30 s (e) While positive in brown and negative in blue, the value, 0.5% of the maximum of both the snapshot of CPML and NPML, is taken as a threshold, and the normalized value is raised to the power 0.3 to enhance small amplitudes.The cross indicated the location of the source.The thin line inside represents the inner edge of the PML zone. |
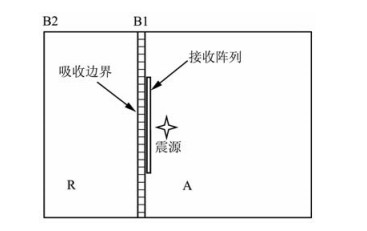
为定量比较CPML与NPML在不同角度处的吸收效果,本文对一均匀模型采用数值模拟手段,比较不同角度处检波点记录到的波形.使用参数ρs=2.250 t/m3,Ks=5.2 GPa,Kd=2.2 GPa,μ=2.4 GPa,ϕ=0.1,b=3.3×106 N·s/m4,ν=2.42,ρf=1.040 t/m3,Kf=2.25 GPa构造一个均匀模型A(如图 5所示),模型A以B1作为左边界;将模型A的左端延伸构造参考模型R(以B2为左边界);模型A和R共用右边界.模型A的网格大小为nx× nz=1229×2229,模型R的大小为nx×nz=2229× 2229,空间网格步长为0.5 m,模拟中使用的时间步长是0.1 ms,记录长度是300 ms.吸收边界厚度设为14个网格,吸收边界参数设置为m=2,R=10-6,χmax=1,αmax=40.震源位于模型R的中心(图 5星号所示),采用应力体源,子波采用高斯函数的一阶导数,主频为40Hz,距吸收边界B1右端20 m,接收阵列与B1平行,间距0.5 m,距B1右端3 m,最上面的接收点距上边界是357 m,最下面的接收点与震源在同一水平位置,在记录时间内上下边界的反射不会影响到记录的信号.接收阵列中共401个接收点,最下面的记为1号接收点,顺序标记,最上面的记为401号接收点.分别对模型A和R进行模拟,震源和接收点位置相同.对模型A,震源激发的波以不同入射角穿过接收阵列,进入吸收边界B1,由于吸收边界对这些波不能完全吸收,将有部分反射回到A中,被接收阵列记录;而对模型R,由于B1位置处没有吸收边界,因此弹性波在此处不会发生反射,B2与B1间的距离足以保证在记录时间内B2的反射不会影响记录的信号,这样得到A中接收阵列记录的信号和R中接收阵列记录的信号.
|
图 5 均匀模型示意图 Fig. 5 Schematic diagram of a homogeneous model |
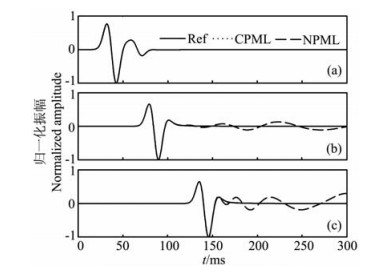
为比较吸收边界对不同角度入射波的吸收效果,在接收阵列中选取三个不同位置的接收点,比较其接收的信号.图 6是这三个接收点在模型A和模型R中记录到的固相速度水平分量,其中图 6a是1号接收点记录的信号,代表垂直入射;图 6b是201号接收点记录的信号,代表中等角度入射;图 6c是401号接收点记录的信号,代表大角度入射.图 6a中采用CPML吸收边界和采用NPML吸收边界的结果与参考模型R的结果吻合,基本没有误差.图 6b中采用CPML吸收边界的结果与参考模型R的结果吻合,而采用NPML吸收边界则出现明显的扰动.图 6c中采用CPML吸收边界的结果与参考模型R的结果吻合,而采用NPML吸收边界的结果则出现了更为明显的扰动.由图 6可以看出CPML吸收边界对各角度的入射波均有良好的吸收,而NPML吸收边界只对小角度入射波有良好的吸收,随着入射角度的增大,NPML吸收边界的吸收效果逐渐变差.
|
图 6 固相速度水平分量的波形 点线是使用CPML的结果,虚线是NPML的结果,实线是参考模型R的结果.(a)是1号接收点的记录;(b)是201号接收点的记录;(c)是401号接收点的记录.将CPML和NPML的结果与参考模型R的结果对比发现,使用NPML的结果有明显扰动现象,特别是在近切向入射的401号接收点记录中;而使用CPML的结果则与参考模型R的结果有很好的吻合. Fig. 6 Waveforms of horizontal component of solid velocity Dot line is the result of CPML in used, dashed line is the result of NPML rn used, and solid line s the result of reference model R. The top one (a) have receiver 1, the middle one (b) have receiver 201 and the bottom one (c) have receiver 401. These two, CPML and NPML, are compared with a reference model R which has the same physical parameters. Large oscillations appear in the results used NPML, especially in the record located rn 401 receiver (nearly grazing rncidence), while results with CPML have a good agreement with the reference result. |
由式(44)~(49)可知CPML中的衰减参数与最终吸收效果之间的关系复杂,为定量分析CPML中参数χmax和αmax对不同角度的吸收效果的影响,本文采用数值方法模拟计算随入射角变化的反射误差.模型与图 5所示一致.记A中第i个接收点得到的记录为si,R中相应位置的记录为Si,分别求出二者差的振幅谱和Si的振幅谱,并累加得到累加振幅谱
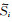

|
(75) |
考察αmax时固定χmax=1,αmax分别取0、40、80、120、160、200(即主频的0倍、1倍、2倍、3倍、4倍和5倍),各速度应力分量关于入射角度的反射误差见图 7.αmax=0,χmax=1可视为普通PML.从图 7综合来看,反射误差整体上是随入射角增大而增加的,但图 7(a,b,c,d,e,f)中在80°附近αmax=0的反射误差开始减小.综合图 7的结果可以看出αmax取0的反射误差明显较大,取160、200的反射误差相对较大,而αmax取40、80的反射误差则相对较小.在图 7(a,b,d,f)中αmax取40、80的结果比较接近,而图 7(c,e,g)中αmax取40时反射误差更小.综合图 7结果,αmax取40(即主频)是本例中的较优结果,可以得到满意的吸收效果.
|
图 7 不同αmax得到的不同分量的反射误差 (a)液相速度水平分量;(b)液相速度垂直分量;(c)固相速度水平分量;(d)固相速度垂直分量;(e)水平应力;(f)垂直应力;(g)孔隙流体压力. Fig. 7 Reflection error of different components of the solid/fluid velocity/stress with different amax (a) Represents horizontal component of fluid velocity; (b) Represents vertical component of fluid velocity; (c) Represents horizontal component of solid velocity; (d) Represents vertical component of solid velocity; (e) Represents horizontal stress; (f) Represents vertical stress; (g) Represents luid pressure. |
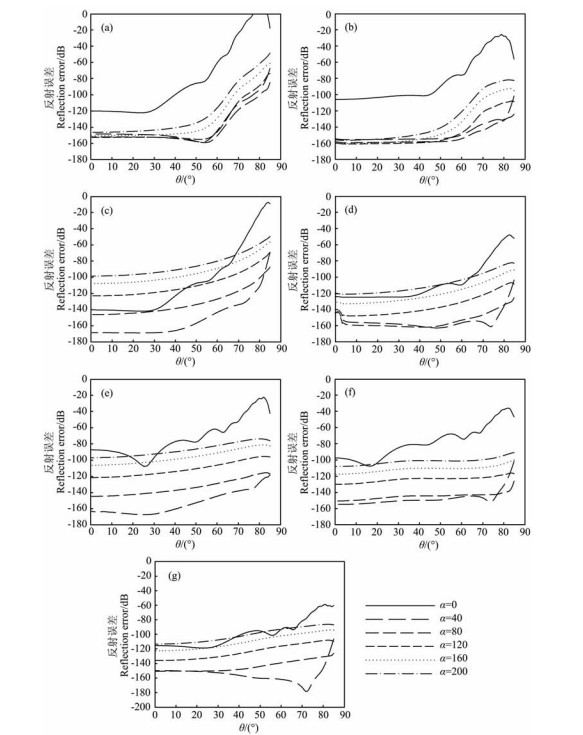
考察χmax时固定αmax=40,χmax分别取0.1、1、10、20、30、40和50,结果如图 8所示.可以看出当入射角小于60°时,χmax取50的反射误差明显最大,而χmax取0.1、1、10、20时的反射误差相近;当入射角度继续增大时,χmax取0.1和1的反射误差开始相继增大,在此角度范围χmax取10、20、30、40的反射误差相对较小.综合图 8结果来看,χmax取20是本例中的最优结果,而χmax取50的结果则是相对最差的.若仅考虑小到中等角度入射,则χmax在0.1~20之间都可以得到满意的吸收结果.
|
图 8 不同χmax得到的不同分量的反射误差 (a)液相速度水平分量;(b)液相速度垂直分量;(c)固相速度水平分量;(d)固相速度垂直分量;(e)总应力水平分量;(f)总应力垂直分量;(g)孔隙流体压力. Fig. 8 Reflection error of different components of the solid/fluid velocity/stress with different χmax (a) Represents horizontal component of fluid velocity; (b) Represents vertical component of fluid velocity; (c) Represents horizontal component of solid velocity; (d) Represents vertical component of solid velocity; (e) Represents horizontal component of stress; (f) Represents vertical component of stress; (g) Represents fluid pressure. |
由图 7和图 8可以看出αmax和χmax对CPML吸收效果的影响较为复杂,αmax对CPML吸收效果的影响要大于χmax.由前文的分析可知,当αmax=40(即αmax=f0),χmax在0.1~20之间取值时,可以使CPML得到满意的吸收效果.因此,使用CPML进行数值模拟时,可以将αmax=f0和χmax=1作为一组可接受的优化参数组合使用,其吸收效果优于常规的PML吸收边界.
7 结论常规完全匹配层吸收边界(SPML和NPML)存在吸收不彻底、计算公式复杂等缺点,针对这些缺点,在微波计算领域发展了一种无需场分裂的迭代格式卷积完全匹配层吸收边界(CPML).本文将这一方法应用到Biot方程速度-应力格式的旋转交错网格有限差分的孔隙弹性介质地震数值模拟中,详细介绍了SPML、NPML和CPML的公式推导,及CPML与旋转交错网格有限差分结合的方法.通过NPML和CPML吸收边界的数值对比分析,可以看出NPML存在边界吸收不彻底(特别是近切向入射处),而CPML能够有效降低虚假反射.使用数值模拟手段详细分析了CPML的两个重要参数χmax和αmax对边界吸收效果的影响,结果表明一般情况下χmax取值在0.1~20之间和αmax=f0即可达到较好的吸收效果.考虑到实际数值模拟时不便对同一模型进行大量不同参数组合的实验,因此αmax=f0和χmax=1是一个可接受的优化参数组合.
虽然同样精度要求下旋转交错网格间距比普通交错网格要大,但其物理意义更加准确,无需对模量等物性参数进行插值.而且对于含孔洞或裂缝等强对比的介质,旋转交错网格无需特殊处理即可得到正确结果.
本文将CPML技术与旋转交错网格有限差分技术结合,充分发挥了不同技术的优点,结果表明这一组合对人工边界反射的吸收优于目前常用的完全匹配层吸收边界,并且能满足强对比介质的模拟需要.
| [1] | Carcione J M. Wave fields in real media:wave propagation in anisotropic, anelastic, porous and electromagnetic media. Elsevier, 2007 . |
| [2] | 牟永光, 裴正林. 三维复杂介质地震数值模拟. 北京: 石油工业出版社, 2005 . Mou Y G, Pei Z L. Seismic Numerical Modeling for 3-D Complex Media (in Chinese). Beijing: Petroleum Industry Press, 2005 . |
| [3] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid.I. Low-frequency range. The Journal of the Acoustical Society of America , 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [4] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. Higher frequency range. The Journal of the Acoustical Society of America , 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [5] | Biot M A. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics , 1962, 33(4): 1482-1498. DOI:10.1063/1.1728759 |
| [6] | Mavko G, Mukerji T, Dvorkin J. The rock physics handbook. Cambridge University Press, 1998 . |
| [7] | Seron F J, Sanz F J, Kindelan M, et al. Finite-element method for elastic wave propagation. Communications in Applied Numerical Methods , 1990, 6(5): 359-368. DOI:10.1002/(ISSN)1555-2047 |
| [8] | 符力耘, 牟永光. 弹性波边界元法正演模拟. 地球物理学报 , 1994, 37(4): 521–529. Fu L Y, Mou Y G. Boundary element method for elastic wave forward modeling. Chinese J. Geophys (in Chinese) , 1994, 37(4): 521-529. |
| [9] | 胡善政, 符力耘, 裴正林. 流体饱和多孔隙介质弹性波方程边界元解法研究. 地球物理学报 , 2009, 52(9): 2364–2369. Hu S Z, Fu L Y, Pei Z L. A boundary element method for the 2-D wave equation in fluid-saturated porous media. Chinese J. Geophys (in Chinese) , 2009, 52(9): 2364-2369. |
| [10] | Gazdag J. Modeling of the acoustic wave equation with transform methods. Geophysics , 1981, 46(6): 854-859. DOI:10.1190/1.1441223 |
| [11] | Kosloff D, Baysal E. Forward modeling by a Fourier method. Geophysics , 1982, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
| [12] | Faccioli E, Maggio F, Paolucci R, et al. 2d and 3D elastic wave propagation by a pseudo-spectral domain decomposition method. Journal of Seismology , 1997, 1(3): 237-251. DOI:10.1023/A:1009758820546 |
| [13] | Mikhailenko B G, Mikhailov a A, Reshetova G V. Numerical Modeling of Transient Seismic Fields in Viscoelastic Media Based on the Laguerre Spectral Method. Pure and Applied Geophysics , 2003, 160(7): 1207-1224. DOI:10.1007/s000240300002 |
| [14] | Marfurt K J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics , 1984, 49(5): 533-549. DOI:10.1190/1.1441689 |
| [15] | Jo C H, Shin C S, Suh J H. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator. Geophysics , 1996, 61(2): 529-537. DOI:10.1190/1.1443979 |
| [16] | Wenzlau F, Müller T M. Finite-difference modeling of wave propagation and diffusion in poroelastic media. Geophysics , 2009, 74(4): T55-T66. DOI:10.1190/1.3122928 |
| [17] | Wu C, Harris J M, Nihei K T, et al. Two-dimensional finite-difference seismic modeling of an open fluid-filled fracture:Comparison of thin-layer and linear-slip models. Geophysics , 2005, 70(4): T57-T62. DOI:10.1190/1.1988187 |
| [18] | Yao Z, Margrave G F. Fourth-order finite-difference scheme for P and SV wave propagation in 2D transversely isotropic media. CREWES Research Report , 1999, 11. |
| [19] | Virieux J. P-SV wave propagation in heterogeneous media:velocity-stress finite-difference method. Geophysics , 1986, 51(4): 889-901. DOI:10.1190/1.1442147 |
| [20] | Levander a R. Fourth-order finite-difference P-SV seismograms. Geophysics , 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [21] | Sheen D H, Tuncay K, Baag C E, et al. Parallel implementation of a velocity-stress staggered-grid finite-difference method for 2-D poroelastic wave propagation. Computers and Geosciences , 2006, 32(8): 1182-1191. DOI:10.1016/j.cageo.2005.11.001 |
| [22] | Moczo P, Kristek J, Vavrycuk V, et al. 3D Heterogeneous Staggered-Grid Finite-Difference Modeling of Seismic Motion with Volume Harmonic and Arithmetic Averaging of Elastic Moduli and Densities. Bulletin of the Seismological Society of America , 2002, 92(8): 3042-3066. DOI:10.1785/0120010167 |
| [23] | 陈浩, 王秀明, 赵海波. 旋转交错网格有限差分及其完全匹配层吸收边界条件. 科学通报 , 2006, 51(17): 1985–1994. Chen H, Wang X M, Zhao H B. A rotated staggered grid finite-difference with the absorbing boundary condition of a perfectly matched layer. Chinese Science Bulletin (in Chinese) , 2006, 51(17): 1985-1994. |
| [24] | Saenger E H, Gold N, Shapiro S A. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion , 2000, 31(1): 77-92. DOI:10.1016/S0165-2125(99)00023-2 |
| [25] | Saenger E H, Shapiro S A. Effective velocities in fractured media:a numerical study using the rotated staggered finite-difference grid. Geophysical Prospecting , 2002, 50(2): 183-194. DOI:10.1046/j.1365-2478.2002.00309.x |
| [26] | Saenger E H, Bohlen T. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid. Geophysics , 2004, 69(2): 583-591. DOI:10.1190/1.1707078 |
| [27] | Saenger E H, Ciz R, Krüger O S, et al. Finite-difference modeling of wave propagation on microscale:a snapshot of the work in progress. Geophysics , 2007, 72(5): SM293-SM300. DOI:10.1190/1.2753552 |
| [28] | Wang X M, Dodds K, Zhao H B. An improved high-order rotated staggered finite-difference algorithm for simulating elastic waves in heterogeneous viscoelastic/anisotropic media. Exploration Geophysics , 2006, 37(2): 160-174. DOI:10.1071/EG06160 |
| [29] | Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics , 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [30] | Keys R G. Absorbing boundary conditions for acoustic media. Geophysics , 1985, 50(6): 892-902. DOI:10.1190/1.1441969 |
| [31] | Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics , 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [32] | Collino F, Monk P B. Optimizing the perfectly matched layer. Computer Methods in Applied Mechanics and Engineering , 1998, 164(1-2): 157-171. DOI:10.1016/S0045-7825(98)00052-8 |
| [33] | 刘顺坤, 陈向跃, 聂鑫. 有耗介质空间完全匹配层吸收边界条件及其应用. 强激光与粒子束 , 2009, 21(11): 1701–1704. Liu S K, Chen X Y, Nie X. Perfectly matched layer absorbing boundary condition and its application in truncation of lossy media space. High Power Laser and Particle Beams (in Chinese) , 2009, 21(11): 1701-1704. |
| [34] | Zeng Y Q, Liu Q H. A staggered-grid finite-difference method with perfectly matched layers for poroelastic wave equations. The Journal of the Acoustical Society of America , 2001, 109(6): 2571-2580. DOI:10.1121/1.1369783 |
| [35] | Komatitsch D, Tromp J. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophysical Journal International , 2003, 154(1): 146-153. DOI:10.1046/j.1365-246X.2003.01950.x |
| [36] | Marcinkovich C, Olsen K. On the implementation of perfectly matched layers in a three-dimensional fourth-order velocity-stress finite difference scheme. Journal of Geophysical Research-Solid Earth , 2003, 108(B5): 2276-2291. |
| [37] | 赵海波, 王秀明, 王东, 等. 完全匹配层吸收边界在孔隙介质弹性波模拟中的应用. 地球物理学报 , 2007, 50(2): 581–591. Zhao H B, Wang X M, Wang D, et al. Application of the boundary absorption using a perfectly matched layer for elastic wave simulation in poroelastic media. Chinese J. Geophys (in Chinese) , 2007, 50(2): 581-591. |
| [38] | 陈可洋. 声波完全匹配层吸收边界条件的改进算法. 石油物探 , 2009, 48(1): 76–79. Chen K Y. The improved algorithm of the perfectly matched layer absorbing boundary for acoustic wave. Geophysical Prospecting for Petroleum (in Chinese) , 2009, 48(1): 76-79. |
| [39] | Kristek J, Moczo P, Galis M. A brief summary of some PML formulations and discretizations for the velocity-stress equation of seismic motion. Studia Geophysica et Geodaetica , 2009, 53(4): 459-474. DOI:10.1007/s11200-009-0034-6 |
| [40] | Roden J A, Gedney S D. Convolutional PML (CPML):An efficient FDTD implementation of the CFS-PML for arbitrary media. Microwave and Optical Technology Letters , 2000, 27(5): 334-338. DOI:10.1002/(ISSN)1098-2760 |
| [41] | 姜永金, 毛钧杰, 柴舜连. CFS-PML边界条件在PSTD算法中的实现与性能分析. 微波学报 , 2004, 20(4): 36–39. Jiang Y J, Mao J J, Chai S L. Implementation and Analysis of the Perfectly Matched Layer Media with CFS for the PSTD Method. Journal of Microwaves (in Chinese) , 2004, 20(4): 36-39. |
| [42] | Komatitsch D, Martin R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics , 2007, 72(5): SM155-SM167. DOI:10.1190/1.2757586 |
| [43] | Martin R, Komatitsch D, Ezziani A. An unsplit convolutional perfectly matched layer improved at grazing incidence for seismic wave propagation in poroelastic media. Geophysics , 2008, 73(4): T51-T61. DOI:10.1190/1.2939484 |
| [44] | Martin R, Komatitsch D. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation. Geophysical Journal International , 2009, 179(1): 333-344. DOI:10.1111/gji.2009.179.issue-1 |
| [45] | Qin Z, Lu M H, Zhang X D, et al. The implementation of an improved NPML absorbing boundary condition in elastic wave modeling. Applied Geophysics , 2009, 6(2): 113-121. DOI:10.1007/s11770-009-0012-3 |
| [46] | Carcione J, Quiroga-Goode G. Some aspects of the physics and numerical modeling of Biot compressional waves. Journal of Computational Acoustics , 1995, 3(4): 261-280. DOI:10.1142/S0218396X95000136 |
| [47] | Zhao H B, Wang X M, Chen H. A method of solving the stiffness problem in Biot's poroelastic equations using a staggered high-order finite-difference. Chinese Physics , 2006, 15(12): 2819-2827. DOI:10.1088/1009-1963/15/12/009 |
| [48] | Masson Y J, Pride S R, Nihei K T. Finite difference modeling of Biot's poroelastic equations at seismic frequencies. Journal of Geophysical Research (Solid Earth) , 2006, 111(B10): 10305. DOI:10.1029/2006JB004366 |
| [49] | Zeng Y, Liu Q. Acoustic detection of buried objects in 3-D fluid saturated porous media:numerical modeling. IEEE Transactions on Geoscience and Remote Sensing , 2001, 39(6): 1165-1173. DOI:10.1109/36.927434 |
| [50] | Zeng Y Q, He J Q, Liu Q H. The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media. Geophysics , 2001, 66(4): 1258-1266. DOI:10.1190/1.1487073 |
| [51] | Masson Y J, Pride S R. Poroelastic finite difference modeling of seismic attenuation and dispersion due to mesoscopic-scale heterogeneity. Journal of Geophysical Research-Solid Earth , 2007, 112(B3): B03204. |
| [52] | Wenzlau F, Müller T M. Finite-difference modeling of wave propagation and diffusion in poroelastic media. Geophysics , 2009, 74(4): T55-T66. DOI:10.1190/1.3122928 |
| [53] | Chew W C, Weedon W H. A 3-D perfectly matched medium from modified Maxwell's equations with stretched coordinates. Microwave and Optical Technology Letters , 1994, 7(13): 599-604. DOI:10.1002/(ISSN)1098-2760 |
| [54] | Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics , 2001, 66(1): 294-307. DOI:10.1190/1.1444908 |
| [55] | Song R L, Ma J, Wang K X. The application of the nonsplitting perfectly matched layer in numerical modeling of wave propagation in poroelastic media. Applied Geophysics , 2005, 2(4): 216-222. DOI:10.1007/s11770-005-0027-3 |
| [56] | Wang T, Tang X M. Finite-difference modeling of elastic wave propagation:A nonsplitting perfectly matched layer approach. Geophysics , 2003, 68(5): 1749-1755. DOI:10.1190/1.1620648 |
| [57] | Drossaert F H, Giannopoulos A. Complex frequency shifted convolution PML for FDTD modelling of elastic waves. Wave Motion , 2007, 44(7-8): 593-604. DOI:10.1016/j.wavemoti.2007.03.003 |
| [58] | Luebbers R J, Hunsberger F. FDTD for N th-order dispersive media. IEEE transactions on Antennas and Propagation , 1992, 40(11): 1297-1301. DOI:10.1109/8.202707 |
| [59] | Kindelan M, Kamel A, Sguazzero P. On the construction and efficiency of staggered numerical differentiators for the wave equation. Geophysics , 1990, 55(1): 107-110. DOI:10.1190/1.1442763 |
 2010, Vol. 53
2010, Vol. 53