地球物理学报  2010, Vol. 53 Issue (10): 2442-2451   PDF    
引用本文
毛剑, 吴如山, 高静怀. 利用局部谐和基小波束的高精度叠前深度域偏移成像方法研究. 地球物理学报, 2010, 53(10): 2442-2451, doi: 10.3969/j.issn.0001-5733.2010.10.018.  
Mao J, Wu R S, Gao J H. High-accuracy prestack depth migration and imaging using local harmonic basis beamlet. Chinese J. Geophys. (in Chinese), 2010, 53(10): 2442-2451, doi: 10.3969/j.issn.0001-5733.2010.10.018.  
利用局部谐和基小波束的高精度叠前深度域偏移成像方法研究
毛剑1,2 , 吴如山2 , 高静怀1     
1. 西安交通大学电子与信息工程学院波动与信息研究所, 西安 710049;
2. Modeling and Imaging Laboratory, University of California, Santa Cruz 95064, U.S.A
收稿日期 2009-12-21, 2010-09-21 收修定稿
基金项目: 国家自然科学基金重点项目(40730424), 国家自然科学基金面上项目(40674064), 国家"863"高技术项目(2006AA09A102)和WTOPI Consortium in University of California Santa Cruz资助
作者简介: 毛剑, 男, 1980年生, 在读博士研究生, 主要从事复杂介质中地震波传播与成像及地震资料处理的理论与方法等研究.E-mail:arrowspirit@gmail.com
通讯作者: 高静怀, 男, 1960年生, 教授, 博士生导师, 主要从事地震波传播、成像、地震资料处理及信号处理方面的研究.E-mail:jhgao@mail.xjtu.edu.cn
摘要: 小波束域利用局部余弦基(local cosine bases)的偏移成像方法具有很高的计算效率和成像质量.然而局部余弦基小波束通常沿垂直方向具有两个对称波瓣.由于缺乏单一定义的方向性, 在某些强变速介质中利用局部余弦基的波传播方法会产生一定的误差, 同时也使得一些在局部角度域的操作变得非常不便.于是我们提出了利用局部谐和基进行波场外推的方法.局部谐和基(local harmonic base)是由局部余弦基和局部正弦基线性组合而成, 具有单一定义的方向性, 同时具备快速算法.局部谐和基与Gabor-Daubechies标架类似, 都具有单一定义的方向性, 但比Gabor-Daubechies标架效率更高.局部谐和基保持了与局部余弦基的偏移成像方法相同的计算效率, 但在成像精度上有了显著的提高.通过二维SEG/EAGE模型和BP模型的叠前深度域偏移成像说明了该方法的有效性.
关键词: 局部余弦基      局部谐和基      小波束      局部角度域      叠前      深度域偏移      成像     
High-accuracy prestack depth migration and imaging using local harmonic basis beamlet
MAO Jian1,2, WU Ru-Shan2, GAO Jing-Huai1     
1. Institute of Wave and Information, School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
2. Modeling and Imaging Laboratory, University of California, Santa Cruz 95064, U. S. A
Abstract: Beamlet migration using local cosine bases (LCB) has good image quality and high computational efficiency. However, local cosine beamlets have two symmetric lobes with respect to the vertical axis. This lack of uniquely defined direction-localization leads to inaccurate modeling of wave propagation in high contrast heterogeneous media, and is inconvenient for many operations in local angle domain. We proposed a new wavefield decomposition scheme using local harmonic bases (LHB), which is implemented by linear combinations of local cosine and local sine bases. Compared to Gabor-Daubechies frame (GDF) beamlet, LHB beamlet is much more efficient because LHB is still orthogonal and has fast algorithm, but it has directional localization which is similar with GDF. On the other hand, beamlet migration using LHB propagators has the same efficiency as LCB propagator but improves the accuracy due to the directional localization built in the propagators. The results of prestack depth migration using the synthetic data of the 2D SEG/EAGE salt model and 2D BP benchmark model demonstrate the good imaging quality and the ability of direction localization..
Key words: Local cosine basis      Local harmonic basis      Beamlet      Local angle domain      Prestack      Depth migration      Imaging     
1 引言

基于波动方程在双域（如空间-波数域）进行偏移的方法对解决横向变速问题具有较高的精度，同时也因为快速傅里叶变换（FFT）的使用使其具有很高的效率.其中常用的双域方法有：相移加插值方法（phase shift plus interpolation）[1]，相位屏方法（phase screen）[2, 3]，傅里叶有限差分方法（Fourier finite-frequency）[4, 5]和分裂傅里叶方法（split-step Fourier）[6, 7]等.然而对具有强速度反差的模型（如盐丘模型）的偏移成像仍然存在一些问题.通常双域方法将速度模型在每一个深度分解成背景速度和扰动速度，这里背景速度和扰动速度都是全局性的.偏移的过程首先是基于均匀背景介质对波数域的波场进行相移，然后再用扰动速度在空间域对波场进行相位修正.因为速度扰动是全局性的，所以有可能带来较大的误差.另一方面，波场的大角度分量的传播（陡倾角结构的成像）在这种方法下也很难处理.

为了提高在强变速介质中波场偏移的精度，同时利用空间和波数域局部化性质的方法取得了很多的进展，小波束（beamlet）偏移方法[8~10]就是其中的一种.小波束方法是基于波动方程利用小波变换和局部扰动理论提出的一种偏移方法，其中主要有利用Gabor-Daubechies标架[8, 9]和利用局部余弦基[10]分解两种方法.利用小波束方法进行偏移，首先波场在相同长度的窗口划分下分解为关于局部波数具有局部方向性的小波束，然后每一个深度的波场通过基于局部扰动理论得到的小波束传播算子（稀疏传播算子矩阵）作用进行传播.由于利用了局部化特性，小波束偏移方法在处理强变速介质时具有较大的优势，在偏移精度和成像质量上相对以前的方法都有了较大的改进，并且在计算效率上相当.

但现有的小波束偏移方法也存在一些问题. Gabor-Daubechies标架分解完备但非正交，因此是具有冗余度的分解，从而导致计算效率较低.局部余弦基满足正交分解并且具有快速算法，并已经成功地用于不同数据体的偏移成像.然而局部余弦小波束通常有两个对称的波瓣，使其不具备方向性.这种单一方向性的缺乏使其传播精度受到了一定的影响，同时也限制了其在局部角度域的应用.虽然Gabor-Daubechies标架偏移方法计算效率较低（计算时间通常是局部余弦基方法的4~5倍），但它在偏移过程中提供了局部角度域的信息，从而可以很方便地用于校正探测系统的孔径效应及其他一些角度相关的滤波处理.于是我们提出了利用局部谐和基[11]进行小波束偏移的方法，这种方法通过局部余弦基和局部正弦基的线性组合实现，它与局部余弦基偏移方法具有相同的计算效率但同时又在传播算子中引入了方向性.

本文第2节主要介绍局部谐和基的基本理论；第3节推导了在单程波方程下基于局部谐和基的波场传播算子；第4节通过一些模型（如横向变速模型、二维SEG/EAGE模型、二维BP模型）的偏移成像结果说明了该方法的有效性和适用性.

2 局部谐和基 2.1 局部余弦/正弦基

Balian-Low定理[12]证明高斯窗调制的指数函数不能构成有很好频率局部化特性的基.然而Coifman和Meyer[13]成功地利用光滑交叠的钟形函数（bell function）调制余弦/正弦函数构造了局部余弦/正弦基[14, 15].局部余弦/正弦基可统一称为局部三角基（local trigonometric bases），具有正交性和很好的局部化特性（较小的Heisenberg盒）.局部余弦变换与窗口傅里叶变换（Window Fourier Transform）非常类似，但其正交性和快速算法使其在用于波场分解和传播时具有较高的效率.

局部余弦/正弦基函数（local cosine/sine basis）的定义如下

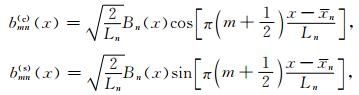
(1)

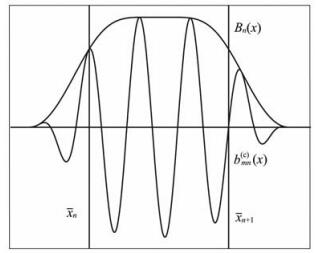
bmn（c）（x）和bmn（s）（x）分别代表局部余弦基和局部正弦基（如图 1所示）.其中xn为第n个区间起始位置，Ln=xn+1 -xn为区间长度，m为波数指标，钟形窗函数Bn（x）是定义在紧支集[xn-ε，xn+1+ε′]上的光滑函数，并且xn+ε≤xn+1 -ε′，ε，ε′分别为区间左边、右边的重叠半径.

图 1 局部余弦基函数 Fig. 1 Local cosine basis

从公式（1）看出，局部正弦基是由调制的谐函数构成，因此非常适用于波场分解.并且由于其正交性，波场分解的系数具有稀疏性.局部余弦基算子也已经被证明是一种精确高效的单程波传播算子.但局部正弦/余弦基不具有单一方向性，即在波数域有两个对称的波瓣.令ξm=π（m+1/2）/Ln为局部横向波数（local horizontal wavenumber），局部余弦基函数可表示为

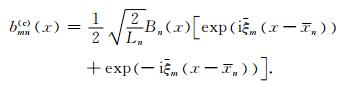
(2)

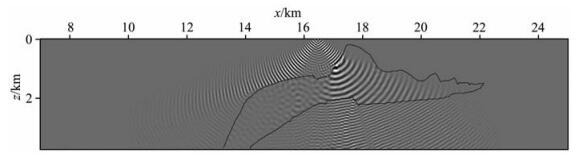
公式（2）中的两个指数项表明局部余弦基小波束有两个对称的波瓣，即沿关于z轴对称的两个方向传播.图 2给出了单个局部余弦小波束在二维SEG/EAGE盐丘模型中传播的情况.正是因为缺乏单一的方向性，局部余弦和正弦基在处理强变速介质问题时有一定误差，此外也不能用于局部角度域的操作（如方向性照明分析、探测孔径效应校正等）.因此，为了提高传播精度同时引入方向性以便在角度域进行操作，我们引入利用局部谐和基和局部指数标架LEF（local exponential frame）的波场分解方法.前者为完备正交基，适用于波场的分解和传播，具有单一方向性定义；后者为紧标架，具有冗余度，提供了全部的角度域信息，我们在下一节讨论二者的区别，局部指数标架在角度域的方向照明分析将在另一篇文章中详细讨论.

图 2 单个局部余弦小波束在二维SEG/EAGE模型中的传播 Fig. 2 A singee local cosine beamlet propagation in SEG/EAGE model
2.2 局部谐和基

局部谐和基LHB的定义为

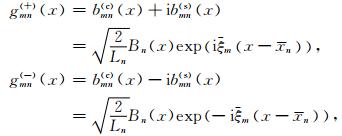
(3)

其中m=0，1，…，M-1，ξm为局部波数.gmn（+）（x）和gmn（-）（x）分别称为右传播和左传播局部谐和基小波束.图 3给出了单个局部谐和基小波束在二维SEG/EAGE模型中传播的情况，从图中可以看到该小波束具有单一的方向性.利用局部谐和基对复数波场进行分解，首先对复数波场的实部用局部余弦基分解，然后对复数波场的虚部进行分解，最后将两组系数线性组合即可得到局部谐和基的分解系数，我们在后面将给出详细的波场分解公式.由于局部谐和基的分解系数为实数，不携带相位信息，因此在用于方向照明分析时我们需要回到局部指数标架的表示以提供全部的角度域信息.局部指数标架为冗余度为2的紧标架，其基函数表达式与局部谐和基相同，但分解系数为复数系数.局部谐和基具有单一定义的方向性，同时也是没有冗余度的正交基，因此提供了一种准确高效的波场分解和传播方法.

图 3 单个局部谐和基小波束在二维SEG/EAGE模型中的传播 (a)左传局部谐和基小波束; (b)右传局部谐和基小波束. Fig. 3 Single local harmonic beamlet propagation in SEG/EAGE model (a) Lett-propagating local harmonic beamlet; (b) Right-propagating local harmonic beamlet.
3 小波束域利用局部谐和基的偏移成像方法 3.1 利用局部谐和基处理单程波方程

频率-空间域的标量波波动方程表达式如下

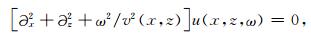
(4)

其中ω为角频率，v（x，z）为速度，u（x，z，ω）则代表频率域波场.

深度z处的波场可以沿x轴分解到小波束域

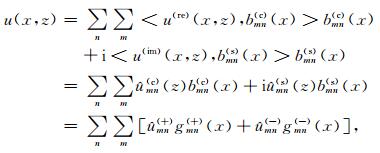
(5)

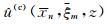
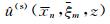
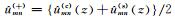
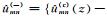
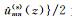
其中u（re）（x，z）和u（im）（x，z）分别为复波场的实部和虚部，bmn（c）（x）和bmn（s）（x）分别为关于局部余弦基和局部正弦基小波束，和分别为关于局部余弦基和局部正弦基小波束的分解系数.这里我们对波场的实部和虚部分别进行局部余弦分解和局部正弦分解以获得方向性，这和用局部指数标架小波束分解在形式上类似，但由于分解系数和为实数，所以这里的分解仍然是正交分解.

将波场的分解式（5）代入式（4）的波动方程可得

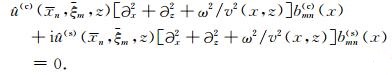
(6)

由于实部和虚部系数的任意性，从而有bmn（c）（x）和bmn（s）（x）必须都满足波动方程.通过单程波近似，我们可以得到小波束的演化表达式如下

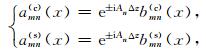
(7)

其中amn（c）（x）（amn（s）（x））为bmn（c）（x）（bmn（s）（x））在非均匀介质中传播演化后的波场函数，An为平方根算子，

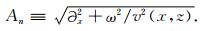
(8)

这里我们假设波场u（x，z）为能量归一化的单向传播（向下传播）的波场，所以无需考虑传播时的幅度.当重新回到波场表示进行成像或者正演时，我们可以通过幅度校正因子恢复得到正确的幅度.因为amn（c）（x）和amn（s）（x）是经过传播演化后的波场函数，所以它们不再是小波束.接下来我们通过局部扰动理论得到amn（c）（x）和amn（s）（x）的解.

3.2 局部扰动近似下小波束域的单程波传播算子 3.2.1 局部扰动近似

在局部扰动近似[16]中对每一个位于xn的窗口选取局部参考速度v0（xn，z），从而通过局部参考速度算出局部扰动.一般对具有横向变速的速度模型，局部扰动较小，因此我们只考虑一阶近似，也就是对每个窗口采用相位屏近似进行相位校正.这意味着对平方根算子或者拟微分算子进行近似[8, 9]

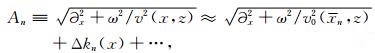
(9)

其中Δkn（x）=ω（1/v（x，z）-1/v0（xn，z））即为局部扰动项.

小波束演化表达式可以近似为一个双域表达式（拟微分算子的薄层近似）

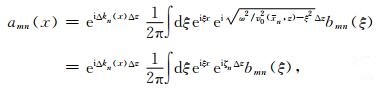
(10)

这里amn（x）代表3.1节公式（7）提到的amn（c）（x）和amn（s）（x），式中

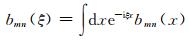
(11)

为波数域基函数，ξ为水平波数，

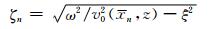
(12)

为垂直波数.从（10）式可以看出小波束的演化是通过算子分裂近似后在双域内执行.等式右边第一个乘积项为空间域的相位屏校正因子，第二项则是利用局部背景速度在波数域的相移因子.

由（10）式直接进行小波束演化属于全局操作，因此需要较大的计算量.对每一个小波束而言，需要一次在波数域的全局的相移操作，再加上一个空间域的相位屏校正.传播后的波场可以通过将所有小波束的贡献叠加在一起得到.这在操作上与相移加插值PSPI[1]，非平稳相移NSPS[17]以及广义PSPI[18]十分类似.接下来，我们将针对（10）式讨论一种有效的实现算法.

3.2.2 小波束域单向波传播算子

基于（10）式的双域表达式，我们定义

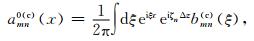
(13)

和

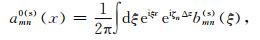
(14)

为在局部背景速度v0（xn，z）下演化后的小波束. amn0（c）（x）和amn0（s）（x）经过传播后将不再是原先的小波束，因此需要重新进行小波束分解，并且经过传播后的amn0（c）（x）和amn0（s）（x）将不再是实数.

我们对amn0（c）（x）和amn0（s）（x）的实部和虚部分别用局部余弦基和局部正弦基重新分解可得

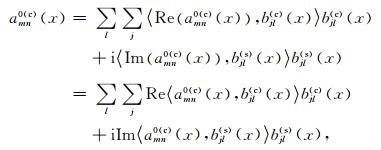
(15)

和

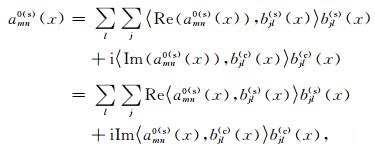
(16)

其中〈，〉表示内积，即〈u（x，z，ω），gmn（x）〉=∫u（x，z，ω）（gmn（x））*dx（“*”表示取复共轭）.Re（）和Im（）分别表示取实部和取虚部.

定义自由空间的传播算子如下

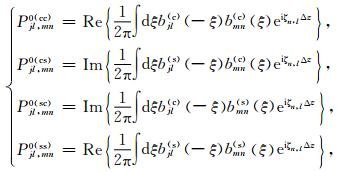
(17)

其中

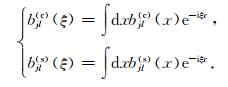
(18)

这里Pjl，mn0（cc），Pjl，mn0（cs），Pjl，mn0（sc）以及Pjl，mn0（ss）为在背景介质中的局部谐和基传播算子.从（17）式中可以看出它们表示了深度z处窗口位置为xn局部波数等于ξm的小波束到深度z+Δz处窗口位置为xl局部波数等于ξj的小波束之间的耦合.

深度z+Δz处的波场就可以通过将所有小波束的贡献叠加得到，即

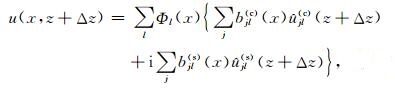
(19)

其中

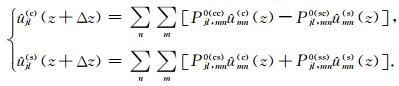
(20)

Φl（x）为（10）式中的相位扰动项，即

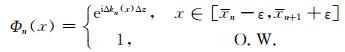
(21)

3.2.3 局部谐和基小波束背景传播算子

如果我们用统一的局部余弦/正弦基并且保持所有窗口的钟形窗函数形状相同，可以得到第n个窗口函数Bn（ξ）和位置为x=0的窗口函数B0（ξ）之间的关系

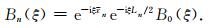
(22)

经过推导可以得到局部谐和基背景传播算子的最终表达式

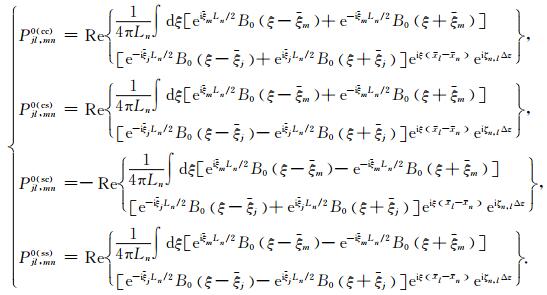
(23)

由于小波束很好的局部化特性，所以背景传播算子通常是稀疏矩阵，因此具有较高的效率.我们将在算例中讨论计算精度和效率，并与其他方法进行对比.

3.3 成像条件

这里我们利用传统的空间-频率域成像条件

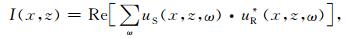
(24)

其中I（x，z）表示空间域的像，uS（x，z，ω）和uR（x，z，ω）分别表示源和接收器传播后的波场，“*”代表复共轭，Re（）表示取实部.

4 模型算例分析 4.1 二维横向变速模型中的点源脉冲响应

我们首先测试了局部谐和基传播算子在二维横向变速介质中的传播精度.我们测试的二维横向变速模型的大小与二维SEG/EAGE模型大小相同，在水平方向有1200个采样点，采样间隔为25 m，在深度方向有150个采样点，采样间隔同为25 m.背景速度为3000 m/s，横向速度变化梯度为10 m/s. 图 4给出了分别用局部余弦基传播算子和局部谐和基传播算子在该横向变速介质下计算出的点源脉冲响应.由于模型较为简单，从点源脉冲响应的相位上我们较难看出差别，但从图中可以明显看出用局部谐和基方法得到的波场噪声更少.

图 4 横向变速介质(v(x, z)=3000+10nx, m/s)中的点源脉冲响应 (a)用局部余弦基算子得到的在t=1 s时的响应; (b)用局部谐和基算子得到的在t=1 s时的响应. Fig. 4 Impulse response in model (v(x, z)=3000+10nx, m/s) (a) Snapshot at t=1 s by LCB method; (b) Snapshot at t=1 s by LHB method.
4.2 二维SEG/EAGE盐丘模型

二维SEG/EAGE模型在水平方向有1200个采样点，采样间隔为25 m，在深度方向有150个采样点，采样间隔同为25 m.最小的速度为1524 m/s，最大速度为4480 m/s，速度模型如图 5a所示.叠前数据共325炮，炮点间隔50 m，每炮的接收器为176个，间隔25 m，并且为左边单边接收.图 5b和图 5c分别为用局部余弦基方法和局部谐和基方法对二维SEG/EAGE盐丘模型叠前数据的偏移成像结果.从图中可以看到局部谐和基算子的成像质量在该模型上与局部余弦基的成像结果基本相同.

图 5 二维SEG/EAGE模型在叠前深度域偏移成像结果对比 (a)二维SEG/EAGE模型; (b)用局部余弦基方法得到的成像结果; (c)用局部谐和基方法得到的成像结果. Fig. 5 Prestack depth migration by the LCB and LHB beamlet migration using local harmonics (a)2D SEG/EAGE velocity model; (b) Image result of LCB method; (c) Image result of LHB method.
4.3 BP模型

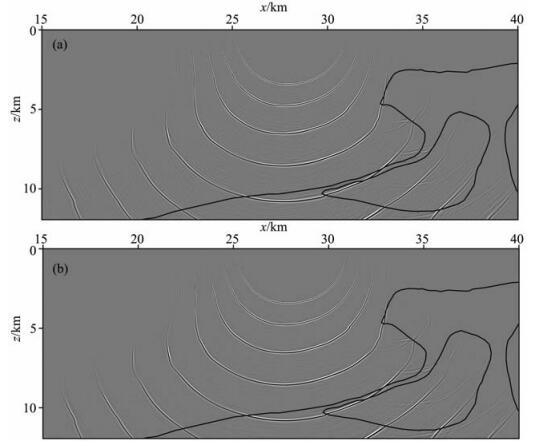
我们最后测试了较为复杂的二维BP模型.该模型在水平方向有5395个采样点，采样间隔为12.5 m，在深度方向有956个采样点，采样间隔同为12.5 m.最小的速度为1524 m/s，最大速度为4480 m/s，速度模型如图 7a所示.叠前数据共1348炮，炮点间隔25 m，每炮的接收器为1200个，间隔12.5 m，并且为左边单边接收.每道数据记录为14s，子波主频为27Hz.图 6给出了分别用局部余弦基算子和局部谐和基算子算出的BP模型中的点源脉冲响应.图 7b，图 7c和图 7d分别给出了用广义屏方法、局部余弦基方法和局部谐和基方法在叠前深度域所成的像，可以看出用局部谐和基方法所成的像（比如盐丘底部）有明显的改进.

图 7 二维BP模型叠前深度域偏移成像结果 (a)二维BP模型; (b)用广义屏方法得到的成像结果; (c)用局部余弦基方法得到的成像结果; (d)用局部谐和基方法得到的成像结果. Fig. 7 Prestack migration of BP 2D benchmark model (a) Velocity model; (b) Image result of GSP method; (c) Image result of LCB method; (d) Image result of LHB method.
图 6 BP模型中的点源脉冲响应 (a)用局部余弦基算子得到的在t=2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5 s时的响应; (b)用局部谐和基算子得到的在t=2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5 s时的响应. Fig. 6 Impulse response in BP model (a) Snapshot at t=2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5 s by LCB method; (b) Snapshot at t=2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5 s by LHB method.
4.4 计算精度和效率分析

局部余弦基小波束始终有两个对称的方向，在处理缓变介质时不存在精度问题.但是在处理有强速度反差的区域（如盐丘边界）时，每一个局部余弦基小波束都沿两个对称的方向沿拓，最后叠加起来会有一定的误差，并且这种误差是随着深度的增加累积的.而局部谐和基的传播算子不存在这种问题.由于二维SEG/EAGE盐丘模型相对简单并且深度较浅，因此局部谐和基的传播算子的优势并未得到体现.然而在较为复杂的BP模型中，由于盐丘形状较为复杂并且深度较深，因此我们看到深部盐丘边界的成像精度有较大差别.

我们来简单比较一下广义屏方法、局部余弦基方法和局部谐和基方法的计算效率.由于广义屏方法是全局（global）方法，因此计算效率较高，但是其成像精度低于另外两种方法.局部余弦基方法和局部谐和基方法都是利用了空间和波数域局部化特性的方法，主要包括波场分解、算子作用和波场重构三部分.这两种方法在波场分解和重构时由于都利用了快速余弦（正弦）变换，因此效率较高.然而在算子作用这一部分，由于传播算子是沿逐个窗对每个小波束进行作用的，所以较费时间.虽然局部余弦基和局部谐和基的传播算子形式不同，但是传播算子作用在复波场时需要的乘法运算次数是相同的，因此这一部分两种方法的计算效率也基本相同.总的来说，利用局部余弦基和局部谐和基的偏移成像方法效率基本相同，略低于广义屏方法.另外，小波束的偏移成像方法的效率还取决于一些参数的选取（如窗口长度、每一个小波束作用的窗口范围等）.在本文的算例中，小波束的方法需要的计算时间大约是广义屏方法的1.5倍.

5 结论与讨论

我们提出了一种利用局部谐和基进行复波场分解和传播的小波束域方法.这种方法与局部余弦基传播方法效率相同，但由于在传播算子上建立了方向性，因而传播精度上有了一定的提高，同时在传播过程中可以直接得到在局部角度域的方向信息.二维SEG/EAGE模型和BP模型的叠前偏移成像结果证明这种方法的有效性，通过与其他方法的比较可以看出该方法在偏移成像精度上的提高.我们将在后续工作中讨论如何将其运用到角度域内的振幅校正以及噪声衰减等.

致谢

感谢谢小碧、曹军、郑应才、陈文超在这项工作上的宝贵意见，感谢杨辉、何耀峰在程序编写上的帮助.感谢BP和Frederic Billette提供BP模型数据.

参考文献
[1] Gazdag J, Sguazzero P. Migration of seismic data by phase shift plus interpolation. Geophysics , 1984, 49: 124-131. DOI:10.1190/1.1441643
[2] Xie X B, Wu R S. Improve the wide angle accuracy of screen method under large contrast. SEG Technical Program Expanded Abstracts , 1998, 17: 1811-1814.
[3] de Hoop M V, Le Rousseau J H, Wu R S. Generalization of the phase-screen approximation for the scattering of acoustic waves. Wave Motion , 2000, 31: 43-70. DOI:10.1016/S0165-2125(99)00026-8
[4] Ristow D, Rühl T. Fourier finite-difference migration. Geophysics , 1994, 59: 1882-1893. DOI:10.1190/1.1443575
[5] Biondi B. Stable wide-angle Fourier finite-difference downward extrapolation of 3-D wavefields. Geophysics , 2002, 67: 872-882. DOI:10.1190/1.1484530
[6] Stoffa P L, Fokkema J T, Freire R M d L, et al. Split-step Fourier migration. Geophysics , 1990, 55: 410-421. DOI:10.1190/1.1442850
[7] Liu L, Zhang J. 3D wavefield extrapolation with optimum split-step Fourier method. Geophysics , 2006, 71: T95-T108. DOI:10.1190/1.2197493
[8] Chen L, Wu R S, Chen Y. Target-oriented beamlet migration based on Gabor-Daubechies frame decomposition. Geophysics , 2006, 71: S37-S52. DOI:10.1190/1.2187781
[9] 陈凌, 吴如山, 王伟君. 基于Gabor-Daubechies小波束叠前深度偏移的角度域共成像道集. 地球物理学报 , 2004, 47(5): 876–885. Chen L, Wu R S, Wang W J. Common angle image gathers obtained from Gabor-Daubechies beamlet prestack depth migration. Chinese J. Geophys. (in Chinese) , 2004, 47(5): 876-885.
[10] Wu R S, Wang Y Z, Luo M Q. Beamlet migration using local cosine basis. Geophysics , 2008, 73: 207-217. DOI:10.1190/1.2969776
[11] Wu R S, Mao J. Beamlet migration using local harmonic bases. 77th Annual Meeting, SEG, Expanded Abstracts , 2007: 2230-2234.
[12] Balian R. Un principle d'incertitude en theorie du signal ou en mecanique quantique. Comptes Rendus de l'Academie des Sciences, Paris, Serie Ⅱ , 1981, 292: 1357-1362.
[13] Coifman R R, Meyer Y. Remarques sur l'analyse de Fourier a fenetre. Comptes Rendus de l'Academie des Sciences:Paris, Serie Ⅰ , 1991, 312: 259-261.
[14] Mallat S. A Wavelet Tour of Signal Processing. (Second Edition). Academic Press, 1999 .
[15] Wickerhauser M V. Adapted Wavelet Analysis from Theory to Software. A K Peters, 1994
[16] Wu R S, Wang Y Z, Gao J H. Beamlet migration based on local perturbation theory. 70th Annual Meeting, SEG, Expanded Abstracts , 2000: 1008-1011.
[17] Margrave G F, Ferguson R J. Wavefield extrapolation by nonstationary phase shift. Geophysics , 1999, 64: 1067-1078. DOI:10.1190/1.1444614
[18] Margrave G F, Geiger H D, Al-Saleh S M, et al. Improving explicit seismic depth migration with a stabilizing Wiener filter and spatial resampling. Geophysics , 2006, 71: S111-S120. DOI:10.1190/1.2196034