2. 大庆钻探工程公司测井公司, 大庆 163412
2. Wireline Logging Company, Daqing Drilling Engineering Company, Daqing 163412, China
双侧向测井是一种应用极为广泛的电阻率测井仪器,由于其纵向分辨率较高、对地层电阻率变化敏感等特点,在储层评价中发挥着重要的作用.该仪器提供了两条探测深度不同的深浅侧向视电阻率曲线,根据这两个视电阻率的相对大小可以进行储层位置划分、油水层识别以及油气含量定量计算等.然而在薄储层情况下,受井眼泥浆、层厚以及围岩等诸多因素影响,深浅侧向视电阻率的相对大小通常不能准确反映实际储层的真实侵入特征,且视电阻率值与地层电阻率真值往往相差很大[1, 2].如何有效消除各种不利因素对双侧向测井响应的影响,从视电阻率中提取出地层电阻率真值和侵入带电阻率是当前薄储层解释评价中面临的一个难点问题.目前已经建立的一些不同的非线性反演算法[3~12]通常仅注重反演算法与合成数据上的简单验证,真正将双侧向反演技术直接应用于大量实际测井资料处理并取得较满意效果的报道仍然非常少.最近几年我们在与大庆油田的合作过程中,对不同区块上的双侧向测井资料进行了反演处理,在与试油结果对比后发现,影响实际双侧向测井资料反演效果的主要原因概括起来包括以下几个方面:一是强非线性.与感应测井相比[13],双侧向测井仪器对地层电导率变化的响应具有更强的非线性,初始模型对反演结果的影响往往较大.二是泥浆电阻率误差.由于目前使用的双侧向测井仪器没有配备泥浆电阻率的测量功能,只能根据地面上泥浆槽中的泥浆进行泥浆电阻率值估算,其误差对反演结果往往产生较大影响.三是多解性.从理论上说微球型聚焦测井(MSFL)可以提供侵入带电阻率信息,然而由于MSFL具有非常高的纵向分辨率,实际的测井资料显示MSFL曲线与DLL曲线很难匹配,特别是在高阻层,MSFL视电阻率普遍比DLL的高很多,无法从MSFL曲线提取出侵入带电阻率,只能用深浅侧向视电阻率曲线来同时确定地层原状电阻率、侵入带电阻率以及侵入半径等地层参数,这样将更容易引起多解性.四是解的不稳定性.双侧向测井资料反演是数学上典型的非线性不适定问题[14~16],例如在非侵入地层中如果假定地层原状电阻率与侵入带电阻率相等,则侵入半径无论取什么值都不会影响测井响应,这就导致解的不稳定.在过去,为了提高电测井资料反演结果的稳定性和降低多解性,人们主要采用奇异值截断[17, 18]或后验协方差矩阵[11, 12, 19, 20]等方法.这些方法在理论模型上往往可以取得较为满意的效果,但在进行实际资料处理时,由于同一油田不同区块、不同层段上的电阻率往往变化很大,导致测井响应的Fréchet导数矩阵与奇异值变化也很大,这些都将影响实际资料的处理效果.
为了提高双侧向测井资料反演结果的可靠性,本文对过去的有关算法进行了改进,提出了一种新的后验选取正则化因子的迭代反演方法.首先以水平层状地层中各个地层的原状电阻率、侵入带电阻率、侵入半径、层界面位置以及井眼泥浆电阻率作为模型向量,采用数值模式匹配算法快速计算出双侧向仪器的测井响应和Fréchet导数矩阵[11, 12];然后引入包含有电导率和侵入半径等导数的非二次函数作为稳定泛函,限制反演解的变化区域;最后通过Gauss-Newton法[21]给出逐步修改地层模型的迭代反演算法,在迭代过程中将Morozov偏差原理[22, 23]与Cholesky分解技术相结合,建立了一套后验选择正则化因子的方法,既保证了目标函数和测井响应拟合误差在迭代过程中同时不断下降,又实现了在极小化目标函数过程中输入资料与合成响应间的有效拟合,从而提高反演结果的稳定性和可靠性.通过对大庆油田三个不同区块(大庆油田西部区块、大庆油田朝长区块以及吉林油田徐升区块)56口井的134个试油层段进行反演处理,反演结果与试油结果相符合的共有114层,总符合率为114/134=85.07%,取得了满意的反演效果.
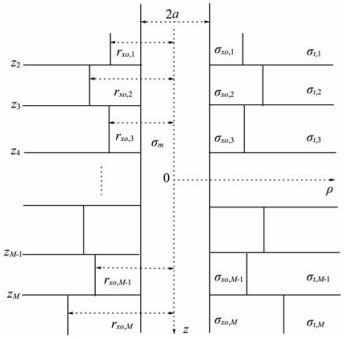
2 地层模型的参数化与迭代正则化反演图 1是层数为M的层状非均质地层模型,M维向量σt=(σt,1,σt,2,…,σt,M)、σxo=(σxo,1,σxo,2,…,σxo,M)和rxo=(rxo,1,rxo,2,…,rxo,M)分别表示地层原状电导率、侵入带电导率和侵入半径,M-1维向量z=(z2,z3,…,zM)表示地层界面位置,而井眼泥浆电导率则用σm表示.将这些参数结合在一起,构成一个4M维的模型向量:
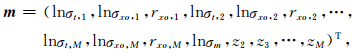
|
|
图 1 水平层状非均质地层模型图 Fig. 1 The model of a horizontally layered inhomogeneous formation |
其中T表示转置.为了后面的讨论简洁起见,所有的电导率参数均取为对数形式,并将模型向量所有可能的变化范围全体称为模型空间,用X表示.双侧向测井仪器是一种完全聚焦型的电测井仪器[1, 12],由9个环状电极分别镶嵌在圆柱形的绝缘棒上,通过特殊的聚焦条件在每个测量位置上同时测量出两个不同探测深度的视电阻率(深侧向RLLD和浅侧向RLLS).我们用2N维列向量dobs=(lnRa,1obs,lnRa,2obs,…,lnRa,2Nobs)T表示实测双侧向视电阻率(数据向量),所有m∈ X对应的理论响应d(m)构成了一个2N维的数据空间,用Y表示,显然d(m)是m的非线性函数.为了提高反演结果的稳定性,首先在模型空间X上引入如下稳定泛函:
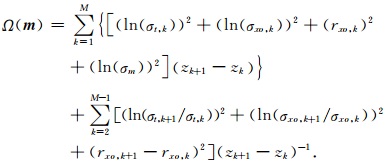
|
(1) |
(1)式实际上是连续函数空间中范数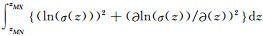
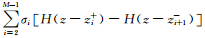
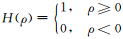
由Tikhonov正则化反演理论可知,双侧向测井资料反演就是要确定某个m* ∈ X,使得目标函数J(m)取极小值:
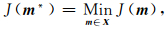
|
(2) |
其中J(m)=‖dobs-d(m)‖Y2 +αΩ(m),‖dobs-d(m)‖2=(dobs-d(m))T(dobs-d(m))是输入数据与理论合成数据的总方差,称作测井响应拟合误差,α为正则化因子.
如果正则化因子α已知,则对于一个给定的模型初值m(0),可用Gauss-Newtown法确定J(m)的极小值.设m(l)是第l次迭代的反演结果,将理论响应d(m)和稳定泛函Ω(m)在m(l)的微小邻域内进行Taylor展开,即
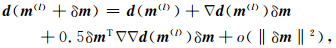
|
(3) |
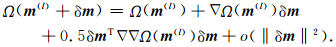
|
(4) |
再把(3)和(4)式代入目标函数J(m)中,仅保留到δm的二次项得

|
(5) |
其中Δy(l)=dobs-d(m(l))是输入数据与合成数据的残差,B(l)=▽d(m(l))是测井响应d(m)对模型参数m(l)的Fréchet导数矩阵(2N×4M阶),可由测井响应的Born近似表达式结合模式匹配半解析正演模拟技术快速求得[11, 12].而G(l)=▽Ω(m(l))和珡H(l)=0.5 ▽▽Ω(m(l))分别为稳定泛函的Fréchet导数列向量(4M阶)和Hessian矩阵(4M×4M阶),可对(1)式直接微分,计算其各元素的值.
进一步利用条件▽δmJ(m(l) +δm)=0,从方程(5)得模型参数的第l+1次校正量δm(l)满足下面的方程
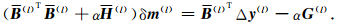
|
(6) |
直接求解上式得
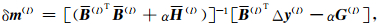
|
(7) |
进而新的模型参数可表示为
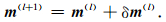
|
(8) |
重复进行方程(3)~(8)的运算直到满足收敛条件为止,可得双侧向反演问题的解m*.对于侧向测井来说,无论是理论模型还是实际资料处理,数值结果显示迭代10次即可满足收敛条件.
需要指出的是,Gauss-Newtown法的整个反演过程以及最后得到的反演结果均与正则化因子α有关.下面将基于Morozov偏差原理建立一套后验选取正则化因子的方法,在迭代过程中不仅使整个目标函数J(m)不断下降,还同时保证测井响应拟合误差‖dobs-d(m)‖Y2不断减少,实现输入资料与理论合成数据的最佳拟合.
3 正则化因子的选取首先分析Taylor展开式(4),稳定泛函(1)式在整个模型空间X上均满足Ω(m)>0,但(4)式右端的Hessian矩阵H(l)=0.5 ▽▽Ω(m(l))却不一定是正定的.当δm较大时,(4)式右端的二次展开式将破坏稳定泛函Ω(m)的非负性;而当层界面位置zk固定时,即在模型空间X的子空间Xl={m|m∈X,δzk=0,(k=2,3,…,M)}上,Hessian矩阵H(l)的子矩阵Hl(l)一定是正定的.另一方面,数值结果表明d(m)对层界面位置zk(k=2,3,…,M)的变化较为敏感,即向量B(l)中相对于δzk部分的元素往往较大[11].为了保证(5)式右端在整个求解空间上非负,也为了便于确定正则化因子α,我们忽略了Hessian矩阵H(l)中相对于δzk部分的所有分量,用子矩阵Hl(l)近似整个H(l)矩阵,这样方程(6)可近似地表示成
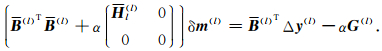
|
(9) |
由于子矩阵H1(l)是正定的,利用Cholesky分解结果Hl(l)=LL T,同时引入新向量
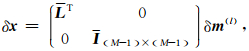
|
(10) |
代入方程(9)中,经过适当整理后得

|
(11) |
其中
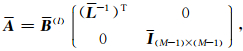
|

|
再利用奇异值分解结果A=1 Λ V T,代入(11)式得
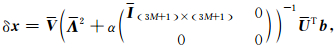
|
(12) |
将(12)式代入(10)式就可得到模型向量m的第l+1次校正量δm(l).
当数据误差水平已知时,采用Morozov偏差原理后验选择合适的正则化因子.将(5)式右端的第一项表示为
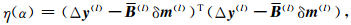
|
(13) |
可以证明η(α)是α的严格单调增函数,且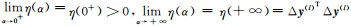
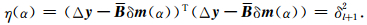
|
(14) |
在区间η[(0+),η(+∞)]上选取δl+12,使其满足η(0+)<δl+1 2<Δy (l)T Δy (l),则关于α的方程(14)的解是惟一存在的[16].由于(13)式是α的非线性函数,需要采用Newton迭代法确定(14)式的解:
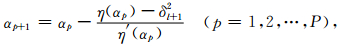
|
(15) |
其中η′(αp)是η(α)对α的导数,可以直接对(14)式求导得到

|
(16) |
再与方程(9)结合得
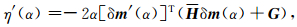
|
(17) |
其中δm′(α)可以通过对(11)式直接关于α求导得到
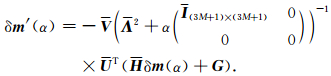
|
(18) |
在实际资料反演过程中,通常选取两个大小相差较大的正数αMN和αMX作为正则化因子的变化范围.每次迭代之前,先计算η(αMN)和η(αMX)的值,并用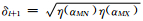
为了验证新的迭代正则化反演算法的有效性,利用该算法对理论模型和大庆油田的实际测井资料进行处理.
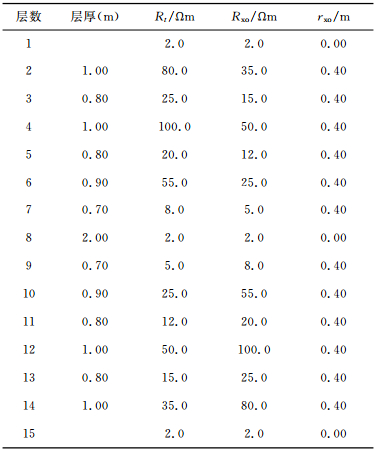
4.1 理论模型反演该模型由15层地层组成,模型参数见表 1,井眼半径和泥浆电阻率分别为0.1 m和2.0Ωm,采样间距为0.050 m,图 2给出了经半解析正演算法[2]合成的双侧向视电阻率曲线和真实的地层模型参数.从正演模拟结果看到,直接根据深浅侧向视电阻率的相对大小来判断地层的侵入特征将得到错误的结论.为了有效恢复地层的真实侵入特征并尽可能准确地确定地层电阻率真值,需要借助反演手段.
|
|
表 1 15层地层模型参数 Table 1 Model parameters of the 15-bed model |

|
图 2 正演合成的双侧向视电阻率曲线及地层模型参数 (a)侵人半径真值;(b)双侧向正演合成视电阻率曲线及地层电阻率真值. Fig. 2 Synthetic DLL logs and modll parameters (a) Invasion radius; (b) Synthetic DLL logs and formation resistivity. |
首先利用综合分层技术对合成的双侧向视电阻率曲线进行分层,确定地层原状电阻率、侵入带电阻率和层界面位置的初始值Rt,i(0),Rxo,i(0)和zi(0)(i=1,2,…,15),而侵入半径和泥浆电阻率的初始值rxo,i(0)和Rm(0)则统一取为0.5m和3.0Ωm.然后从初始模型开始对合成资料进行迭代正则化反演处理,确定模型参数真值.
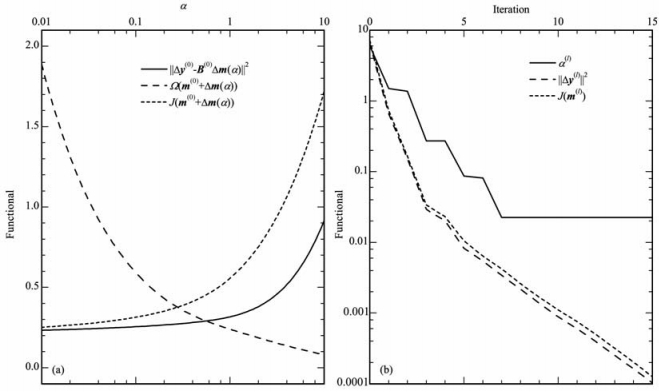
为考察正则化因子对反演结果的影响,对于给定的初始模型m(0),考察了初始迭代时不同正则化因子α对应的测井响应拟合误差‖Δy(0) -B(0) δm(α)‖Y2、稳定泛函Ω(m(0) +δm(α))以及目标函数J(m(0) + δm(α))的变化特征(见图 3a),这里Δy(0)=dobs -d(m(0)).图 3a显示:正则化因子α的增加将引起测井响应拟合误差‖Δy(0) -B(0) δm(α)‖Y2和目标函数J(m(0) +δm(α))的单调增加;当α<1时,稳定泛函Ω(m(0) +δm(α))对反演结果的影响较小,而当α>1时,稳定泛函Ω(m(0) +δm(α))对反演结果的影响明显增大,主要表现为测井响应拟合误差‖Δy (0) -B(0) δm(α)‖Y2明显增大.图 3b又给出了迭代正则化反演过程中正则化因子α(l)、测井响应拟合误差‖Δy(l) ‖Y2以及目标函数J(m(l))随迭代次数的变化情况,不难看出测井响应拟合误差‖Δy(l) ‖Y2和目标函数J(m(l))均是随迭代次数的增加逐渐减小.
|
图 3 初次迭代时α对反演结果的影响及迭代过程中α、测井响应误差和目标函数的变化 (a)初次迭代时不同α对反演结果的影响;(b)迭代过程中α、测井响应误差以及目标函数的变化. Fig. 3 The induence of regularization factor (initial iteration) and the change of regularization factors, log iitting errors and objective functions (iterative inversion) (a) The inluenceof a on inversionresults in initial iteration; (b) The change of regularization factors, log ti ting errors and objective functions during kerative mversion. |
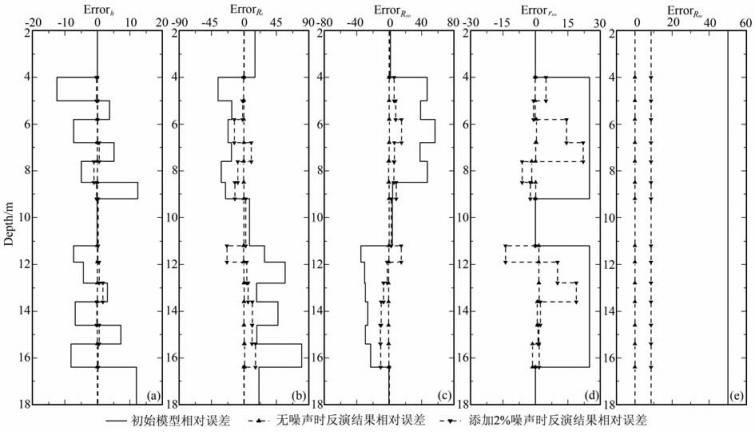
我们再来看一下反演结果:图 4b给出了经迭代正则化反演处理后得到的地层原状电阻率和侵入带电阻率(Rtiv和Rxoiv),与图 4a中真实地层模型的原状电阻率和侵入带电阻率(Rt和Rxo)进行对比看到,Rtiv和Rxoiv的相对大小与Rt和Rxo的相对大小完全一致,说明由新的迭代正则化反演得到的Rtiv和Rxoiv相对大小可以准确地判断出地层的真实侵入特征. 图 5则进一步给出了各模型参数的初始相对误差(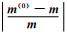
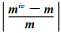

|
图 4 地层原状电阻率和侵人带电阻率的真值与反演结果 (a)模型的原状电阻率和侵人带电阻率;(b)无噪资料反演结果;(c)含2%噪声资料反演结果. Fig. 4 The true values and inversion results of modd (a) The true values of modll resistivity; (b) The nversion results from noiseless logs; (c) The nversion results from 2% noise log. |
|
图 5 各模型参数的初始相对误差与反演结果相对误差 (a)层界面位置相对误差;(b)原状电阻率相对误差;(c)侵人带电阻率相对误差;(d)侵人半径相对误差;(e)泥浆电阻率相对误差. Fig. 5 The relative errors of both initial modll and inversion results (a) The relative errors of the horizontal boundary depth; (b) The relative errors of the virgin formation resistivity; (c) The relative errors of the flushed zone resistivity; (d) TThe relative errors of the invasion radius; (e) TThe relative errors of the mud resistivity. |
进一步考察反演算法的抗噪能力,在测井记录上添加噪声.由nk=Ra,kεlogobs Wk确定添加到测井记录dobs上第k个元素的噪声,其中Wk从1和-1中随机抽取,εlog为噪声大小.取εlog=2%,得到一个含噪声的测井记录,然后再利用同样的初始模型进行迭代反演.图 4c给出了由含噪声的测井资料反演得到的地层原状电阻率和侵入带电阻率(Rtiv和Rxoiv),与图 4a对比看到,Rtiv和Rxoiv的相对大小与Rt和Rxo的相对大小仍保持一致,即Rtiv和Rxoiv的相对大小同样准确地显示出模型的真实侵入特征,表明反演算法具有较强的抗噪能力.图 5还给出了测井资料含有噪声时各模型参数的反演结果相对误差,与无噪声时相比,噪声的添加使得各模型参数的反演结果相对误差都增大,但仍都小于初始相对误差,反演结果表现出良好的稳定性.仔细观察图 5还可以看到:层界面位置的反演相对误差最小,而侵入半径的反演相对误差最大,这是由于侧向仪器对各模型参数的敏感程度不同造成的.在规范化的Fréchet导数矩阵中,视电阻率对层界面位置的导数最大,对侵入半径的导数最小[11],所以侵入半径的反演结果受噪声的影响较大.
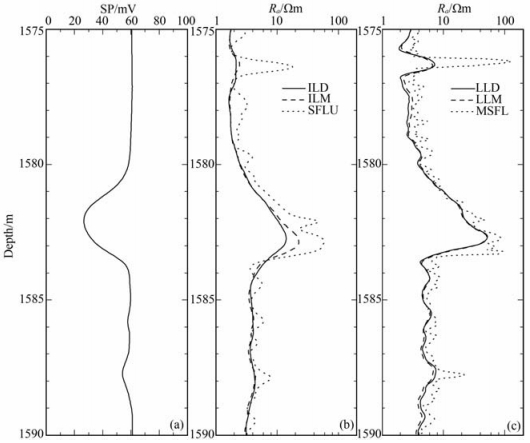
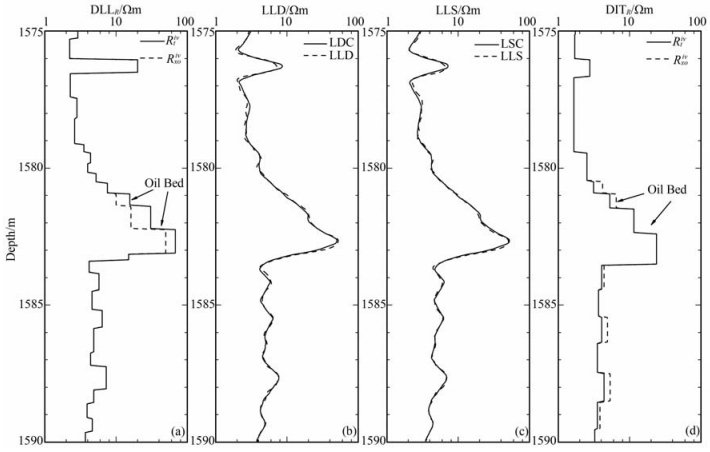
4.2 井场资料处理结果为了充分验证新反演算法的实效性,以便将反演方法作为薄储层中识别油气的重要研究工具,利用该反演技术对大庆油田三个不同区块56口井的测井资料进行处理.这些区块的很多含油储层属于砂泥岩薄交互层,其砂层厚度变化大、层数多、单层厚度薄、平面连续性差等特征给油水层的划分和识别带来极大的困难.为了有效反演井场实际资料,首先利用具有人机交互功能的综合分层软件对测井曲线进行分层,确定层界面位置和各个地层的电阻率初值,然后按照与理论模型完全相同的过程,从初始模型开始对侧向测井资料进行反演处理.由反演结果与试油结果的对比显示,反演结果的符合率为85.07%,取得了较为满意的效果.这里只给出其中一口井的处理结果,图 6是该井的测井记录曲线,其采样间距和井眼泥浆电阻率初值分别为0.0510 m和3.0Ωm.由图 6b和6c看到,该层段的双侧向和双感应视电阻率值都较大,具有明显的含油特征,但双侧向视电阻率显示该层段为无侵,双感应视电阻率显示为高侵(水层特征);由图 6a自然电位曲线显示,该层段的负异常幅度较大,地层具有较好的渗透性,压裂后可能产水;此外,利用中子、密度以及自然伽马曲线计算得到的该层段的有效孔隙度、泥质含量和含水饱和度分别为18.8%、16.1%和52%.综合分析这些结果后,解释人员认为该层段是油水层.由试油结果显示,在深度段1581.0~1583.4m之间是中产工业油层,解释结果与试油结论不一致. 图 7a给出了由双侧向测井资料反演得到的地层原状电阻率和侵入带电阻率,观察发现,在试油层段上反演得到的原状电阻率值明显比实测的视电阻率值高很多,且地层原状电阻率和侵入带电阻率的相对大小表现出非常明显的低侵特征,这与试油结论完全一致.此外,该反演结果在主频2.4G的笔记本上只耗时2min左右,速度较快,满足了生产应用对测井资料精细解释的要求.作为对比,图 7d给出了双感应测井资料的反演结果,显然在该层段上双感应测井资料的反演效果没有双侧向的明显.其原因是试油层段中存在低阻夹层(由MSFL曲线显示),在不到3m的试油层段上实际存在着4个不同电阻率的地层,其平均厚度不到1m.由于双感应仪器的纵向分辨率比双侧向的低很多,所以在厚度小于1 m的薄交互层上,双感应测井资料的反演效果比双侧向的差.图 7b和7c进一步给出了实测双侧向视电阻率与合成数据的对比,两条曲线均吻合得很好,再一次验证了反演算法的有效性和准确性.
|
图 6 大庆油田某井的测井记录 (a)自然电位测井记录;(b)双感应和球型聚焦测井记录;(c)双侧向和微球型聚焦测井记录. Fig. 6 Well logging data of Daqing Oil iield (a) SP:(b) DIT and SFLU:(c) DLL and MSFL. |
|
图 7 双侧向和双感应反演结果及双侧向视电阻率曲线拟合情况 (a)双侧向反演结果;(b)深侧向拟合情况;(c)浅侧向拟合情况;(d)双感应反演结果. Fig. 7 The DLL and DIT inversion results and misiit of the dual lateral logging (a) The invention results from DLL; (b) Misit of LLD; (c) Misit of LLS; (d) The invention results from DIT. |
本文研究建立了水平层状介质中双侧向测井资料的迭代正则化反演算法,能够同时反演地层原状电阻率、侵入带电阻率、侵入半径、层界面位置以及泥浆电阻率.在反演过程中,通过引入非二次稳定泛函和后验选择正则化因子,提高了反演结果的稳定性和可靠性.此外,将井眼泥浆电阻率也作为反演参数,降低了泥浆电阻率误差对反演结果的影响.理论模型与实际测井资料的反演结果证明,通过对双侧向测井资料的处理不仅能够有效提取出地层的侵入特征,而且反演得到的地层电阻率值与地层真值也更加接近,这对于正确识别油水层具有很大帮助.
| [1] | 张建华, 刘振华, 忤杰. 电法测井原理与应用. 西安: 西北大学出版社, 2002 . Zhang J H, Liu Z H, Wu J. The principle of electrical logging and its application (in Chinese). Xi'an: Northwest University Press, 2002 . |
| [2] | 汪宏年, 杨善德, 常明澈. 水平层状各向异性介质中侧向电阻率测井的快速数值模拟与应用. 测井技术 , 1998, 22(1): 22–31. Wang H N, Yang S D, Chang M C. Fast modeling of lateral resistivity logging in horizontal anisotropic layers and its application. Well Logging Technology (in Chinese) , 1998, 22(1): 22-31. |
| [3] | 张友生, 魏斌, 杨慧珠. 低阻油层双侧向测井的反演研究. 地球物理学进展 , 2003, 18(1): 85–89. Zhang Y S, Wei B, Yang H Z. A study on inverse of dual-lateral log in the low resistivity reservoir. Progress in Geophysics (in Chinese) , 2003, 18(1): 85-89. |
| [4] | 赵延文, 聂在平. 双侧向电阻率测井反演算法研究. 地球物理学报 , 1998, 41(3): 424–431. Zhao Y W, Nie Z P. An algorithm for the inversion of resistivity measurements from dual laterolog tool. Chinese J. Geophys. (in Chinese) , 1998, 41(3): 424-431. |
| [5] | 白东华, 陶辅周, 李小平, 等. 双侧向测井的数学反演. 四川大学学报 , 1992, 29(3): 352–359. Bai D H, Tao F Z, Li X P, et al. The mathematical inversion for the side way logging. Journal of Sichuan University Natural Science Edition (in Chinese) , 1992, 29(3): 352-359. |
| [6] | 汪宏年, 杨善德, 常明澈. 水平层状介质中侧向电阻率测井快速迭代反演与应用. 地球物理进展 , 1998, 13(4): 97–107. Wang H N, Yang S D, Chang M C. The fast nonlinear inversion of laterolog for the horizontal layers and its application. Progress in Geophysics (in Chinese) , 1998, 13(4): 97-107. |
| [7] | Yin H Z, Wang H M. Method for 2D Inversion of dual laterolog measurements. US Patent Application Publication, 2002 |
| [8] | Auken E, Christiansen A V. Layered and laterally constrained 2D inversion of resistivity data. Geophysics , 2004, 69(3): 752-761. DOI:10.1190/1.1759461 |
| [9] | 赵明, 高杰, 孙友国. 常规电测井联合反演研究与实际应用. 测井技术 , 2003, 27(1): 16–19. Zhao M, Gao J, Sun Y G. Joint inversion study of conventional electrical logging and its applications. Well Logging Technology (in Chinese) , 2003, 27(1): 16-19. |
| [10] | Mezzatesta A G, Eckard M H, Strack K M. Integrated 2-D interpretation of resistivity logging measurements by inversion methods. SPWLA 36th Ann. Log. Symp., 1995, Paper WW |
| [11] | Wang H N, Yang S D. A multiparameter iterative inversion of dual-laterolog in horizontally layered medium and its error analysis. IEEE Trans. On Geosci. and Remote Sensing , 2002, 40(2): 482-493. DOI:10.1109/36.992815 |
| [12] | 汪宏年, 陶宏根, 其木苏容, 等. 水平层状介质中双侧向资料的全参数正则化迭代反演与应用. 地球物理学报 , 2002, 45(Suppl.): 387–399. Wang H N, Tao H G, Qi Mu S R, et al. Regularized entire-parameter iterative inversion of dual-laterolog in horizontally stratified media an its application. Chinese J. Geophys. (in Chinese) , 2002, 45(Suppl.): 387-399. |
| [13] | 汪宏年, 陶宏根, 王桂萍, 等. 双感应测井资料的快速近似迭代反演. 地球物理学报 , 2007, 50(5): 1614–1622. Wang H N, Tao H G, Wang G P, et al. A fast approximate iterative inversion technique of dual induction logging data. Chinese J. Geophs. (in Chinese) , 2007, 50(5): 1614-1622. |
| [14] | 肖庭延, 于慎根, 王彦飞. 反问题的数值解法. 北京: 科学出版社, 2006 . Xiao T Y, Yu S G, Wang Y F. Numerical Methods for Inverse Problem (in Chinese). Beijing: Science Press, 2006 . |
| [15] | 王彦飞. 反演问题的计算方法及其应用. 北京: 高等教育出版社, 2007 . Wang Y F. Computational Methods for Inverse Problems and Their Applications (in Chinese). Beijing: Higher Education Press, 2007 . |
| [16] | Kirsch A. An introduction to the mathematical theory of inverse problem. New York: Springer Verlag, 1996 . |
| [17] | Xu P L. Truncated SVD methods for discrete linear ill-posed problems. Geophys. J. Int. , 1998, 135: 505-514. DOI:10.1046/j.1365-246X.1998.00652.x |
| [18] | Hansen P C. The truncated SVD as a method for regularization. BIT Numerical Mathematics , 1987, 27: 534-553. DOI:10.1007/BF01937276 |
| [19] | Scherzert O, Engl H W, Kunisch K. Optimal a posteriori parameter choice for Tikhnov regularization for solving nonlinear ill-posed problems. SIAM J. Numer. ANAL. , 1993, 30(6): 1796-1838. DOI:10.1137/0730091 |
| [20] | Kilmer M E, O'Leary D P. Choosing regularization parameters in iterative methods for ill-posed problems. SIAM J. Matrix Anal. Appl. , 2001, 22(4): 1204-1221. DOI:10.1137/S0895479899345960 |
| [21] | Kaltenbacher B. Some Newton-type methods for the regularization of nonlinear ill-posed problems. Inverse Problems , 1997, 13: 729-753. DOI:10.1088/0266-5611/13/3/012 |
| [22] | Scherzer O. The use of Morozov's discrepancy principle for Tikhonov regularization for solving non-linear ill-posed problems. SIAM J. Mumer. Anal. , 1993, 30(6): 1796-1838. DOI:10.1137/0730091 |
| [23] | Thomas B. Morozov's discrepancy principle and Tikhonov-type functionals. Inverse Problems , 2009, 25. DOI:10.1088/0266-5611/25/1/015015 |
| [24] | Routh P S, Oldenburg D W. Inversion of controlled source audio-frequency magnetotellurics data for a horizontally layered earth. Geophysics , 1999, 64(6): 1689-1697. DOI:10.1190/1.1444673 |
 2010, Vol. 53
2010, Vol. 53