2. 中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249
2. State Key Laboratory of Petroleum Resource and Prospecting, China University of Petroleum, Beijing 102249, China
垂直地震剖面(VSP)是一种井中地震观测技术.这种特殊的观测方式提供了独特的勘探信息,例如:采集井周围空间多波多分量的数据;提供子波、反褶积因子、速度等物理参数;研究井旁小构造成像及井附近地层的各向异性特征,对井孔周围储层进行精细研究;并可填补地面地震成像空白,与地面地震资料结合,增加反演的可靠性;可以为油田的开发和动态监测提供可靠的数据等.尤其是三维VSP技术更是受到了越来越多的重视.VSP数据处理解释中一个重要环节是数据的偏移成像.通常采用的Kirchhoff积分方法由于其固有的高频渐进假设和射线理论在复杂介质中的计算缺陷(如焦散和多路径等),使其在复杂构造区难以取得理想的成像效果,近年来,基于波动方程偏移成像方法取得了很大的发展[1],而叠前逆时深度偏移是获取复杂构造区成像最为精确的偏移技术.
逆时偏移不仅不受倾角限制(倾角可大于90°),能适用于任意复杂速度体,也能处理回转波、多路径等问题.它能够比较正确地计算波场振幅和偏移振幅,较其他偏移方法有明显的优势.该方法主要存在的应用瓶颈是:计算量大,存储量大,还有就是噪声问题.但近几年,随着高性能计算机和存储设备的发展,逆时偏移及其保幅偏移方法得到了迅速的发展.针对计算效率问题,本文采用空间无限阶精度的伪谱法实现了VSP逆时偏移,并讨论了张宇等提出的Laplacian滤波的噪声压制方法[2]在VSP逆时偏移中的应用.基于快速傅里叶变换的伪谱法不仅计算效率较高、便于实现[3~5],而且在空间方向没有数值频散误差.针对伪谱法边界效应的特殊性,本文采用Furumura提出的反周期扩展法[6, 7],可以完全消除来自于第一个周期的周期性边界波场干扰,边界吸收效果相对比较理想.
2 基于伪谱法的VSP逆时深度偏移VSP逆时深度偏移区别于地面逆时深度偏移之处在于检波器放置在井中,这点不同给VSP成像带来了一些特有的问题.共炮集的VSP逆时深度偏移同样需要求解两次波动方程,即一次正演波场,一次逆推波场;然后应用成像条件进行成像.对于炮点数较多的3DVSP逆时偏移一样存在计算效率问题.
本文采用伪谱法来实现VSP深度偏移,该方法具有实施简便、稳定性好等优点;其空间是无限阶,即不存在空间方向上的计算精度误差.首先给出二阶声波方程:
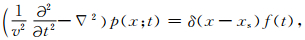
|
(1) |
其中,v是地下介质速度,f(t)是震源函数,p(x;t)是波场值.
应用伪谱法即先对空间x,z方向分别进行傅里叶变换,然后再逆变换,得

|
(2) |
其中,kx,kz分别是x和z方向的波数,F,F-1分别表示傅里叶正变换和逆变换.
为了提高计算精度,本文时间上采用了四阶差分公式[4]:
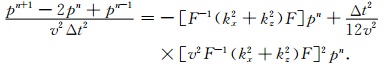
|
(3) |
利用式(3)可计算得到正演波场pF.
再通过(4)式利用上述相同求解方法,计算得到逆推波场值pB.最后利用相关成像条件(5)式进行成像[8, 9],所有单炮成像结果叠加,形成最终偏移成像结果.
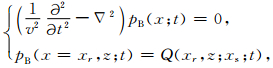
|
(4) |
其中Q是相应的炮点记录.
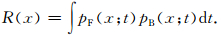
|
(5) |
张文生、张宇等人[10, 4]分别分析过二维和三维伪谱法的稳定条件,本文不再冗述.
3 反周期扩展法边界条件对于逆时偏移,在正演和逆推过程中都存在边界吸收问题.处理边界反射的方法已有较多的讨论. Cerjan等人在各向同性条件下提出了简单易行的指数吸收衰减型边界条件[11].但该方法主要问题是如何选取合适的吸收系数和扩充区域的网格数量,需要一定经验.若选取不合适,则会产生很强的边界反射.而且这种方法需在每个边界扩充较多的网格数,才能取得好的吸收效果.另一类边界条件是由Clayton等提出的基于旁轴近似的方法,该方法能较好地吸收垂直边界方向入射的波场,但随着入射角度增大,吸收效果也会明显变差[12~14].现在通用的方法是完全匹配层(PML),这种方法是由Berenger在处理电磁波传播中的边界问题提出的,后来被引入到弹性介质中[15].但该方法在计算区和边界需要计算不同的方程,针对这个问题,Wang等人提出了非分裂的完全匹配层方法[16, 17],但该方法在实施上相对复杂.而本文主要是为了消除伪谱法的边界效应,由于伪谱法实施过程中要对空间变量进行傅里叶变换,这就必然会导致波场在空间域周期性的延拓,这也是伪谱法特殊的边界效应,其区别于其他有限差分方法的边界问题,本文采用了Furumura提出的反周期扩展法(Antiperiodic Extension)来消除这种边界效应[6, 7].
为了说明伪谱法的边界问题,首先给出了一个v=2500m/s常速模型(图 1),震源设在x=500m,z=500m的位置处.由于伪谱法分别在x,z方向进行傅里叶变换(以二维为例),所以致使震源周期性地在左、右和上、下出现虚震源(图 2a中白色震源所示).导致的结果就是周期性地由虚震源传回假波场(或称为伪波场).从记录t=0.5s时刻波场快照(图 2b)可明显看见首先从右侧、底部及右下角点处由虚震源传播回来的伪波场.随着记录时间的增长将会从上部、左侧及其他三个角点传播回伪波场,这就造成了有效波和来自不同方向周期性的伪波场发生混叠.所以对于伪谱法必须处理好边界问题,否则有效波场会受到严重干扰.为了消除这种周期性问题,本文采用了Furumura的反周期扩展法.该方法的基本思想就是在按照一定时间步长递推过程中,把虚震源产生的周期性假波场剔除出去.具体实施过程为:第一步由长度为N的f(nΔx)的函数,计算出含有周期性波场的pper;第二步是扩展f(nΔx)为2N长度的新函数,计算出反周期波场panti;第三步在pper中减去panti就得到了最终的有效波场.这个过程可类似地应用于消除来自不同方向的伪波场.虽然这种方法在一定程度上增加了计算量,但该方法不需要扩边处理,而且对于消除伪谱法所带来的周期性波场的效果是比较好的.
|
图 1 常速度模型 Fig. 1 A constant velocity model |

|
图 2 伪谱法产生的边界问题 (a)伪谱法产生的周期性虚震源示意图,其中黑色为真震源,白色为虚震源;(b)为(a)在0.5 s时刻的波场快照;(c)采用反周期扩展法消除垂直方向虚震源示意图;(d)为(c)在0.5 s时刻的波场快照;(e)采用反周期扩展法消除水平方向虚震源示意图;(f)为(e)在0.5 s时刻的波场快照;(g)采用反周期扩展法消除两个方向虚震源示意图;(h)为(g)在0.5 s时刻的波场快照. Fig. 2 Boundary condition of pseudo-spectral method (a) Periodic shots caused by using the traditional Fourier differentiation scheme; (b) Snapshot of Fig. 2a displayed at t=0.5 s; (c) Vertical periodic shots were eliminated using the antiperiodic extension method; (d) Snapshot of Fig. 2c at t=0.5 s; (e) Horizontal periodic shots were eliminated using the antiperiodic extension method; (d) Snapshot of Fig. 2e at t=0.5 s; (g) All periodic shots were eliminated using the antiperiodic extension method; (h) Snapshot of Fig. 2g at t=0.5 s. |
为了计算得到反周期波场,需要扩展长度为N的函数f(nΔx)为(6)式,其长度增加为2N:
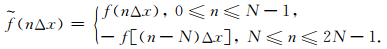
|
(6) |
然后,对(6)式进行傅里叶变换得:

|
(7) |
则波场空间二阶导数的计算可将(7)式乘-kxkx后做反傅里叶变换得出:
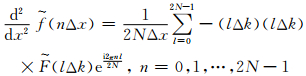
|
(8) |
通过(8)式求出的波场取其前N个点即为所要输出的反周期波场panti,后N个点没被用到.
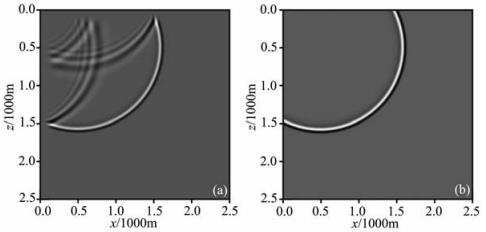
为了验证该方法的有效性,对上述常速度模型(图 1)进行处理,并与指数衰减型的边界条件进行了对比.首先利用反周期扩展法消除垂直方向虚震源(图 2c),图 2d为t=0.5s的波场快照,可见此时仅有水平方向的假象;同理,图 2e为消除了水平方向虚震源的示意图,图 2f为t=0.5s的波场快照,此时仅有来自垂直方向的假象;最后,同时消除垂直和水平方向的虚震源(图 2g),此时仅剩下了真震源,则在t=0.5s的波场快照上,就不会存在由于周期性虚震源引起的波场假象.图 3对比了利用指数衰减型(图 3a)和反周期扩展法(图 3b)的边界条件.明显看出,后者消除了这种周期性震源引起的边界效应,值得注意的是此时仅仅消除了来自第一个周期的伪波场,随着时间的推移还会有第二周期、第四周期等的伪波场.但对于我们所研究的问题,一般消除来自第一周期伪波场的影响就足够了.针对不同的问题,还可以把反周期扩展法和指数衰减型的边界条件结合使用,比如在x方向采用指数衰减型的边界条件,而在z方向采用反周期扩展法.这样既可保证能比较好地消除边界反射,同时又不会增加太多的计算量.
|
图 3 两种边界条件效果对比图 (a)指数衰减型的边界条件;(b)反周期扩展法边界条件. Fig. 3 Comparison of two kinds of boundary conditions (a) Absorbing boundary condition; (b) Antiperiodic extension method. |
我们首先计算了VSP逆时深度偏移的响应脉冲.对于2D VSP偏移而言,在常速度介质中,偏移响应脉冲是一个分别以炮点和检波点为焦点的椭圆;而对于3D VSP而言是一个椭球体.下面分别以点脉冲和30Hz的雷克子波为输入(图 4a为点脉冲和图 4c为雷克子波),分别经过逆时偏移就得到了相应的偏移脉冲响应.如图 4b为点脉冲的偏移响应,图 4d为雷克子波的偏移响应,其中白色竖线为井所在位置.可见二者的偏移脉冲响应的形状都是标准的椭圆,验证了偏移算法的正确性.

|
图 4 (a)点脉冲;(b)脉冲(a)的VSP逆时偏移响应;(c)30Hz的雷克子波;(d)雷克子波(c)的VSP逆时偏移响应 Fig. 4 (a) Apulsefunction; (b) VSP RTM impulse response to a pulse function; (c) 30 Hz Ricker wavelet; (d) VSP RTM impulse response to Ricker wavelet |
为了分析2D VSP逆时深度偏移的有效性及存在的噪声问题,本文设计了三个模型:其一是绕射点模型;另一个是地堑模型;还有一个半圆隆起模型.采用Zhang等人提出的Laplacian滤波方法来压制逆时偏移噪声[2].该方法主要原理是消除逆时偏移过程中由于较大入射角产生的噪声,Laplacian滤波就相当于进行有限角度的滤波.为了保证滤波前后振幅不变,首先要对输入信号在频率域进行滤波,再进行逆时偏移,然后进行Laplacian滤波,最后乘以速度v2(具体流程可参见文献[2]).
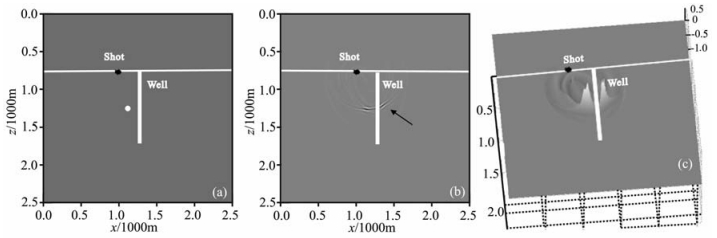
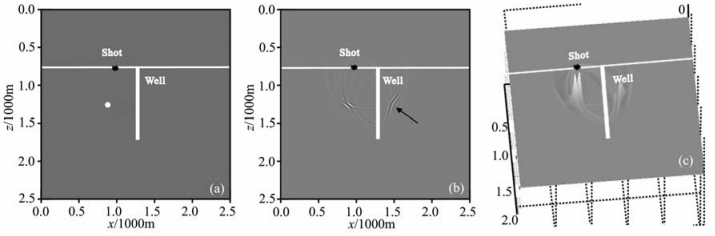
5.1 绕射点模型首先设计了含有一个绕射点的模型(图 5a),模型大小为256×256,网格间距为10m,炮点xz坐标为(1060m,820 m),井位置为x=1200 m,绕射点位置xz坐标为(1160 m,1310 m).用本文介绍的2DVSP逆时偏移方法进行成像,结果见图 5b,可以发现绕射点已经很好归位,但同时在井的另一侧也出现了一个能量聚焦点--假象(图 5b中黑色箭头所指位置),这是由于VSP特殊观测方式在地下覆盖次数不足造成的,在图 5c中显示出了成像点处的振幅.又设计了另一个模型(图 6a)加大了绕射点与井的距离,绕射点xz坐标(960m,1310m),逆时偏移结果如图 6b,可见在井的另一侧同样出现了假象点(图 6b中黑色箭头所指示位置),可以通过增加覆盖次数对其消除.所以对于VSP偏移成像,若覆盖次数不足在近井区更易产生假象问题.
|
图 5 (a)近井绕射点模型示意图;(b)单炮VSP逆时偏移结果;(c)振幅大小对比图 Fig. 5 (a) The model of a diffraction point near the well; (b) A single shot VSP RTM image; (c) Migrated amplitude map |
|
图 6 (a)远井绕射点模型示意图;(b)单炮VSP逆时偏移结果;(c)振幅大小对比图 Fig. 6 (a) The model of a diffraction point far away from well; (b) A single shot VSP RTM image; (c) Migrated amplitude map |
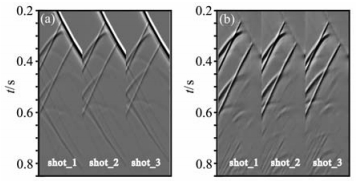
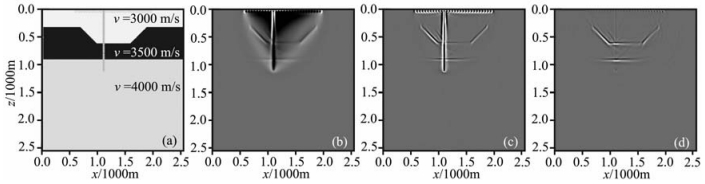
本文设计了一个地堑模型,网格大小为256× 256,网格间距为10 m,炮点和井xz坐标分别为(600m,30m)和1100m,如图 8a灰色圈所示.共激发了28炮,间距为50 m,每炮108道接收,道间距为10m.图 7a抽取出了3炮VSP记录,图 7b是从图 7a中分离出的上行波.首先利用未做波场分离处理的28炮VSP记录进行偏移成像,结果如图 8b.可见图 8b中存在较严重的偏移噪声问题,应用上述Laplacian滤波噪声压制方法处理后的结果如图 8c.与图 8b相比偏移噪声明显得到压制,所以该噪声压制方法对VSP逆时偏移是比较有效的.从图 8b、8c中不难发现不仅地下地层能成像,而且炮点和检波点位置也分别成像,这主要是直达波场成像的结果.
|
图 7 (a)地堑模型中抽取的三炮VSP记录;(b)为分离出来的上行波场 Fig. 7 (a) Three VSP shot records; (b) The separated upgoing wavefield of (a) |
|
图 8 (a)地堑速度模型;(b) VSP全波场逆时偏移结果;(c)为图 8b经过Lapktrn滤波后结果;(d)分离出的上行VSP波场逆时偏移结果 Fig. 8 (a) Velocity of graben model; (b) RTM image using the full wavefield; (c) The image with Laplacian filter applied to (b); (d) The RTM image using the separated upgoing wavefield only |
下面又利用从28炮VSP记录中分离出的上行波场进行偏移成像(即分离出去了下行波和直达波,如图 7b),结果为图 8d.与图 8c比较在炮点和检波点位置处没有成像噪声,主要原因是分离出去了直达波.可见对于VSP逆时偏移,当切除直达波后,再通过Laplacian滤波是可以较好地达到压制噪声效果的.
5.3 半圆隆起模型下面设计了中间含有一个半圆隆起的四层模型(图 9a),网格大小为512×300,间距为10 m,中间黑色竖线为井所在位置即x=2560m.共激发了90炮,第一炮xz坐标为(790m,750m),炮间距为40m,每炮153道接收,道间距为10 m.图 9b为利用90炮未做波场分离的VSP记录进行逆时偏移的结果,可见井旁构造都能正确成像.由于未对VSP记录进行波场分离处理,所以在最终VSP逆时偏移结果中,直达波在检波点和炮点位置成像,如图 9b中的竖线.而且由于逆时偏移可对所有波动现象进行成像(包括直达波、下行波及上行波等),所以成像孔径大于基于单次绕射的成像方法.
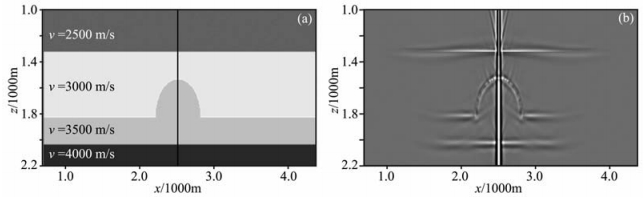
|
图 9 (a)半球隆起速度模型;(b) VSP全波场逆时偏移结果 Fig. 9 (a) Velocity model; (b) RTM image using full wavefield |
最后对某地区VSP野外采集的数据进行了逆时偏移成像.该工区成像目的层是埋藏深度在4000~5800m的井周围岩溶体系和底砾岩.根据该区地面地震偏移剖面,可发现在深度5600 m左右有明显的溶洞响应(图 10中白色箭头所示),并经过该区钻井资料证实了溶洞的存在.本文选取该工区3D VSP过井炮线进行了逆时偏移成像(图 10a)及深度域Kirchhoff VSP偏移成像(图 10b).井位于x=5000m处,炮间距为100m,共有98炮在井两旁对称分布;采用间距为20m的32个检波器接收,下放深度从3000~3620m.并与地面地震3D Kirchhoff法叠前时间偏移结果(图 10c)进行了比较,两种方法采用相同的速度模型和输入资料,VSP Kirchhoff法偏移孔径为5000m.可见三者主要层位对应性比较好,在偏移剖面中都存在明显的溶洞特征.从图 10中不难看出,VSP偏移成像分辨率高于地面地震的,而且逆时偏移在近井区成像连续性上明显优于基于高频射线理论的Kirchhoff法VSP偏移结果.验证了VSP逆时偏移在成像上具有一定的优势.

|
图 10 VSP逆时偏移结果(a)、深度域Khxhhoff法VSP偏移结果(b)和该区地面地震偏移结果(c) Fig. 10 The migration image from VSP RTM (a), Kirchhoff VSP (b), and surface seismic data (c) |
本文主要研究了基于伪谱法的VSP逆时深度偏移,逆时偏移是能对地下复杂构造精确成像的一种偏移方法.近几年随着计算能力和存储能力极大增强,该方法也渐渐被引入工业界.本文采用了简便易行、效率较高的伪谱法实现了二维VSP逆时深度偏移,并应用反周期扩展法较好地消除了伪谱法特殊的周期性边界效应.虽然针对处理伪谱法边界效应的反周期扩展法在一定程度上增加了计算量,但可结合其他的方法同时使用(比如指数衰减型的边界条件),即针对某些方向上的边界运用反周期扩展法,在其余方向应用指数衰减型的边界条件,这样既可能达到较好处理边界效应问题,又能在一定程度上减少计算量.本文通过对VSP绕射点模型的逆时偏移成像结果进行对比分析,讨论了该偏移方法在近井区对称位置易产生偏移假象问题.对地堑模型和半圆状模型进行了偏移成像,并经过Laplacian滤波压制噪声处理后,都获得了较好的成像效果.而且也针对VSP的全波场记录和分离出的上行波场分别进行了逆时偏移成像,通过对比分析,明显发现直达波在炮点和检波点处成像.利用张宇等人提出的Laplacian滤波方法也能有效地压制VSP逆时偏移成像噪声.最后,对某地区VSP实际资料进行了逆时偏移成像,并与Kirchhoff法VSP偏移及该区地面地震偏移剖面进行了对比,显示出VSP逆时偏移在近井区成像上具有明显的优势.
致谢感谢中石油各理事单位对课题研究的资助和支持;感谢塔里木油田公司提供的地面地震资料.特别感谢CGGVeritas公司张宇博士对本研究提供了大量帮助和建设性意见.感谢中国石油大学(北京)地质地球物理综合研究中心提供的良好科研环境.感谢中国石油大学(北京)地质地球物理综合研究中心白英哲、马志霞和白海军等人提供的帮助.
| [1] | 陈生昌. 三维VSP数据的波动方程偏移成像. 天然气工业 , 2008, 28(3): 51–53. Chen S C. Wave equation migration for 3-D VSP data. Natural Gas Industry (in Chinese) , 2008, 28(3): 51-53. |
| [2] | Zhang Y, Sun J. Practical issues in reverse time migration:true amplitude gathers, noise removal and harmonic source encoding. First Break , 2009, 27: 53-59. |
| [3] | Gazdag J. Modeling of the acoustic wave equation with transform methods. Geophysics , 1981, 46: 853-859. |
| [4] | Zhang Y, Sun J, Gray S. Reverse-time migration:amplitude and implementation issues. Expanded Abstracts of 77th SEG Mtg , 2007a: 2145-2148. |
| [5] | Kosloff D, Baysal E. Forward modeling by a Fourier method. Geophysics , 1982, 47: 1402-1412. DOI:10.1190/1.1441288 |
| [6] | Furumura T, Takenaka H. A wraparound elimination technique for the pseudospectral wave synthesis using an antiperiodic extension of the wavefield. Geophysics , 1995, 60: 302-307. DOI:10.1190/1.1443760 |
| [7] | Furumura T, Kennett B, Takenaka H. Parallel 3-D pseudospectral simulation of seismic wave propagation. Geophysics , 1998, 63: 279-288. DOI:10.1190/1.1444322 |
| [8] | Haney M. Insight into the output of reverse-time migration:what do the amplitudes means. Expanded Abstracts of 75th SEG Mtg , 2005: 1950-1953. |
| [9] | Chattopadhyay S, McMechan G. Imaging conditions for prestack reverse-time migration. Geophysics , 2008, 73: S81-S89. DOI:10.1190/1.2903822 |
| [10] | 张文生, 何樵登. 二维横向各向同性介质的伪谱法正演模拟. 石油地球物理勘探 , 1998, 33(3): 310–319. Zhang W S, He Q D. Pseudospectral modeling of 2-D transversely isotropic media. Oil Geophysical Prospecting (in Chinese) , 1998, 33(3): 310-319. |
| [11] | Cerjan C, Kosloff D, Kosloff R, et al. A nonreflection boundary condition for discrete acoustic and elastic wave equations. Geophysics , 1985, 50: 705-708. DOI:10.1190/1.1441945 |
| [12] | Clayton R, Engquist B. Absorbing boundary conditions for acoustic and elastic wave equations. Bull. Seism. Soc. Am. , 1977, 67: 1529-1540. |
| [13] | Cao S, Greenhalgh S. Attenuating boundary conditions for numerical modeling of acoustic wave propagation. Geophysics , 1998, 63: 231-243. DOI:10.1190/1.1444317 |
| [14] | Kosloff R, Kosloff D. Absorbing boundaries for wave propagation problems. J. Comp. Phys. , 1986, 63: 363-376. DOI:10.1016/0021-9991(86)90199-3 |
| [15] | Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves. J.Comp. Phys. , 1994, 114: 185-200. DOI:10.1006/jcph.1994.1159 |
| [16] | Wang T, Tang X. A nonsplitting PML for the FDTD simulation of acoustic wave propagation. Expanded Abstracts of 71th SEG Mtg , 2001: 345-348. |
| [17] | Wang T, Tang X. Finite-difference modeling of elastic wave propagation:a nonsplitting perfectly matched layer approach. Geophysics , 2003, 68: 1749-1755. DOI:10.1190/1.1620648 |
 2010, Vol. 53
2010, Vol. 53

