2. 昆明工业职业技术学院, 昆明 650302
2. Kunming Vocational and Technical College of Industry, Kunming 650302, China
声波在地球介质中的传播实际上是一个波动方程的正演过程, 为了获取地球内部信息, 正演模拟技术一直是地球物理学中非常重要的研究内容.优良的正演数值方法能够大大提高波场模拟的效率.20世纪以来, 计算地球科学领域陆续出现了多种数值模拟方法, 如有限差分法[1~3]、伪谱法[4]、有限元法[5]、射线追踪法[6]等, 这些方法都有各自的优点和不足, 这在Yang [7]的研究中已指出.
有限差分法因为其编程易实现、相同网格点数情况下存储量小和计算迅速、并行效率高等优点在地球物理学中得到广泛应用.但使用传统的显式差分格式进行波动方程求解时, 会因为数值波速与真实波速的不同步, 在粗网格情况下产生假波, 引起严重的数值频散[2, 8~11], 使得人们难以辨别真假波, 失去了正演模拟计算的意义.为消除数值频散, 通常采用的方法有两种, 一是构造高阶数值格式[2], 二是加细网格.高阶数值格式虽具有高阶精度, 但并不相应具有低数值频散[8]; 若采用加细网格来消除频散, 则会带来存储量的急剧增加; 另一方面, 网格点数的增多, 必将导致计算时间的大量增加, 并且由于空间步长减小而不得不缩短时间步长(因为受显式方法稳定性条件的限制), 从而进一步导致迭代步数增多, 计算耗时剧增, 因此对于大尺度波场模拟计算, 这种加密网格的做法是不现实的.
为了克服有限差分方法存在的数值频散问题, 以适应大尺度波场模拟的要求, Yang [9]在2003年率先将一种近似解析离散化算子[12]引入波动方程的数值求解中.该算子是基于截断的泰勒展式以构造空间局部插值函数, 并通过相邻网格点之间的连接关系, 用位移及其梯度的线性组合来逼近空间高阶偏导数.在使用该离散算子的同时, 结合不同的时间离散方法, 可以获得具有低数值频散的数值格式.目前已经发展了NADM[9]、ONADM[13]、INADM[14]、WNADM[15]等基于泰勒公式展开进行时间离散的数值方法, 以及同时使用了三阶Runge-Kutta和算子级数方法的IRK-DSM方法[16], 这些方法均具有良好的压制数值频散的效果.但这些方法均为非辛格式.
我们知道, 地震波在地球介质中的传播, 理论上是一个保守无耗散的过程, 是一个单参数连续辛变换[17].波动方程可以表述为哈密尔顿系统的形式, 且其时间上具有辛结构.冯康[18]认为, 对于哈密尔顿系统的离散格式应当采用保辛的数值格式.他和他的研究小组, 从哈密尔顿力学的数学基础---辛几何出发, 给出了完整的单辛算法理论框架.辛算法能够严格保持哈密尔顿系统的辛结构, 而且具有计算的稳健性、长时间跟踪能力[19, 20].
根据哈密尔顿函数的形式, 波动方程可以转化为线性可分哈密尔顿系统.一类有效的针对可分哈密尔顿系统的辛格式为保辛的分部龙格库塔格式(partitioned Runge-Kutta), 简称辛PRK格式[18, 21].孙耿[21]在1997年的研究中指出, 可分哈密尔顿系统的低阶显式辛格式中, 二阶显式的辛PRK Lobatto ⅢA-ⅢB方法无论从工作量还是稳定性上与其他辛PRK格式比较, 均为最优.针对波动方程的哈密尔顿形式构造单辛算法的传统做法是:在时间上使用辛差分离散, 空间上采用二阶或者四阶精度的差分格式进行离散[21].但应该指出的是, 采用传统的空间离散方法, 即目前已有的求解波动方程的辛方法不能很好地压制数值频散, 因此, 我们希望寻找一种合适的空间离散方法, 使得辛格式在保辛的同时, 能有效压制数值频散.
本文基于声波方程的哈密尔顿表述, 在时间上采用二阶显式的辛PRK LobattoⅢ A-ⅢB格式[21], 空间上采用近似解析的离散方法[7, 9, 13~15], 得到了一种时间精度为二阶, 空间精度为四阶的新型辛格式.稳定性分析、数值频散分析, 以及波场模拟结果表明, 这种新的辛方法具有有效压制数值频散、计算快速以及低存储需求等优良性质.
2 NSPRK方法的构造 2.1 二阶辛PRK方法首先回顾可分哈密尔顿系统的二阶显式辛PRK格式的构造过程.一般的2n维哈密尔顿系统可以写成如下形式[18, 21]:

|
(1) |
其中, 满足下列条件的系统称为可分的哈密尔顿系统:
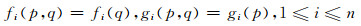
|
(2) |
下面以一维波动方程:
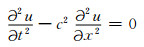
|
(3) |
为例, 说明其哈密尔顿系统和二阶辛PRK格式.
若令v=∂u/∂t, 则可将方程(3)写成如下线性可分的哈密尔顿系统:
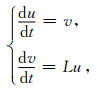
|
(4) |
其中, 偏微分算子L=c2
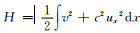
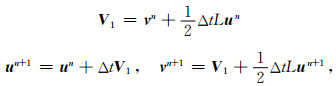
|
(5) |
其中un、vn分别代表第n时间层的离散位移向量以及粒子速度向量.依据PRK方法保辛的判别方法[18, 21], 容易证明该计算格式具有保辛的性质.
2.2 空间离散
在辛格式构造中, 通常采用二阶或者四阶差商[21]来逼近算子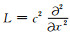
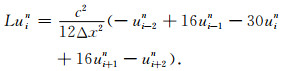
|
(6) |
本文拟采用近似解析离散化的思想来离散方程(4)中的空间导数.为此, 令:
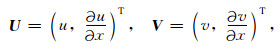
|
(7) |
则方程(4)可变为
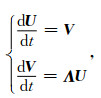
|
(8) |
其中, 算子矩阵定义为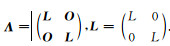
针对哈密尔顿系统(8), 本文采用近似解析离散方法离散方程(8)中的高阶空间导数.对于一维情况, 有如下计算公式[13]:

|
(9a) |
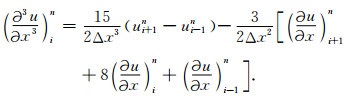
|
(9b) |
对于粒子速度v, 我们采用类似(9a)、(9b)的公式逼近.换言之, 将公式(9a)和(9b)中的u用v代替即可得到计算v高阶空间导数的近似公式.对于二维情形, 其高阶空间导数的计算参见附录.为叙述方便, 将本文的近似解析(Nearlyanalytic)辛PRK格式, 简称为NSPRK格式, 而空间离散若采用前述传统空间离散格式(6)所得的辛PRK方法, 简称为SPRK方法.由于NSPRK方法在时间上采用了辛格式, 因此它在时间上具有保辛性, 另一方面, 由于NSPRK在空间上采用了近似解析离散方法, 因此NSPRK方法具有时间保辛和弱数值频散的双重优势.在后面, 我们将通过数值实验证实这一优点.
3 稳定性条件稳定性分析是显式差分方法的重要研究内容, 因此本节将分析并给出NSPRK方法的稳定性条件.为此, 我们首先定义库朗数C如下:
一维情形: C=c0Δt/Δx
二维情形, 若令Δx=Δz=h, 则: C=c0Δt/h
c0为波速, Δx与Δz分别为x和z方向的步长.
类似于Yang等人[13]的稳定性分析方法, 我们可得NSPRK方法的稳定性条件如下:
对于一维情况:
对于二维情况: 
求解波动方程的有限差分方法都是用离散形式的差分方程逼近连续形式的微分方程, 因此, 会造成数值波速与真实波速的不同, 从而导致离散方法存在数值频散或称为频散误差.为研究这种频散误差, 我们首先定义数值波速与真实波速的比率R如下:

|
(10) |
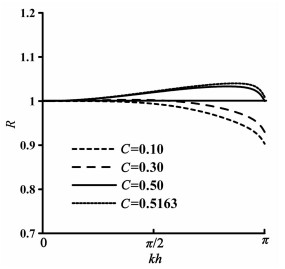
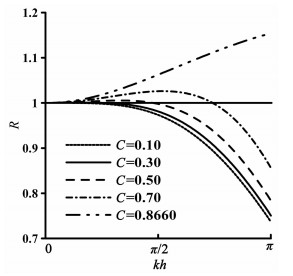
其中cnum表示数值波速, 而c0为真实波速.显然, R越接近1, 表示数值波速与真实波速的误差越小, 即数值频散越小, 反之, 表明数值频散越严重.采用Dablain[2]和Yang [13]的数值频散分析方法, 可以得到NSPRK方法和SPRK方法在不同库朗数下的数值频散关系, 如图 1和图 2所示, 其中SPRK方法一维最大库朗数条件可参见文献[22].
|
图 1 NSPRK方法的数值频散比率R(公式(0))曲线图,由下至上4条线分别对应库朗数:C=0.10, 0.30,0.50, 0.5163 Fig. 1 The numerical dispersion ratio R (formula (10)) of the NSPRK method for different Courant numbers. Four lines correspond to C=0.10, 0.30, 0.50, and 0.5163, respectively |
|
图 2 SPRK方法的数值频散比率R(公式(10))曲线图,由下至上5条线分别对应库朗数:C=0.10, 0.30, 0.50, 0.70, 0.8660 Fig. 2 The numerical dispersion ratio R (formula (10)) of the SPRK method for different Courant numbers. Five lines correspond to C=0. 10, 0.30, 0.50, 0.70, and 0.8660, respectively |
在频散关系图 1和图 2中, 横坐标kh表示波数与空间步长的乘积.当震源确定之后, 波数k即可确定, 在此种情况下, 空间步长h越大, 表示每个波长内取的采样点越少.从频散曲线图 1和图 2可看到, 随着kh的增大, 大多数情况下NSPRK与SPRK方法的数值频散比率R偏离1越大, 表明这两种辛方法具有相似的频散规律, 即随着h的增大, 数值频散越严重.同时, 从图 1和图 2也可看出, 对于不同的空间采样点数和不同的库朗数, NSPRK方法的数值频散比率R都在0.90和1.05之间变化, 换言之, NSPRK方法的最大频散误差小于10%, 特别地, 当达到最大库朗数时, NSPRK方法的最大数值频散误差约为3%, 而SPRK方法的最大频散误差为15.4%.
5 数值误差和计算效率由于NSPRK在空间上采用近似解析离散方法进行离散, 而在时间上使用二阶PRK格式进行离散, 因此NSPRK方法在理论上具有四阶空间精度和二阶时间精度.下面, 我们选取二维声波方程的初值问题进行数值计算以进一步研究其数值误差, 并与SPRK辛格式、二阶交错网格方法的数值误差进行比较.本文中, 我们选取的二维声波方程初值问题如下:

|
(11) |
其中c0是波速, f0是频率, θ0是初始时刻声波的入射角度.该问题有如下解析解:
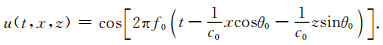
|
(12) |
定义数值解的相对误差如下:
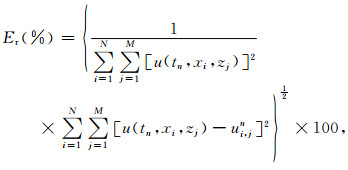
|
(13) |
其中ui, jn为数值解, u(tn, xi, zj)为精确解.选取网格点数N=M=201, 频率f0=15 Hz, 波速c0=4000m/s, θ0=π/4.
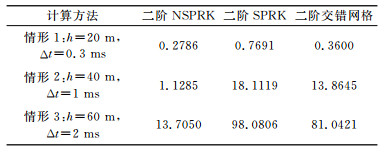
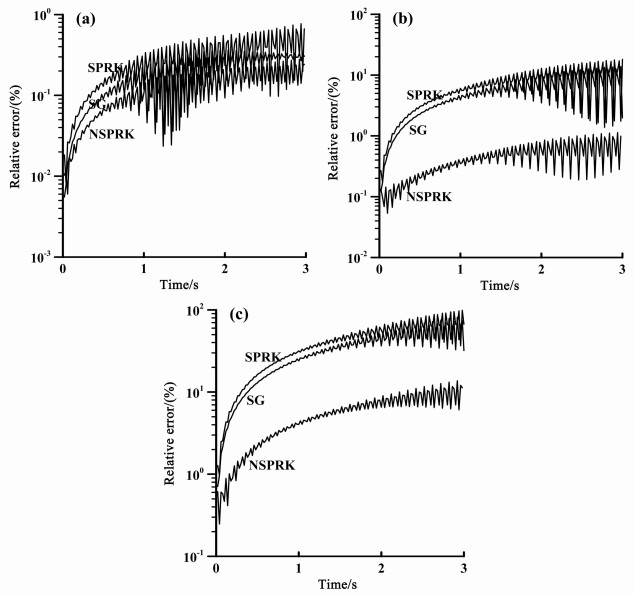
图 3给出了三种方法在三种不同情况下的相对误差曲线, 表 1为三种方法在不同情况下的最大相对误差.从误差曲线图 3(a~c)可看出, NSPRK方法、SPRK方法和交错网格方法在三种情况下的相对误差都呈现增长的趋势.对于所选取的三组计算参数, NSPRK格式的相对误差均小于二阶交错网格和SPRK辛方法的相对误差.另外, 从表 1可以看出, NSPRK方法的最大相对误差远远小于其他两种方法的最大相对误差.例如, 当h=60m, Δt=2ms时, NSPRK的最大相对误差仅是二阶交错网格方法的16.9%, 是SPRK方法的13.9%.
|
图 3 S PRK、二阶交错网格和NS PRK方法求解初值问题(1 1)时, 不同网格情况下位移u在不同时刻相对误差的比较: (a) Δ x=Δ z=h=2 0m, Δ t=0. 3m s; (b) Δ x=Δ z=h=4 0m, Δ t=1m s; (c) Δ x=Δ z=h=6 0m, Δ t=2m s Fig. 3 The relative errors of the displacement u, computed by the SPRK, second-order staggered-grid method, and the NSPRK measured by Er, are shown in a semi-log scale for the 2D initia-value problem (11), corresponding the three different cases: (a) Δ x=Δ z=h=2 0m, Δ t=0. 3m s; (b) Δ x=Δ z=h=4 0m, Δ t=1m s; (c) Δ x=Δ z=h=6 0m, Δ t=2m s |
|
|
表 1 不同计算方法在三组计算参数情况下位移u的最大相对误差比较 Table 1 Comparison of the maximum relative errors of the displacement u, computed by different methods for three cases |
下面研究NSPRK方法的波场模拟效果和计算效率.为此, 我们选取如下的二维声波方程:
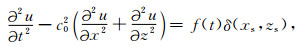
|
(14) |
其中δ(xs, zs)为除点(xs, zs)外值均为0的δ函数, 点(xs, zs)表示震源位置.
在这个数值实验中, 我们选取c0=4km/s, 计算中保持库朗数C=c0Δt/Δx≈0.285不变, 计算区域为0≤x≤10km, 0≤z≤10km, 接收器位于点(7.1km, 5km)处; 震源位于计算区域中心, 震源是主频为f0=40Hz的Ricker子波, 其随时间变化的源函数如下:
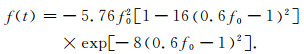
|
(15) |
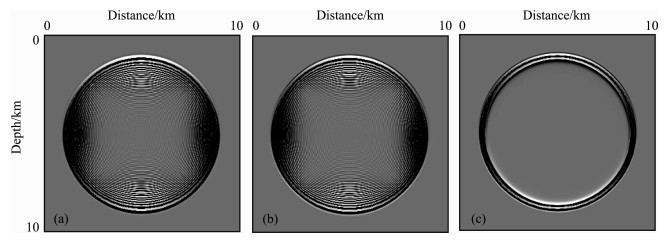
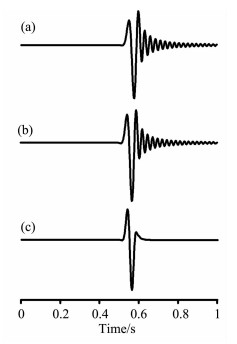
图 4给出了粗网格(Δx=Δz=28 m)情况下T=1.0s时刻的声波快照, 其中图 4(a~c)分别是由四阶Lax-Wendroff修正(LWC)格式、SPRK方法和NSPRK方法计算得到的波场快照.而图 5则分别是由这三种方法给出的在点(7.1km, 5km)处的波形记录.图 4a、4b和图 5a、5b表明四阶LWC与SPRK方法均有严重的数值频散, 而在相同条件下, 本文提出的NSPRK方法却给出了清晰的波场快照和波形(见图 4c和图 5c).由此可见, 在粗网格下, 本文的NSPRK方法比其他两种方法能更有效地压制数值频散, 获得更加精确的波场模拟结果.
|
图 4 粗网格(Δ x=Δ z=2 8m)条件下T=1. 0s时刻的声波场瞬时快照: (a)四阶LWC方法; (b) SPRK方法; (c) NSPRK方法 Fig. 4 Snapshots of acoustic wave fields at time T=1.0 sec on the coarse grid (Δx=Δz=28 m), generated by (a) the fourth-order LWC, (b) the SPRK method, and (c) the NSPRK method |
|
图 5 粗网格(Δx=Δz=28 m)条件下在接收点(7.1 km, 5.0 km)处的波形记录: (a)四阶LWC方法; (b) SPRK方法; (c) NSPRK方法 Fig. 5 The waveforms at the receiver R located at (7.1 km, 5. 0 km) on the coarse grid (Δx=Δz=28 m), generated by (a) the fourth-order LWC, (b) the SPRK method, and (c) the NSPRK method |
为了比较在消除数值频散情况下不同方法的计算效率和存储需求量, 我们分别取Δx=Δz=12 m和Δx=Δz=13m, 以消除LWC和SPRK方法在模拟波场(如图 4a和图 4b)时的数值频散.图 6给出了由四阶LWC和SPRK辛格式在精细网格条件下计算出的T=1.0s时刻的波场快照.比较图 6a、6b和图 4c, 我们可以看到它们均无可见的数值频散.但产生这些快照及波形记录的CPU时间和存储量是不一样的.在Intel (R) Core (TM)2DuoCPU、内存为2G的计算机环境下, 用四阶LWC方法和SPRK方法分别计算得到图 6a和图 6b所花费的CPU时间分别为262s和520s, 而用本文提出的NSPRK方法计算得图 4c花费的CPU时间仅为24s, 这表明, NSPRK方法的计算速度大约是四阶LWC方法的10.9倍、是SPRK方法的21.7倍.从存储量上来看, NSPRK方法与其余两种方法也显著不同, 四阶LWC方法计算得到波场快照图 6a, 需要3个834×834的存储数组, SPRK方法计算得图 6b需要3个770×770的存储数组, 而NSPRK因需要计算位移、粒子速度及其相应的空间梯度值, 需要9个存储数组以计算获得图 4c, 但每个数组大小仅为358×358.这就意味着, NSPRK方法需要的存储量只是四阶LWC方法的约55.3%、是SPRK方法的约64.9%.

|
图 6 细网格条件下T=1.0s时刻的声波场瞬时快照: (a)四阶LWC方法(Δ x=Δ z=1 2m); (b) SPRK方法(Δ x=Δ z=1 3m) Fig. 6 Snapshots of acousticwave fields at time T=1.0 sec on the fine grid, generated by (a) the fourth-order LWC (Δx=Δz=12m) and (b) the SPRK method (Δx=Δz=13m) |
为进一步研究NSPRK方法的计算效果, 本节我们选取两个不同的介质模型, 进行波场模拟.
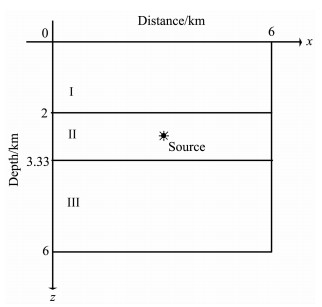
6.1 三层介质模型在这个实验中, 我们所选取的三层介质几何模型如图 7所示, 其中, 上、中、下三层介质的声波速度分别为3.0km/s、2.0km/s、4.0km/s, 震源位于第二层介质中的点(4km, 3.56km)处(见图 7中所示).实验中, 选取主频为f0=25 Hz的Ricker子波作为震源, 震源随时间变化的函数如方程(15)所示.选取空间网格步长为Δx=Δz=20 m, 时间步长为Δt=2ms, 库朗数为C=0.4.此时对应的空间采样率(一个最小波长内的采样点个数)为4.
|
图 7 三层介质模型, 计算区域为0≤x≤6km, 0≤z≤6km, 在Ⅰ、Ⅱ和Ⅲ层介质中的声波速度分别为3.0km / s, 2.0km/s和4.0km/s, 震源位于点(xs, zs)=(4km, 3.56km) Fig. 7 Geometry of the three-layer medium model, with a computational domain 0≤x≤6 km and 0≤z≤6 km. The velocities of acoustic wave in layerⅠ, Ⅱ and Ⅲ are 3.0 km/s, 2.0km/s, and 4.0 km/s, respectively. The source is located at (xs, zs)=(4 km, 3.56 km) |
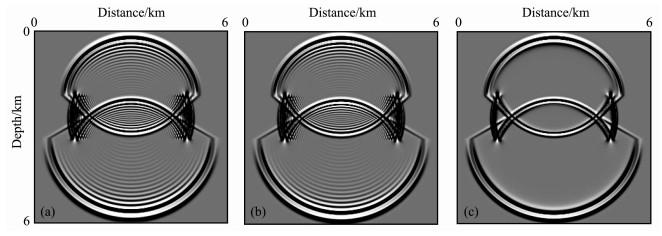
图 8为T=1.0s时刻分别由三种方法计算得到的波场快照.从图 8可以看到, 四阶LWC方法与SPRK方法的计算结果图 8a和图 8b均存在严重的数值频散, 而由NSPRK方法计算得到的波场快照图 8c则呈现了清晰的反射和透射波.表明NSPRK方法在粗网格条件下对于声波在强间断层状介质中的波传播模拟也十分有效.
|
图 8 对于三层介质模型, 粗网格(Δx=Δz=20m)条件下T=1.0 s时刻的声波场瞬时快照: (a)四阶LWC方法; (b) SPRK方法; (c) NSPRK方法 Fig. 8 Snapshots of acoustic wave fields at time T=1. 0 sec on the coarse grid (Δx=Δz=20m) for the three-layer medium model, generated by (a) the fourth-order LWC, (b) the SPRK method, and (c) the NSPRK method, respectively |
对于图 7所示的三层介质模型, 将震源置于近地表处的坐标点(xs, ys)=(4km, 0.2km), 并进行地震记录合成计算, 计算参数同上.实验中采用Yang等[23]提出的四次吸收边界条件进行边界处理, 并与使用刚性边界条件的地表地震记录进行对比.
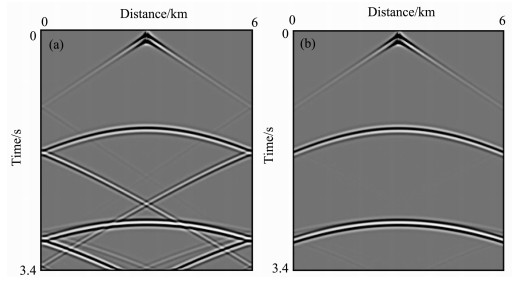
图 9为时间从0s至3.4s时刻的地表地震记录图, 其中, 图 9a和图 9b分别为采用刚性边界条件和四次吸收边界条件时的计算结果.对比图 9a和9b可以看出, 四次吸收边界条件具有良好的吸收效果.这说明NSPRK算法可以有效地与四次吸收边界条件相结合进行计算.
|
图 9 对于三层介质模型, 粗网格(Δx=Δz=20m)条件下由NSPRK方法计算得到的声波地表合成记录:(a)使用刚性边界条件的计算结果; (b)使用四次吸收边界条件的计算结果 Fig. 9 Synthetic seismograms on the surface for the three-layer medium model, generated by the NSPRK method on the grid condition Δx=Δz=20m with (a) stiff boundary condition and (b) fourth-order absorbing boundary condition |
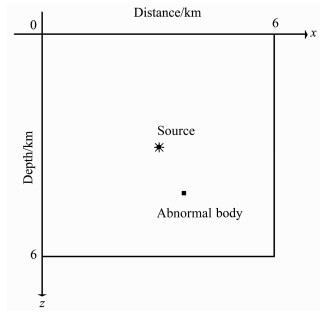
在最后的一个数值实验中, 我们选取的地质模型是一个包含有高速异常体的介质模型, 如图 10所示.其中, 异常体为边长14.4 m的正方形, 声波在背景区域中速度是4.0km/s, 在异常体中的速度为5.2km/s, 具有主频90Hz的Ricker子波源位于计算区域中心.
|
图 10 异常体模型, 计算区域为0≤x≤6km, 0≤z≤6km, 震源位于模型中心点(3km, 3km), 模型中的黑色方块区域是一个高速异常体, 位于点(3.4km, 4.2km)处, 为边长14.4m的正方形, 背景区域波速为4.0km/s, 异常体内波速为5.2km/s Fig. 10 Geometry of the abnormal body model with a computational domain 0≤x≤6 km, 0≤z≤6 km.The source is located at the center of the computational domain.The square black domain with the edge of 14.4 m is a special area with high acoustic velocity and its center is located at this point (3.4 km, 4.2 km).The wave velocity in the background area and the abnormal body is 4.0 km/s and 5.2 km/s, respectively |
我们采用NSPRK方法进行声波场模拟, 取网格步长Δx=Δz=10m, 时间步长Δt=0.75 ms, 得到T=0.7s时刻的波场快照如图 11所示(此时对应的空间采样率为4.4).从图 11可以清晰地看出异常体附近的绕射波和衍射波, 这说明在具有较高主频震源的波场模拟中, NSPRK方法可以在保持一个波长内使用较少空间点的同时, 得到清晰的计算结果, 并且有效识别介质中的微小异常体.

|
图 11 对于异常体模型, 在空间步长Δx=Δz=10m, 时间步长Δt=0.75ms条件下, 由NSPRK方法计算得到的T=0.7s时刻瞬时声波快照 Fig. 11 The snapshot of acoustic wave fields at time T=0.7 sec on the spatial increment Δx=Δz=10m and time increment Δt=0.75 ms for the abnormal body model, generated by the NSPRK |
基于波动方程的哈密尔顿系统, 本文采用二阶辛可分Runge-Kutta方法进行时间离散、近似解析离散算子近似空间微分算子, 从而得到了一种具有时间保辛性和低数值频散特性的波动方程数值格式, 即NSPRK方法, 理论分析和数值计算表明, 这种NSPRK方法时间上具有二阶精度, 空间上是四阶精度, 数值计算误差小于同阶的交错网格方法, 也小于传统SPRK辛方法的计算误差.
NSPRK辛方法具有与Yang等人发展的一类近似解析离散化方法[9, 13~15]相一致的特征, 即同时实现了位移、粒子速度及其空间梯度的计算, 即使是在空间采样率较低(每个波长4个网格点左右)的情况下, 也能有效地消除数值频散, 而传统的同阶SPRK辛方法或高阶LWC方法则必须达到每个波长具有8至9个的网格点数方可消除数值频散.另一方面, 由于本文的NSPRK辛格式是通过局部插值函数的外推方法来获得高阶空间偏导数近似值的, 所以NSPRK方法所使用的差分算子具有局部性.例如, 对于二维情况, 当计算(i, j)点处的高阶偏导数值时, 仅需要(i, j)相邻的周围8个点的信息即可获取空间高阶偏导数的近似计算公式(见附录中的(A1)~(A6)), 且可达到四阶精度, 而传统的有限差分格式则难以做到这一点.例如, 具有四阶精度的LWC方法需要(i, j)周围20个点的信息才能获得四阶精度.NSPRK辛方法所具有的局部性质有利于计算边界的处理和并行效率的提高.同时, NSPRK方法中局部差分算子的使用与地下介质中质点振动的局部性特征更为一致.
另外, 本文给出了NSPRK辛方法在一维和二维情况下的稳定性条件, 分析了SPRK方法和NSPRK方法在一维情况下的数值频散关系.结果表明, 本文提出的NSPRK方法即使在空间步长很大, 即一个波长仅有2个空间网格点时, 其最大频散误差也不超过10%, 而此时, 传统的SPRK辛方法的最大频散误差达到了15.4%, 这表明本文所提出的NSPRK辛方法比传统SPRK辛方法具有更小的数值频散.因此, 这种新的NSPRK方法比其他方法具有更快的计算速度和更小的计算机存储要求.数值实验表明, 这种NSPRK辛方法的计算速度是传统SPRK辛方法的约21.7倍, 是四阶LWC方法的约10.9倍; 而NSPRK方法的存储需求仅分别为SPRK方法的64.9%和四阶LWC方法的55.3%.
附录 二维空间离散化近似计算公式为了计算哈密尔顿系统(8)中的高阶空间偏导数, 与一类NADM[9, 11~13]方法的处理方式一样, 引入如下插值函数:
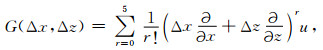
|
其中Δx, Δz分别是空间x和z方向的网格步长, u为位移函数.通过上述插值函数, 使用外推方法即可获得包含于方程(8)中高阶空间偏导数的近似计算公式.为方便起见, 这里列出本文中所使用的这些高阶偏导数的近似计算公式[9]:
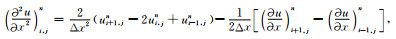
|
(A1) |

|
(A2) |
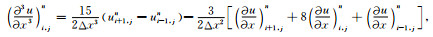
|
(A3) |

|
(A4) |

|
(A5) |
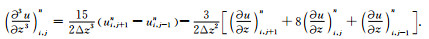
|
(A6) |
用v(v为粒子速度)代替上述公式中的u, 即可得到关于v的高阶空间偏导数的近似公式, 此处略去.
| [1] | Kelly K R, Wave R W, Treitel S. Synthetic seismograms:a finite-difference approach. Geophysics , 1976, 41: 2-27. DOI:10.1190/1.1440605 |
| [2] | Dablain M A. The application of high-order differencing to the scalar wave equation. Geophysics , 1986, 51: 54-66. DOI:10.1190/1.1442040 |
| [3] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(3): 411–419. Dong L G, Ma Z T, Cao J Z, et al. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese) , 2000, 43(3): 411-419. |
| [4] | Komatitsch D, Vilotte J P. The spectral element method:an efficient tool to simulate the seismic responses of 2D and 3D geological structures. Bull. Seism. Soc. Am. , 1998, 88: 368-392. |
| [5] | Chen K H. Propagating numerical model of elastic wave in anisotropic in homogeneous media-finite element method. Symposium of 54th SEG , 1984, 54: 631-632. |
| [6] | Cerveny V, Firbas P. Numerical modeling and inversion of travel-time seismic body waves in inhomogeneous anisotropic media. Geophys. J. R. Astr. Soc. , 1984, 76: 41-51. DOI:10.1111/j.1365-246X.1984.tb05020.x |
| [7] | Yang D H, Song G J, Lu M. Optimally accurate nearly analytic discrete scheme for wave-field simulation in 3D anisotropic media. Bull. Seism. Soc. Am. , 2007, 97(5): 1557-1569. DOI:10.1785/0120060209 |
| [8] | Fei T, Larner K. Elimination of numerical dispersion in finite difference modeling and migration by flux-corrected transport. Geophysics , 1995, 60: 1830-1842. DOI:10.1190/1.1443915 |
| [9] | Yang D H, Teng J W, Zhang Z J, et al. A nearly-analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bull. Seism. Soc. Am. , 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [10] | Zhang Z J, Wang G J, Harris J M. Multi-component wave-field simulation in viscous extensively dilatancy anisotropic media. Phys. Earth Planet. Inter. , 1999, 114: 25-38. DOI:10.1016/S0031-9201(99)00043-6 |
| [11] | Zheng H S, Zhang Z J, Liu E. Non-linear seismic wave propagation in anisotropic media using flux-corrected transport technique. Geophys. J. Int. , 2006, 165: 943-956. DOI:10.1111/gji.2006.165.issue-3 |
| [12] | Kondoh Y, Hosaka Y, Ishii K. Kernel optimum nearly-analytical discretization algorithm applied to parabolic and hyperbolic equations. Computers Math. Appl. , 1994, 27(3): 59-90. DOI:10.1016/0898-1221(94)90047-7 |
| [13] | Yang D H, Peng J M, Lu M, et al. Optimal nearly analytic discrete approximation to the scalar wave equation. Bull. Seism. Soc. Am. , 2006, 96(3): 1114-1130. DOI:10.1785/0120050080 |
| [14] | Yang D H, Song G J, Chen S, et al. An improved nearly analytical discrete method:an efficient tool to simulate the seismic response of 2-D porous structures. J. Geophys. Eng. , 2007, 4: 40-52. DOI:10.1088/1742-2132/4/1/006 |
| [15] | 王磊, 杨顶辉, 邓小英. 非均匀介质中地震波应力场的WNAD方法及其数值模拟. 地球物理学报 , 2009, 52(6): 1526–1535. Wang L, Yang D H, Deng X Y. A WNAD method for seismic stress-field modeling in heterogeneous media. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1526-1535. |
| [16] | Yang D H, Wang N, Chen S, Song G J. An explicit method based on the implicit Runge-Kutta algorithm for solving the wave equations. Bull. Seism. Soc. Am. , 2009, 99(6): 3340-3354. DOI:10.1785/0120080346 |
| [17] | 罗明秋, 刘洪, 李幼铭. 地震波传播的哈密顿表述及辛几何算法. 地球物理学报 , 2001, 44(1): 120–127. Luo M Q, Liu H, Li Y M. Hamiltonian description and symplectic method of seismic wave propagation. Chinese J. Geophys. (in Chinese) , 2001, 44(1): 120-127. |
| [18] | 冯康, 秦孟兆. 哈密尔顿系统的辛几何算法. 杭州: 浙江科学技术出版社, 2003 : 185 -278. Feng K, Qin M Z. Symplectic Geometric Algorithms for Hamiltonian Systems (in Chinese). Hangzhou: Zhejiang Science & Technology Press, 2003 : 185 -278. |
| [19] | Ruth R D. A canonical integration technique. IEEE Trans. Nucl. Sci. 1983, NS-30, No. 4:2669~2671 |
| [20] | 曾文平, 孔令华. 辛算法的发展历史与现状. 华侨大学学报(自然科学版) , 2004, 25(2): 113–117. Zeng W P, Kong L H. History and present state of symplectic algorithm. J. Huaqiao Univ. (Natr. Sci.) (in Chinese) , 2004, 25(2): 113-117. |
| [21] | 孙耿. 波动方程的一类显式辛格式. 计算数学 , 1997, 1: 1–10. Sun G. A class of explicitly symplectic schemes for wave equations. Comput. Math. (in Chinese) , 1997, 1: 1-10. |
| [22] | Qin M Z, Zhang M Q. Multi-stage symplectic schemes of two kinds of Hamiltonian systems for wave equations. Computers Math. Applic. , 1990, 19: 51-62. |
| [23] | Yang D H, Wang S Q, Zhang Z J, et al. N-times absorbing boundary conditions for compact finite-difference modeling of acoustic and elastic wave propagation in the 2D TI medium. Bull. Seism. Soc. Am. , 2003, 93(6): 2389-2401. DOI:10.1785/0120020224 |
 2010, Vol. 53
2010, Vol. 53