2. 西南石油大学理学院, 成都 610500
2. College of Sciences, Southwest Petroleum University, Chengdu 610500, China
有限差分方法是地震波场模拟和地震偏移中应用最广泛的数值方法.数值频散是有限差分方法的固有现象, 它严重制约了有限差分方法在大尺度地震波场、复杂区域地震波场模拟、地震偏移等研究中的应用.大量研究表明, 对于某种特定的差分方法, 当采用过小的采样率(最小主波长/空间网格步长)时, 将会因采样不足而使得模拟结果(波场快照、地震合成记录等)中出现伪波(数值频散), 从而降低地震波场信息的分辨度; 而采用过大的采样率, 虽然可以消除数值频散, 提高地震波场信息的分辨度, 但会因使用过小的空间和时间步长而导致计算效率的降低, 并增大计算所需的存储量.因此, 只有根据地质模型的特征, 在不同的计算区域采用不同的采样率, 才能保证差分方法在消除数值频散的前提下达到优化的计算效率和存储效率.
在使用有限差分方法模拟地震波场时, 通常情况下, 我们都是在整个计算空间上使用一致的空间网格来划分计算区域.对于均匀介质情况, 这样的处理是合适的.但在很多实际问题中, 地下介质存在波速变化较大的异常区(如含薄互层、低速区、含盐丘类高速区等复杂地质构造).对于存在异常区的地下介质, 一致网格算法的有效性和可行性受到很大限制[1].此时, 若以高速区为参照而采用粗网格进行波场模拟, 则在低速区域, 由于采样不足, 导致波场或地震记录分辨率不高, 数值频散严重等, 无法准确反映地下介质的精细结构; 若以低速区为参照采用细网格模拟, 则在高速区存在过采样等问题, 从而导致计算速度太慢、存储量太大, 甚至会因内存需求太大、计算速度过慢等, 最终使得计算无法进行.
在进行大尺度和复杂地质条件下的波场模拟时, 为了兼顾计算效率和模拟效果, Moczo[2]首次提出了非一致网格算法的思想, 并将这种想法应用于二维SH地震波场模拟, Jastram等[3]将非一致网格算法应用于弹性波场模拟.非一致网格算法的计算方式打破了传统的固定网格波场模拟模式, 其基本思想是:根据介质速度大小或实际计算的需要等, 在不同的计算区域选择不同的离散网格步长.简单地说, 就是在高速区采用粗网格, 在低速区采用细网格.这样做, 一方面可以在减少计算量和存储量的同时又能有效捕捉地球介质的精细结构; 另一方面, 实际介质中的地震波场模拟, 也需要使用非一致网格来处理内间断面或起伏地表, 以便减小计算误差、提高波场分辨率.在国内, 孙卫涛等[4]、李胜军等[5]、朱生旺等[6]、黄超等[7]也相继将非一致网格剖分方法应用到了地震波场的数值模拟中.
在使用差分方法进行波场模拟的数值计算中, 除了网格划分的选择问题之外, 还有数值计算方法的选择问题.我们知道, 无论是使用一致网格还是使用非一致网格来划分, 选择一种好的差分格式是很重要的, 甚至可以说是最重要的.一种能在粗网格或层间速度存在大反差的情况下仍然可以有效压制数值频散的差分格式, 将会在很大程度上提高计算效率、节省计算存储空间.通常情况下, 压制数值频散有两种基本途径, 一种是加细网格, 另一种是提高计算方法的精度.但是加密网格必须采用高采样率, 这样会导致计算CPU时间和存储需求量剧增, 是一种不可取的方法.而传统的高阶有限差分格式(Lax-Wendroff Correction (LWC))[8]、交错网格(Staggered Grid (SG))等方法[9]在空间上使用较多的网格点来获得高精度, 以达到减小数值频散的目的.对于这种高精度差分方法, 由于在每个方向上使用了较多网格点, 使得边界处理较为不便, 且容易降低边界点的计算精度和计算方法的稳定性.边界点计算精度和计算方法稳定性的降低又会反过来影响计算区域内部节点的计算精度和稳定性, 从而使得整个计算结果不能尽如人意.同时, 每个方向上使用较多的网格点, 也会使得并行计算时不同进程之间的通信量大大增加, 从而导致并行计算效率的严重降低.
杨顶辉等[10~13]提出的近似解析离散化及其改进方法是一类新的扰动差分计算方法.这类方法首先利用偏微分方程的时空转化关系, 将波位移的时间高阶偏导数转化为位移的空间高阶偏导数[8].然后对波位移的高阶空间偏导数, 不仅使用位移, 而且也使用位移的梯度场来共同构造波位移的高阶空间偏导数.这样的处理充分利用了梯度所反映的波形走势之物理规律, 保留了更多的重要波场信息, 从而使得这类近似解析离散化方法即使在粗网格条件下也能有效地压制数值频散, 极大地提高了波场模拟的计算效率、节省了存储空间.目前, 这类方法已经成功应用到单相声波、弹性波[11]和双相弹性波方程[12]的波场模拟.但对于这类方法的研究和应用目前还局限于一致网格剖分计算区域上的情况.
本文的主要目的是实现加权近似解析离散化(WNAD)方法的非一致网格算法, 以达到在保持高分辨率的条件下, 实现计算效率和存储效率的进一步提高.为此, 我们首先应用分片插值多项式插值方法获得了WNAD方法的非一致网格算法, 然后, 选取含低速层模型和起伏地表模型, 通过波场模拟计算来验证算法的有效性和可行性.
2 加权近似解析离散化方法的非一致网格算法在二维弹性介质中, 弹性波方程可以写为

|
(1) |
其中cijkl(x, y, z)是一个四阶对称弹性张量, ui为第i个方向上的波位移分量, fi为第i个方向上的体力分量.变量上的"·"表示对时间的一阶导数, 下标中记号", j"表示对xj求偏导.
2.1 基本的加权近似解析离散化方法
为了叙述方便, 我们引入记号U={u1, u3, u1, 1, u1, 3, u3, 1, u3, 3}T表示波位移及其梯度组成的向量, 变量

与Yang等[10]的思路一致, 利用4次截断的Taylor公式展开, 可以得到由第n时间层相关量所表示的第n+1时间层的位移和粒子速度表达式分别为:

|
(2) |
和

|
(3) |
对于公式(3), 考虑到已由公式(2)计算获得了最新的粒子速度Wi, jn+1, 因此, 我们可借鉴求解线性代数方程组Gauss-Seidel方法[14]的类似思想, 采用Wi, jn+1和Wi, jn的一个加权组合来替代公式(3)中的Wi, jn, 以谋求一个收敛更快的算法, 从而得到新的位移更新公式:

|
(4) |
其中ω为一加权常数, 满足0≤ω≤1.
若联合使用公式(2)和(4)以实现时间推进计算的话, 显然首先必须计算U、W和P对时间的高阶偏导数.如果直接离散公式(2)和公式(4)中的高阶时间偏导数, 则需要存储多个时间层上的波位移、粒子速度及其梯度值, 内存需求量大.注意到在公式(2)和(4)中, 只含有波位移和粒子速度关于时间的偶数阶偏导数, 所以我们可采取Dablain [8]的方法, 利用方程(1), 首先将时间的高阶偏导数转化为空间的高阶偏导数, 然后再利用Yang等[10, 12]给出的空间高阶偏导数的逼近公式来计算公式(2)和(4)中所涉及到的这些高阶空间偏导数.
2.2 非一致网格算法本文中的非一致网格指的是根据实际计算需要, 在不同的计算区域使用不同的网格剖分.具体说, 就是在相对高速区采用粗网格, 在相对低速区采用细网格, 使其计算结果既可以尽可能地提高分辨率, 又可以尽可能地降低计算时间和计算存储量.其算法实现的关键在于解决好网格变化过渡区域的联结问题[7].保证在过渡区域不因网格尺度变化而产生明显的数值频散或者人工绕射等附加计算噪声.下面我们分别就一维和二维情况给出加权近似解析离散化方法在过渡区域的数值计算公式, 以实现WNAD方法的非一致网格算法.
2.2.1 一维情形图 1给出了一维情况下不同区间使用不同网格步长的剖分示意图.其中, 网格点稀疏区间表示波速相对较高的区间.在此区间, 由于波速较大, 使得在同样的震源频率下, 在该区间内传播的波具有相对较大的波长.所以我们可以使用粗网格对此区间进行空间剖分, 记网格步长为: Δx=h1; 而图中所示网格点密集区间表示波速相对较低的区间.在此区间, 由于波速较低, 使得在同样频率下, 在此区间传播的波具有相对较小的波长, 所以我们需要使用细网格对此区间进行空间剖分, 记其网格步长为Δx=h2.为了计算下一时间层上弹性分界面处的位移和梯度值, 需要在分界面高速区一侧加入插值点.由于加权的近似解析离散化方法每个方向只需要使用3个网格点, 所以每个方向只需要插入一个插值点C1和C2(如图 1所示).同时, 由于加权的近似解析离散化方法在计算节点处位移的同时, 也计算了节点处的空间偏导数, 我们可以很容易地获得精度更高、光滑性更好的埃尔米特插值多项式.

|
图 1 一维情形下的非一致网格示意图 Fig. 1 The sketch of mom-umiform grids for the 1D case |
假设插值点C1左右两个节点A、B处的位移和梯度分别为uin, (ux)in和ui+1n, (ux)i+1n, 同时不妨设AB之间的埃尔米特插值多项式为H(x)=ax3 + bx2+cx+d, 则节点处的位移和梯度与插值多项式之间满足关系式:

|

|
联立并求解线性方程组, 可得

|
所以C1处的位移和梯度分别为
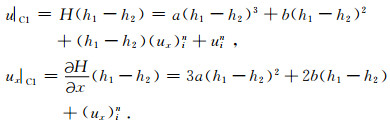
|
下面我们以图 2a中的模型为例(阴影部分为低速区, 其他的地方为正常速度区)来说明如何实现二维非一致网格算法.

|
图 2 二维非一致网格示意图 (a)网格剖分示意图; (b)三角形插值计算示意图. Fig. 2 The sketch of mom-umiform grids for the 2D case (a) Grid-partition; (b) The interpolation sketch based on the triangle units. |
首先, 我们用一个矩形区域覆盖低速异常区, 并使用细网格(Δx=Δz=h2)对此矩形区域进行空间剖分, 而其他区域使用粗网格(Δx=Δz=h1)进行空间剖分, 如图 2a所示.其次, 为了能对矩形边界处节点信息进行更新, 我们需要在矩形边界外层加入插值节点(图 2a中用小三角形表示).最后, 给出插值点的插值公式.这样我们即可得到二维非一致网格算法.
为了实现非一致网格上的迭代计算, 需要将过渡区域中属正常区的部分再按三角网格进行网格划分(如图 2所示), 并将所有插值节点分成各个子区域单独计算.在每个三角形网格内插值, 至少应该有4个点(三角形的三个顶点、所求插值节点在分界面上的投影点)的值(位移、梯度)是已知的.
下面以其中一个三角形(图 2b)为例说明如何得到插值点E的位移和梯度.设图 2b中, A点的位移和两个梯度分量分别为ui, jn, (ux)i, jn, (uz)i, jn, B点的位移和两个梯度分量分别为ui+1, jn, (ux)i+1, jn, (uz)i+1, jn, C点的位移和两个梯度分量为ui, j+1n, (ux)i, j+1n, (uz)i, j+1n, D点的位移和两个梯度分量为uDn, (ux)Dn, (uz)Dn.且AD的距离为mh2, DE的距离为h2.假设由插值节点A、B、C、D确定的三角形ABC内部的一个三次埃尔米特插值多项式为:

|
(5) |
类似于一维情形, 插值多项式和插值节点之间存在如下关系:

|
由此可解出

|
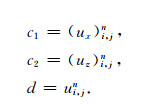
|
将上述系数代入三次埃尔米特插值多项式(5), 则所求插值点E处的位移和梯度分别为

|
对于含有低速异常区、起伏地表等构造复杂的地球介质, 使用非一致网格上的加权近似解析离散化方法进行波场模拟, 可以快速高效地得到具有较高分辨率的地震波场快照、地震记录等, 从而有利于我们研究复杂地球介质中的波传播规律.在本节, 我们分别设计了模型1(含低速薄层的三层模型)和模型2(起伏地表+含速度异常区模型)来说明本文所提出的非一致网格算法的有效性和优越性.在我们所做的数值实验中, 所有计算均是在一台具有Intel Core 2 Duo CPU 2.33G、1G内存、操作系统为Ubuntu 8.04的PC机上进行.
3.1 模型1在第一个模型实验中, 我们选择的是一个简单的、含有低速薄层的层状介质模型, 如图 3所示.各层参数如表 1.由表 1知, 低速层厚度只有整个计算区域厚度的5%, 速度为背景区域速度的1/4.也就是说, 层间速度反差为4倍.计算区域大小为10km×10km, 震源位于(5km, 5.75km), 震源主频f0=40Hz, 随时间变化的震源函数为:

|

|
图 3 含低速薄层的三层模型(模型1) Fig. 3 Three-layer model with a thin low-velocity interlayer (model 1) |
|
|
表 1 模型1参数 Table 1 The parameters of model 1 |
的Rick子波.
图 4(a、b、c)分别为按高速区采样得到的粗网格(Δx=Δz=25 m)、按低速区采样得到的细网格(Δx=Δz=6.25m)、以及采用非一致网格剖分(高速区计算网格为Δx=Δz=25 m, 低速区计算网格为Δx=Δz=6.25m)计算得到的0.9s时刻的波场快照.从图 4可以看到:若网格剖分按高速区进行空间采样(图 4a), 虽然计算速度快、所需内存少, 但是由于在低速区采样不足, 导致波场模拟结果的分辨率不高, 部分反射波、透射波、转换波不够清晰、层间多次波无法分辨; 而网格剖分按低速区采样计算得到的波场快照(图 4b)和使用非一致网格计算得到的波场快照(图 4c)都十分清晰, 可以看到各种折射波、反射波、转换波、层间多次波等.同时, 我们从采用非一致网格算法计算得到的波场快照图 4c看到, 在网格步长发生变化的联结区没有产生人为的数值散射.

|
图 4 对模型1在不同网格情况下0.9 s时刻的波场快照比较(a)粗网格; (b)细网格; (c)非一致网格. Fig. 4 The comparison of wave-field snapshots for model 1 at 0.9 sec on the coarse grid (a)' fine grid (b) and non-uniform grid (c) |
虽然按低速区采样得到的波场快照(图 4b)和采用非一致网格得到的结果(图 4c)都具有分辨率高、波形清晰等特点, 但是由于一致细网格在高速区内单位波长的采样点数远超过差分格式能够消除数值频散所需要的最低采样点数, 这使得整个模拟所需要的存储量和计算量较大; 而非一致网格算法在不同的计算区域使用了不同的空间步长, 使得计算量和内存需求量大幅下降.事实上, 使用一致细网格计算得到图 4b需要23324s的CPU计算时间, 而使用非一致网格算法计算得到图 4c只需要2491s.这就意味着, 使用非一致网格算法进行波场模拟的计算速度是使用一致网格(按低速区采样)算法情况下的9.4倍, 同时非一致网格的内存需求量只需使用一致网格情况下内存需求量的11.7%.这说明非一致网格算法能兼顾粗网格情况下的高效和细网格条件下的精确, 从而使得其达到了高效性和精确性的优化统一.
3.2 模型2为了考察非一致网格算法在具有起伏地表、含速度异常区等复杂介质情况下波场模拟的有效性, 我们设计了图 5所示的模型2.在模型2中, 地表左边有光滑的隆起和凹陷, 地表右侧有一个连续的、向下的倾斜面; 模型基质(背景)为花岗岩, 其物性参数为vp=5.5km/s, vs=3.0km/s, ρ=2.63g/cm3; 在模型右下方有一个充满水的正方形速度异常区, 其物性参数为vp=1.5km/s, vs=0km/s, ρ=1.0g/cm3.震源位于(3.75km, 3km), Rick子波主频为30Hz, 其随时间变化的震源函数与模型1中的震源函数一致.

|
图 5 复杂地质构造模型(模型2) Fig. 5 The complicated geological structure (model 2) |
在背景区域采用步长为25 m的空间网格, 在低速区采用步长为12.5 m的空间网格, 边界处理采用4次吸收边界条件[15], 使用非一致网格加权近似离散化方法计算得到0.7s时刻的波场快照如图 6所示.从快照上可以看到, P波和S波在物性界面(花岗石和水的交界面)产生反射和折射, 由于S波不能在液体中传播, 所以只能在含水区域观测到直达P波的透射波Pp波、S波的转换波Sp波.在固体区域可以观测到: P波在物性界面产生的反射波PP波和转换波PS波; S波在物性界面产生反射波SS波和转换波SP波.在地表附近可以观测到P波在地表反射产生的PP波和转换波PS波.由于此时S波尚未到达地表, 所以S在地表无反射和转换波产生.由于模型2中的地表是起伏地表, 所以在地表观测到了各种绕射波, 特别是在地表中部隆起区域, 各种波在传播中互相干涉、叠加, 使得波形变得非常复杂, 产生一系列波前能量"焦点", 具有明显的聚焦现象[1]; 相对于固体区域, 含水区域波形较弱, 能量衰减较快.由于本模型构造复杂, 直达P波以及地表反射PP波、转换PS波在地表多次反射、转换, 导致很难一一辨认波场中的每一波形, 但是整个波场非常清晰, 无明显的数值频散.这些都说明非一致网格上的WNAD方法可以清晰、全面、正确地模拟复杂介质中的地震波传播.在人工边界处, 对人工边界反射波的吸收很好, 说明本文所使用的4次吸收边界条件与非一致网格WNAD算法的耦合是有效的.

|
图 6 对模型2在0.7 s时刻的波场快照 Fig. 6 The wave-field snapshot at 0.7 s for model 2 |
本文给出了非一致网格上的加权近似解析离散化算法.这种方法在特殊区域, 如复杂几何界面、低速异常区、物理属性间断处等区域使用加密的精细网格, 而在其他计算区域则使用粗网格.在这种网格剖分意义下, 本文发展的非一致网格WNAD算法仍能获得与精细网格条件下相一致的计算结果, 但它们的计算时间和所需计算存储量却相差很大.换句话说, 与规则一致细网格条件下的计算相比, 非一致网格WNAD算法能有效地降低计算内存需求量、提高计算效率, 能够很好地实现含薄互层速度异常区、起伏地表等复杂地下介质中地震波场数值模拟的高精度、高分辨率快速计算.为我国复杂地区地震波传播数值模拟提供了一种十分有效的正演模拟技术.
| [1] | 牟永光, 裴正林. 三维复杂介质地震数值模拟. 北京: 石油工业出版社, 2005 . Mou Y G, Pei Z L. Seismic Numerical Modeling for 3-D Complex Media (in Chinese). Beijing: Petroleum Industry Press, 2005 . |
| [2] | Moczo P. Finite-difference technique for SH waves in 2-D media, using irregular grids:application to the seismic response problem. Geophys. J. Int. , 1989, 99: 321-329. DOI:10.1111/gji.1989.99.issue-2 |
| [3] | Jastram C, Tessemer E. Elastic modeling on a grid of vertically varying spacing. Geophys. Prosp. , 1994, 42: 357-370. DOI:10.1111/gpr.1994.42.issue-4 |
| [4] | 孙卫涛, 杨慧珠. 各向异性介质弹性波传播的三维不规则网格有限差分方法. 地球物理学报 , 2004, 47(2): 332–337. Sun W T, Yang H Z. A 3D finite difference method using irregular grids for elastic wave propagation in anisotropic media. Chinese J. Geophys. (in Chinese) , 2004, 47(2): 332-337. |
| [5] | 李胜军, 孙成禹, 倪长宽, 等. 声波方程有限差分数值模拟的变网格步长算法. 工程地球物理学报 , 2007, 4(3): 207–212. Li S J, Sun C Y, Ni C W, et al. Acoustic equation numerical modeling on a grid of varying spacing. Chinese J. Eng. Geophys. (in Chinese) , 2007, 4(3): 207-212. |
| [6] | 朱生旺, 曲寿利, 魏修成, 等. 变网格有限差分弹性波方程数值模拟方法. 石油地球物理勘探 , 2007, 42(6): 634–639. Zhu S W, Qu S L, Wei X C, et al. Numeric simulation by grid-various finite-difference elastic wave equation. Oil Geophys. Prosp. (in Chinese) , 2007, 42(6): 634-639. |
| [7] | 黄超, 董良国. 可变网格和局部时间步长的高阶差分地震波数值模拟. 地球物理学报 , 2009, 52(1): 176–186. Huang C, Dong L G. High-order finite-difference method in seismic wave simulation with variable grids and local time-steps. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 176-186. DOI:10.1002/cjg2.v52.1 |
| [8] | Dablain M A. The application of high-order differencing to the scale wave equation Laser. Geophysics , 1986, 51(1): 54-66. DOI:10.1190/1.1442040 |
| [9] | Virieux J. SH-wave propagation in heterogeneous media:Velocity-stress finite-difference method. Geophysics , 1984, 49(11): 1933-1957. DOI:10.1190/1.1441605 |
| [10] | Yang D H, Teng J, Zhang Z J, et al. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bull. Seis. Soc. Am. , 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [11] | Yang D H, Lu M, Wu R S, et al. An optimal nearly analytic discrete method for 2D acoustic and elastic wave equations. Bull. Seis. Soc. Am. , 2004, 94(5): 1982-1991. DOI:10.1785/012003155 |
| [12] | Yang D H, Song G J, Chen S, et al. An improved nearly analytical discrete method:an efficient tool to simulate the seismic response of 2-D porous structures. J. Geophys. Eng , 2007, 4: 40-52. DOI:10.1088/1742-2132/4/1/006 |
| [13] | 王磊, 杨顶辉, 邓小英. 非均匀介质中地震波应力场的WNAD方法及其数值模拟. 地球物理学报 , 2009, 52(6): 1526–1535. Wang L, Yang D H, Deng X Y. A WNAD method for seismic stress-field modeling in heterogeneous media. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1526-1535. |
| [14] | Demmel J W. Applied Numerical Linear Algebra. Philadelphia: SIAM, 1997 . |
| [15] | Yang D H, Wang S Q, Zhang Z J, et al. n-times absorbing boundary conditions for compact finite-difference modeling of acoustic and elastic wave propagation in the 2D TI medium. Bull. Seis. Soc. Am. , 2003, 93(6): 2389-2401. DOI:10.1785/0120020224 |
 2010, Vol. 53
2010, Vol. 53



