2. 武汉大学电子信息学院, 武汉 430079
2. School of Electronic Information, Wuhan University, Wuhan 430079, China
重力波活动是中高层大气中最重要的动力学过程之一,对于局地大气的暂态结构以及全球大气环流都有着非常重要的影响[1~3].重力波在大气中传播时,背景大气垂直方向上浮力频率的梯度或者风场的剪切都可能俘获重力波形成导制传播,其中风剪切起主导作用的波导称为多普勒波导,浮力频率梯度起主导作用的波导为温度波导[4~6].
近十几年来在中层大气中已经观测到了非常多的导制传播事件,研究表明,在温度梯度较大的低热层、梯度稍小的平流层,都存在着长期而稳定的温度波导结构;而风剪切形成多普勒波导一般具有局地性,存在的时间较短[7~11].
波导结构在很多方面都影响着重力波的活动,因此重力波在温度波导中的传播特性和传播模式也一直吸引着科学家们的关注[12~16],早期的模式研究中波模的求解多采用全波解计算,方法非常繁琐,而且得不到解析的色散关系[6, 17].Nappo[18]和Seyler[19]分别在大气浮力频率水平均匀分层情况下,讨论了温度波导中的重力波的传播,前者考虑的是以地面为波导下边界的温度波导模型,且假定分层大气上层的浮力频率为零;而后者的模型在垂直方向上采用了周期性边界条件,以保证波导区域内重力波总能量的守恒.这些模型直接应用于实际中层大气时均有一定的局限性,且两种模型的分析只涉及到重力波导制传播时的非对称模式,未涉及到对称传播模式.
本文从模式分析和数值模拟两个方面研究了重力波在中层大气温度波导中的各类传播模式,既包含非对称模式,也包含对称模式.给出了更符合中层大气实际情形的温度波导模型,波导区域内允许波能量的泄露,模式分析也因而能够考虑到重力波的部分导制传播.模式分析给出了重力波在各种导制传播模式下的色散方程,并采用离散的方法求解色散方程,获得了重力波部分导制传播时的色散曲线以及水平传播速度等参数.数值模拟采用全非线性的FICE格式研究了温度波导对低层大气不同扰动的响应,成功地展现了重力波部分导制传播时的对称与非对称波包结构,并进行了详细的比较和讨论.
本文余下部分结构安排如下:第2节为重力波在温度波导内的传播模式分析,第3节对重力波包在温度波导中的传播进行了数值模拟,第4节对模拟结果进行分析和讨论,并和模式分析的预测进行了比较,第5节为结论.
2 传播模式解析分析本文将重力波的温度波导模型扩展到中层大气,此时大气中浮力频率水平均匀分层,垂直分布形式为[18~20]
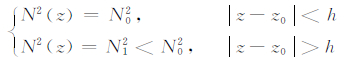
|
(1) |
其中z为垂直方向坐标,z0为温度波导的中心高度,h为温度波导的半宽,浮力频率的分布关于波导中心高度z0对称,在波导区域内大气浮力频率为N0,在波导区域外大气浮力频率为N1.
在背景风速为零情况下,Taylor-Goldstein方程(2)可以简化为[18]

|
(2) |
其中ω为重力波频率,k为水平波数,ŵ为密度加权的垂直风扰动.ŵ与垂直风扰动w′的关系满足

|
其中m为重力波的垂直波数,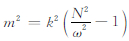
重力波导制传播时,波频率满足N1<ω<N0,令z′=z-z0,控制方程可写为

|
(3) |
此时特征函数解的形式为

|
(4) |
其中
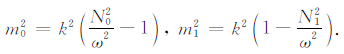
|
(5) |
重力波完全导制传播时,垂直方向上波能量被全部局限在波导区域内,可知ŵ|Z'=±h,因此有
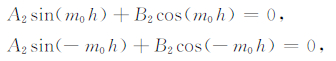
|
求解可得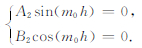

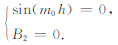
对称模式: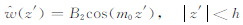
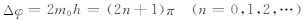
非对称模式: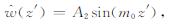
重力波完全导制传播时,能量在垂直方向上没有泄露,所有的能量都被一直局限在波导内,该条件比较苛刻,此时相位变化量Δφ恰好为π的整数倍,ŵ|Z'=±h0.实际大气中更普遍的情况为重力波在波导中传播时存在着轻微而缓慢的能量泄露,但波包在垂直方向上可以被限制在波导范围内达相当长的时间,依然结构清晰,水平方向上也因此能够传播到相当远的距离,这样的情形即为部分导制传播.对于能量泄露缓慢部分导制传播,可知此时相位变化满足Δφ ≈(n+1)π,因此有ŵ|z’=±h≈0.对于重力波的导制传播,无论是对称模式还是非对称模式,我们都只需要考虑z′≥0时的情况.
对于重力波的部分导制非对称模式,此时Δφ ≈(2n+2)π,特征函数解的形式为
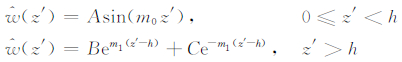
|
(6) |
在z′=h处,由动力学和运动学边界条件,可知ŵ和它的导数都是连续的,即
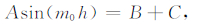
|
(7) |

|
(8) |
将(7)式乘以m1再与(8)式相加可得
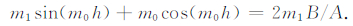
|
(9) |
在z′ > h高度以上,考虑到导制传播情况下重力波的振幅会随着高度衰减,因此有m1 > 0,B=0,代入(9)式可得
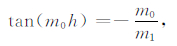
|
将m0和m1的表达式(5)代入,可得
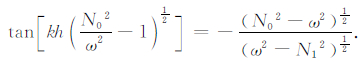
|
(10) |
(10)式和(15)式分别为非对称模式和对称模式下,重力波在温度波导中被部分导制传播时的色散方程.方程左边的正切函数为周期函数,对于给定的水平波数会有无数个ω满足方程,每个不同的ω对应着不同的垂直波数,也对应着不同的波模.
2.3 色散方程的离散求解根据重力波在波导中传播时的色散方程(10)与(15),我们也可以获得该重力波相关参量(如相速度、群速度)的表达式,然而由于方程的形式复杂,而且当ω=N1或者ω=N0时,色散方程的右侧可能会出现奇点,解的解析形式难以获得.但我们可以用离散的方法画出基于该方程的频率与水平波数散点图,并算出相速度、群速度等参量.
中层大气温度波导结构可近似由波导半宽h,俘获层大气浮力频率N0,消散层大气浮力频率N1三个参数决定,由色散方程(10)与(15)也可知道重力波在波导中的传播特性与波导中心所处的高度无关.本文选取一个具体的温度波导模型,通过对色散方程离散的求解,讨论重力波在其中的传播模式.波导结构参数的选取为N1=1.23×10-2rad/s,N0=2.61×10-2rad/s(对应的Brunt周期分别为7.5min和4min),z0=30km,h=10km.参数的选择参考了大气中平流层附近可能出现的温度波导结构,对于实际大气中浮力频率随高度的分布做了分段常数近似[19~21].而对于中层大气中其他高度上可能存在的温度波导,如中层顶处的温度梯度结构,或者由于较强的逆温层结构所形成的温度波导等,只需要对波导宽度及浮力频率参数进行适当的调整,本文的模型分析依然适用.
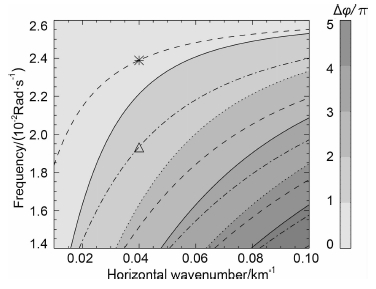
图 1为不同模式下重力波在温度波导中传播时的色散关系曲线,实线和点线分别代表完全导制情况下的对称模式和非对称模式,虚线和点划线分别代表部分导制情况下的对称模式和非对称模式(据(10)和(15)式求解而来).由图 1可知该温度波导中可能存在重力波的多种导制传播模式,而实际大气中n较小的模式更容易出现,因此本文将着重讨论重力波的基模导制传播(n=0).下文中出现的对称模式与非对称模式,若没有特殊说明,均指基模情况下的导制传播.图中“*”和“Δ”所示分别为水平波数0.04km-1时,重力波的部分导制传播下的对称模式和非对称模式.从图中还可以看出,对于导制传播的重力波,随着水平波数的增加,波频率也逐渐增大.
|
图 1 不同模式下重力波在温度波导中传播时的色散关系 实线和点线分别代表完全导制情况下的对称模式和非对称模式;虚线和点划线分别代表部分导制情况下的对称模式和非对称模式. Fig. 1 Dispersions of different modes for gravity waves propagating in a thermal duct Solid and dotted curves indicate fully symmetric and antisymmetric modes, respectively; dashed and dash dot curves indicate partially symmetric and antisymmetric modes, respectively. |
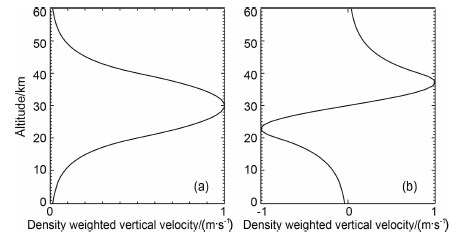
图 2为重力波部分导制传播时,对称与非对称模式下密度加权垂直风扰动的特征函数.从图中可以看出,重力波的特征函数分别关于波导中心高度对称和非对称,重力波部分导制传播时,波导边界处特征函数的值并不为零,这就可能引起波导内重力波能量在垂直方向上的泄漏,随着远离波导中心高度,扰动的振幅指数下降趋近于零.垂直方向上,对称模式下的特征函数在波导区域内存在约半个波结构,非对称模式下的特征函数存在约一个波结构.
|
图 2 重力波在温度波导中部分导制传播时密度加权垂直风的特征函数 (a)对称模式;(b)非对称模式. Fig. 2 Eigenfunctions of the density weighted vertical velocity ŵ for gravity waves propagating in a partial thermal duct (a) Symmetric mode; (b) Antisymmetric mode. |
图 3为对称与非对称模式下,重力波在该温度波导部分导制传播时频率和水平群速度随水平波数的变化.波导中重力波的频率介于N1和N0之间,并随着水平波数的增加而逐渐增加;重力波的水平群速度随着水平波数的增加而逐渐减小,在水平波数较小的区域,水平群速度随波数的增加下降得更快.在水平波长一致的情况下,非对称模式下的重力波和对称模式下的相比较,频率要略低,而水平群速度则比较大.
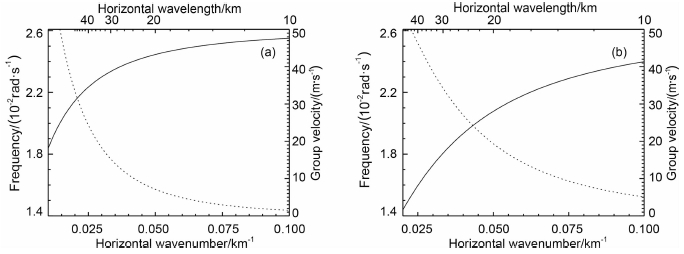
|
图 3 重力波在温度波导中传播时频率(实线)和水平群速度(点线)随水平波数的变化,其中N1=1.23×10-2rad/s,N0=2.61×10-2rad/s,h=10km (a)为对称模式;(b)为非对称模式. Fig. 3 Frequency (solid curve) and horizontal group velocity (dotted curve) as a function of horizontal wavenumber obtained from numerical solutions for the pure thermal duct, in which N1=1.23×10-2rad/s, N0=2.61×10-2 rad/sand h=10km (a) Symmetric mode; (b) Antisymmetric mode. |
对于二维可压大气,忽略大气黏性和地球自转效应,大气运动控制方程可写为如下形式:

|
(16) |
其中,x和z分别是水平和垂直方向坐标;u和w分别是水平和垂直风速;ρ、P和T分别是密度、压强和温度;R为普适气体常数(R=286.98J·kg-1· K-1);cv为定容比热(cv=781J·kg-1·K-1);g为重力加速度常数(g=9.80225m·s-2).
本文采用全非线性的FICE格式对二维无黏可压缩大气的控制方程进行数值模拟.FICE格式曾经成功地用于重力波的非线性传播研究[22, 23].具体的算法和网格选取参见文献[22].在本文的算例中,水平和垂直方向上分别选取周期边界条件和近特征线边界条件;水平与垂直计算区域分别为0~800km和5~75km,水平与垂直步长分别为2km和0.5km.
假设背景大气水平均匀分层并且满足流体静力学平衡条件,背景风速为零.温度波导模型方程(1)中,背景大气的浮力频率在界面z=z0±h处不连续,在数值模拟时,我们可以对浮力频率的分布做平滑近似[19],令
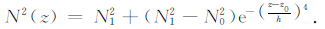
|
(17) |
温度波导模型的参数与2.3节模型分析时选取的温度波导参数一致,即N1=1.23×10-2rad/s,N0=2.61×10-2rad/s,z0=30km,h=10km.下边界处温度选取Tc=270K,由浮力频率的分布和静力学平衡条件就可计算出背景大气相应的温度分布和密度分布.
初始时刻,假定在下边界zc=5km处存在着垂直风强迫,时空分布形式为

|
其中σx=λx,xc=120km,w0=2m·s-1,T为强迫扰动的周期,λx为水平波长.扰动在下边界处形成以xc为中心,半宽σx的高斯形包络,在前4T时刻持续存在,相速在水平方向为正向传播.上述垂直风强迫如果在等温大气中,会产生一个中心频率ω=2π/T,水平波数为kx=2πλx的重力波包.
本文选取了初始扰动参数不同的两个例子进行数值模拟.两个例子中,初始扰动的频率与水平波数落在图 1所示“*”和“Δ”位置,分别对应于重力波部分导制情况下的对称模式与非对称模式.例1中初始扰动的水平波数为0.04 km-1,频率为0.0239rad/s,对应的水平波长为25km,周期为262.9s;例2中水平波数为0.04km-1,频率为0.0195rad/s,对应的水平波长为25km,周期为322.2s.
3.2 垂直风扰动图 4为例1中不同时刻密度加权的垂直风扰动ŵ=(ρ0/ρs)-1/2w′,其中ρs为下边界处背景大气密度,图中虚线代表垂直风扰动小于零,等值线的间隔为0.01m·s-1.背景大气温度波导中心高度为30km,半宽为10km,从图 4中可以看到,由下边界强迫引起的扰动在第10min时就开始进入波导区域,垂直风扰动达到约50km的高度.在第40 min时,下边界处扰动能量已经全部进入了波导区域,在数值模拟的时间内,重力波在垂直方向上始终被限制在10~50km的高度范围内,而且波包结构清晰,由此可认定此时的重力波发生了良好的导制传播.随着重力波在水平方向上向右的传播,波包水平扰动区域逐渐变大,波结构略有变化.第40 min时的波结构在波导区域内没有节点(ŵ=0),波结构大致关于波导中心高度z0=30km对称.第100min时,在波包的前列出现了一些垂直尺度较小的波结构,这些波结构在约30km高度附近存在着波节点.重力波在导制传播时,垂直风扰动的振幅逐渐减小.第40min时,波导区域内ŵ的最大值约为0.14m·s-1,而到了第190min时,波包向右传播了很长一段距离,ŵ的最大值减小到约为0.07m·s-1,此时400~500km区域内波结构ŵ的最大值约为0.02m·s-1.
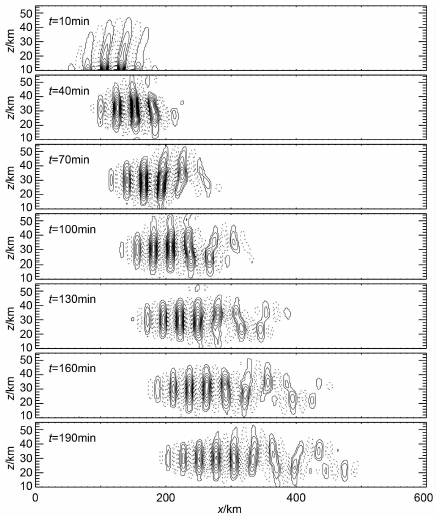
|
图 4 例1中波导区域内不同时刻垂直风扰动ŵ的分布 虚线表示ŵ<0,第10min时等值线间隔为0.04m·s-1,其余时刻等值线间隔为0.01m·s-1,实线的最小值和虚线的最大值分别为±0.005m·s-1. Fig. 4 Distributions of vertical wind disturbance ŵ at different times Dotted lines indicate ŵ < 0, contour intervals are 0.01m·s-1, except 0.04m·s-1at the 10th min, and the minimum solid contour and maximum dotted contour are±0.005m·s-1 respectively. |
图 5与图 4相似,只是为例2中的垂直风扰动分布.从图中可以看出下边界的扰动进入波导区域被俘获后,波包结构在垂直方向上也被限制在约10~50km的区域.图 5中波导区域内的波包结构随时间的变化更明显,第40 min时,波导区域的重力波大致关于波导中心高度对称,在约30km高度处存在着波节点,而在第100min时,波列已经很明显地形成了两组完全不一样的波结构.其中波前列的波结构在垂直方向上约30km有一个节点,关于波导中心高度非对称;波尾的波结构在波导区域没有波节点,关于波导中心高度对称.随着重力波在波导内的传播,对称结构与非对称结构的波包进一步地分离.图 5中重力波的垂直风扰动振幅也随着波的传播逐渐减小,第40 min时,波导区域内对称结构ŵ的最大值约为0.17m·s-1,而第190min时,非对称结构ŵ的最大值减小到约为0.09 m·s-1,对称结构重力波的振幅略小,约为0.04m·s-1.

|
图 5 与图 4相同,只是模拟例2中的情况 第10min时等值线间隔为6.0×10-2 m·s-1,其余时刻等值线间隔为1.5×10-2 m·s-1. Fig. 5 As in Fig. 4, but under the conditions of case2 Contour intervals are 1.5×10-2 m·s-1, except 6.0×10-2 m·s-1 at 10th min. |
结合图 2中垂直风扰动的特征函数的形式可知,模拟过程中波导区域内对称与非对称结构的重力波包分别对应着重力波导制传播时的对称模式与非对称模式.例1中,对称结构的重力波包占据着主导地位,而例2的传播过程中重力波的对称结构和非对称结构都比较明显,然而非对称结构重力波的振幅要较大.用最大熵谱法对波导范围内的各高度上的垂直风扰动做频谱分析,然后进行平均可以求出温度波导内重力波的水平波长.两个例子中频谱分析得到的水平波长均约为25km,与初始时刻下边界扰动的水平波长非常一致,可见在进入温度波导的过程中,水平波长基本无变化.
3.3 重力波频率在水平方向上固定位置处,每间隔2 min记录一次垂直风扰动在波导区域内的垂直剖面分布.用时间滑动窗对垂直风扰动随时间、高度的分布加窗后再进行二维FFT处理,然后每一时刻在相空间内对频率相同的谱分量进行积分,就可得到总的谱能量随频率、时间的分布.本文所采用滑动窗的宽度为30min,滑动间隔为2min.
图 6a和图 6b分别为例1和例2中水平方向不同位置处,重力波垂直风扰动ŵ的频率谱随时间的变化.从图 6a可以看出,重力波在经过温度波导中水平方向上不同位置时均存在着相同的两个频率成分,分别为2.27×10-2rad/s和1.75×10-2rad/s.两个谱分量的强度峰值并不是在同一时间抵达水平方向上固定位置处,频率较小的谱分量峰值抵达的时间要略早.而图 4中垂直风扰动的分布显示,波导区域的波列形成了非对称与对称形式的两个波结构,且非对称波结构的水平行进速度较快,因此可知频谱分析中出现的两个频率分量分别对应着导制传播情况下对称结构与非对称结构的重力波包,对称结构重力波包的频率要比非对称结构下的频率大,这也与模式分析理论预言的结果相吻合.例1中水平方向150、200、300km处对称结构重力波的垂直风频谱强度峰值分别为6.35×10-2、4.71×10-2、3.00×10-2(m·s-1)/cycle,非对称结构重力波的频谱强度峰值分别为2.24×10-2、1.76×10-2、1.57× 10-2(m·s-1)/cycle.对称结构下的谱强度峰值要远大于非对称结构下的谱强度峰值,对称形式的谱成分在例1中占主导地位.两种模式下的频谱强度均随着波在水平方向上的传播而减小.
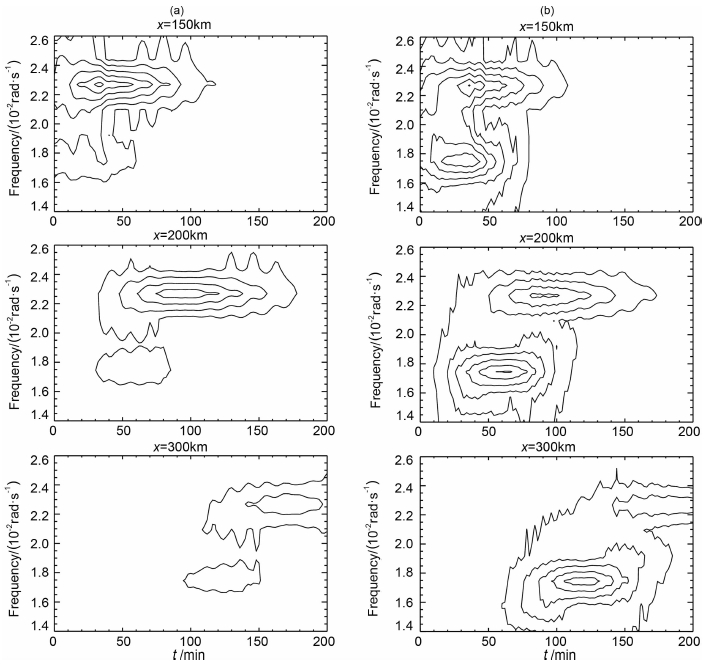
|
图 6 水平方向不同位置处,重力波频率谱随时间的变化 其中等值线的间隔为0.01(m·s-1)/cycle,等值线最小值为0.01(m·s-1)/cycle.(a)和(b)分别为例1和例2中的情形. Fig. 6 Frequency spectra of ducted gravity waves vs. time at fixed horizontal positions Contour intervals are 0.01 (m·s-1)/cycle, the minimum contour are 0.01 (m·s-1)/cycle. (a) and (b) stand for case1 and case 2, respectively. |
从图 6b可以看出,例2中重力波的频率也分别为2.27×10-2rad/s和1.75×10-2rad/s的谱分量,与例1中的两个频率成分相同.水平方向150、200、300km处重力波对称结构的频谱强度峰值分别为6.09×10-2、4.25×10-2、2.91×10-2(m·s-1)/ cycle,非对称结构重力波的频谱强度峰值分别为6.90×10-2、6.11×10-2、5.62×10-2(m·s-1)/ cycle.经过相同的水平位置时,非对称结构重力波包的谱强度峰值均大于对称形式下的谱强度峰值,由此可见例2中非对称形式重力波的谱成分略强.两种波结构重力波的频谱强度均随着波在水平方向上的传播而减小,本文的两个例子中,非对称模式波的频谱强度衰减得较慢.
4 讨论 4.1 传播模式讨论重力波完全导制传播时,会在波导的上下边界处出现波节点,能量会被完全局限在波导区域内.在模拟的两个例子中,重力波在波导上下边界处垂直风扰动值并不为0,而且随着重力波在波导区域内的水平传播,垂直风扰动的谱强度随之下降,因此重力波的总能量在波导区域内也有一定的泄漏.由此可以判断波导内的重力波为部分导制传播.
数值模拟中导制传播重力波的水平波长与初始扰动的水平波长非常一致,然而频率和初始扰动频率相比较却有着较大的差异.数值模拟的两个例子里,波导中均出现两个独立的重力波包结构,虽然初始扰动的频率很不相同,频谱分析却发现两个例子中出现的波频率完全一致.模拟的结果表明该波导中重力波结构的频率成分完全由背景大气波导结构和初始扰动的水平波数决定,与初始扰动的频率无关,这也是本文非常重要的计算结果.
模式分析显示,在特定的温度波导中,只有重力波的水平波长和频率满足一定的色散关系时才能形成导制传播.然而数值模拟的例子表明,在初始扰动的频率、水平波数与完全导制情况下的重力波色散关系差距较大的情况下,波导内的重力波在一段时间的传播后,由于行进速度的不一致,也分离成了分别以对称结构与非对称结构独立传播的两个波包.数值模拟的两个例子中非对称结构的重力波包行进得较快,这也与模式理论分析所得到的结论相一致,即非对称模式重力波水平群速度较大.
重力波在温度波导中导制传播时,频谱峰值随时间逐渐减小,而波的频率在图 6中并不发生改变.根据重力波谱强度峰值所抵达不同水平位置时的时间可以估算出重力波导制传播时的水平群速度.由图 6a可知,在例1中水平方向上200km处,对称模式传播的重力波频率分量在约100 min时达到峰值,水平方向上150km处,约30 min时达到峰值,由此可计算出水平群速度约为11.9m·s-1(由图 4可知在例1模拟计算的时间内,重力波对称结构波列中心尚未完全到达300km);图 6b中水平方向上200km处,非对称模式传播的重力波频率分量在约60min时达到峰值,水平方向上300km处,约120min时达到峰值,由此可计算出水平群速度约为27.8m·s-1.模拟得到的水平群速度与图 3中波导模型所预测的水平波长为25km的重力波在两种传播模式下的水平群速度11.0m·s-1和27.0m·s-1非常接近.
不同频率的初始扰动均能在温度波导中激发出以对称模式与非对称模式导制传播的重力波,然而两种模式下重力波的频谱分布却与初始扰动的频率-水平波数分布有关,初始扰动在图 1所示水平波数-频率空间中越接近于某种完全导制模式的色散关系曲线时,温度波导中被激发出来的以该种模式部分导制传播的重力波的频谱成分越强.结合图 1中导制传播的色散曲线可知,例1中重力波在波导区域内的相位变化Δφ略小于以对称模式完全导制传播所需要的相位条件π,模拟的结果显示波导中主要为对称结构的重力波包,非对称结构波包的强度非常小.而例2中,总相位变化介于π~2π间,而在模拟的实例里,对称与非对称两种模式的重力波都能在波导区域内看到,其中非对称模式重力波的频谱强度稍大.
4.2 对称模式与观测Tayler等[24]于1995年在Haleakala Crater观测到了一次不寻常的波事件,当波扰动进入气辉层时引起了OH层和OI层气辉强度的突变,两个气辉层扰动的相位恰好相差180°.此后对于不同气辉层间扰动的这种反相结构所给出的解释,多与重力波在温度波导中的活动相关.Munasinghe等[20]通过全波解的求解分析认为,这种现象是由重力波在中层大气温度波导中的完全导制传播引起的,Snively等[25]结合光化学反应的分析也证明了重力波在温度波导中传播时,波在垂直方向上的动力学结构可以引起不同气辉层间的180°相位差异.气辉成像仪观测到的扰动常用来研究重力波的导制传播,然而这样的反相结构只与重力波的非对称导制传播结构有关.
对于以对称模式导制传播的重力波,根据前文特征函数的分析可知其垂直波长远大于温度波导的厚度,无法引起不同层间扰动180°相位差异的结构.重力波在以对称模式传播时,垂直方向上只存在着约半个波结构,这也使人们在利用MF雷达、激光雷达等设备的观测数据进行分析时,难以提取出此类模式下的重力波.Fritts等[2]曾指出在估计大气中重力波的动量流通量以及考虑重力波参量化在大尺度环流模型中的效应时,要考虑到重力波的导制传播事件.由于对称结构的重力波包的导制传播事件难以从观测数据中提取出来,在估算重力波在大气中的动量流通量和能量流通量时应对其给予更多的关注.
对于气辉成像仪所观测到这类现象,还存在着另外一种解释,Dewan和Picard[26, 27]首次讨论了中层大气中的Bore模型,认为气辉成像仪观测到的这种反相结构应该归于中层大气中的Bore事件. Seyler[19]用模拟结果说明,重力波在波导内传播非线性进一步增强时会形成数个独立的孤立波,这一系列孤立波的组合即为观测到的Bore结构.然而讨论所涉及到的这些模型都是基于重力波在温度波导中的非对称模式,没有考虑到重力波的对称模式. Smith等人[28~30]也相继报道了气辉成像仪观测到的Bore事件,在确认Bore事件时,不同气辉层间的反相结构被认为是一个很重要的判据.如果对称形式的导制传播的重力波也能形成Bore事件,这样的Bore也不会出现引起两个气辉层间扰动的恰好反相,那么中层大气中的Bore事件存在数目将有可能大大超过我们根据观测到的例子所作出的估计.
5 结论重力波在大气中传播时,背景温度梯度的变化会影响到重力波的传播特性,波导的存在对于重力波在大气中传播时的谱结构演变有着很重要的意义.本文给出了更合理的重力波在中层大气温度波导中的传播模型,详细讨论了重力波的部分导制传播模式,得到了重力波在对称模式与非对称模式下的特征模式以及相应的解析形式的色散方程,并通过离散的求解获得了重力波在具体波导模型中的色散关系.
本文还利用全非线性的二维FICE格式对重力波在温度波导中的传播进行了数值模拟,模拟的结果成功地展现了重力波的对称与非对称导制传播.通过模拟结果的分析,还讨论了中层大气温度波导对于低层扰动的响应的全过程.
下边界的扰动能量在向上传播进入波导区域后,会在波导内形成以对称与非对称形式导制传播的两种重力波包结构,由于两者的行进速度不一致,最终会引起两种波结构的分离,其中非对称结构波包的行进速度更快一些.数值模拟得到的对称与非对称重力波波包结构在水平方向上的群速度,与线性模式分析所预测的水平群速度非常接近.
波导中重力波的水平波长与初始扰动的水平波长相同,而波导内以对称和非对称导制传播的重力波频率与初始扰动频率无关,这表明在已知的温度波导结构中,水平波数才是确定重力波传播特性的决定因素.同时,初始扰动的水平波数-频率分布在相空间越接近重力波完全导制传播某种模式色散关系曲线时,温度波导中以该种模式部分导制传播的重力波频谱分量越强.
| [1] | Fritts D C. Gravity wave saturation in the middle atmosphere:a review of theory and observations. Rev.Geophys. , 1984, 23(3): 275-307. |
| [2] | Fritts D C, Alexander M J. Gravity wave dynamics and effects in the middle atmosphere. Rev.Geophys. , 2003, 41(1): RG1003. DOI:10.1029/2001RG000106 |
| [3] | Alexander M J, Richter J H, Sutherland B R. Generation and trapping of gravity waves from convection with comparison to parameterization. J.Atmos.Sci. , 2006, 63(11): 2963-2977. DOI:10.1175/JAS3792.1 |
| [4] | Chimonas G, Hines C O. Doppler ducting of atmospheric gravity waves. J.Geophys.Res. , 1986, 91(D1): 1219-1230. DOI:10.1029/JD091iD01p01219 |
| [5] | Wang D Y, Tuan T F. Brunt-Doppler dueting of small-period gravity waves. J.Geophys.Res. , 1988, 93(A9): 9916-9926. DOI:10.1029/JA093iA09p09916 |
| [6] | Fritts D C, Yuan Li. An analysis of gravity wave ducting in the atmosphere:Eckart's resonances in thermal and Doppler ducts. J.Geoph.ys.Res. , 1989, 94(D15): 18455-18466. DOI:10.1029/JD094iD15p18455 |
| [7] | Fritts D C, Williams B P, She C Y, et al. Observations of extreme temperature and wind gradients near the summer mesopause during the MaCWAVE/MIDAS rocket campaign. Geophys.Res.Lett. , 2004, 31(24). DOI:10.1029/2003GL019389 |
| [8] | Taylor M J, Gu Y Y, Tao X, et al. An investigation of intrinsic gravity wave signatures using coordinated lidar and nightglow image measurements. Geophys.Res.Lett. , 1995, 22(20): 2853-2856. DOI:10.1029/95GL02949 |
| [9] | Isler J R, Taylor M J, Fritts D C. Observational evidence of wave ducting and evanescence in the mesosphere. J.Geophys.Res. , 1997, 102(D22): 26301-26313. DOI:10.1029/97JD01783 |
| [10] | Walterscheid R L, Hecht J H, Vincent R A, et al. Analysis and interpretation of airglow and radar observations of quasimonochromatic gravity waves in the upper mesosphere and lower thermosphere over Adelaide Australia (35°S, 138°E). J.Atmos.Sol.Terr.Phys. , 1999, 61(6): 461-478. DOI:10.1016/S1364-6826(99)00002-4 |
| [11] | Hecht J H, Walterscheid R L, Hickey M P, et al. Climatology and modeling of quasi-monochromatic atmospheric gravity waves observed over Urbana Illinois. J.Geophys.Res. , 2001, 106(D6): 5181-5195. DOI:10.1029/2000JD900722 |
| [12] | Waherscheid R L, Schubert G, Brinkman D G. Small-scale gravity waves in the upper mesosphere and lower atmosphere generated by deep tropical convection. J.Geophys.Res. , 2001, 106(1323): 31825-31832. |
| [13] | 李俊, 张绍东, 易帆. 重力波包在中层大气温度波导中传播的数值模拟. 地球物理学报 , 2007, 50(4): 1030–1039. Li J, Zhang S D, Yi F. A numerical simulation on gravity waves propagation in mesospheric thermal duct. Chinese J.Geophys. (in Chinese) , 2007, 50(4): 1030-1039. |
| [14] | Snively J B, Pasko V P. Breaking of thunderstorm-generated gravity waves as source of short period ducted waves at mesopause altitudes. Geophys.Res.Lett. , 2003, 30(24). DOI:10.1029/2003GL018436 |
| [15] | Meriwether J W, Gerrad A J. Mesosphere inversion layers and stratosphere temperature enhancements. Rev.Geophys. , 2004, 42(3): RG3003. DOI:10.1029/2003RG000133 |
| [16] | Dao P D, Farley R, Tao X, et al. Lidar observations of the temperature profile between 25 and 103 kin:evidence of tidal perturbation. Geophys.Res.Lett. , 1995, 22(20): 2825-2828. DOI:10.1029/95GL02950 |
| [17] | Tuan T F, Tadic D. A dispersion formula for analyzing modal interference' among guided and free gravity wave modes and other phenomena in a realistic atmosphere. J.Geophys.Res. , 1982, 87(A3): 1648-1668. DOI:10.1029/JA087iA03p01648 |
| [18] | Nappo C J. An Introduction to Atmospheric Gravity Waves. California: Academic Press, 2002 . |
| [19] | Seyler C E. Internal waves and undular bores in mesospheric inversion layers. J.Geophys.Res. , 2005, 110(D9). DOI:10.1029/2004JD004685 |
| [20] | Munasinghe G, Hur H, Huang T Y, et al. Application of the dispersion formula to long-and short-period gravity waves:comparisons with ALOHA-93 data and an analytical model. J.Geophys.Res. , 1998, 103(D6): 6467-6481. DOI:10.1029/97JD02850 |
| [21] | Hut H.Fully guided gravity waves at short-periods and gravity wave-critical layer interaction[Ph.D.thesis].Cincinnati:Cincinnati Univ., 1998 |
| [22] | Zhang S D, Yi F. A numerical study of nonlinear propagation of a gravity-wave packet in compressible atmosphere. J.Geophys.Res. , 1999, 104(D6): 14261-14270. |
| [23] | Zhang S D, Yi F. A numerical study of propagation characteristics of gravity wave packets propagating in a dissipative atmosphere. J.Geophys.Res. , 2002, 107(D14). DOI:10.1029/20011DO00864 |
| [24] | Tayler M J, Turnbull D N, Lowe R P. Spectrometric and imaging measurements of a spectacular gravity wave event observed during the ALOHA-93 campaign. Geophys.Res.Lett. , 1995, 22(20): 2848-2852. |
| [25] | Snively J B, Pasko V P. Antiphase OH and Of airflow emissions induced by a short-period ducted gravity wave. Geophys.Res.Left. , 2005, 32(8): L08808. DOI:10.1029/2004GL022221 |
| [26] | Dewan E M, Picard R H. Mesospheric bores. J.Geophys.Res. , 1998, 103(D6): 6295-6305. DOI:10.1029/97JD02498 |
| [27] | Dewan E M, Picard R H. On the origin of mesospheric bores. J.Geophys.Res. , 2001, 106(D3): 2921-2927. DOI:10.1029/2000JD900697 |
| [28] | Smith S M, Taylor M J, Swenson G R, et al. A multidiagnostic investigationof mesospheric bore phenomenon. J.Geophys.Res. , 2003, 108(A2). DOI:10.1029/2002JA009500 |
| [29] | Smith S M, Friedman J, Raizada S, et al. Evidence of mesospheric bore formation from a breaking gravity wave events:simultaneous imaging and lidar measurements. J.Atmos.Sol.Terr.Phys. , 2005, 67(4): 345-356. DOI:10.1016/j.jastp.2004.11.008 |
| [30] | Brown L B, Gerrard A J, Meriwether J W, et al. All-sky imaging observations of mesospheric fronts in OI 557.7 nm and broadband OH airglow emissions., analysis of frontal structure, atmospheric background conditions, and potential sourcing mechanisms. J.Geophys.Res. , 2004, 109(D19). DOI:10.1029/2003JD004223 |
 2010, Vol. 53
2010, Vol. 53

