2. NARI Technology Co. Ltd., Nanjing 211106, China;
3. State Key Laboratory of Smart Grid Protection and Control, Nanjing 211106, China;
4. Anhui Electric Power Research Institute, Hefei 230061, China;
5. Southeast University, Nanjing 210096, China
Electromechanical transient simulation of power system, an effective approach to analyze the stability of power system, is one of the significant simulation tools to the power system planning, dispatching and scientific research [1, 2]. Nowadays, there are two main methods towards electromechanical transient simulation, namely time simulation [3] and direct method [4]. Time simulation is the most common approach to the execution of electromechanical transient simulation of power system, but serial electromechanical transient simulation algorithm often consumes a lot of time and fails real-time requirements. The analysis of the transient process of power grid depends on detailed modeling and simulation. Fine-grained parallel computing devices such as Graphics Processing Unit (GPU) can significantly improve the transient simulation efficiency of power grid [5-7].
State-of-the-art GPU, with Single Instruction Multiple Threads (SIMT) architecture, has superior performances on float-pointing calculation and memory bandwidth. Therefore, GPU offers an alternative and potentially superior solution for batch-ETTS problem.
When referring to existing researches to accelerate ETTS, two different technical frameworks can be proposed: Space Paralleled Algorithm and Time Paralleled Algorithm [8]. The principle of space paralleled algorithm is to divide large power systems into several subsystems and calculate [9, 10]. Bordered block diagonal form (BBDF) [11, 12], which is implemented on the cluster processing LU factorization. Time paralleled algorithm was first introduced into power system transient simulation by Alvarado [13]. Its principle is to solve the difference equations of differential equations on multiple integral time steps simultaneously with the network equations. Two kinds of iterative methods, namely Gauss-Jacobi-Newtown (G-J) [14] and Gauss-Seidel-Newtown (G-S) [15, 16], are commonly used today. But they are both hard to be implemented as program. In this regard, we proposed a novel parallel algorithm for batch-ETTS on GPUs.
The paper is organized as follows. Section 2 presents the principles and process of implicit integration alternating solution method [17]. In Sect. 3, the proposed GPU-accelerated batch up-looking LU factorization and batch dynamic element injection current solver are presented. Section 4 proposes a novel GPU-accelerated batch-ETTS algorithm. Three cases are tested and compared in Sect. 5. Finally, Sect. 6 makes the conclusion of this paper.
2 Algorithm Principles 2.1 The Principles of IIASMImplicit integration alternative solution has both the good numerical stability of implicit integral and the flexibility of explicit integral. Figure 1 shows the workflow of this algorithm.
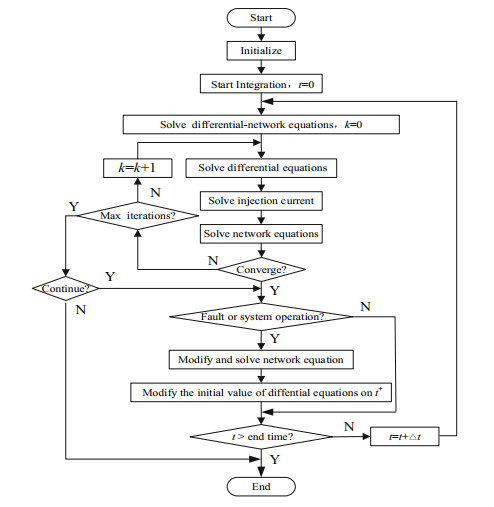
|
Fig.1 The basic workflow of implicit alternative solution |
The mathematical model of dynamic elements are expressed as
| $ {\dot X_d} = {f_d}\left( {{X_d}, {V_d}} \right) $ | (1) |
| $ {I_d} = {g_d}\left( {{X_d}, {V_d}} \right) $ | (2) |
where Xd is the state vector of dynamic elements, Id is the injection current of dynamic element, Vd is the node voltage of dynamic component.
Differential-algebraic equation are expressed as
| $ \dot X = f\left( {X, V} \right) $ | (3) |
| $ I\left( {X, V} \right) = {Y_N}V $ | (4) |
where X is system state vector, V is the node voltage vector, I is the node injection current vector, YN is the node admittance matrix.
Using the state vector Xn and the node voltage Vn of time tn, the detailed principle of solving Xn+1 and Vn+1 of time tn+1 = tn + Δt is
From (3) and (4) we can get the following non-linear equations.
| $ {X_{n + 1}} = {X_n} + \frac{{\Delta t}}{2}\left[ {f\left( {{X_n}, {V_n}} \right) + f\left( {{X_{n + 1}}, {V_n}} \right)} \right] $ | (5) |
| $ I\left( {{X_{n + 1}}, {V_{n + 1}}} \right) = {Y_N}{V_{n + 1}} $ | (6) |
Then the iterative solution is used to solve non-linear equations. LU factorization is executed on the coefficient matrix before iteration begins. We can simply use factorized table to do backward or forward substitution.
2.2 The Principles of Dynamic Elements SolverThe dynamic component on the power system network only affects the injection current of the node where it is located. Moreover, this current is only related to the state variables of the dynamic element and the node voltage, which does not depend on other dynamic elements. This is the key to decoupling implicit integration alternative solution and it is the main reason why we can use GPU to parallelize and boost this problem.
The classical second-order model of the synchronous generator is expressed as
| $ \left\{ \begin{array}{l} {T_J} = \frac{{d\omega }}{{dt}} = {T_m}- {\rm{Re}}\left( {\dot E'\mathop I\limits^ * }\right)- D\left( {\omega -1} \right) \\ \frac{{d\delta '}}{{dt}} = \omega - 1 \end{array} \right. $ | (7) |
| $ \dot U = \dot E' -\left( {{r_a} + {\rm{j}}{{\mathit{X'}}_\mathit{d}}} \right)\dot I $ | (8) |
where Re is real part calculation, and * means conjugation,
In the above classical second-order model, there are two state variables, namely ω and δ′. For the sake of simplicity, the first formula in Eq. 7 is abbreviated as
Step 1, solving the current
Step 2, solving the state vector:
| $ \omega _{n + 1}^{k + 1} = {\omega _n} + \frac{{\Delta t}}{2}\left[ {{f_d}\left( {{\omega _n}, {{\dot I}_n}} \right) + {f_d}\left( {\omega _{n + 1}^k, \dot I_{n + 1}^k} \right)} \right] $ | (9) |
| $ {\delta '}_{n + 1}^{k + 1} = {{\delta '}_n} + \frac{{\Delta t}}{2}\left[ {\left( {{\omega _n}- 1} \right){ + }\left( {\omega _{n + 1}^{k + 1} -1} \right)} \right] $ | (10) |
Step 3, solving the current
Step 4, replacing
Step 5, comparing whether the
In compliance with SIMT architecture, four general design criteria for GPU-based algorithms should be followed. Criterion 1: exploring parallelism fully to saturate the numerous computing cores on GPU. Criterion 2: fulfilling coalesced memory access to improve memory efficiency. Criterion 3: avoiding thread divergence of thread warp. Criterion 4: reducing data communication between CPU and GPU. In the workflow of IIASM, solving SLS and dynamic element injection current are the two most time-consuming parts, so the GPU-accelerated algorithms are elaborated according to the four design criteria below.
3.1 GPU-Accelerated Single SLS LU FactorizationAs shown in Table 1, in order to accelerate the up-looking LU factorization, multiple GPU threads are used to solve the executable rows concurrently. This kind of parallelism is determined by the sparse structure of L. As is shown in Fig. 2, the number of rows which can be parallelized in each layer declines dramatically as the number of layers increases. This phenomenon will be more notable in matrices with higher order (Tables 1, 2 and Fig. 2).
| Table 1 Hierarchical paralleled sparse up-looking LU factorization |
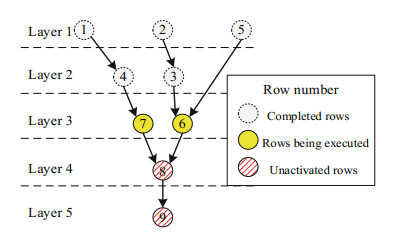
|
Fig.2 The dependence graph of a 9-order matrix |
| Table 2 Domino optimization based paralleled up-looking LU factorization |
In view of this phenomenon, Domino Algorithm in Table 2 is proposed. With Domino Algorithm, we can do part of the factorization operation ahead of time, other than waiting for all the dependencies to finish, thus increased the efficiency.
3.2 GPU-Accelerated Batch SLS LU FactorizationConsidering that batch electromechanical transient simulation contains a large number of sparse structures, a batch up-looking LU factorization algorithm is designed to realize a bunch of sparse matrices LU factorization. To be concrete, the principle is shown in Fig. 3. The principle of batch sparse matrices up-looking LU factorization mainly consists of the following points: (1) Unified sparse structure; (2) Task-level parallelism; (3) Memory merge access principle. And Batch LU factorization algorithm is given in Table 3.
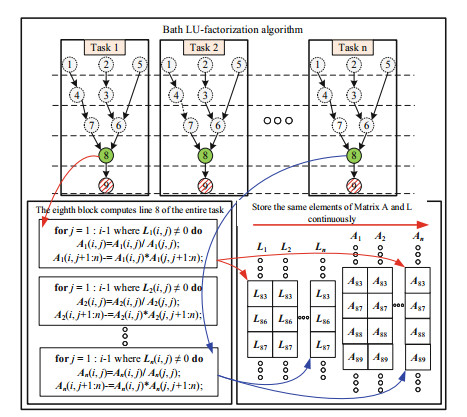
|
Fig.3 Batch LU factorization algorithm schematic diagram |
| Table 3 GPU-based batch LU factorization algorithm |
The principle of GPU-accelerated batch triangular equations solution is similar to the batch up-looking LU factorization Algorithm. A thread block is used to update the right vector of the same row of all trigonometric equations. The right vector is also stored in memory continuously.
3.3 GPU-Accelerated Batch Dynamic Element SolverThe injection current calculation process of each motor is the same, but the number of iterations is different. According to the principle above, tasks of solving injection current for dynamic elements in electromechanical transient simulation is packaged and solved in batch. The details are shown in Fig. 4.

|
Fig.4 Optimization design of batch dynamic element injection current solver |
4 Batch-ETTS Algorithm Based on IIASM
Based on the batch LU factorization and dynamic element injection current solver algorithm, a novel GPU-accelerated batch-ETTS algorithm for multiple scenarios is proposed in this section.
The framework of the proposed GPU-accelerated batch-ETTS algorithm is given in Fig. 5.
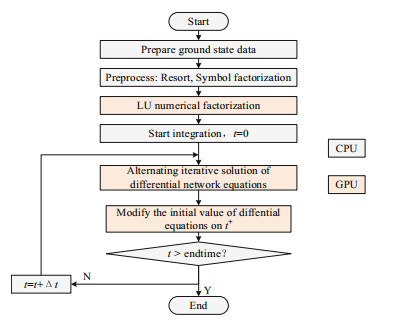
|
Fig.5 GPU-accelerated batch-ETTS algorithm for multiple scenarios |
5 Case Study and Performance Comparison 5.1 Case Study
The test platform is the server equipped with a NVIDIA Tesla K40 GPU and two 6-core Intel Xeon E5-2620 CPU. The operating system is CentOS 6.7 and the CUDA version is 8.0. The three cases are IEEE-118 bus test case, European 1354-bus system case and 9241-bus system case extracted from MATPOWER [18].
(1) Batch dynamic element injection current solver
The detail test information of case 3 with 1445 generators is presented in below. Table 4 illustrates that the time of single simulation quickly tends to saturation with the increase of batch number, and finally gradually tends to 0.014 ms.
| Table 4 Injection current of dynamic elements calculation in case 3 |
(2) Batch SLS solver
According to Table 5, when the batch number is under 256, time increases rather slowly with that becoming larger. When the batch scale is under 256, the band width only reach 39% of the theoretical peak. When that increases to over 512, the actual band width can keep stable at 190 GB/s, which reached a peak of 66% theory.
| Table 5 Band width of LU factorization and for/backward substitution in case 3 (GB/s) |
The overall performance of GPU accelerated batch sparse triangular equations with forward and backward substitution is similar to LU factorization in that with the increase of batch number.
5.2 Performance ComparisonCompared with KLU solution, batch LU factorization achieved very high speedup effect. As is shown in Table 6, average single solution of LU factorization is 200 times faster than the KLU serial solution. When the order of matrix is smaller, the GPU speedup is relatively better.
| Table 6 Performance of GPU-accelerated batch LU factorization (ms) |
6 Conclusion
In this paper, a batch SLS algorithm with task-level coarse-grained parallel mode and data-level fine-grained parallel mode is designed for simulation in multiple scenarios. Then, according to the parallelism of two layers, the algorithm of dynamic elements injection current is proposed. Finally, a batch transient simulation algorithm based on GPU acceleration is designed according to the principle of implicit integration alternative solution.
Case studies on Case 3 shows that, when the batch size is equal to 3072, the proposed batch LU factorization on NVIDIA Tesla K40 reaches its performance saturation point 0.29 ms per SLS and achieves 160 times speedup compared with KLU. By means of offloading the massive SLS and batch dynamic element injection current subtasks to GPU, the proposed batch-ETTS algorithm can limit the time in one alternate iteration of single ETTS within 0.5 ms for one system with over 10, 000 nodes.
| 1. |
Shu Y, Zhang W, Zhou X, et al (2017) Analysis and recommendations for the adaptability of China's power system security and stability relevant standards. CSEE J Power Energy Syst
3: 334-339. DOI:10.17775/CSEEJPES.2017.00650 (  0) 0) |
| 2. |
Zhao L, Guo Q, Qin Q, et al (2008) Analysis of stability characteristics of UHV synchronous power grid. Proc CSEE
34: 47-51. (  0) 0) |
| 3. |
Yu Y, Chen L (1988) Power system safety and stability, 1st edn. Science Press, Beijing (1988)
(  0) 0) |
| 4. |
Shao H (1991) Direct method analysis of power system stability analysis. 1st edn.
Water Resources and Electric Power Press, Beijing.
(  0) 0) |
| 5. |
Chen Y, Song Y, Huang S, et al (2017) GPU-based techniques of parallel electromagnetic transient simulation for large-scale distribution network. Autom Electr Power Syst
19: 82-88. (  0) 0) |
| 6. |
Wang M, Chen Y, Huang S, et al (2018) Power flow computation method for large-scale ill-conditioned systems applied to CPU and GPU coordination architecture. Autom Electr Power Syst
10: 82-86. (  0) 0) |
| 7. |
Zhao J, Liu J, Li P, et al (2018) GPU based parallel algorithm oriented to exponential integration method for electromagnetic transient simulation. Autom Electr Power Syst
6: 113-119. (  0) 0) |
| 8. |
Xue W, Wu S, Wang X, et al (2002) Research progress on parallel algorithm for power system transient stability simulation. J Syst Simul
2: 177-182. (  0) 0) |
| 9. |
Xue W, Wu S, Wang X, et al (2003) Parallel simulation of large scale power system transient process based on cluster machine. Proc CSEE
8: 39-44. (  0) 0) |
| 10. |
Wu JQ, Bose A, Huang JA, et al (1995) Parallel implementation of power system transient stability analysis. IEEE Trans Power Syst
(3): 1226-1233. (  0) 0) |
| 11. |
Chan KW (2001) Parallel algorithms for direct solution of large sparse power system matrix equations. IEE Proc C: Gener Transm Distrib
6: 615-622. (  0) 0) |
| 12. |
Su X, Mao C, Lu J (2002) Parallel power flow calculation for diagonal block plus edge model. Power Syst Technol
(1): 22-25. (  0) 0) |
| 13. |
Alvarado FL (1979) Parallel solution of transient problems by trapezoidal integration. IEEE Trans Power Appar Syst 3: 1080-1090 GPU-Accelerated Batch Electromechanical Transient … 683
(  0) 0) |
| 14. |
Granelli GP, Montagna M, La Scala M, et al (1994) Relaxation-Newton methods for transient stability analysis on a vector/parallel computer. IEEE Trans Power Syst
2: 637-643. (  0) 0) |
| 15. |
La Scala M, Brucoli M, Torelli F, et al (1990) A Gauss-Jacobi-Block-Newton method for Parallel transient stability analysis (of power systems). IEEE Trans Power Syst
4: 1168-1177. (  0) 0) |
| 16. |
La Scala M, Sbrissai R, Torelli F (1991) A pipelined-in-time parallel algorithm for transient stability analysis. IEEE Trans Power Syst
2: 715-722. (  0) 0) |
| 17. |
Tang Y (1997) Power system stability calculation implicit integration. Power Syst Technol
2: 1-3. (  0) 0) |
| 18. |
Zimmerman RD, Murillo-Sánchez CE, Thomas RJ (2011) MATPOWER: steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans Power Syst
1: 12-19. (  0) 0) |
 2020 : 673-684 DOI: 10.1007/978-981-13-9783-7_55
2020 : 673-684 DOI: 10.1007/978-981-13-9783-7_55



