文章编号: 2096-3203(2024)06-0078-10 中图分类号: TM72
2. 西安交通大学(电工材料电气绝缘全国重点实验室), 陕西 西安 710049
分频输电系统(fractional frequency transmission system, FFTS)通过降低输电频率提高传输效率,缩短了交流输电线路的输电距离,提高了暂态稳定性,且保护可靠性高,无技术瓶颈,为海上风电送出提供了更好的选择[1-2]。AC/AC换流器是分频海上风电系统能够稳定运行的关键设备,其结构和控制方式的选择直接影响FFTS整体的性能[3]。目前主流研究的AC/AC换流器包括模块化多电平换流器(modular multilevel converter, MMC)[4]、六边形MMC[5]和模块化多电平矩阵式换流器(modular multilevel matrix converter,M3C)[6]。M3C将矩阵式交交变频器的拓扑结构和模块化多电平技术相结合,与MMC相比,M3C具有低谐波、高功率因数和快速响应等优点[7],在分频输电领域有良好的发展前景。
目前M3C常用的控制方法为矢量控制法、双αβ坐标变换法和双dq坐标变换法等[8]。文献[9-10]提出了M3C的空间矢量控制策略,在高压大功率系统中,M3C级联的子模块数量较多,采用空间矢量法会大大增加控制系统的复杂性;文献[11-16]采用桥臂电流直接反馈,所提出的控制策略可以免于复杂的坐标变换,实现电容电压的稳定运行,但桥臂电流直接反馈控制为交流量控制,不易保证控制器的稳态无差特性和动态性能;为了克服直接电流反馈控制的缺陷,目前M3C通常使用间接电流反馈控制,即对桥臂电流进行解耦,形成电压电流双闭环的级联控制方式[17-18];文献[19-20]采用双αβ坐标变换的解耦控制方法,简化了M3C数学模型,并且可以实现自由度的解耦控制,但在这种方式下物理意义不清晰,功率计算复杂;文献[21]首次提出了M3C双dq坐标变换的解耦控制策略,实现了输入频率与输出频率解耦控制;在该控制策略基础上,文献[22-23]提出了M3C在不同故障情况下的故障控制策略,实现了M3C故障情况低扰动穿越。
为了稳定电网频率,有学者提出在换流器控制方案中引入同步发电机的特性,从而达到提高电力系统惯性水平的目的,并称其为虚拟同步发电机或同步换流器[24-27]。目前虚拟同步技术主要聚焦于直流输电系统或新能源直流并网逆变器[28-33],对海上风电FFTS虚拟同步控制的分析和设计研究较少。
相较于直流系统,海上风电FFTS采用AC/AC换流器,其数学模型较为复杂,虚拟同步发电机特性的等效和引入较为困难;其次,换流器控制维度更多,控制器设计须考虑内外环控制器的衔接以及换流器两端控制策略的协调配合。因此文中以分频海上风电送出场景下M3C为核心,开展M3C虚拟同步发电机控制策略研究,为海上风电FFTS高压大容量交交变频器提供一种新的控制方案。
1 M3C系统与同步发电机系统对比 1.1 M3C系统与同步发电机系统结构参数对比如图 1所示,在分频海上输电系统中,风电机组、低频变压器和低频输电线路等M3C低频侧系统对应原动机M,为系统提供机械功率;虚拟同步发电机控制下的M3C对应传统旋转同步发电机SG;M3C所连工频系统对应发电机出口的交流电网。因此,M3C系统结构与同步发电机系统结构具有高度对应性和一致性。

|
图 1 M3C系统与同步发电机系统结构对应关系 Fig. 1 M3C system and synchronous generator system structure corresponding relationship |
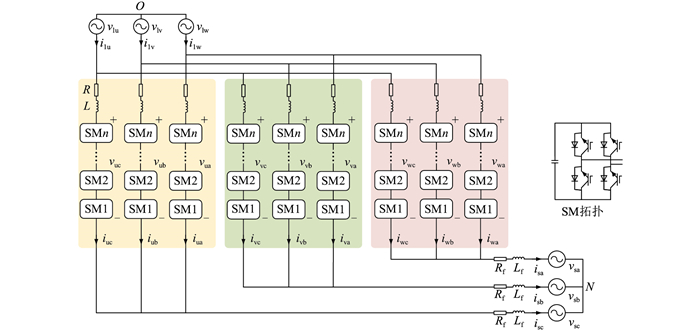
M3C拓扑如图 2所示,低频侧中性点用O表示,工频侧中性点用N表示。9个桥臂支路对称分布于低频交流系统和工频交流系统之间,每个桥臂由n个全桥子模块SM、电感L和等效电阻R组成,在正常运行时,根据系统功率与输入输出电压等级的需求,计算M3C桥臂所需级联子模块的个数,从而使得桥臂呈现相应的调制电压。图中,vsa、vsb、vsc为工频侧公共连接点(point of common, PCC)电压;vlu、vlv、vlw为低频侧端电压;i1u、i1v、i1w为低频侧输入电流;vui、vvi、vwi为i相子换流器的桥臂电压, i=a,b,c;iui、ivi、iwi为i相子换流器的桥臂电流;isa、isb、isc为工频侧输出电流;Rf+Lf为M3C到工频PCC处的连接阻抗。
|
图 2 M3C拓扑 Fig. 2 Topology of M3C |
输入侧和输出侧都可以看作3个星型连接的子换流器。文中以M3C低频侧流向工频侧为参考方向,以工频侧a相子换流器为例可得:
| $ \left\{\begin{array}{l} v_{\mathrm{sa}}=v_{\mathrm{lu}}-v_{\mathrm{ua}}-R i_{\mathrm{ua}}-L \frac{\mathrm{~d} i_{\mathrm{ua}}}{\mathrm{~d} t}-R_{\mathrm{f}} i_{\mathrm{sa}}-L_{\mathrm{f}} \frac{\mathrm{~d} i_{\mathrm{sa}}}{\mathrm{~d} t}-v_{O N} \\ v_{\mathrm{sa}}=v_{\mathrm{lv}}-v_{\mathrm{va}}-R i_{\mathrm{va}}-L \frac{\mathrm{~d} i_{\mathrm{va}}}{\mathrm{~d} t}-R_{\mathrm{f}} i_{\mathrm{sa}}-L_{\mathrm{f}} \frac{\mathrm{~d} i_{\mathrm{sa}}}{\mathrm{~d} t}-v_{O N} \\ v_{\mathrm{sa}}=v_{\mathrm{lw}}-v_{\mathrm{wa}}-R i_{\mathrm{wa}}-L \frac{\mathrm{~d} i_{\mathrm{wa}}}{\mathrm{~d} t}-R_{\mathrm{f}} i_{\mathrm{sa}}-L_{\mathrm{f}} \frac{\mathrm{~d} i_{\mathrm{sa}}}{\mathrm{~d} t}-v_{O N} \end{array}\right. $ | (1) |
式中:vON为工低频中性点间电压,在稳定运行情况下通常视为0。将式(1)中的三式相加并整理可以得到:
| $ \begin{gathered} v_{\mathrm{sa}}=-\left(R_{\mathrm{f}}+\frac{R}{3}\right) i_{\mathrm{sa}}-\left(L_{\mathrm{f}}+\frac{L}{3}\right) \frac{\mathrm{d} i_{\mathrm{sa}}}{\mathrm{~d} t}- \\ \frac{1}{3}\left(v_{\text {ua }}+v_{\mathrm{va}}+v_{\mathrm{wa}}\right) \end{gathered} $ | (2) |
esa、esb、esc分别为M3C工频侧桥臂a、b、c三相输出电压,满足:
| $ \left\{\begin{array}{l} e_{\mathrm{sa}}=-\frac{1}{3}\left(v_{\mathrm{ua}}+v_{\mathrm{va}}+v_{\mathrm{wa}}\right) \\ e_{\mathrm{sb}}=-\frac{1}{3}\left(v_{\mathrm{ub}}+v_{\mathrm{vb}}+v_{\mathrm{wb}}\right) \\ e_{\mathrm{sc}}=-\frac{1}{3}\left(v_{\mathrm{uc}}+v_{\mathrm{vc}}+v_{\mathrm{wc}}\right) \end{array}\right. $ | (3) |
根据式(2)和式(3)可得:
| $ \boldsymbol{v}_{\mathrm{s}}=-\left(R_{\mathrm{f}}+\frac{R}{3}\right) \boldsymbol{i}_{\mathrm{s}}-\left(L_{\mathrm{f}}+\frac{L}{3}\right) \frac{\mathrm{d} \boldsymbol{i}_{\mathrm{s}}}{\mathrm{~d} t}+\boldsymbol{e}_{\mathrm{s}} $ | (4) |
式中:vs=[vsa vsb vsc]T;is=[isa isb isc]T;es=[esa esb esc]T。
以模拟同步发电机惯量为主,考虑定子绕组存在电阻损耗,采用式(5)作为同步发电机定子电气方程模型[34]。
| $ \boldsymbol{u}_{\mathrm{abc}}=-R_{\mathrm{s}} \boldsymbol{i}_{\mathrm{abc}}-L_{\mathrm{s}} \frac{\mathrm{~d} \boldsymbol{i}_{\mathrm{abc}}}{\mathrm{~d} t}+\boldsymbol{e}_{\mathrm{abc}} $ | (5) |
式中:uabc为同步发电机定子绕组端电压;iabc为定子电流;eabc为同步发电机感应电动势;Rs、Ls分别为同步发电机定子电阻、电抗。
对比式(4)和式(5)可知,满足式(5)的传统同步发电机与M3C在系统内部参数上具有对应性:M3C等效电阻与同步发电机电枢电阻相对应,M3C等效电感与同步发电机内部电感相对应,M3C阀侧电压与同步发电机内电势相对应,风电机组和低频输电线路与原动机相对应。
1.2 基于虚拟直流电容的M3C系统与同步发电机系统运动方程对比假设能量在M3C内部9个桥臂之间完全平衡,桥臂虚拟直流电压Uce等于同一桥臂上所有子模块电压之和,即:
| $ U_{\mathrm{ce}}=n U_{\mathrm{sm}} $ | (6) |
式中:Usm为子模块电容电压。利用功率平衡原理可得:
| $ 9 n \times \frac{1}{2} C_{\mathrm{sm}} U_{\mathrm{sm}}^2=\frac{1}{2} C_{\mathrm{e}} U_{\mathrm{ce}}^2 $ | (7) |
式中:Csm为子模块电容;Ce为桥臂虚拟直流电容。
将式(6)代入式(7)可得:
| $ C_{\mathrm{e}}=\frac{9 C_{\mathrm{sm}}}{n} $ | (8) |
因此,M3C桥臂电容可以等效为图 3。图中,iC为电容电流;im为输入电流;ie为输出电流。

|
图 3 桥臂电容等效电路 Fig. 3 Bridge arm capacitance equivalent circuit |
M3C子模块电容的静态储能Ek和同步发电机转子的旋转动能Wk分别为:
| $ \left\{\begin{array}{l} E_{\mathrm{k}}=9 n \times \frac{1}{2} C_{\mathrm{sm}} U_{\mathrm{sm}}^2=4.5 n C_{\mathrm{sm}} U_{\mathrm{sm}}^2 \\ W_{\mathrm{k}}=\frac{1}{2} J \omega^2 \end{array}\right. $ | (9) |
式中:J为转动惯量;ω为转子机械角速度。
由式(9)可以看出,M3C子模块电容的静态储能Ek与同步发电机转子的旋转动能Wk相对应,子模块电容电压Usm与同步发电机转子机械角速度ω相对应。因此从机电暂态过程可以看出,M3C系统与同步发电机具有很高的对应性。
由图 3可以推出M3C桥臂电容满足:
| $ i_C=i_{\mathrm{m}}-i_{\mathrm{e}}=9 C_{\mathrm{sm}} \frac{\mathrm{~d} U_{\mathrm{sm}}}{\mathrm{~d} t} $ | (10) |
式(10)等式两侧同时乘以桥臂额定电压,正常运行时子模块额定电压为常量UsmN,可以得到:
| $ 9 n C_{\mathrm{sm}} U_{\mathrm{smN}} \frac{\mathrm{~d} U_{\mathrm{sm}}}{\mathrm{~d} t}=P_{\mathrm{m}}-P_{\mathrm{e}} $ | (11) |
式中:Pm为M3C输入功率;Pe为M3C输出功率。
不考虑阻尼绕组的情况下,同步发电机的转子运动方程为:
| $ J \frac{\mathrm{~d} \omega}{\mathrm{~d} t}=T_{\mathrm{m}}-T_{\mathrm{e}} $ | (12) |
式中:Tm为原动机机械转矩;Te为发电机电磁转矩。
式(12)两侧同时乘以额定角速度ω0得:
| $ J \omega_0 \frac{\mathrm{~d} \omega}{\mathrm{~d} t}=P_{\mathrm{m}}-P_{\mathrm{e}} $ | (13) |
比较式(11)和式(13)可知,M3C的子模块电容与同步发电机转子具有相同的动态模型。
综上所述,M3C系统与同步发电机系统在系统结构、系统参数和运动方程上具有极高的对应性和一致性,可以通过控制手段实现对M3C同步发电机特性的模拟。
2 M3C虚拟同步发电机控制系统的设计 2.1 有功控制器的设计将同步发电机转子运动方程引进虚拟同步发电机基本算法中,可以得到M3C的虚拟转子运动方程:
| $ \left\{\begin{array}{l} J_{\mathrm{c}} \frac{\mathrm{~d} \omega_{\mathrm{c}}}{\mathrm{~d} t}=T_{\mathrm{m}}-T_{\mathrm{e}}-D_{\mathrm{c}}\left(\omega_{\mathrm{c}}-\omega_{\mathrm{g}}\right) \\ \frac{\mathrm{d} \delta_{\mathrm{c}}}{\mathrm{~d} t}=\omega_{\mathrm{c}} \end{array}\right. $ | (14) |
其中:
| $ \left\{\begin{array}{l} T_{\mathrm{m}}=\frac{P_{\mathrm{m}}}{\omega_0} \\ T_{\mathrm{e}}=\frac{P_{\mathrm{e}}}{\omega_0} \end{array}\right. $ | (15) |
式中:Jc为换流器虚拟转子的转动惯量;ωc为换流器虚拟转子机械角速度;ωg为电网角速度,若同步电机的转子只有一对磁极,则在没有大规模负荷变动的电网中,电网角速度、额定角速度和转子机械角速度三者之间的误差极小,可以近似认为ωc≈ωg≈ω0;Dc为换流器虚拟阻尼系数;δc为转子的电角度。
Jc和Dc的引入可以使M3C对外表现出惯量和阻尼特性。与同步发电机不同的是,Jc和Dc不再受实物限制,可根据系统响应自行设定。当系统传输功率发生波动引起Pm与Pe不平衡时,由于转动惯量和阻尼系数的存在,交流频率发生缓慢变化,虚拟同步发电机控制可以暂时储存或释放子模块电容中的能量,参与系统频率调节。
在此基础上,为了使M3C参与电网的电压频率调节,虚拟同步发电机控制还需要模拟同步发电机的调速器系统和励磁系统。文中采用P-ω下垂特性来模拟同步发电机调速器控制特性。
| $ P_{\mathrm{ref}}-P_{\mathrm{m}}=D_{\mathrm{p}}\left(\omega_{\mathrm{c}}-\omega_0\right) $ | (16) |
式中:Pref为M3C输入功率的参考值;Dp为P-ω下垂系数。
在海上风电送出的典型场景下,M3C低频侧通过海底电缆连接风电机组,相当于低频侧连接弱电网,因此M3C低频侧应采用Vf控制以保证弱电网电压频率稳定运行。M3C工频侧控制要保证在无扰动时子模块电容电压稳定,因此将子模块电容电压控制回路引入虚拟同步发电机有功控制器,子模块电容电压控制回路如图 4所示。其中,PI为比例积分控制器;Usmref为子模块电容电压参考值。

|
图 4 子模块电容电压控制框图 Fig. 4 Block diagram of sub-module capacitor voltage control |
该模块计算输出功率的参考指令,此参考值再输入上述虚拟同步发电机控制算法中参与有功控制。这样既保证了稳态运行时子模块电容电压稳定,即M3C输入输出功率守恒,又可以把M3C的功率平衡引入到虚拟同步发电机控制算法当中,在系统频率发生变化的情况下,子模块电容中储存的能量投入参与频率调节,此时子模块电容电压必然会发生变化,子模块电容电压控制回路的作用是逐渐减小实际子模块电容电压与参考值之间的偏差,尽快使其恢复稳定。
有功控制器的总体控制框图如图 5所示。

|
图 5 虚拟同步发电机控制有功控制框图 Fig. 5 Active power control block diagram of virtual synchronous generator control |
M3C无功控制器的控制目标与同步发电机励磁调节器的作用一致,因此M3C无功控制器主要模拟励磁调节器的外特性,最终达到控制M3C输出电压稳定的效果。文中在M3C工频侧无功控制中采用Q-V下垂特性。
| $ Q_{\text {ref }}-Q_{\mathrm{e}}=D_{\mathrm{q}}\left(V_1-V_0\right) $ | (17) |
式中:Qe为实际流过PCC的无功功率;Qref为流过PCC的无功功率的参考值;Dq为Q-V下垂系数;V1为PCC电压有效值;V0为电网额定电压有效值。
在并网运行模式下,无功功率指令值须根据风机出力波动和电网负荷波动适当调整,因此在上述Q-V下垂控制的基础上叠加一个积分控制,以实现对无功功率指令的良好跟踪特性。同时为了维持输出电压稳定在系统额定电压附近,采用虚拟电动势波动值ΔE与系统额定电压幅值E0相加的方式,生成实时的虚拟电动势幅值E,如图 6所示。虚拟同步无功控制器能够响应系统无功负荷的变化作出相应调节,实现无功功率的跟踪调节、维持系统电压的平衡稳定。

|
图 6 虚拟同步发电机控制无功控制框图 Fig. 6 Reactive power control block diagram of virtual synchronous generator control |
图 7为M3C工频侧简化等效电路,为方便分析,图中忽略了变压器。M3C通过PCC向工频系统注入功率,其相电压幅值为V并假设PCC电压相角为0;M3C的虚拟相电动势幅值为E,相角为δ。其中L′s=Lf+L/3,为M3C的虚拟定子电抗;R′s=Rf+R/3,为M3C的虚拟定子电阻。

|
图 7 M3C工频侧简化等效电路 Fig. 7 Simplified equivalent circuit of M3C power frequency side |
该系统的动态功率传输过程与互联的同步发电机系统相同,则M3C工频侧输出功率可以表示为:
| $ S=P_{{\rm{e}}^{\prime}}+\mathrm{j} Q_{{\rm{e}}^{\prime}}=\frac{3 E V \sin \delta}{X}+\mathrm{j} \frac{3 E(E-V \cos \delta)}{X} $ | (18) |
式中:Pe′为M3C工频侧有功功率;Qe′为M3C工频侧无功功率。
结合2.1节和2.2节可知,虚拟同步发电机控制的有功控制器和无功控制器可以直接与系统外电路形成闭环控制。但M3C通常用于中高压系统,系统发生故障时产生的故障电流较大,为了防止换流阀过流,须通过内部电流控制回路来限制故障电流。同时M3C不需要滤波电容,无须采用电压电流双闭环控制,因此文中仅采用内环电流控制。
为了完成电压矢量信号到电流参考值的转化,须设定一个虚拟定子阻抗模块。虚拟定子阻抗控制器主要利用定子绕组电压平衡方程来建立输出电压与输出电流之间的关系,不考虑绕组间的相互作用,如式(19)所示。
| $ \boldsymbol{e}_{\mathrm{s}}-\boldsymbol{v}_{\mathrm{s}}=R_{\mathrm{s}} \boldsymbol{i}_{\mathrm{s}}+L_{\mathrm{s}} \frac{\mathrm{~d} \boldsymbol{i}_{\mathrm{s}}}{\mathrm{~d} t} $ | (19) |
对式(19)进行dq变换可得:
| $ \left\{\begin{array}{l} e_{\mathrm{s} d}-v_{\mathrm{s} d}=R_{\mathrm{s}} i_{\mathrm{s} d}+L_{\mathrm{s}} \frac{\mathrm{~d} i_{\mathrm{s} d}}{\mathrm{~d} t}-\omega_{\mathrm{s}} L_{\mathrm{s}} i_{\mathrm{s} q} \\ e_{\mathrm{s} q}-v_{\mathrm{s} q}=R_{\mathrm{s}} i_{\mathrm{s} q}+L_{\mathrm{s}} \frac{\mathrm{~d} i_{\mathrm{s} q}}{\mathrm{~d} t}+\omega_{\mathrm{s}} L_{\mathrm{s}} i_{\mathrm{s} q} \end{array}\right. $ | (20) |
式中:esd、esq分别为M3C工频侧桥臂输出电压d、q分量;vsd、vsq分别为工频侧PCC处电压d、q分量;isd、isq分别为M3C工频侧输出电流d、q分量。
对式(20)进行拉普拉斯变换并忽略动态矢量过程和耦合项可得:
| $ \left[\begin{array}{c} i_{\mathrm{s} d} \\ i_{{{\rm{s}}q}} \end{array}\right]=\frac{R_{\mathrm{s}}}{R_{\mathrm{s}}^2+X_{\mathrm{s}}^2}\left[\begin{array}{l} e_{\mathrm{s} d}-v_{\mathrm{s} d} \\ e_{{{\rm{s}}q}}-v_{\mathrm{s} q} \end{array}\right] $ | (21) |
由式(21)可知,发电机定子绕组输出电流与感应电动势和端电压的差值成比例。因此可以引入一个比例系数来模拟定子绕组的动态特性,输出内环电流控制器所需的电流指令值isdref、isqref,如式(22)所示,其中Kz_p为比例系数。
| $ \left[\begin{array}{c} i_{\mathrm{s} d \mathrm{ref}} \\ i_{\mathrm{s} q \mathrm{ref}} \end{array}\right]=K_{\mathrm{z} \_\mathrm{p}}\left[\begin{array}{l} e_{\mathrm{s} d}-v_{\mathrm{s} d} \\ e_{\mathrm{s} q}-v_{\mathrm{s} q} \end{array}\right] $ | (22) |
电流控制器设计采用典型双dq解耦内环电流控制。其控制方程如式(23)所示,ixd、ixq分别为x相子换流器电流d、q分量,x=u, v, w;vxd、vxq分别为x相子换流器电压d、q分量;kc_p、kc_i分别为PI控制器比例、积分参数;ixdref、ixqref分别为x相子换流器电流d、q分量参考值。
| $ \left\{\begin{aligned} v_{x d}=-v_{\mathrm{s} d}+ & \omega_{\mathrm{c}} L i_{x q}-k_{\mathrm{c}_{-} \mathrm{p}}\left(i_{x d}^{\mathrm{ref}}-i_{x d}\right)- \\ & k_{\mathrm{c}-\mathrm{i}}\left(i_{x d}^{\mathrm{ref}}-i_{x d}\right) \mathrm{d} t \\ v_{x q}=-v_{{{\rm{s}}q}}- & \omega_{\mathrm{c}} L i_{x d}-k_{c_{-\mathrm{p}}}\left(i_{x q}^{\mathrm{ref}}-i_{x q}\right)- \\ & k_{\mathrm{c}-\mathrm{i}} \int\left(i_{x q}^{\mathrm{ref}}-i_{x d}\right) \mathrm{d} t \end{aligned}\right. $ | (23) |
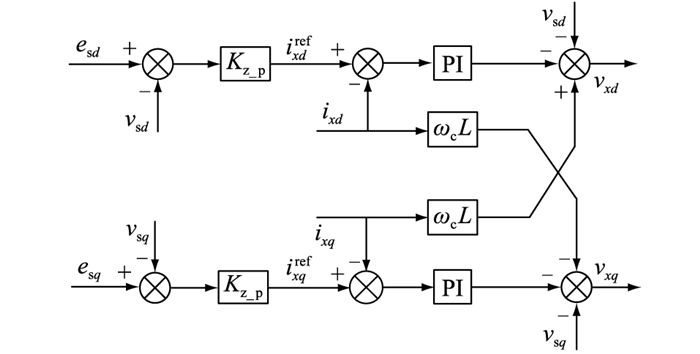
此时内环电流控制器解耦所需的角频率和进行dq变换所需的相角是由有功控制器所提供的,不依赖于锁相环。综合式(22)和式(23)可以得出虚拟定子阻抗控制器和电流控制器的控制框图,如图 8所示。
|
图 8 虚拟定子阻抗控制器和电流控制器的控制框图 Fig. 8 Control block diagram of virtual stator impedance controller and current controller |
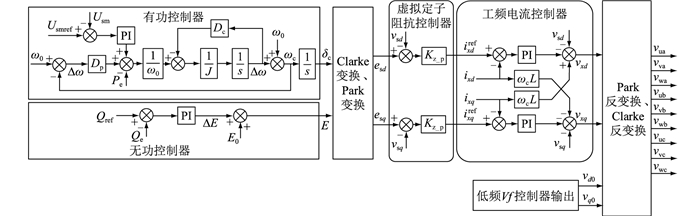
如图 9所示,子模块电容电压控制模块、下垂控制模块和转子运动方程控制模块构成了有功控制器,正常运行时能够维持子模块电容电压平衡,系统频率变化时变频器可以参与调频,并且使变频器具有惯性和阻尼特性,输出虚拟电动势相角和变频器虚拟角速度,为内部电流解耦控制提供了参数。无功控制器能够跟踪无功功率指令,维持系统电压稳定运行,输出虚拟电动势幅值。有功控制器和无功控制器输出的电压矢量经派克变换变为直流量,通过虚拟定子阻抗控制器生成内环电流参考值,经过内环电流解耦控制,得到工频侧dq轴桥臂电压信号。该信号经过坐标变换后与低频侧桥臂电压信号叠加,从而得到abc坐标系下的桥臂电压信号。
|
图 9 虚拟同步发电机控制整体控制框图 Fig. 9 The overall control block diagram of virtual synchronous generator control |
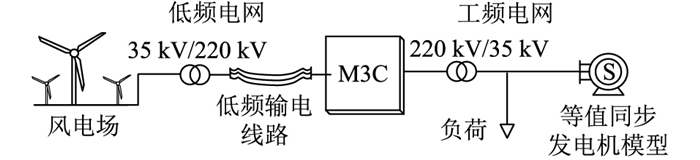
在PSCAD/EMTDC仿真平台搭建基于虚拟同步发电机控制的M3C仿真模型,系统拓扑如图 10所示。风机经过变压器连接220 kV低频电网,经海底电缆与M3C低频侧相连,M3C工频侧与220 kV工频电网相连,工频电网由等值同步发电机模型和负荷组成。系统主要参数如表 1所示。
|
图 10 海上风电低频输电系统拓扑 Fig. 10 Topology of offshore wind power low frequency transmission system |
|
|
表 1 系统主要参数 Table 1 Main parameters of the system |
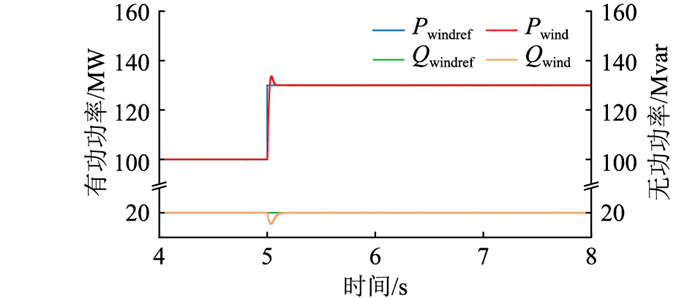
在0 s—5 s期间,风电机组有功输出100 MW,无功输出20 Mvar,5 s时风电机组有功功率指令值由100 MW变化为130 MW,仿真结果如图 11—图 15所示。
|
图 11 风电机组输出功率 Fig. 11 Output power of wind turbine |
|
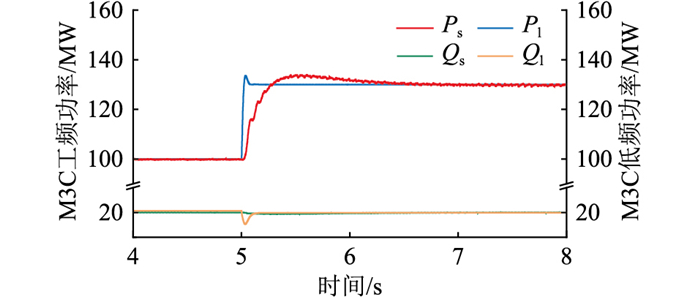
图 12 M3C工频侧和低频侧功率 Fig. 12 The power of M3C power frequency side and low frequency side |

|
图 13 工频侧三相电流 Fig. 13 Three-phase current of power frequency side |

|
图 14 工频侧三相电压 Fig. 14 Three-phase voltage of power frequency side |
|
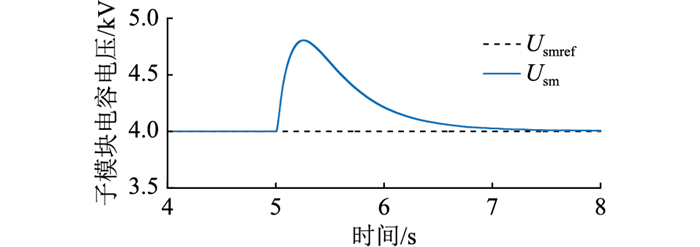
图 15 虚拟同步发电机控制下子模块电容电压 Fig. 15 Sub-module capacitance voltage with virtual synchronous generator control |
图 11为风电机组输出功率。从图中可知,虚拟同步发电机控制下风机输出的有功功率Pwind与无功功率Qwind均能够稳定跟踪其指令值Pwindref、Qwindref。图 12为M3C工频侧有功和无功功率Ps、Qs以及低频侧有功和无功功率Pl、Ql的变化情况,在风机有功功率变化后,M3C两侧的功率可以过渡到新的稳定状态,并且工频侧有功功率达到稳态的时间更长,功率变化率更小,说明换流器具有惯量特性,同时内部有能量参与系统调节。
图 13、图 14分别为工频侧三相电流和电压,当风机有功功率增加时,M3C工频侧能够保持电压幅值不变,电流幅值随功率的增加而增加,并且稳定三相对称运行。
图 15为M3C子模块电容电压,当风电机组输出有功功率增大时,M3C子模块电容暂时吸收能量,抑制工频系统频率的上升,稳定后电容电压又恢复电压指令值稳定运行。
由以上仿真结果可知,在虚拟同步发电机控制策略下,分频海上风电系统能够保持稳定运行,当风电系统的工况改变时,M3C能够通过控制器跟踪控制指令,具有良好的动态性能。
3.2 不同控制策略下分频海上风电系统仿真对比文献[21]提出了经典双dq坐标变换解耦控制策略,控制结构简单,各电气量物理概念清晰,并且控制方案中所有的被控量都是直流量,相比以往文献在αβ坐标系下的控制方案更易实现控制的无静差特性和优良的动态性能,是目前M3C研究领域主流控制策略,因此文中基于该控制策略对虚拟同步发电机控制策略进行仿真对比研究。
采用图 10所示拓扑和表 1所示系统参数搭建仿真模型。通常从频率调节的角度来看,在海上风电送出的典型场景下,电力系统最常见的干扰是风速变化导致风机出力发生变化,下文分情况分析比较2种控制系统的动态响应。
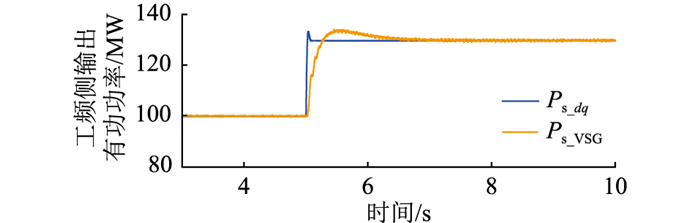
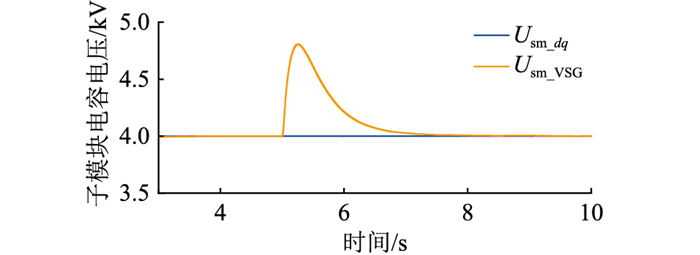
(1) 工况1:风电机组出力阶跃式突增。t=5 s时,风电机组输出有功功率指令值从100 MW阶跃突变为130 MW,无功功率保持20 Mvar不变,其仿真结果对比如图 16—图 18所示。其中,fs_dq、fs_VSG分别为传统控制方式和文中控制方式下工频侧输电频率;Ps_dq、Ps_VSG分别为传统控制方式和文中控制方式下M3C工频侧有功功率;Usm_dq、Usm_VSG分别为传统控制方式和文中控制方式下M3C子模块电容电压。

|
图 16 工频侧输电频率(工况1) Fig. 16 Transmission frequency at power frequency side (case 1) |
|
图 17 M3C工频侧有功功率(工况1) Fig. 17 Active power of M3C power frequency side (case 1) |
|
图 18 子模块电容电压(工况1) Fig. 18 Sub-module capacitance voltage (case 1) |
由图 16可知,虚拟同步发电机控制下,工频电网频率的最大波动差值相较解耦控制降低了10%,在系统稳定后电网频率的稳态值与解耦控制几乎相同,说明2种控制策略均能实现电网频率的稳定控制,但虚拟同步发电机控制存在惯量特性,故频率调节更平滑,系统的频率波动更低。
图 17为M3C工频侧有功功率,相较解耦控制,虚拟同步发电机控制有功功率增速更缓慢,从而减小风速突变对系统频率的冲击。
图 18为M3C子模块电容电压,可以看出传统dq解耦控制子模块电容电压几乎稳定在额定电压,不参与系统的频率调节;虚拟同步发电机控制下M3C通过子模块电容吸收多余的有功功率,子模块电容电压升高,从而调节系统频率,降低频率波动。
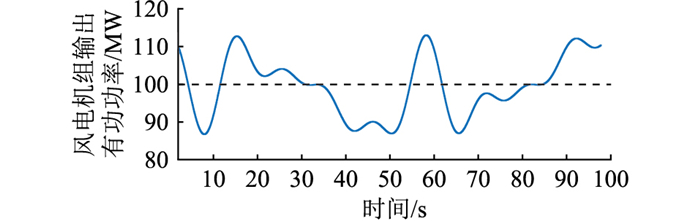
(2) 工况2:风电机组出力持续波动。假设风电机组有功出力在100 MW持续随机波动,有功功率波动如图 19所示。2种控制策略仿真结果对比如图 20、图 21所示。
|
图 19 风电机组输出有功功率 Fig. 19 Wind turbine output active power |
|
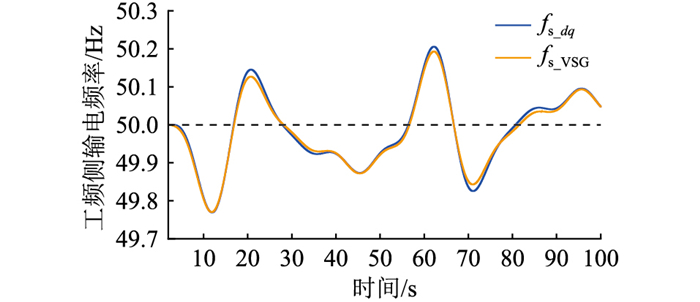
图 20 工频侧输电频率(工况2) Fig. 20 Transmission frequency at power frequency side (case 2) |
|
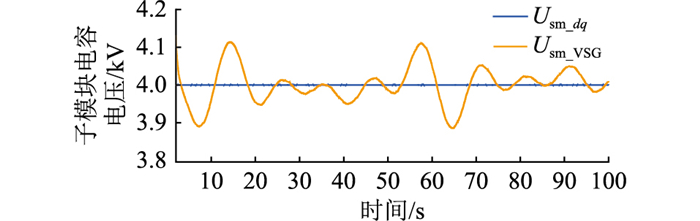
图 21 子模块电容电压(工况2) Fig. 21 Sub-module capacitance voltage (case 2) |
图 20为工频侧输电频率,在2种控制策略下,工频频率均随风电机组出力变化在50 Hz附近波动,对2种控制策略下工频频率波动进行量化分析,如表 2所示。可见,虚拟同步发电机控制下工频频率绝对平均误差和方差均低于传统dq解耦控制,说明虚拟同步发电机控制工频频率波动更小,系统惯量特性增强。
|
|
表 2 2种控制策略工频频率波动量化比较 Table 2 Quantitative comparison of power frequency frequency fluctuation of two control strategies |
图 21为M3C子模块电容电压,可以看出虚拟同步发电机控制下M3C通过子模块的充放电参与频率调节,子模块电容电压根据风电机组出力的变化在额定电压附近波动。由于未考虑桥臂电容容量的设计,M3C子模块电容中可用于调节的能量较小,风机出力持续波动情况下虚拟同步发电机控制对于频率的调节作用有一定局限。
4 结语文中针对M3C变频器控制策略展开研究,将M3C数学模型变形化简后与同步发电机的数学模型进行对比,得出M3C与同步发电机在系统结构、参数和运动方程上具有极高的对应性和一致性。结合转子运动方程、调速器和励磁调节器的功能,设计了虚拟有功控制器和无功控制器,使变频器具有惯性和阻尼特性并且能够参与系统频率调节和维持电压稳定。同时加入子模块电容电压控制,保证正常运行时子模块电容电压在指令值附近保持稳定。为了避免系统故障导致换流阀过流,设计了虚拟定子阻抗控制器和电流控制器。结合分频海上风电系统拓扑,形成了低频侧采用Vf控制,工频侧采用虚拟同步发电机控制的整体控制策略。最后通过仿真验证了虚拟同步发电机控制策略的可行性,并通过比较不同控制策略下的仿真结果说明了文中设计的控制策略的优越性。
实际工程中,考虑到桥臂电容容量的设计和子模块电压波动的限制,M3C子模块电容中可用于电压频率调节的能量较小,因此虚拟转动惯量选择不大,对系统惯量支撑能力较弱,后续将研究加装储能系统或者与风电机组配合条件下M3C虚拟同步发电机控制策略,进一步提升M3C的惯量支撑能力。
致谢
本文得到国网江苏省电力有限公司科技项目“中远海风电柔性低频输电送出关键技术及装备”(J2022032)资助,谨此致谢!
| [1] |
王秀丽, 赵勃扬, 黄明煌, 等. 大规模深远海风电送出方式比较及集成设计关键技术研究[J]. 全球能源互联网, 2019, 2(2): 138-145. WANG Xiuli, ZHAO Boyang, HUANG Minghuang, et al. Research of integration methods comparison and key design technologies for large scale long distance offshore wind power[J]. Journal of Global Energy Interconnection, 2019, 2(2): 138-145. (  0) 0) |
| [2] |
孙玉巍, 常静恬, 付超, 等. 分频输电系统模块化多电平矩阵变换器谐波特性分析[J]. 电力工程技术, 2022, 41(5): 21-30, 84. SUN Yuwei, CHANG Jingtian, FU Chao, et al. Harmonic characteristics analysis of modular multilevel matrix converter for fractional frequency transmission system[J]. Electric Power Engineering Technology, 2022, 41(5): 21-30, 84. (  0) 0) |
| [3] |
段子越, 孟永庆, 孔颖, 等. 分频输电系统高频隔离型换流器拓扑与经济性研究[J]. 浙江电力, 2022, 41(1): 71-79. DUAN Ziyue, MENG Yongqing, KONG Ying, et al. Research on topology and economy of high-frequency isolated AC/AC converter in fractional frequency transmission system[J]. Zhejiang Electric Power, 2022, 41(1): 71-79. (  0) 0) |
| [4] |
迟永宁, 梁伟, 张占奎, 等. 大规模海上风电输电与并网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(14): 3758-3770. CHI Yongning, LIANG Wei, ZHANG Zhankui, et al. An overview on key technologies regarding power transmission and grid integration of large scale offshore wind power[J]. Proceedings of the CSEE, 2016, 36(14): 3758-3770. (  0) 0) |
| [5] |
张翀, 李宽宏, 张轩, 等. 六角形模块化多电平AC/AC换流器损耗特性分析计算[J]. 电力系统自动化, 2019, 43(13): 105-113. ZHANG Chong, LI Kuanhong, ZHANG Xuan, et al. Analysis and calculation of loss characteristics for hexagonal modular multilevel AC/AC converter[J]. Automation of Electric Power Systems, 2019, 43(13): 105-113. DOI:10.7500/AEPS20180620005 (  0) 0) |
| [6] |
GLINKA M, MARQUARDT R. A new AC/AC multilevel converter family[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 662-669. DOI:10.1109/TIE.2005.843973 (  0) 0) |
| [7] |
唐英杰, 张哲任, 徐政. 基于有源型M3C矩阵变换器的海上风电低频送出方案[J]. 电力系统自动化, 2022, 46(8): 113-122. TANG Yingjie, ZHANG Zheren, XU Zheng. Low-frequency transmission scheme for offshore wind power based on active modular multilevel matrix converter[J]. Automation of Electric Power Systems, 2022, 46(8): 113-122. (  0) 0) |
| [8] |
王文杰, 杨益平, 杭丽君, 等. 应用于交-交变换的M3C矩阵变换器系统控制策略[J]. 电力系统自动化, 2020, 44(12): 186-192. WANG Wenjie, YANG Yiping, HANG Lijun, et al. Control strategy of M3C matrix converter system applied to AC-AC transformation[J]. Automation of Electric Power Systems, 2020, 44(12): 186-192. (  0) 0) |
| [9] |
ANGKITITRAKUL S, ERICKSON R W. Control and implementation of a new modular matrix converter[C]//Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition. Anaheim, CA, USA. IEEE, 2004: 813-819.
(  0) 0) |
| [10] |
ANGKITITRAKUL S, ERICKSON R W. Capacitor voltage balancing control for a modular matrix converter[C]//Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition. Dallas, TX, USA. IEEE, 2006: 7.
(  0) 0) |
| [11] |
KAWAMURA W, HAGIWARA M, AKAGI H. Control and experiment of a 380-V, 15-kW motor drive using modular multilevel cascade converter basedon triple-star bridge cells(MMCC-TSBC)[C]//2014 International Power Electronics Conference. Hiroshima, Japan. IEEE, 2014: 3742-3749.
(  0) 0) |
| [12] |
KAWAMURA W, CHENK L, HAGIWARA M, et al. A low-speed, high-torque motor drive using the modular multilevel cascade converter based on triple-star bridge cells (MMCC-TSBC)[C]//2014 IEEE Energy Conversion Congress and Exposition(ECCE). Pittsburgh, PA, USA. IEEE, 2014: 1631-1638.
(  0) 0) |
| [13] |
李峰, 王广柱. 模块化多电平矩阵变换器输入输出频率相近时低频运行控制策略[J]. 电工技术学报, 2016, 31(22): 107-114. LI Feng, WANG Guangzhu. Control strategy for low frequency operation of modular multilevel matrix converters with similar input and output frequencies[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 107-114. DOI:10.3969/j.issn.1000-6753.2016.22.014 (  0) 0) |
| [14] |
WU Q, WANG G Z, FENG J Z, et al. A novel comprehensive control scheme of modular multilevel converter-based power electronic transformer[C]//2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies(DRPT). Changsha, China. IEEE, 2015: 2253-2258.
(  0) 0) |
| [15] |
李峰, 王广柱, 刘汝峰. 扩展模块化多电平矩阵变换器低频运行范围的控制方法[J]. 电力系统自动化, 2016, 40(22): 132-138, 153. LI Feng, WANG Guangzhu, LIU Rufeng. Control scheme of modular multilevel matrix converters for expanding low-frequency operating range[J]. Automation of Electric Power Systems, 2016, 40(22): 132-138, 153. (  0) 0) |
| [16] |
OU Z J, WANG G Z. Multi-hierarchy control strategy in abc coordinate for modular multilevel matrix converter in fractional frequency transmission system[J]. The Journal of Engineering, 2019(16): 1886-1891. (  0) 0) |
| [17] |
KAWAMURA W, HAGIWARA M, AKAGI H. A broad range of frequency control for the modular multilevel cascade converter based on triple-star bridge-cells (MMCC-TSBC)[C]//2013 IEEE Energy Conversion Congress and Exposition. Denver, CO, USA. IEEE, 2013: 4014-4021.
(  0) 0) |
| [18] |
KAMMERER F, KOLB J, BRAUN M. Fully decoupled current control and energy balancing of the modular multilevel matrix converter[C]//2012 15th International Power Electronics and Motion Control Conference. Novi Sad, Serbia. IEEE, 2012: 3-8.
(  0) 0) |
| [19] |
KAWAMURA W, HAGIWARA M, AKAGI H. Control and experiment of a modular multilevel cascade converter based on triple-star bridge cells[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3536-3548. DOI:10.1109/TIA.2014.2311759 (  0) 0) |
| [20] |
KAWAMURA W, AKAGI H. Control of the modular multilevel cascade converter based on triple-star bridge-cells (MMCC-TSBC) for motor drives[C]//2012 IEEE Energy Conversion Congress and Exposition. Raleigh, NC, USA. IEEE, 2012: 3506-3513.
(  0) 0) |
| [21] |
孟永庆, 王健, 李磊, 等. 基于双dq坐标变换的M3C变换器的数学模型及控制策略研究[J]. 中国电机工程学报, 2016, 36(17): 4702-4711. MENG Yongqing, WANG Jian, LI Lei, et al. Research on modeling and control strategy of modular multilevel matrix converter based on double dq coordinate transformation[J]. Proceedings of the CSEE, 2016, 36(17): 4702-4711. (  0) 0) |
| [22] |
孙玉巍, 王童, 付超, 等. 适用于海上风电分频输电的模块化多电平矩阵变换器故障穿越控制策略[J]. 高电压技术, 2023, 49(1): 19-30. SUN Yuwei, WANG Tong, FU Chao, et al. Fault ride-through control strategy of modular multilevel matrix converter for fractional frequency transmission system[J]. High Voltage Engineering, 2023, 49(1): 19-30. (  0) 0) |
| [23] |
郑涛, 宋伟男, 吕文轩. 基于M3C的低频输电系统不对称故障穿越控制策略[J]. 电力系统保护与控制, 2023, 51(8): 107-117. ZHENG Tao, SONG Weinan, LÜ Wenxuan. Asymmetric fault ride-through control strategy for a low frequency AC transmission system based on a modular multilevel matrix converter[J]. Power System Protection and Control, 2023, 51(8): 107-117. (  0) 0) |
| [24] |
BECK H P, HESSE R. Virtual synchronous machine[C]//2007 9th International Conference on Electrical Power Quality and Utilisation. Barcelona, Spain. IEEE, 2007: 1-6.
(  0) 0) |
| [25] |
ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267. DOI:10.1109/TIE.2010.2048839 (  0) 0) |
| [26] |
ZHONG Q C, NGUYEN P L, MA Z Y, et al. Self-synchronized synchronverters: inverters without a dedicated synchronization unit[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 617-630. DOI:10.1109/TPEL.2013.2258684 (  0) 0) |
| [27] |
龚仁喜, 顾佳宇. 负荷虚拟同步机惯性与阻尼自适应控制策略[J]. 电测与仪表, 2023, 60(3): 130-135. GONG Renxi, GU Jiayu. Adaptive control strategy of inertia and damping for load virtual synchronous machine[J]. Electrical Measurement & Instrumentation, 2023, 60(3): 130-135. (  0) 0) |
| [28] |
方仍存, 雷何, 杨东俊, 等. 变流器辅助换流的柔性切换开关拓扑与控制[J]. 电力工程技术, 2023, 42(1): 43-49, 123. FANG Rengcun, LEI He, YANG Dongjun, et al. A converter-assisting flexible switch topology and its control strategy[J]. Electric Power Engineering Technology, 2023, 42(1): 43-49, 123. (  0) 0) |
| [29] |
许崇福, 李菀茹, 徐宁一, 等. 应用于储能变流器的虚拟同步发电机阻尼特性分析与改进[J]. 电网技术, 2020, 44(5): 1656-1663. XU Chongfu, LI Wanru, XU Ningyi, et al. Analysis and improvement of damping characteristics of virtual synchronous generator control applied to energy storage converter[J]. Power System Technology, 2020, 44(5): 1656-1663. (  0) 0) |
| [30] |
禹海峰, 马俊杰, 周年光, 等. 面向储能惯量支撑能力评估的新型电力系统惯性系数辨识方法[J]. 智慧电力, 2023, 51(5): 1-7, 72. YU Haifeng, MA Junjie, ZHOU Nianguang, et al. New power system inertia coefficient identification method for energy storage inertia support capability evaluation[J]. Smart Power, 2023, 51(5): 1-7, 72. (  0) 0) |
| [31] |
田艳军, 彭飞, 朱晓荣, 等. 直流微网储能单元的灵活类虚拟同步发电机控制[J]. 高电压技术, 2020, 46(7): 2316-2326. TIAN Yanjun, PENG Fei, ZHU Xiaorong, et al. Flexible analogous virtual synchronous generator control for energy storage units in DC microgrid[J]. High Voltage Engineering, 2020, 46(7): 2316-2326. (  0) 0) |
| [32] |
董存, 陶以彬, 张牟发, 等. 基于虚拟同步发电机的逆变器类电源频率特性及重塑技术[J]. 电力建设, 2022, 43(2): 109-116. DONG Cun, TAO Yibin, ZHANG Moufa, et al. Frequency characteristics and reshaping technology for inveter-based generators based on virtual synchronous generator[J]. Electric Power Construction, 2022, 43(2): 109-116. (  0) 0) |
| [33] |
于晶荣, 孙文, 于佳琪, 等. 基于惯性自适应的并网逆变器虚拟同步发电机控制[J]. 电力系统保护与控制, 2022, 50(4): 137-144. YU Jingrong, SUN Wen, YU Jiaqi, et al. Virtual synchronous generator control of a grid-connected inverter based on adaptive inertia[J]. Power System Protection and Control, 2022, 50(4): 137-144. (  0) 0) |
| [34] |
郑天文, 陈来军, 陈天一, 等. 虚拟同步发电机技术及展望[J]. 电力系统自动化, 2015, 39(21): 165-175. ZHENG Tianwen, CHEN Laijun, CHEN Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175. (  0) 0) |
2. Xi'an Jiaotong University (State Key Laboratory of Electrical Insulation and Power Equipment), Xi'an 710049, China

 ,
,  韩华春(1988), 女, 博士, 高级工程师, 从事新能源并网控制技术相关工作(E-mail:
韩华春(1988), 女, 博士, 高级工程师, 从事新能源并网控制技术相关工作(E-mail: