文章编号: 2096-3203(2022)06-0013-08 中图分类号: TM732
2. 国网上海市电力公司浦东供电公司, 上海 200120;
3. 国网上海市电力公司, 上海 200122
随着量测与通信技术的发展,城市中智能楼宇的数目不断增加,电动汽车和空调的数目与容量也大幅增加。电动汽车和空调在作为负荷的同时,因具备良好的功率实时响应潜力而成为智能楼宇中重要的需求侧资源[1-4]。智能楼宇具有巨大的峰值负荷削减潜力,加强其运行调控将具有相当可观的经济效益和社会效益,但其产消行为具有强不确定性,因此须解决智能楼宇中需求侧资源运行无序、分散且单体可调容量小的难点[5]。
目前需求侧资源主要采用用户自主控制,如电动汽车的充放电具有随机无序性、空调负荷在不同用户的温度设置下独立运行等,但这种控制存在感知能力差、响应速度慢等问题,不能满足电力系统的实时功率平衡调度需求。多种需求侧资源间缺乏协同调控,无法参与到电力系统中,发挥其资源价值[6]。因此,利用虚拟电厂(virtual power plant, VPP)[7]这一方式规模化地聚合智能楼宇中的需求侧资源以参与到电力系统调控中是重要的研究方向。
电动汽车与空调负荷具有良好的功率实时响应潜力,使得由电动汽车和空调负荷构成的VPP参与到调频辅助服务中成为可能。目前已有文献对电动汽车和空调负荷参与调频辅助服务进行研究。文献[8-9]分别通过实验验证了电动汽车和变频热泵在提供调频服务上的可行性;文献[10]提出了电动汽车参与调频辅助服务的模型预测控制方法,改善了跟踪误差和电池循环;文献[11]提出了一种用于互联电源和空调负荷的需求响应负荷跟踪策略,跟踪系统中的不匹配功率,优化系统频率性能。以上文献均只对单一类型的需求侧资源进行调控,并未考虑2种资源的联合调控。
VPP参与电力系统调频辅助服务需要在日前耦合用电功率和调频容量并上报,同时需要考虑用户需求,然而调频信号涉及整个电网的供需不平衡,难以预测且不确定性较大[12]。已有研究对调频信号在日前申报阶段的不确定性进行分析。文献[13]建立了基于性能补偿方案下的电动汽车调频辅助服务模型,采用鲁棒优化框架描述调频容量调度问题。但鲁棒优化受限于不确定集的准确性,在难以确定不确定集的情况下会导致模型过于保守[14]。文献[15]利用模糊集理论对电力市场预测数据中的不确定性进行建模,提出了在辅助服务最优时报价的策略,但模糊规划需要依据决策者的个人经验来获取不确定参数的模糊隶属函数,在实际应用中存在诸多限制。此外,在实时功率的分配上,现有文献往往从满足用户需求的角度进行分析, 未考虑实时功率分配阶段的用户侧成本[16-17]。
针对以上问题,文中首先建立集中式控制框架下包含电动汽车与空调负荷的智能楼宇型VPP聚合模型,建立虚拟储能模型以评判VPP调度潜力。其次,对调频信号的不确定性进行分析,建立基于机会约束的VPP日前优化调度模型,耦合日前能量功率和调频容量。然后,在实时功率分配阶段,提出考虑用户侧成本的功率分配策略,降低VPP整体运行成本,实现多目标的协调运行。最后,通过仿真算例验证所提策略的可行性与有效性。
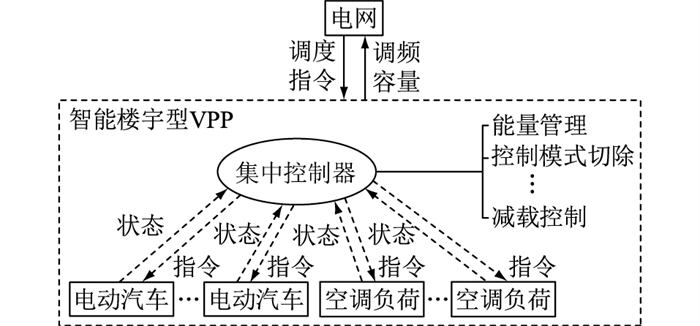
1 智能楼宇型VPP参与调频辅助服务的运行机制 1.1 智能楼宇型VPP运行框架智能楼宇型VPP由电动汽车和空调负荷聚合而成,通过与控制中心进行信息通信,实现与大电网的能量交互。智能楼宇型VPP采用集中式控制架构,如图 1所示。在VPP中设立集中控制器,收集分布式运行的所有单元的状态信息,包括电动汽车接入情况与电量、空调使用情况和室内温度等,并对这些信息进行实时处理,计算和预测VPP可用调频容量并上报电网。同时,在接收电网的调频信号后,集中控制器将下达控制指令,将调频功率分配到各成员,协调内部资源。电动汽车和空调负荷采用就地控制器,将状态信息上传至集中控制器,并接收调频信号。
|
图 1 智能楼宇型VPP运行框架 Fig. 1 Operation framework of smart building-based VPP |
在市场机制方面,参考美国PJM电力市场的辅助服务交易机制。VPP参与辅助服务分为日前和日内2个阶段。在日前,VPP通过预测自身出力,上报每个时段的能量出力和调频备用,每个时段的时间长度为1 h;在日内,调度中心根据VPP的竞标结果下发每个时刻VPP的出力信号,时间粒度为2 s,并考核调频里程和调频性能。
将VPP参与调频辅助服务市场的总时长分为m个时段。在i时段t时刻,VPP需要响应的功率Pttotal为:
| $ P_t^{{\rm{total }}} = P_t^{\rm{E}} + P_t^{{\rm{FR}}} $ | (1) |
式中:PtE为需要在能量市场响应的功率;PtFR为需要在调频市场响应的功率。PtFR由VPP在调频市场竞标的调频容量乘以调频信号得到,即:
| $ P_t^{{\rm{FR}}} = {R_i}{\delta _t} $ | (2) |
式中:Ri为VPP在i时段的调频容量;δt为调度中心下发的调频信号,取值范围为[-1, 1]。
在VPP响应后,调度中心会计算调频里程和调频性能。
| $ {M_i} = \sum\limits_{t = 2}^n {\left| {\left( {P_t^{{\rm{FR}}} - P_{t - 1}^{{\rm{FR}}}} \right)} \right|} $ | (3) |
| $ {A_i} = 1 - \sum\limits_{t = 1}^n {\left| {P_t^{{\rm{FR}}} - P_t^{{\rm{RR}}}} \right|} /\sum\limits_{t = 1}^n {\left| {P_t^{{\rm{FR}}}} \right|} $ | (4) |
式中:Mi为i时段的里程;Ai为调频性能指标,文中只考虑精确度分数,不考虑相关性分数和延迟分数;PtRR为VPP实际响应的调频功率;n为i时段调频信号的数量。
调度中心根据计算得到的里程和调频性能指标来计算VPP在调频市场的收益,分为容量收益和里程收益。
| $ \left\{ {\begin{array}{*{20}{l}} {C_i^{{\rm{FR}}} = C_i^{{\rm{cap}}} + C_i^{{\rm{mil}}}}\\ {C_i^{{\rm{cap}}} = {R_i}\pi _i^{{\rm{cp}}}{A_i}}\\ {C_i^{{\rm{mil}}} = {M_i}\pi _i^{{\rm{mp}}}{A_i}} \end{array}} \right. $ | (5) |
式中:CiFR为调频市场的总收益;Cicap,Cimil分别为调频容量收益和调频里程收益;πicp,πimp分别为容量价格和里程价格。
在收益结算中,调频性能指标非常重要,因此需要合理配置能量市场的功率和调频容量,以提高调频性能指标。
VPP的总收益CiVPP为能量市场收益CiE和调频市场收益CiFR之和。
| $ C_i^{{\rm{VPP}}} = C_i^{\rm{E}} + C_i^{{\rm{FR}}} $ | (6) |
以智能楼宇中的电动汽车为研究目标,设定电动汽车的到达时间、离开时间和初始荷电状态(state of charge, SOC)均服从正态分布[18]。
电动汽车电池SOC与电池充放电功率的关系为:
| $ \begin{array}{c} S_{k, t}^{{\rm{EV}}} = S_{k, t - 1}^{{\rm{EV}}} + \left\{ {\left[ {{\eta _{\rm{c}}}/2 + 1/\left( {2{\eta _{\rm{d}}}} \right)} \right]P_{k, t}^{{\rm{EV}}} + } \right.\\ \left. {\left[ {{\eta _{\rm{c}}}/2 - 1/\left( {2{\eta _{\rm{d}}}} \right)} \right]\left| {P_{k, t}^{{\rm{EV}}}} \right|} \right\}\frac{1}{E}\Delta t \end{array} $ | (7) |
式中:Sk, tEV为第k辆电动汽车t时刻的SOC;ηc,ηd分别为电动汽车的充、放电效率;Pk, tEV为第k辆电动汽车t时刻的功率,正值表示充电,负值表示放电;E为电动汽车电池的总容量。
电动汽车群的虚拟储能模型为[19]:
| $ \left\{ {\begin{array}{*{20}{l}} {E_t^{{\rm{EVVB}}} = \sum\limits_{{N_{{\rm{EV}}}}}^{k = 1} E_{k, t}^{{\rm{EV}}}}\\ {P_t^{{\rm{EVVB}}} = \sum\limits_{{N_{{\rm{EV}}}}}^{k = 1} P_{k, t}^{{\rm{EV}}}}\\ {E_t^{{\rm{EVVB}}} = E_{t - 1}^{{\rm{EVVB}}} + \left\{ {\left[ {{\eta _{\rm{c}}}/2 + 1/\left( {2{\eta _{\rm{d}}}} \right)} \right]P_t^{{\rm{EVVB}}} + } \right.}\\ \ \ \ \ \ \ {\left. {\left[ {{\eta _{\rm{c}}}/2 - 1/\left( {2{\eta _{\rm{d}}}} \right)} \right]\left| {P_t^{{\rm{EVVB}}}} \right|} \right\}{\rm{\Delta }}t}\\ {E_t^{{\rm{EVVBmin}}} \le E_t^{{\rm{EVVB}}} \le E_t^{{\rm{EVVBmax}}}} \end{array}} \right. $ | (8) |
式中:Ek, tEV为第k台电动汽车t时刻的能量;EtEVVB,PtEVVB分别为t时刻电动汽车群的能量和功率;NEV为电动汽车的数量;EtEVVBmax,EtEVVBmin分别为电动汽车群最大能量和最小能量。
2.2 空调负荷虚拟储能模型空调负荷可分为定频空调和变频空调2类。定频空调通过控制开关控制温度,功率为恒定值;变频空调则通过控制压缩机的频率来控制功率,可在一定范围内改变功率。文中主要对变频空调的控制策略进行研究,并在夏季降温场景下进行分析。
(1) 热力学模型。采用基于电路模拟的等效热参数(equivalent thermal parameters, ETP)建模方法对建筑进行建模。为简化计算,采用一阶ETP模型进行分析,如图 2所示[2]。其中,Tout为室外温度;Tin为室内温度;QAC为空调制冷量;Ca为等效比热容;R1为等效阻抗。

|
图 2 空调-建筑系统一阶ETP模型 Fig. 2 First-order ETP model of air-conditioning and building system |
其微分方程为:
| $ \frac{{{\rm{d}}{T^{{\rm{in}}}}}}{{{\rm{d}}t}} = \frac{1}{{{R_1}{C_{\rm{a}}}}}\left( {{T^{{\rm{out }}}} - {T^{{\rm{in}}}}} \right) - \frac{{{Q^{{\rm{AC}}}}}}{{{C_{\rm{a}}}}} $ | (9) |
(2) 电热转换模型。空调的电热转换模型用于描述空调制冷量与消耗的电功率之间的关系。变频空调的电功率PAC以及制冷量QAC都与压缩机频率fAC有关,其关系式可表示为[20]:
| $ \left\{ {\begin{array}{*{20}{l}} {{P^{A{\rm{C}}}} = {k_1}{f^{A{\rm{C}}}} + {l_1}}\\ {{Q^{{\rm{AC}}}} = {k_2}{f^{A{\rm{C}}}} + {l_2}} \end{array}} \right. $ | (10) |
式中:k1,k2,l1,l2均为线性模型的系数。
根据式(10)可以求得空调制冷量QAC与电功率PAC之间的关系为:
| $ {Q^{{\rm{AC}}}} = \frac{{{k_2}}}{{{k_1}}}{P^{{\rm{AC}}}} + \frac{{{k_1}{l_2} - {l_1}{k_2}}}{{{k_1}}} $ | (11) |
将单台空调负荷的虚拟储能所储存的能量定义为空调以最大功率运行时,室内温度从温度舒适区上限下降到当前温度时所消耗的能量。即当室内温度处于温度舒适区上限时,空调虚拟储能的能量为0;当室内温度处于温度舒适区下限时,空调虚拟储能的能量达到容量上限。根据式(9)和式(11)可以得出:
| $ E_t^{{\rm{AC}}} = {P^{{\rm{ACmax}}}}{R_1}{C_{\rm{a}}}\ln \frac{{T_t^{{\rm{out }}} - {T^{\max }} - {Q^{{\rm{ACmax}}}}{R_1}}}{{T_t^{{\rm{out }}} - T_t^{{\rm{in }}} - {Q^{{\rm{ACmax}}}}{R_1}}} $ | (12) |
| $ {Q^{{\rm{ACmax}}}} = \frac{{{k_2}}}{{{k_1}}}{P^{{\rm{ACmax}}}} + \frac{{{k_1}{l_2} - {l_1}{k_2}}}{{{k_1}}} $ | (13) |
式中:EtAC为t时刻空调负荷虚拟储能储存的能量,为室内温度Ttin和室外温度Ttout的函数;PACmax为空调负荷电功率上限;QACmax为空调负荷制冷量上限;Tmax为设定温度舒适区的温度上限,具体见式(20)。室内外的温度差会消耗空调负荷虚拟储能储存的能量,令式(9)左侧等于0,可求得温度差消耗的功率Ptout为:
| $ P_t^{{\rm{out }}} = \frac{{{k_1}}}{{{k_2}}}\left[ {\frac{1}{{{R_1}}}\left( {T_t^{{\rm{out }}} - T_t^{{\rm{in }}}} \right) - \frac{{{k_1}{l_2} - {l_1}{k_2}}}{{{k_1}}}} \right] $ | (14) |
空调负荷群的虚拟储能模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {E_t^{{\rm{ACVB}}} = \sum\limits_{a = 1}^{{N_{\rm{AC}}}} {E_{a, t}^{{\rm{AC}}}} }\\ {P_t^{{\rm{ACVB}}} = \sum\limits_{a = 1}^{{N_{\rm{AC}}}} {\left( {P_{a, t}^{\rm{AC}} - P_{a, t}^{{\rm{out }}}} \right)} }\\ {E_t^{{\rm{ACVB}}} = E_{t - 1}^{\rm{ACVB}} + P_t^{\rm{ACVB}}\Delta t}\\ {E_t^{{\rm{ACVBmin}}} \le E_t^{\rm{ACVB}} \le E_t^{{\rm{ACVBmax}}}} \end{array}} \right. $ | (15) |
式中:EtACVB,PtACVB分别为t时刻空调负荷群的能量和功率;Ea, tAC,Pa, tAC分别为t时刻第a台空调负荷的能量和功率;Pa, tout为t时刻第a台空调负荷由温度差消耗的功率;EtACVBmax,EtACVBmin分别为t时刻空调负荷群最大能量和最小能量;NAC为空调负荷数量。
2.3 VPP虚拟储能模型VPP虚拟储能的模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {E_t^{{\rm{VPPVB}}} = E_t^{{\rm{EVVB}}} + E_t^{{\rm{ACVB }}}}\\ {P_t^{{\rm{VPPVB}}} = P_t^{{\rm{EVVB}}} + P_t^{{\rm{ACVB }}}}\\ {E_t^{{\rm{VPPVB}}} = E_{t - 1}^{{\rm{VPPB}}} + P_t^{{\rm{VPPVB}}}\Delta t}\\ {E_t^{{\rm{VPPVBmin}}} \le E_t^{{\rm{VPPVB}}} \le E_t^{{\rm{VPPVBmax}}}} \end{array}} \right. $ | (16) |
式中:EtVPPVB,PtVPPVB分别为t时刻VPP虚拟储能的能量和功率;EtVPPVBmax,EtVPPVBmin分别为VPP虚拟储能最大能量和最小能量,分别为电动汽车群虚拟储能与空调负荷群虚拟储能最大和最小能量之和。
3 日前优化调度模型在日前优化调度中,VPP按照历史运行数据预测日内的运行情况,包括电动汽车SOC和天气情况等,并以1 h为时间间隔将能量功率与调频容量相耦合,上报电力市场。调度模型以收益最大为目标,可参考式(6),其中调频里程可由历史数据预测得到。
3.1 电动汽车约束电动汽车SOC范围约束为:
| $ S_t^{\min } \le S_{k, t}^{{\rm{EV}}} \le S_t^{\max } $ | (17) |
式中:Stmax,Stmin分别为最大和最小SOC。
同时,为保障用户的出行需求,可设定每个时段的保底电量,使电动汽车离开电网时的电量不至于太低。
| $ S_t^{\min } = \frac{{{S^{{\rm{set }}}} - S}}{{{t^{{\rm{end }}}} - {t^{{\rm{str }}}}}}\left( {t - {t^{{\rm{str }}}}} \right) + S $ | (18) |
式中:Sset为用户设定出行时所需求的SOC;S为电动汽车初始SOC下限,文中取0.2;tstr为电动汽车接入电网的时刻;tend为电动汽车离开电网的时刻。
电动汽车的功率约束为:
| $ \left\{ {\begin{array}{*{20}{l}} {P_{k, t}^{{\rm{EV}}} + P_{k, i}^{{\rm{EVdn}}} \le {P^{{\rm{EVmax}}}}}\\ {P_{k, t}^{{\rm{EV}}} - P_{k, i}^{{\rm{EVup}}} \ge - {P^{{\rm{EVmax}}}}} \end{array}} \right. $ | (19) |
式中:PEVmax为电动汽车最大充放电功率;Pk, iEVup,Pk, iEVdn分别为i时段第k辆电动汽车的上调频容量和下调频容量。
3.2 空调负荷约束为保障用户的温度舒适度需求,定义温度舒适度区间,使室内温度维持在温度舒适度区间,故温度舒适度约束为:
| $ {T^{\min }} \le T_{a, t}^{{\rm{in }}} \le {T^{\max }} $ | (20) |
式中:Ta, tin为t时刻第a台空调负荷下的室内温度;Tmin为温度舒适区的温度下限。
空调负荷的功率约束为:
| $ \left\{ {\begin{array}{*{20}{l}} {P_{a, t}^{{\rm{AC}}} + P_{a, i}^{{\rm{ACdn}}} \le {P^{{\rm{ACmax}}}}}\\ {P_{a, t}^{{\rm{AC}}} - P_{a, i}^{{\rm{ACup}}} \ge {P^{{\rm{ACmin}}}}} \end{array}} \right. $ | (21) |
式中:PACmin为空调的最小功率;Pa, iACup,Pa, iACdn分别为i时段第a台空调负荷的上调频容量和下调频容量。
3.3 调频容量约束VPP参与市场的上、下调频容量需相同,即:
| $ \left\{ {\begin{array}{*{20}{l}} {P_i^{{\rm{VPPup}}} = \sum\limits_{k = 1}^{{N_{{\rm{EV}}}}} {P_{k, i}^{{\rm{EV up }}}} + \sum\limits_{a = 1}^{{N_{{\rm{AC }}}}} {P_{a, i}^{{\rm{Aup}}}} }\\ {P_i^{{\rm{VPPdn}}} = \sum\limits_{k = 1}^{{N_{{\rm{EV}}}}} {P_{k, i}^{{\rm{EVdn}}}} + \sum\limits_{a = 1}^{{N_{{\rm{AC }}}}} {P_{a, i}^{{\rm{ACdn}}}} }\\ {P_i^{{\rm{VPPup}}} = P_i^{{\rm{VPPdn}}}} \end{array}} \right. $ | (22) |
式中:PiVPPup,PiVPPdn分别为i时段VPP的上调频容量和下调频容量。
3.4 不确定性约束 3.4.1 调频信号不确定性分析采用累积单向需求系数(the rate of cumulative unidirectional demand,rCUD)[21]对调频信号进行分析。在上、下调频容量相等的情况下,rCUD为调频信号在时域上的积分。在一个时段内,rCUD与调频容量和时间的乘积即为这个时段需要响应的功率所对应的电量。
| $ {\chi _i} = \int_1^n {{\delta _t}} {\rm{d}}t $ | (23) |
式中:χi为i时段的rCUD。
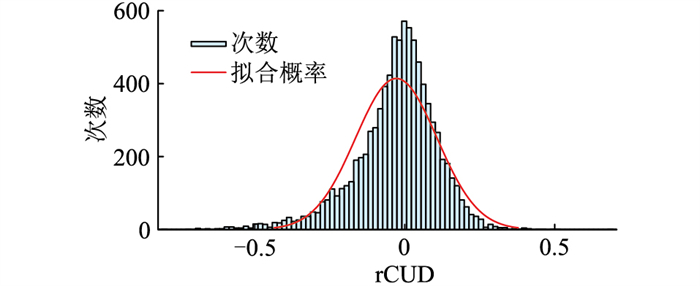
对PJM市场2020年全年8 784 h的调频信号进行分析,如图 3所示。可用正态分布对rCUD的概率分布进行拟合,即χi~N(μχ, σχ2)。其中,μχ=-0.028;σχ=0.136。
|
图 3 rCUD概率分布 Fig. 3 Probability distribution of rCUD |
在日前的优化调度中,考虑的不确定性有调频信号的不确定性、电动汽车到达时间和离开时间的不确定性、电动汽车初始电量的不确定性和气温预测的不确定性,假设以上误差均服从正态分布。
由于rCUD的分析是建立在上、下调频容量相等的情况下进行的,而单台电动汽车和空调负荷的上、下调频容量并不一定相等,如式(19)、式(21)所示。因此,需要对VPP整体的虚拟储能模型进行约束。
以一定置信水平将VPP虚拟储能的能量约束在上、下限之间:
| $ P\left( {E_t^{{\rm{VPPVBmin}}} \le E_t^{{\rm{VPPVB}}} \le E_t^{{\rm{VPPVBmax}}}} \right) \ge \alpha $ | (24) |
式中:α为置信水平;P(·)为满足约束的概率。
在随机变量均服从正态分布的情况下,式(24)可转化为[22]:
| $ \begin{array}{c} \sum\limits_{i = 1}^b {P_i^{\rm{E}}} + {\mu _\chi }\sum\limits_{i = 1}^b {P_i^{{\rm{FR}}}} - \sum\limits_{i = 1}^b {P_i^{{\rm{out }}}} + {\mathit{\Phi }^{ - 1}}(\alpha )\sqrt {{\sigma ^2}} \le \\ E_i^{{\rm{VPPVBmax}}} - {E^{{\rm{VPPVB0}}}} \end{array} $ | (25) |
| $ \begin{array}{c} \sum\limits_{i = 1}^b {P_i^{\rm{E}}} + {\mu _\chi }\sum\limits_{i = 1}^b {P_i^{{\rm{FR}}}} - \sum\limits_{i = 1}^b {P_i^{{\rm{out }}}} - {\mathit{\Phi }^{ - 1}}(\alpha )\sqrt {{\sigma ^2}} \ge \\ {E^{{\rm{VPPVB}}0}} - E_i^{{\rm{VPPVBmin}}} \end{array} $ | (26) |
| $ \begin{array}{c} {\sigma ^2} = \sum\limits_{i = 1}^b {\sigma _\chi ^2} {\left( {P_i^{{\rm{FR}}}} \right)^2} + \sigma _0^2 + \sum\limits_{i = 1}^b {{{\left( {\sigma _i^{{\rm{out}}}} \right)}^2}} + \\ {\left( {\sigma _i^{\max }} \right)^2} + {\left( {\sigma _i^{\min }} \right)^2} \end{array} $ | (27) |
式中:PiE为i时段VPP能量市场的竞标;PiFR为i时段调频容量的竞标;Piout为i时段空调负荷群由于温度差消耗的功率,其计算公式参照式(14);Φ-1(·)为正态累积分布函数的反函数;σ0为初始能量EVPPVB0的标准差;σiout为i时段温度差消耗功率的标准差;σimax,σimin分别为i时段虚拟储能上、下限EiVPPVBmax,EiVPPVBmin的标准差;b=1, 2, …, m。
方差计算公式如式(28)—式(31)所示。
| $ \sigma _0^2 = \frac{1}{4}\left( {N_{{\rm{EV}}}^2 + {N_{{\rm{EV}}}}} \right)\left( {E_0^2 + \sigma _{E0}^2} \right) - \frac{1}{4}N_{{\rm{EV}}}^2E_0^2 $ | (28) |
| $ {\left( {\sigma _i^{{\rm{out }}}} \right)^2} = \sum\limits_{a = 1}^{{N_{{\rm{AC}}}}} {{{\left( {\frac{{{k_1}}}{{{k_2}}} \cdot \frac{1}{{{R_{1, a}}}}} \right)}^2}} {\left( {\sigma _i^{{\rm{Tout }}}} \right)^2} $ | (29) |
| $ \begin{array}{c} {\left( {\sigma _i^{\max }} \right)^2} = {N_{{\rm{EV}}}}[\mathit{\Phi }(i)(1 - \mathit{\Phi }(i)) + \\ \mathit{\Phi }(i - m)(1 - \mathit{\Phi }(i - m))]{\left( {E_i^{{\rm{VPPVBmax}}}} \right)^2} \end{array} $ | (30) |
| $ \begin{array}{c} {\left( {\sigma _i^{\min }} \right)^2} = {N_{{\rm{EV}}}}[\mathit{\Phi }(i)(1 - \mathit{\Phi }(i)) + \\ \mathit{\Phi }(i - m)(1 - \mathit{\Phi }(i - m))]{\left( {E_i^{{\rm{VPPVBmin}}}} \right)^2} \end{array} $ | (31) |
式中:E0,σE0分别为电动汽车到达时电量的期望和标准差;R1, a为第a台空调负荷的等效阻抗;σiTout为i时段室外温度的标准差。
4 实时优化调度模型在实时调度中,VPP响应能量出力,同时响应调度中心向VPP下发的调频信号,时间粒度为2 s。VPP集中控制器实时接收调频信号并计算整体需要响应的功率,之后确认电动汽车和空调负荷的运行状态,并改变各电动汽车和空调负荷的接入功率,以满足用能需求和系统的调频需求。在分配功率时,需要最小化VPP的成本。将成本目标函数分为三部分,即信号跟踪效果成本、用户需求成本和用能成本。
(1) 信号跟踪效果成本。
| $ {C_1} = \varepsilon \left| {P_t^{{\rm{RR}}} - P_t^{{\rm{FR}}}} \right| $ | (32) |
式中:ε为误差成本转化系数。
(2) 用户需求成本。
| $ \begin{array}{c} {C_2} = {\varepsilon _{{\rm{EV}}}}\sum\limits_{k = 1}^{{N_{{\rm{EV}}}}} {\left| {S_{k, t}^{{\rm{EV}}} - S_t^{\max }} \right|} + \\ {\varepsilon _{{\rm{AC}}}}\sum\limits_{a = 1}^{{N_{{\rm{AC}}}}} {{{\left| {T_{a, t}^{{\rm{in }}} - \left( {{T^{\max }} + {T^{\min }}} \right)/2} \right|}^2}} \end{array} $ | (33) |
式中:εEV为电动汽车需求成本转化系数;εAC为空调负荷需求成本转化系数。
(3) 用能成本。空调负荷的用能成本为[11]:
| $ C_a^{{\rm{AC}}} = {a_{{\rm{AC}}}}{\left( {P_{a, t}^{{\rm{AC}}}} \right)^2} + {b_{{\rm{AC}}}}P_{a, t}^{{\rm{AC}}} + {c_{{\rm{AC}}}} $ | (34) |
式中:aAC,bAC,cAC为空调负荷用能成本系数。
电动汽车放电会缩短电池的寿命,因此对每次放电,采用线性函数定义电动汽车的成本。电动汽车的用能成本为[23]:
| $ C_k^{{\rm{EV}}} = {a_{{\rm{EV}}}}\left( {P_{k, t}^{{\rm{EV}}} + \left| {P_{k, t}^{{\rm{EV}}}} \right|} \right)/2 $ | (35) |
式中:aEV为电动汽车用能成本系数。
则VPP的用能成本为:
| $ {C_3} = \sum\limits_{a = 1}^{{N_{{\rm{AC}}}}} {C_a^{{\rm{AC}}}} + \sum\limits_{k = 1}^{{N_{{\rm{EV}}}}} {C_k^{{\rm{EV}}}} $ | (36) |
在实时的优化调度中,约束条件包含电动汽车的SOC范围约束和功率约束、空调负荷的功率约束和温度舒适度约束。
综上所述,日内的优化调度模型可写为:
| $ \left\{ {\begin{array}{*{20}{l}} {f = }&{\min \left( {\omega {C_1} + \xi {C_2} + \psi {C_3}} \right)}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}}&{S_t^{\min } \le S_{k, t}^{{\rm{EV}}} \le S_t^{\max }}\\ {}&{ - {P^{{\rm{EVmax}}}} \le P_{k, t}^{{\rm{EV}}} \le {P^{{\rm{EVmax}}}}}\\ {}&{{P^{{\rm{ACmin}}}} \le P_{a, t}^{{\rm{AC}}} \le {P^{{\rm{ACmax}}}}}\\ {}&{{T^{\min }} \le T_{a, t}^{{\rm{in}}} \le {T^{\max }}} \end{array}} \right. $ | (37) |
式中:ω,ξ,ψ分别为C1,C2,C3这3种成本的权重因子。在实时调度中,可根据实际需求调节3种成本的比重,以应对需求侧的不确定性和用电需求。
5 算例分析文中选取夏季市区内将空调负荷和电动汽车作为灵活性调频资源的楼宇型VPP互联集群为研究对象,其平均规模包括100台电动汽车和100台变频空调。假设用户08:00上班,17:00下班,即电动汽车接入电网和使用空调的时间段为08:00—17:00。采用蒙特卡洛法按正态分布初始化灵活资源的接入信息,包括电动汽车初始SOC、电动汽车到达与离开时间、建筑等效参数等。其中电动汽车相关参数参考文献[18],空调负荷相关参数参考文献[20],市场价格和调频信号数据参考PJM市场历史数据。假设负荷群内的所有电动汽车和空调均满足功率和容量的约束条件,且不考虑电池老化、温度变化对参数的影响。取机会约束规划的置信系数α为0.95;误差成本转化系数ε为5 000;电动汽车需求成本转化系数εEV为50;空调负荷需求成本转化系数εAC为2 000;空调负荷用能成本系数参考文献[11];电动汽车用能成本参考文献[23]。3种成本的权重因子均取1。在Matlab中调用Gurobi求解器对上述优化调度模型进行求解。
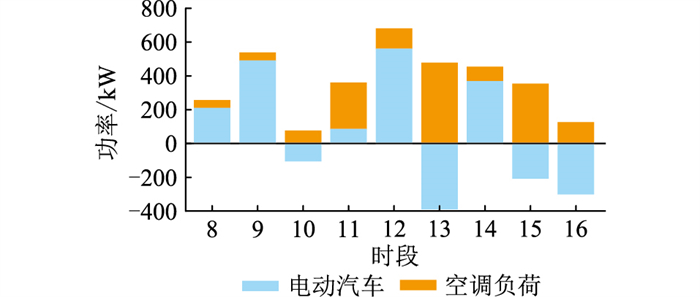
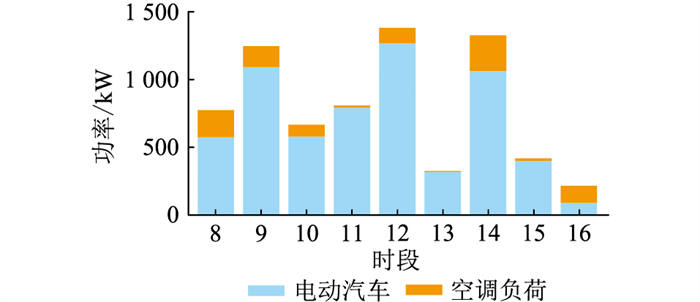
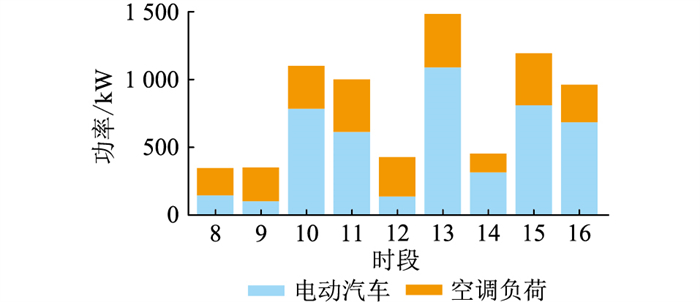
5.1 日前优化调度结果VPP在日前能量市场的调度结果如图 4所示,上调频容量如图 5所示,下调频容量如图 6所示。
|
图 4 日前能量市场 Fig. 4 Day-ahead energy market |
|
图 5 日前上调频容量 Fig. 5 Day-ahead up regulation capacity |
|
图 6 日前下调频容量 Fig. 6 Day-ahead down regulation capacity |
在能量市场方面,电动汽车和空调负荷的联合调度也能起到互补的作用,在电价较低时利用虚拟储能存储能量,并在电量较高时售出。同时,空调负荷利用建筑的储热效应能减小电动汽车出行不确定性带来的影响。
在调频市场方面,电动汽车和空调负荷的联合调度能起到互补的作用。由于需要保障用户的出行需求,电动汽车需要保证平均充电功率在一定水平之上,所以上调频容量较大,而下调频容量较小。相对应地,在室内外温度差较小时,空调负荷的功率较小,也就是上调频容量较小,而下调频容量较大。两者结合使得VPP的上、下调频容量差更小,在调频市场的收益更高。
不同场景下VPP日前收益如表 1所示。电动汽车和空调负荷联合调度时总收益为388.3元,而两者分别调度时总收益相加的结果为278元。相比之下,联合调度能使VPP的总收益提高39.68%。联合调度既降低了VPP的电量成本,也提高了调频收益,体现了2种负荷聚合后的相互支撑作用。
|
|
表 1 VPP日前收益 Table 1 Day-ahead revenue of VPP |
不同置信水平下VPP日前收益如表 2所示。随着置信水平的减小,电量成本降低,调频收益增加,VPP的总收益增大,这意味着VPP更倾向于参加调频市场而不是能量市场。这是由于置信水平减小,日前对调频信号不确定性的约束也就越小,因此可更多地参与调频市场。
|
|
表 2 不同置信水平下VPP日前收益 Table 2 Day-ahead revenue of VPP in different confidence levels |
在日内实时优化调度中,每个调度周期优化计算用时为0.18 s,远小于调频信号的时间粒度2 s,验证了实时控制的可行性。
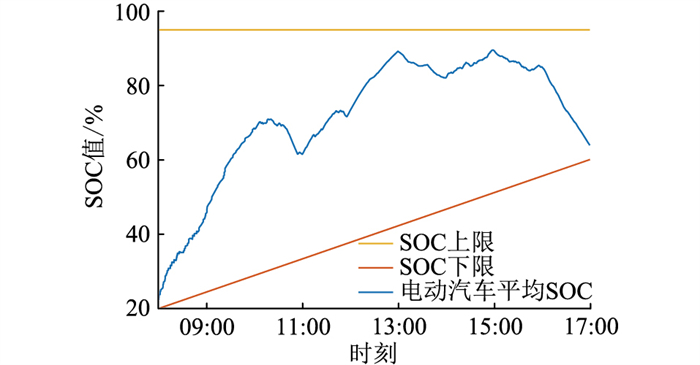
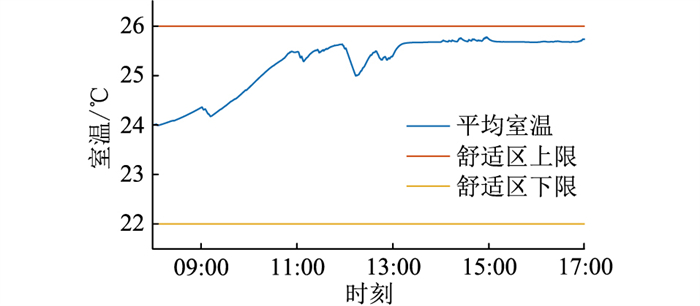
电动汽车平均SOC见图 7,平均室温见图 8。可知电动汽车平均SOC较好地保持在所设定的上、下限内,室内温度也能维持在温度舒适区内。在调度初期,空调负荷减小制冷功率,同时电动汽车快速充电,将能量储存在电动汽车虚拟储能中,保障了电动汽车的充电速率。在调度末期,由于此时室内温度较高,为响应电网需求,进入电动汽车入网状态,保证室温在温度舒适区内。说明2种负荷的联合调度起到相互支撑的作用,同时在实时功率的分配中考虑用户的温度舒适度需求多于出行需求。
|
图 7 电动汽车平均SOC Fig. 7 Average SOC of EVs |
|
图 8 平均室温 Fig. 8 Average indoor temperature |
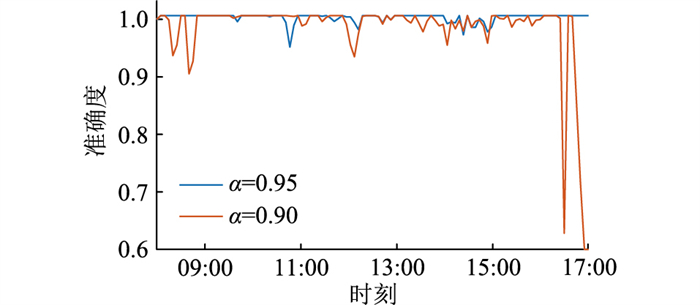
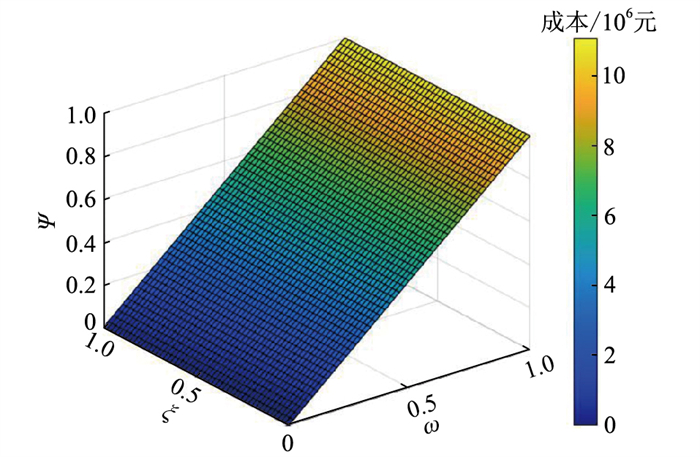
日内调频准确度指标如图 9所示。可以看出在大部分时间内,当α=0.95时调频准确度均在0.95以上,而当α=0.90时调频准确度相对降低。这说明提高机会约束的置信水平能有效提高VPP调频准确度。某一时刻实时成本与成本权重系数的关系如图 10所示,可以看出,不同参数对于VPP的成本影响程度也存在差异。在本算例的设置中,信号跟踪效果成本对总体成本的影响最为明显,因此优先考虑提高调频的准确度。同时,用户需求成本系数可根据用户的需求进行调整,在用户需求比较迫切时增大需求成本系数,可令VPP在实时调度中优先满足用户需求。
|
图 9 调频准确度 Fig. 9 Frequency regulation accuracy |
|
图 10 成本与权重系数的关系 Fig. 10 Relationship between cost and weight coefficient |
综上所述,联合调度智能楼宇中的电动汽车和空调负荷能在功率上起到相互支撑的作用,参与调频服务市场能在满足用户需求的基础上有效响应电力系统的调频信号,并具备较高的准确性,降低了智能楼宇运行的成本。
6 结论为充分利用智能楼宇中的需求侧资源,文中提出了智能楼宇型VPP参与系统调频辅助服务控制策略,建立需求侧资源的虚拟储能模型,在日前将调频信号与用户侧的不确定性纳入考量,在日内以成本最优实现优化调度。主要得出以下结论:
(1) 基于机会约束规划的日前不确定性规划可以减小调频信号不确定性的影响,提升智能楼宇型VPP日内调频的准确度。
(2) 通过建立智能楼宇中的电动汽车和空调负荷的虚拟储能模型,并进行联合调度,能耦合智能楼宇用电功率与调频容量,使2种负荷相互支撑,提升智能楼宇运行效益。
| [1] |
徐青山, 王栋, 戴蔚莺, 等. 变频空调负荷虚拟同步机化改造及其参与微网互动调控[J]. 电力自动化设备, 2020, 40(3): 8-14. XU Qingshan, WANG Dong, DAI Weiying, et al. Virtual synchronous machine transformation of inverter air conditioning load and its participation in microgrid interactive control[J]. Electric Power Automation Equipment, 2020, 40(3): 8-14. (  0) 0) |
| [2] |
殷爽睿, 艾芊, 王大鹏, 等. 考虑空调负荷虚拟储能的产消者鲁棒日前申报策略[J]. 电力系统自动化, 2020, 44(4): 24-34. YIN Shuangrui, AI Qian, WANG Dapeng, et al. Day-ahead robust bidding strategy for prosumer considering virtual energy storage of air-conditioning load[J]. Automation of Electric Power Systems, 2020, 44(4): 24-34. (  0) 0) |
| [3] |
LIU H, QI J J, WANG J H, et al. EV dispatch control for supplementary frequency regulation considering the expectation of EV owners[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3763-3772. DOI:10.1109/TSG.2016.2641481 (  0) 0) |
| [4] |
WANG M S, MU Y F, SHI Q X, et al. Electric vehicle aggregator modeling and control for frequency regulation considering progressive state recovery[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 4176-4189. DOI:10.1109/TSG.2020.2981843 (  0) 0) |
| [5] |
王旭东, 吴莉萍, 戚艳, 等. 基于模型预测控制的智能楼宇暖通空调能量管理策略[J]. 电力系统及其自动化学报, 2019, 31(6): 98-106. WANG Xudong, WU Liping, QI Yan, et al. Energy management strategy for heating, ventilation and air conditioning in smart building based on model predictive control[J]. Proceedings of the CSU-EPSA, 2019, 31(6): 98-106. (  0) 0) |
| [6] |
贾雨龙, 米增强, 王俊杰, 等. 柔性负荷聚合商参与电力系统的多时间尺度协同优化调度策略[J]. 华北电力大学学报(自然科学版), 2019, 46(6): 17-26. JIA Yulong, MI Zengqiang, WANG Junjie, et al. Mutli-time scale collaborative optimal scheduling strategy with flexible load aggregator participating in power system[J]. Journal of North China Electric Power University (Natural Science Edition), 2019, 46(6): 17-26. (  0) 0) |
| [7] |
陈雯, 孙荣峰, 邱靖, 等. 考虑电池寿命的虚拟电厂调频竞标模型及合作利润分配策略[J]. 全球能源互联网, 2020, 3(4): 374-384. CHEN Wen, SUN Rongfeng, QIU Jing, et al. Profit allocation and frequency regulation bidding strategy of virtual power plant considering battery cycle life[J]. Journal of Global Energy Interconnection, 2020, 3(4): 374-384. DOI:10.19705/j.cnki.issn2096-5125.2020.04.006 (  0) 0) |
| [8] |
KWON M, CHOI S. An electrolytic capacitorless bidirectional EV charger for V2G and V2H applications[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 6792-6799. (  0) 0) |
| [9] |
KIM Y J, FUENTES E, NORFORD L K. Experimental study of grid frequency regulation ancillary service of a variable speed heat pump[J]. IEEE Transactions on Power Systems, 2016, 31(4): 3090-3099. (  0) 0) |
| [10] |
WENZEL G, NEGRETE-PINCETIC M, OLIVARES D E, et al. Real-time charging strategies for an electric vehicle aggregator to provide ancillary services[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5141-5151. (  0) 0) |
| [11] |
HU J Q, CAO J D, YONG T Y, et al. Demand response load following of source and load systems[J]. IEEE Transactions on Control Systems Technology, 2017, 25(5): 1586-1598. (  0) 0) |
| [12] |
吴洲洋, 艾欣, 胡俊杰, 等. 基于充电行为预测的电动汽车参与系统调频备用: 容量挖掘与风险评估[J]. 电力自动化设备, 2022, 42(4): 18-26. WU Zhouyang, AI Xin, HU Junjie, et al. EVs' participation in system frequency regulation reserve based on charging behavior prediction: capacity mining and risk evaluation[J]. Electric Power Automation Equipment, 2022, 42(4): 18-26. (  0) 0) |
| [13] |
YAO E X, WONG V W S, SCHOBER R. Robust frequency regulation capacity scheduling algorithm for electric vehicles[J]. IEEE Transactions on Smart Grid, 2017, 8(2): 984-997. (  0) 0) |
| [14] |
文艺林, 胡泽春, 宁剑, 等. 基于分布鲁棒机会约束的充电运营商参与调峰市场投标策略[J]. 电力系统自动化, 2022, 46(7): 23-32. WEN Yilin, HU Zechun, NING Jian, et al. Bidding strategy of charging operator participating in peak regulation market based on distributionally robust chance constraint[J]. Automation of Electric Power Systems, 2022, 46(7): 23-32. (  0) 0) |
| [15] |
ANSARI M, AL-AWAMI A T, SORTOMME E, et al. Coordinated bidding of ancillary services for vehicle-to-grid using fuzzy optimization[J]. IEEE Transactions on Smart Grid, 2015, 6(1): 261-270. (  0) 0) |
| [16] |
吴洲洋, 艾欣, 胡俊杰. 需求侧灵活性资源参与调频辅助服务的备用优化与实时调度[J]. 电力系统自动化, 2021, 45(6): 148-157. WU Zhouyang, AI Xin, HU Junjie. Reserve optimization and real-time scheduling of frequency regulation ancillary service with participation of flexible resource on demand side[J]. Automation of Electric Power Systems, 2021, 45(6): 148-157. (  0) 0) |
| [17] |
屈富敏, 赵健, 蔡帜, 等. 电动汽车与温控负荷虚拟电厂协同优化控制策略[J]. 电力系统及其自动化学报, 2021, 33(1): 48-56. QU Fumin, ZHAO Jian, CAI Zhi, et al. Coordinated optimal control strategy for electric vehicle and thermostatically-controlled load aggregators[J]. Proceedings of the CSU-EPSA, 2021, 33(1): 48-56. (  0) 0) |
| [18] |
杨铮, 彭思成, 廖清芬, 等. 面向综合能源楼宇的电动汽车辅助服务方案[J]. 电网技术, 2017, 41(9): 2831-2843. YANG Zheng, PENG Sicheng, LIAO Qingfen, et al. Ancillary services provided by electric vehicles for building integrated energy system[J]. Power System Technology, 2017, 41(9): 2831-2843. (  0) 0) |
| [19] |
WU J C, HU J J, AI X, et al. Multi-time scale energy management of electric vehicle model-based prosumers by using virtual battery model[J]. Applied Energy, 2019, 251: 113312. (  0) 0) |
| [20] |
SONG M, GAO C W, YAN H G, et al. Thermal battery modeling of inverter air conditioning for demand response[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 5522-5534. (  0) 0) |
| [21] |
AI X, WU Z Y, HU J J, et al. Robust operation strategy enabling a combined wind/battery power plant for providing energy and frequency ancillary services[J]. International Journal of Electrical Power & Energy Systems, 2020, 118: 105736. (  0) 0) |
| [22] |
WU H Y, SHAHIDEHPOUR M, LI Z Y, et al. Chance-constrained day-ahead scheduling in stochastic power system operation[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1583-1591. (  0) 0) |
| [23] |
BORDIN C, ANUTA H O, CROSSLAND A, et al. A linear programming approach for battery degradation analysis and optimization in offgrid power systems with solar energy integration[J]. Renewable Energy, 2017, 101: 417-430. (  0) 0) |
2. State Grid Pudong Power Supply Company, SMEPC, Shanghai 200120, China;
3. State Grid Shanghai Municipal Electric Power Company, Shanghai 200122, China

 湛归(1999), 男, 硕士在读, 研究方向为虚拟电厂优化运行(E-mail:
湛归(1999), 男, 硕士在读, 研究方向为虚拟电厂优化运行(E-mail: