文章编号: 2096-3203(2022)04-0091-09 中图分类号: TM73
2. 能源互联网供需运营湖南省重点实验室, 湖南 长沙 410004;
3. 长沙理工大学电气与信息工程学院, 湖南 长沙 410114
《电力中长期交易基本规则(暂行)》[1](简称《规则》)发布后,现阶段我国电力中长期交易市场已逐步形成并完善[2-4],多省电力市场进入以中长期电量交易为主的市场过渡期[5-6]。在中长期电量交易中,不确定的电源出力、用电负荷等将导致购售电双方实际发用电量与签订的中长期合约电量出现偏差,对此《规则》中建议采用预挂牌月偏差平衡的合同偏差处理机制。
预挂牌月偏差平衡方式加强了月度合同刚性执行力度[7],对调度方法要求高。为适应该偏差平衡机制,须寻求一种合适的调度方法,一方面能减小系统偏差平衡成本,另一方面可确保中长期交易结果的有效性以及对各市场主体的调度公平性[8]。
目前我国电力系统采用的调度方法主要有公平性调度[9-10]、节能调度[11-13]和经济调度[14-16]等,电力市场环境下主要研究现货市场下的短期调度[17-21],仅少数文献研究了电力市场过渡期系统调度方法。文献[22]以日为粒度构建了以电量完成偏差与开机成本之和最小为目标的月度机组组合模型,实现日时间尺度上中长期交易和发电计划的协调优化。然而由于负荷预测精度、可再生能源不确定性等影响,由月度机组组合模型得到的中长期交易日计划电量在实际日调度计划中难以执行,执行难度随时间的推进逐渐增加。文献[23]提出含月合约电量分解、周优化调度和日前优化调度的滚动协调调度模式,一定程度上弥补了文献[22]的不足。文献[24]提出基于电量分解的市场过渡期水火电短期联合调度模型,调节非市场机组电量处理偏差电量,实现机组合约偏差电量最小。上述文献多致力于减小机组合约执行偏差,但由于传统偏差处理手段无独立的偏差结算价格,已有研究未考虑处理机组合约执行偏差的经济性,难以适应预挂牌月偏差平衡方式处理偏差电量的情况。文献[25]在预招标月度偏差平衡机制下,建立从月度预发电计划滚动修正、日前电量分解及发电计划优化到日内实时电力平衡的多周期发电调度优化模型,虽可实现月度偏差电量调整成本的最小化,但未考虑火电、风电、水电等多类机组的协调优化关系,忽略了系统内水电的复杂运行约束,难以满足实际工程需求。
为在预挂牌月偏差平衡机制下降低偏差电量平衡成本,得到合理有效的中长期交易结果,文中提出机组偏差电量月内滚动的含水火风电系统月度调度方法。提出基于火电机组合约完成进度公平性的月度火电合约电量分解模型,以偏差电量平衡成本、火电机组煤耗和水电机组弃水最小为目标建立含水火风电系统日前调度模型,日内调度按清洁能源优先发电,火电机组上下调成本最低的原则安排出力。算例仿真表明所提调度方法充分利用了清洁能源发电,减少了火电机组月度电量偏差,实现了偏差电量平衡成本最小化,可为市场过渡期的系统调度提供决策支持。
1 偏差电量月内滚动调度法预挂牌月偏差平衡机制是指在电源侧形成统一的偏差电量结算价格,即在月前通过组织发电商参与预挂牌交易,确定机组参与月度上调或者下调的电量调整报价。当用户实际用电量大于或小于合约电量时,安排电源侧以上调或下调价格由低到高的顺序调用机组增发或者减发,以实现源荷两侧电力电量平衡[7]。
为实现交易月结月清,预挂牌月偏差平衡机制规定以月为周期进行交易与结算,年度合同电量须明确分解到月,并按月执行,原则上未完成的月度计划电量不能滚动到后续月份执行。月底结算时机组实际上网电量超出合约部分结算为上调电量,少于合约部分结算为下调电量[7]。
由此,预挂牌偏差处理机制旨在通过调整电源侧出力确保供需平衡,并通过价格机制解耦发用双方的电量结算,以实现在对发电商进行结算时不用考虑其代理用户实际用电情况,简化结算流程。
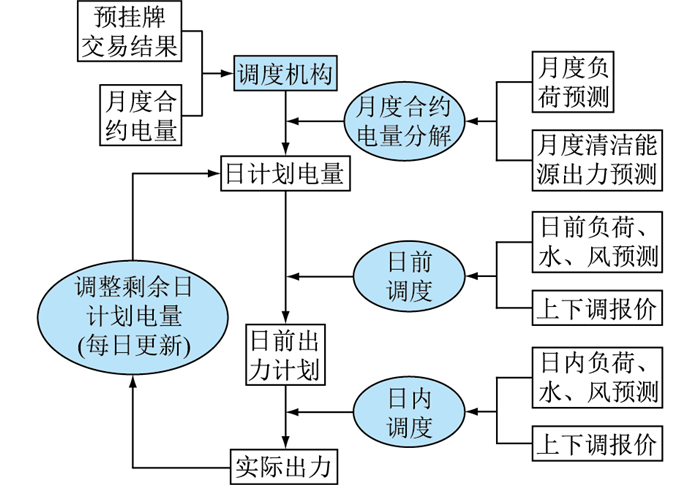
预挂牌月偏差平衡方式加强了月度合同刚性执行力度,尤其在清洁能源占比较大的地区,亟需找出一种与这种偏差平衡机制相适应的、经济有效的调度方法。由此,文中针对预挂牌月偏差平衡机制下含水火风电系统调度问题,提出偏差电量月内滚动调度方法,如图 1所示。其中,为确保清洁能源可以得到充分利用,水电机组和风电机组不参与月度偏差电量调整,仅火电机组参与预挂牌交易。
|
图 1 偏差电量月内滚动调度方法 Fig. 1 Monthly dispatch method of rolling unbalanced electric quantity |
(1) 月度合约电量分解。当得到交易中心提供的该月各机组月度合约电量(包括月度合同电量和月度基数电量)以及机组调整报价后,调度机构要根据清洁能源出力预测、负荷预测等公平地将各机组的月度电量分解到各日作为初始日计划电量。
(2) 日前、日内调度。在每个调度日前基于火电机组日计划电量、上下调价格和日前负荷、水、风预测制定日前机组出力计划;调度日当天各时段负荷、水、风情况与日前预测之间的偏差,按火电机组调整报价排序安排机组实时调整出力。
(3) 偏差电量月内滚动。日调度结束后要统计出各火电机组该日实际发电量和日计划发电量之间的偏差情况,将该日偏差电量平均分摊到剩余每日的计划电量。当以这种方法进行到该月的最后一日调度完成时,最后一日火电机组的实发电量和该日机组的计划电量的差就等于该机组的月度总偏差电量,调度机构再根据机组上下调价低优先原则安排机组出力,则可以实现月偏差平衡费用最小。
2 月度合约电量分解模型偏差电量月内滚动调度方法的基础和前提是月度合约电量分解,在该月第一个调度日来临之前,须将月度合约电量分解到日,以确定该月每天各火电机组的初始日计划发电量。
火电的合约电量分解参考文献[24]中的电量分解二次规划法,以各机组的合约完成进度偏差f0最小为目标。
| $\min f_{0} =\sum\limits_{x=1}^{X}\left[\frac{1}{I} \sum\limits_{i=1}^{I}\left(c_{i, x}-\bar{c}_{x}\right)^{2}\right] $ | (1) |
| $c_{i, x} =\frac{E_{i, x}^{\mathrm{F}}+E_{i, x-1}^{\mathrm{F}, \mathrm{e}}}{E_{i, \mathrm{mon}}^{\mathrm{F}} \times 100 \%} $ | (2) |
| $ \bar{c}_{x} =\frac{1}{I} \sum\limits_{i=1}^{I} c_{i, x} \times 100 \% $ | (3) |
| $ E_{i, x-1}^{\mathrm{F}, \mathrm{e}}=\sum\limits_{d=1}^{x-1} E_{i, d}^{\mathrm{F}} $ | (4) |
式中:I,X分别为火电机组总数和总天数;
| $ \begin{gathered} E_{i, x}^{\mathrm{F}, \min } \leqslant E_{i, x}^{\mathrm{F}} \leqslant E_{i, x}^{\mathrm{F}, \max } \end{gathered} $ | (5) |
| $ \sum\limits_{x=1}^{X} E_{i, x}^{\mathrm{F}}=E_{i, \operatorname{mon}}^{\mathrm{F}} $ | (6) |
| $ \begin{gathered} \sum\limits_{i=1}^{I} E_{i, x}^{\mathrm{F}}+\sum\limits_{j=1}^{J} E_{j, x}^{\mathrm{H}}+\sum\limits_{k=1}^{K} E_{k, x}^{\mathrm{W}}= \\ D_{x} \times \frac{\sum\limits_{i=1}^{I} E_{i, \text { mon }}^{\mathrm{F}}+\sum\limits_{j=1}^{J} E_{j, \mathrm{mon}}^{\mathrm{H}}+\sum\limits_{k=1}^{K} E_{k, \text { mon }}^{\mathrm{W}}}{\sum\limits_{x=1}^{X} D_{x}} \end{gathered} $ | (7) |
式中: Dx为第x天的负荷需求预测;Ei, xF, min,Ei, xF, max分别为火电机组i第x天分配电量的最小、最大值;J,K分别为系统水电、风电机组总数;Ej, xH,Ej, monH分别为水电机组j在第x天的预测电量和月度总电量;Ek, xW,Ek, monW分别为风电机组k在第x天的预测电量和月度总电量,可以通过历史同期数据预测得到。式(5)-式(7)分别为各机组日分解电量上下限约束、总合约电量约束以及日机组总发电量约束。
由该模型可以得到各机组初始日计划电量,是进行月度调度的前提。
3 偏差电量月内滚动法日调度模型 3.1 含偏差平衡成本目标日前调度模型因为购电成本在与发电侧签订中长期购电合同时已经确定,所以日前调度优化目标不考虑购电成本,而仅考虑偏差平衡成本和节能降耗。日前调度思路为:在日前负荷、水、风预测的基础上,风电优先出力,具有一定调节库容的水电在保证弃水最小的前提下尽可能多发,并在一定程度上分担火电机组的调整电量,火电机组出力同时考虑偏差电量平衡费用和煤耗,由此建立日前调度模型。
3.1.1 目标函数(1) 偏差平衡成本。日调度应以最经济的方式尽量使机组出力与日计划电量偏差最小,由此设立目标函数为:
| $\begin{gathered} \min f_{1}=\sum\limits_{u=1}^{N_{\text {inc }}}\left(E_{u}-E_{u, \text { day }}\right) C_{u, \text { inc }}+ \\ \sum\limits_{v=1}^{N_{\mathrm{dec}}}\left(E_{v, \mathrm{day}}-E_{v}\right) C_{v, \mathrm{dec}} \end{gathered} $ | (8) |
式中:Ninc,Ndec分别为参与上调和下调的机组数;Eu,Ev分别为上调机组u和下调机组v日实发电量;Eu, day,Ev, day分别为上调机组u和下调机组v日计划电量;Cu, inc,Cv, dec分别为上调机组u的上调报价和下调机组v的下调报价。
(2) 节能降耗目标。根据节能减排政策要求,在制定机组出力计划时应考虑系统火电煤耗水平,火电煤耗为:
| $ f_{\mathrm{F}}=\sum\limits_{t=1}^{T} \sum\limits_{i=1}^{I}\left[\left(a_{i} P_{i, t}^{2}+b_{i} P_{i, t}+c_{i} \delta_{i, t}\right)+S_{i, t}^{\mathrm{U}}+S_{i, t}^{\mathrm{D}}\right] $ | (9) |
式中:ai,bi,ci为火电机组i的煤耗系数;δi, t为火电机组i在t时刻的启停状态,为0-1变量;Pi, t为火电机组i在t时刻的出力;t∈T,T为调度周期,即1 d;Si, tU,Si, tD分别为火电机组i在t时刻的启、停煤耗。
为充分利用水资源,减少水能资源浪费,设置水电机组弃水成本,用弃水体积折算为煤耗表示:
| $ f_{\mathrm{H}}=\sum\limits_{t=1}^{T} \sum\limits_{j=1}^{J} 3600 \eta d_{j, t} $ | (10) |
式中:dj, t为水电机组j在t时刻的弃水流量;η为水煤折算系数。
风电机组弃风为:
| $ f_{\mathrm{W}}=\sum\limits_{t=1}^{T} \sum\limits_{k=1}^{K} \gamma\left(P_{k, \max }-P_{k, t}\right) $ | (11) |
式中:Pk, t,Pk, max分别为t时刻风电机组k出力和最大预测出力;γ为折算系数。
综上,节能降耗目标函数为:
| $ \min f_{2}=f_{\mathrm{F}}+f_{\mathrm{H}}+f_{\mathrm{W}} $ | (12) |
(1) 节点功率平衡。
| $ \sum\limits_{g \in G_{n}} P_{g, t}-P_{\mathrm{L}, n, t}=\sum\limits_{n b \in M} F_{n b, t}-\sum\limits_{a n \in M} F_{a n, t} $ | (13) |
式中:M,Gn分别为总支路数和接入节点n的机组数;Pg, t,PL, n, t分别为t时刻节点n的发电功率和负荷功率;Fnb, t,Fan, t分别为t时刻支路nb、an的功率潮流。
(2) 备用约束。
| $ \sum\limits_{i=1}^{I} P_{i, \max } \delta_{i, t}+\sum\limits_{j=1}^{J} P_{j, t, \max }-\sum\limits_{l=1}^{L} P_{l, t} \geqslant S $ | (14) |
式中:Pi, max,Pj, t, max,Pl, t分别为火电机组i、水电机组j在t时刻最大可用出力和t时刻节点l的负荷;L为系统内负荷节点数量;S为备用要求。
(3) 线路传输约束。
| $ F_{n b, t}=\left(\theta_{p}-\theta_{q}\right) / x_{p q} \quad p, q \in n $ | (15) |
| $ F_{\min } \leqslant F_{n b, t} \leqslant F_{\max } $ | (16) |
| $ \theta_{p \min } \leqslant \theta_{p, t} \leqslant \theta_{p \max } $ | (17) |
| $\theta_{\text {ref }}=0 $ | (18) |
式中:Fmax,Fmin分别为支路nb潮流功率上、下限;θp,θq,xpq分别为支路两端节点的相角以及支路电抗;θp, t,θp, max,θp, min分别为节点p在t时刻的相角和相角上、下限(±360°);θref为平衡节点相角。式(15)-式(18)分别为线路传输功率约束、传输功率上下限约束、节点电压相角约束和平衡节点相角约束。
(4) 火电机组约束。
| $ \delta_{i, t} P_{i, \min } \leqslant P_{i, t} \leqslant \delta_{i, t} P_{i, \max } $ | (19) |
| $\left\{\begin{array}{l} P_{i, t}-P_{i, t-1} \leqslant R_{\mathrm{U}_{i}} \delta_{i, t-1}+ \\ \quad P_{i, \min }\left(\delta_{i, t}-\delta_{i, t-1}\right)+P_{i, \max }\left(1-\delta_{i, t}\right) \\ P_{i, t-1}-P_{i, t} \leqslant R_{\mathrm{D}_{i}} \delta_{i, t}+ \\ \quad P_{i, \min }\left(\delta_{i, t-1}-\delta_{i, t}\right)+P_{i, \max }\left(1-\delta_{i, t-1}\right) \end{array}\right. $ | (20) |
| $ \left\{\begin{array}{l} \left(X_{i, t-1}^{\mathrm{on}}-T_{i, t}^{\mathrm{on}}\right)\left(\delta_{i, t-1}-\delta_{i, t}\right) \geqslant 0 \\ \left(X_{i, t-1}^{\mathrm{off}}-T_{i, t}^{\mathrm{off}}\right)\left(\delta_{i, t}-\delta_{i, t-1}\right) \geqslant 0 \end{array}\right. $ | (21) |
式中:Pi, max,Pi, min分别为火电机组i出力上、下限;RUi,RDi为机组爬坡限制;Xi, t-1on,Xi, t-1off分别为机组持续运行和停机时间;Ti, ton,Ti, toff分别为机组允许最小运行和停机时间。式(19)-式(21)分别为火电机组出力限制、爬坡约束、最小停机和运行时间约束。
(5) 水电机组约束。
| $ V_{j, t}=V_{j, t-1}+3600\left(q_{j, t}^{\text {in }}-q_{j, t}-d_{j, t}\right) $ | (22) |
| $ V_{j, \min } \leqslant V_{j, t} \leqslant V_{j, \max } $ | (23) |
| $ 0 \leqslant q_{j, t} \leqslant q_{j, \max } $ | (24) |
| $ 0 \leqslant P_{j, t} \leqslant P_{j, \max } $ | (25) |
| $q_{j, t}=P_{j, t} \rho_{j} / 3600 $ | (26) |
式中:Vj, t为水电机组j在t时刻的库容;Vj, max,Vj, min分别为水电机组j的库容上、下限;qj, tin,qj, t分别为t时刻入库和发电流量;qj, max为水电机组j发电容量上限;Pj, t,Pj, max分别为水电机组j在t时刻的出力和最大出力;ρj为水电机组j的发电耗水率[26]。式(22)-式(26)分别为水电机组流量平衡约束、库容上下限、发电流量约束、出力约束以及发电流量和机组出力关系。
(6) 风电机组约束。
| $ 0 \leqslant P_{k, t} \leqslant P_{k, \max } $ | (27) |
日内调度即在调度日内对日前调度计划的调整,以适应实际负荷、来水、来风的情况。日内调度的思路为:风电机组优先出力,水电机组在保证弃水最小的情况下首先参与调节,随后火电机组不改变原有机组组合计划,按各机组上下调报价排序安排机组调整出力,以保证日内实时调整的经济性,由此建立日内调度模型。
目标函数见式(28)、式(29),约束条件为式(13)-式(27)。
| $\begin{gathered} \min f_{3}=\sum\limits_{u=1}^{N_{\text {inc }}^{\prime}} I_{u, t}\left(P_{u, t}^{\prime}-P_{u, t}\right) C_{u, \text { inc }}+ \\ \sum\limits_{v=1}^{N_{\text {dec }}^{\prime}} I_{v, t}\left(P_{v, t}-P_{v, t}^{\prime}\right) C_{v, \text { dec }} \end{gathered} $ | (28) |
| $ \min f_{4}=\sum\limits_{j=1}^{J} 3600 \eta d_{j, t}+\sum\limits_{k=1}^{K} \gamma\left(P_{k, \max }-P_{k, t}\right) $ | (29) |
式中:N′inc,N′dec分别为日内调度上调机组数量和下调机组数量;P′u, t,P′v, t分别为日内调度t时刻上调机组u和下调机组v的实际出力;Pu, t,Pv, t分别为日前计划中t时刻上调机组u和下调机组v的出力;Iu, t,Iv, t分别为机组向上调节和向下调节的状态变量,均为0-1变量。目标函数f3表示在t时刻,各机组在日前调度所得的计划出力的基础上对各机组出力进行调整所花费的上调、下调费用;f4表示在t时刻各机组弃水弃风成本综合;约束条件主要为系统内功率平衡与各设备的物理约束。
4 偏差电量月内滚动法日调度模型求解步骤在各机组月度合约电量和月负荷、水、风预测数据基础上,按上述偏差电量月内滚动调度方法,计算步骤如下。
步骤1:按以式(1)为目标函数,式(5)-式(7)为约束条件的月度电量分解模型将各火电机组合约电量分解,得到各机组初始日计划电量。
步骤2:根据日前预测数据,日内实际负荷、水、风情况和日计划电量,按日前调度模型进行日前调度,日前调度模型目标函数为式(8)-式(12),约束条件为式(13)-式(27)。日前调度得到次日各机组各时刻计划出力。
步骤3:日内调度时,在每一时刻,将日内预测数据和日前调度所得该时刻计划出力代入目标函数式(28)、式(29),在满足日内调度约束条件下求解该时刻最优出力。
步骤4:日调度结束后,将各机组日实际发电量与日前各机组日计划发电量的偏差电量平均分摊到本月剩余各日,更新修正日计划电量。
步骤5:更新次日的水电初始库容、火电初始功率和火电机组的初始启停状态,分别等于该日末时水库容量、火电功率和火电机组启停状态。
步骤6:重复步骤2-步骤5直至月末,月度调度结束。
此外,前文所述日前、日内调度模型为多目标规划模型,为消除量纲的影响,采用式(30)对目标进行归一化,再利用权重系数法[27]进行求解。
| $ f_{i}^{\prime}(x)=\frac{f_{i}(x)-f_{i, \min }\left(x^{\prime}\right)}{f_{i, \max }\left(x^{\prime \prime}\right)-f_{i, \min }\left(x^{\prime}\right)} \quad i=1, 2 $ | (30) |
式中:f′i(x)为归一化后的目标函数;fi(x)为原目标函数;x″,x′分别为f1,f2单目标求解时得到的使目标fi为最大值fi, max(x″)和最小值fi, min(x′)的最优解。
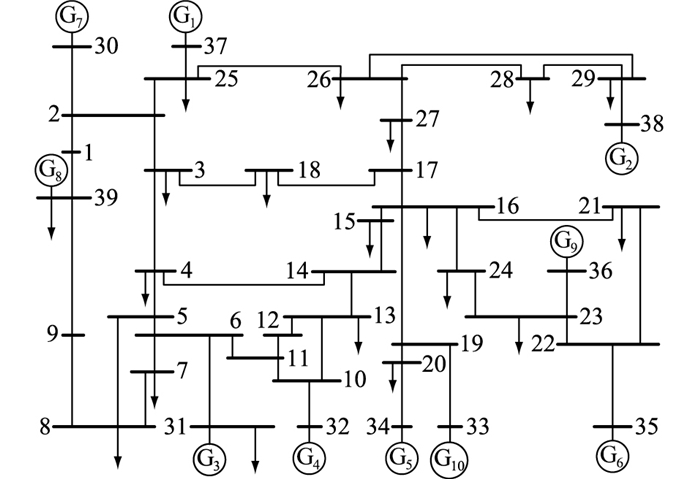
5 算例分析 5.1 原始数据IEEE 39节点系统[28]算例如图 2所示,在此系统中进行为期一个月的调度仿真。图 2中设置机组G1-G6为火电机组,机组G7、G8为风电机组,机组G9、G10为水电机组。各火电机组和水电机组的参数如表 1、表 2所示,其中V0为水库的初始库容。
|
图 2 IEEE 39节点算例 Fig. 2 IEEE 39-bus power grid |
|
|
表 1 火电机组参数 Table 1 Parameters of thermal power units |
|
|
表 2 水电机组参数 Table 2 Parameters of hydropower units |
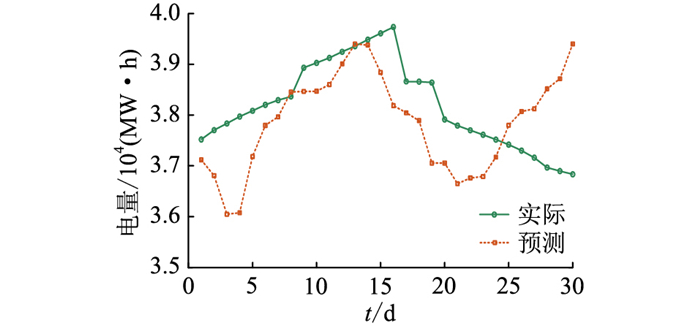
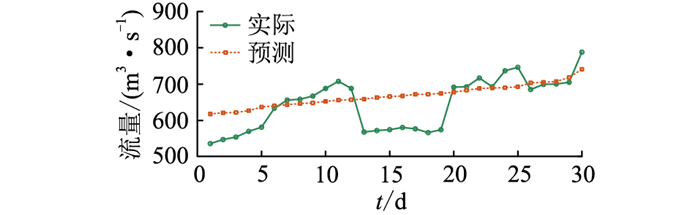
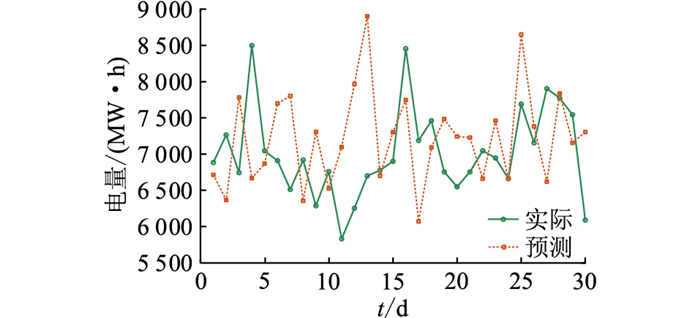
按文中所提方法,首先根据月前预测数据进行火电电量分解,之后要进行连续30 d的调度,当调度日还未来临时其日前负荷预测、当天实际负荷、水、风情况皆为未知。文中采用蒙特卡洛法[29]随机模拟生成调度日日前、日内预测和实际负荷、来水流量、风电出力数据,再利用文中所提日调度模型求解。模拟得实际负荷、水流量、风电预测情况如图 3-图 5所示,可见除风电波动性大导致预测误差较大外,负荷和来水情况最大预测误差分别在4.9%和16.2%左右。该月实际来水比预测少243.3万m3,风电出力比预测多1 387.8 MW ·h,实际需求电量比预测需求多9 848.3 MW ·h。
|
图 3 负荷电量 Fig. 3 Load demand |
|
图 4 来水情况 Fig. 4 Water inflow |
|
图 5 风电出力 Fig. 5 Wind power output |
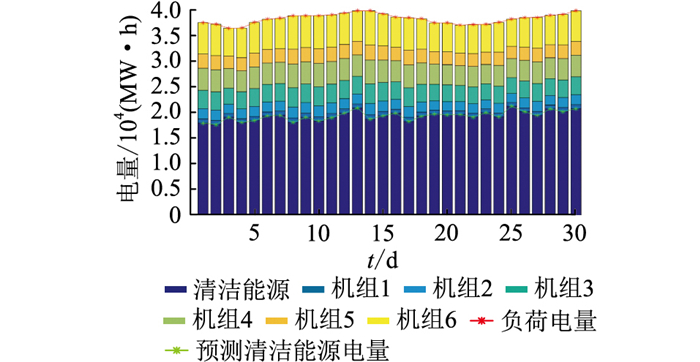
通过前文所提合约分解模型将各机组月度电量分解到日,得到初始日计划电量如图 6所示。假定不考虑机组检修,各火电机组每日合约完成进度方差不超过2.07×10-7。
|
图 6 合约分解结果 Fig. 6 Power decomposition results |
文中日前调度和日内调度皆为双目标优化,将目标函数归一化后采用权重系数法求解。日前和日内2个调度模型的目标皆为1个偏差平衡成本目标和1个节能降耗目标,在同一次仿真中令其权重系数比例相等,在不同权重比例之下的仿真结果如表 3、表 4所示。
|
|
表 3 不同权重仿真结果 Table 3 Simulation results under different weights |
|
|
表 4 不同权重月末机组偏差电量 Table 4 Power deviation under different weights at the end of the month |
如表 3、表 4所示,随着偏差平衡成本目标权重的增加,其偏差平衡成本减小,煤耗增加,弃水和弃风不变。由于水电和风电发电成本很低,优先发电可以减少火电机组煤耗耗。水电机组中G9、G10都有一定的可调节库容,G10可调节库容相对其发电能力较小,调节能力优先,在水流量较大的时刻不可避免地造成了弃水。风电机组的出力波动性较强,且具有反调峰特性,在负荷曲线低估时期不可避免地出现了弃风。文中所提调度方法遵循清洁能源优先发电原则,无论目标权重如何,都能保证清洁能源弃用最小。
由于水电、风电优先出力,两目标权重的变化主要影响火电机组。当增加节能降耗权重时,模型会倾向于减少高煤耗特性机组出力,增加低煤耗特性机组出力,降低系统总发电成本,但会导致月度偏差电量增多,部分机组无法完成合约,公平性降低。
由于机组上下调价格主要受发电成本影响,实际预挂牌交易中能够获得上调摘牌的机组往往发电成本较低,获得下调摘牌的机组往往发电成本较高[3],两目标在一定程度上具有一致性,选择偏差平衡成本占更大权重的方案并不会使系统总煤耗大幅增加,而且可以使月度偏差电量更少,保障中长期交易结果的有效性,调度公平性更高,所以更适用于当前以中长期交易为主的电力市场。
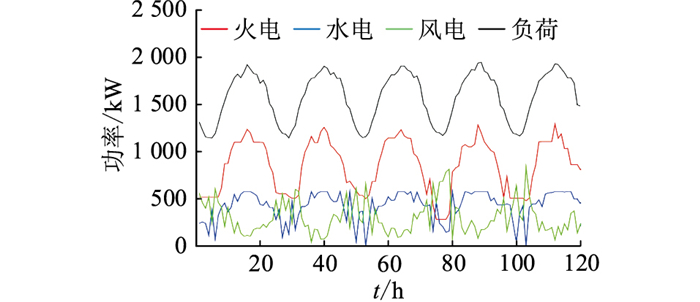
从30 d中选取连续5 d,水、火、风机组出力情况如图 7所示。由图可见火电机组是负荷高峰时期主要承担者,具有调节库容的水电机组凭借其优越的调节能力,主要承担平衡风电出力波动的任务。由此可以看出文中所提调度方法的合理性。
|
图 7 连续5 d机组出力情况 Fig. 7 Generation units output for five consecutive days |
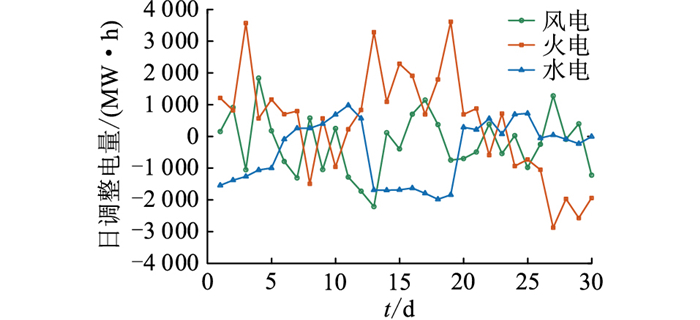
图 8为环境目标和偏差平衡成本目标权重比为0.1 ∶0.9时火电机组日偏差调整电量(日发电量-初始日计划电量),水电、风电机组发电量与预测值的偏差量。由图 8可知,水电、风电机组出力基本遵循“以水定电、以风定电”原则优先发电,算例调度主要通过调整火电出力来适应实际水、风和负荷情况。
|
图 8 各类机组偏差电量 Fig. 8 Power deviation of various power generation units |
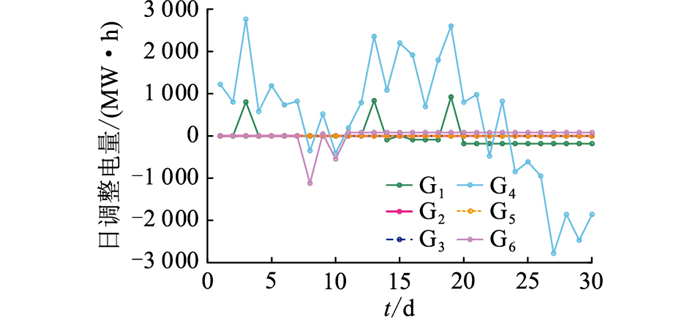
图 9为火电机组日偏差调整电量。0~6 d火电机组上调电量主要由上调价格最低的机组G4和G1承担;7~12 d安排下调价格较低的G6减发电量,机组G4前6日增发了电量,削减了之后每日计划电量,故也减发了部分电量,以抵消之前增发的电量;13~20 d水电来水较少而负荷较高,G4、G1上调发电量,G6增发以抵消之前减发的电量;21~25 d来水情况好转,火电机组G4、G1减发电量,一方面给水电机组提供发电空间,一方面抵消之前增发的电量。总体来看,30 d的调度后,除G4外火电机组月度合约电量完成偏差为0,G4由于上调价格最低而增发一部分电量,保证电力电量平衡。
|
图 9 火电机组调整电量 Fig. 9 Power adjusted by the thermal power units |
综上所述,偏差电量月内滚动调度法利用“价低优先”原则,保证清洁能源优先发电,再通过火电机组日偏差电量月内滚动,使偏差电量在月内自行抵消,达到最小化火电月度偏差电量的目的,最终实现系统月度调度结果最优。
6 结论文中提出适用于预挂牌月偏差平衡机制下水火风电系统的偏差电量月内滚动调度方法。提出中长期月度合约电量分解模型、日前调度模型和日内调度模型,通过算例仿真验证该方法的有效性,并得出以下结论:
(1) 月度合约电量分解到日,作为机组初始日计划电量,以机组日偏差平衡成本最小为目标进行调度,并将日偏差电量在月内滚动的方法可以实现预挂牌平衡机制下月度偏差平衡成本最小。
(2) 文中所提偏差电量月内滚动调度法通过日偏差电量的滚动使得机组偏差电量在月内自行抵消,灵活性较高,可适用于清洁能源、负荷等预测偏差较大的情况。
(3) 文中所提调度方法适用于采用预挂牌月偏差平衡机制的中长期电力市场,该方法须通过合理的价格机制引导,确保调度结果的合理性。
本文得到国网湖南省电力有限公司科技项目“湖南电网新能源消纳能力提升及支撑政策建议研究”(5216A2200004),湖南省科技创新平台与人才计划项目(2019TP1053)资助,谨此致谢!
| [1] |
国家发展改革委, 国家能源局. 电力中长期交易基本规则(暂行)[Z]. 2016. National Development and Reform Commission, National Energy Administration. Basic rules for medium and long-term electricity trading (provisional)[Z]. 2016. (  0) 0) |
| [2] |
贾晨, 杜欣慧. 中长期交易机制下售电公司购电策略优化[J]. 中国电力, 2019, 52(9): 140-147. JIA Chen, DU Xinhui. Optimization of electricity purchasing strategy for electricity retailers under the medium and long-term trading mechanism[J]. Electric Power, 2019, 52(9): 140-147. (  0) 0) |
| [3] |
刘德旭, 王靖, 马光文, 等. 电力市场中的市场力评估研究现状及趋势[J]. 电力需求侧管理, 2021, 23(6): 47-51. LIU Dexu, WANG Jing, MA Guangwen, et al. Development status and trends of market power evaluation in electricity market[J]. Power Demand Side Management, 2021, 23(6): 47-51. DOI:10.3969/j.issn.1009-1831.2021.06.010 (  0) 0) |
| [4] |
肖谦, 喻芸, 荆朝霞. 电力市场的目标、结构及中国电力市场建设的关键问题讨论[J]. 全球能源互联网, 2020, 3(5): 508-517. XIAO Qian, YU Yun, JING Zhaoxia. Discussion on the target and structure of electricity market and the key problems in the construction of China's electricity market[J]. Journal of Global Energy Interconnection, 2020, 3(5): 508-517. (  0) 0) |
| [5] |
姚星安, 曾智健, 杨威, 等. 广东电力市场结算机制设计与实践[J]. 电力系统保护与控制, 2020, 48(2): 76-85. YAO Xing'an, ZENG Zhijian, YANG Wei, et al. Electricity market settlement mechanism design and practice in Guangdong[J]. Power System Protection and Control, 2020, 48(2): 76-85. (  0) 0) |
| [6] |
向恩民, 潘虹锦, 钟磊, 等. 考虑内部多地区间交互协作的复杂省级电力市场交易优化决策[J]. 智慧电力, 2021, 49(3): 59-66. XIANG Enmin, PAN Hongjin, ZHONG Lei, et al. Transaction optimization decision in complex provincial electricity market considering inter regional cooperation[J]. Smart Power, 2021, 49(3): 59-66. DOI:10.3969/j.issn.1673-7598.2021.03.010 (  0) 0) |
| [7] |
湖南省发展和改革委员会. 湖南省电力中长期交易规则(试行)[Z]. 2017. Hunan Provincial Development and Reform Commission. Hunan province electric power medium and long-term trading rules (Trial)[Z]. 2017. (  0) 0) |
| [8] |
谷峰. 电力市场顶层设计与交易现实的博弈妥协: 解读电力中长期交易基本规则[J]. 中国电力企业管理, 2017(1): 32-35. GU Feng. The game compromise between the top-level design of the electricity market and the reality of trading: interpretation of the basic rules of medium and long-term electricity trading[J]. China Power Enterprise Management, 2017(1): 32-35. DOI:10.3969/j.issn.1007-3361.2017.01.008 (  0) 0) |
| [9] |
白杨, 钟海旺, 夏清, 等. 电量协调与成本控制的日内滚动发电计划[J]. 电网技术, 2013, 37(10): 2965-2972. BAI Yang, ZHONG Haiwang, XIA Qing, et al. An intraday rolling scheduling with unit energy coordination and operating cost control[J]. Power System Technology, 2013, 37(10): 2965-2972. (  0) 0) |
| [10] |
汪洋, 苏峰, 邓立, 等. 考虑机组合同电量完成动态均衡的日内安全经济调度[J]. 中国电力, 2016, 49(9): 125-129, 136. WANG Yang, SU Feng, DENG Li, et al. Dynamic intraday rolling scheduling considering electricity quantity progress[J]. Electric Power, 2016, 49(9): 125-129, 136. (  0) 0) |
| [11] |
张晓花, 朱陈松, 路睿, 等. 基于多智能体系统并考虑需求响应的电力系统节能减排调度[J]. 电力需求侧管理, 2019, 21(5): 35-40. ZHANG Xiaohua, ZHU Chensong, LU Rui, et al. Cost-emission dispatch based on multi-agent system considering demand response[J]. Power Demand Side Management, 2019, 21(5): 35-40. DOI:10.3969/j.issn.1009-1831.2019.05.008 (  0) 0) |
| [12] |
高晓松, 李更丰, 肖遥, 等. 基于分布鲁棒优化的电-气-热综合能源系统日前经济调度[J]. 电网技术, 2020, 44(6): 2245-2254. GAO Xiaosong, LI Gengfeng, XIAO Yao, et al. Day-ahead economical dispatch of electricity-gas-heat integrated energy system based on distributionally robust optimization[J]. Power System Technology, 2020, 44(6): 2245-2254. (  0) 0) |
| [13] |
田书, 赵哲林, 杜少通. 基于改进多目标差分进化算法的节能优化调度[J]. 武汉大学学报(工学版), 2019, 52(12): 1091-1096, 1105. TIAN Shu, ZHAO Zhelin, DU Shaotong. Energy-saving optimal scheduling based on improved multi-objective differential evolution algorithm[J]. Engineering Journal of Wuhan University, 2019, 52(12): 1091-1096, 1105. (  0) 0) |
| [14] |
胡静哲, 王旭, 蒋传文, 等. 计及综合能源服务商参与的电力系统低碳经济调度[J]. 电网技术, 2020, 44(2): 514-522. HU Jingzhe, WANG Xu, JIANG Chuanwen, et al. Low-carbon economic dispatch of power system considering participation of integrated energy service providers[J]. Power System Technology, 2020, 44(2): 514-522. (  0) 0) |
| [15] |
彭春华, 刘兵, 孙惠娟. 基于分类不确定性集合的电力系统环境经济鲁棒调度[J]. 中国电机工程学报, 2020, 40(7): 2202-2212, 2399. PENG Chunhua, LIU Bing, SUN Huijuan. Environmental/economic/robust dispatch of power system based on classification uncertainty sets[J]. Proceedings of the CSEE, 2020, 40(7): 2202-2212, 2399. (  0) 0) |
| [16] |
姚方, 王佳伟, 文福拴, 等. 计及碳税的含风电和储能的电力系统经济调度[J]. 电力科学与技术学报, 2019, 34(1): 37-46. YAO Fang, WANG Jiawei, WEN Fushuan, et al. Economic dispatch for a power system containing wind power and energy storage with carbon tax considered[J]. Journal of Electric Power Science and Technology, 2019, 34(1): 37-46. (  0) 0) |
| [17] |
GHORBANI N. Combined heat and power economic dispatch using exchange market algorithm[J]. International Journal of Electrical Power & Energy Systems, 2016, 82: 58-66. (  0) 0) |
| [18] |
YANG J, ZHANG G S, MA K. Hierarchical dispatch using two-stage optimisation for electricity markets in smart grid[J]. International Journal of Systems Science, 2016, 47(15): 3529-3536. DOI:10.1080/00207721.2015.1090042 (  0) 0) |
| [19] |
HU F T, HUGHES K J, INGHAM D B, et al. Dynamic economic and emission dispatch model considering wind power under energy market reform: a case study[J]. International Journal of Electrical Power & Energy Systems, 2019, 110: 184-196. (  0) 0) |
| [20] |
谢蒙飞, 贾泽斌, 张帆, 等. 计及电量分解的高比例水电电网短期调度方法[J]. 水力发电学报, 2021, 40(1): 54-64. XIE Mengfei, JIA Zebin, ZHANG Fan, et al. Method of short-term scheduling for high-proportion hydropower grid considering energy decomposition[J]. Journal of Hydroelectric Engineering, 2021, 40(1): 54-64. (  0) 0) |
| [21] |
孙悦, 王啸宇, 刘迎迎, 等. 适应大规模风电并网的超短期调度策略研究[J]. 电力电容器与无功补偿, 2018, 39(6): 179-185. SUN Yue, WANG Xiaoyu, LIU Yingying, et al. Study on ultra-short term dispatching strategies for large-scale wind power integration[J]. Power Capacitors & Reactive Power Compensation, 2018, 39(6): 179-185. (  0) 0) |
| [22] |
李利利, 管益斌, 耿建, 等. 月度安全约束机组组合建模及求解[J]. 电力系统自动化, 2011, 35(12): 27-31, 64. LI Lili, GUAN Yibin, GENG Jian, et al. Modeling and solving for monthly security constrained unit commitment problem[J]. Automation of Electric Power Systems, 2011, 35(12): 27-31, 64. (  0) 0) |
| [23] |
赵书强, 陈佳君, 李志伟, 等. 含可再生能源的电力系统周优化运行策略[J]. 中国电力, 2020, 53(3): 8-17, 51. ZHAO Shuqiang, CHEN Jiajun, LI Zhiwei, et al. An optimal weekly operation strategy for power systems with renewable energy[J]. Electric Power, 2020, 53(3): 8-17, 51. (  0) 0) |
| [24] |
苗树敏, 罗彬, 申建建, 等. 考虑市场过渡和中长期合约电量分解的水火电短期多目标发电调度[J]. 电网技术, 2018, 42(7): 2221-2231. MIAO Shumin, LUO Bin, SHEN Jianjian, et al. Short-term multi-objective hydro-thermal generation dispatch considering electricity market transition and mid-and long-term contract decomposition[J]. Power System Technology, 2018, 42(7): 2221-2231. (  0) 0) |
| [25] |
许传龙, 张粒子, 陈大宇, 等. 基于预招标的月度偏差电量平衡机制及其多周期发电调度优化模型[J]. 中国电机工程学报, 2019, 39(17): 5085-5094, 5289. XU Chuanlong, ZHANG Lizi, CHEN Dayu, et al. A monthly balancing mechanism based on pre-bidding and its multi-period generation schedule optimization model[J]. Proceedings of the CSEE, 2019, 39(17): 5085-5094, 5289. (  0) 0) |
| [26] |
路轶, 胡晓静, 孙毅, 等. 适应高水电占比的电力现货市场机制设计与实践[J]. 电力系统自动化, 2021, 45(9): 162-170. LU Yi, HU Xiaojing, SUN Yi, et al. Design and practice of electricity spot market mechanism adapting to characteristics of high proportional hydropower[J]. Automation of Electric Power Systems, 2021, 45(9): 162-170. (  0) 0) |
| [27] |
刘辉, 江千军, 桂前进, 等. 考虑供需综合因素的电网检修计划最优决策模型[J]. 中国电力, 2021, 54(6): 159-167. LIU Hui, JIANG Qianjun, GUI Qianjin, et al. Optimal decision-making model for power grid maintenance scheduling considering comprehensive supply-demand factors[J]. Electric Power, 2021, 54(6): 159-167. (  0) 0) |
| [28] |
孙淑琴, 颜文丽, 吴晨悦, 等. 基于原-对偶内点法的输电断面有功安全校正控制方法[J]. 电力系统保护与控制, 2021, 49(7): 75-85. SUN Shuqin, YAN Wenli, WU Chenyue, et al. Transmission sections; AP clustering algorithm; line outage distribution factor; safety correction of active power flow[J]. Power System Protection and Control, 2021, 49(7): 75-85. (  0) 0) |
| [29] |
杨萌, 艾欣, 唐亮, 等. 计及风险规避的售电公司平衡市场优化交易策略研究[J]. 电网技术, 2016, 40(11): 3300-3309. YANG Meng, AI Xin, TANG Liang, et al. Optimal trading strategy in balancing market for electricity retailer considering risk aversion[J]. Power System Technology, 2016, 40(11): 3300-3309. (  0) 0) |
2. Hunan Key Laboratory of Energy Internet Supply-demand and Operation, Changsha 410004, China;
3. School of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410114, China

 禹海峰(1987), 男, 硕士, 高级工程师, 从事主电网规划、能源电力供应保障、新能源消纳相关工作(E-mail:
禹海峰(1987), 男, 硕士, 高级工程师, 从事主电网规划、能源电力供应保障、新能源消纳相关工作(E-mail: