文章编号: 2096-3203(2021)06-0025-09 中图分类号: TM715
2. 国网江西省电力有限公司, 江西 南昌 330096
随着能源革命的推进及双碳目标[1]的落实,传统各能源系统单独规划、运行的模式由于存在能源利用效率低、灵活性差等缺点,已然不能满足绿色用能、低碳环保的需要。在此背景下,强调多能互补及清洁高效的综合能源系统(integrated energy system,IES)也应运而生,随着研究的深入,IES被广泛用作乡镇、园区、楼宇的供能系统。由于IES中各能流相互影响,具有较强的耦合关系[2],因此对IES进行高效规划和控制需要对多种能源需求情况有全面的了解,这对IES的负荷预测提出了巨大挑战。
传统电力系统中,用户用电负荷具有随机性[3-6]。目前,电力系统负荷预测已经有了较为成熟的体系。电力负荷预测模型可以大致分为:时间序列模型、多元回归模型[7]、机器学习模型[8]及神经网络模型[9]。近年来,深度学习算法凭借其突出的自动特征提取能力及非线性拟合能力受到了广大学者的青睐。为了挖掘时间序列的关联性,文献[10]利用相空间重构对负荷数据进行了高维相空间投影,使历史数据按关联性重新排列,并采用深度信念网络进行建模与预测。该方法虽然能够利用时间序列的特性,但缺乏灵活性,无法依据数据的改变自动筛选出重要特征信息。卷积神经网络(convolutional neural networks,CNN)凭借其高度的特征总结能力及深度的非线性结构,能够有效减少人工提取特征带来的误差[11]。文献[12]利用CNN对日期信息、历史数据、天气数据等进行自动特征筛选,并将结果输入长短期记忆(long short-term memory,LSTM)网络。文献[13]以文献[12]为基础,简化了网络模型,并加入Attention机制,能有效减少历史信息丢失并加强重要信息的影响,预测精度显著提高。
相较于传统电力负荷预测,涉及IES的多能负荷预测中,通常需要分别分析冷、热、电负荷的用能特性,建立3种不同的预测模型,耗费大量计算资源和时间成本。目前针对IES的负荷预测研究仍然较少[14],基于对传统电力系统负荷预测的研究,文献[15]采用Copula理论对特征相关性进行分析,并利用核主成分分析筛选特征后输入广义回归神经网络进行预测。文献[16]采用灰色关联度分析证明了冷、热、电负荷具有很高的相关性,进而提出改进LSTM模型,分别对冷、热、电负荷进行预测。上述方法取得了良好的预测效果,但忽略了多能负荷间多时间尺度的复杂耦合关系,仅将多能负荷历史数据简单串联作为模型输入。为此文献[17]采用迁移学习中的多任务学习(multi-task learning,MTL)原理,对多能负荷进行统一建模,从而挖掘多能负荷的耦合性,提升最终的预测结果,同时证明了MTL原理的有效性。文献[18]提出LSTM-MTL预测模型,引入一个参数共享层并辅以沙普利加和解释技术对模型进行可视化分析,取得了较好的预测精度。
然而上述IES多能预测的文献中,并未对历史序列大数据进行有效挖掘,且MTL模型通常只是添加了一层参数共享层,无法有效降低模型复杂程度。因此文中以现有研究为基础提出一种基于迁移学习的改进领域自适应神经网络(domain adaptive neural network,DaNN)模型对冷、热、电负荷进行统一建模与预测,旨在降低模型规模并通过多个参数共享卷积层挖掘各能源预测领域间的关联性,最终提升IES的负荷预测精度。
1 基本原理 1.1 CNNCNN是一种包含卷积计算且具有深度结构的前馈神经网络。目前,CNN主要应用于计算机视觉(computer vision,CV)领域,凭借其优秀的特征提取能力在近些年受到了学者的广泛关注,并涌现出如AlexNet[19]、VGGNet等高性能的深度CNN模型构筑。
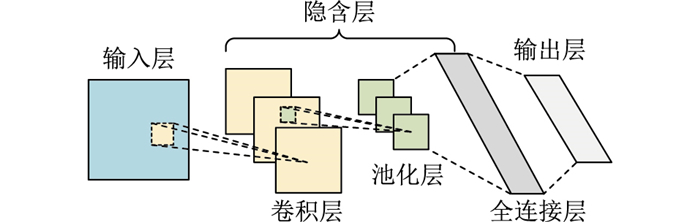
常见的CNN由输入层、隐含层和输出层构成,不同于传统神经网络(neural networks,NN),CNN的隐含层分为卷积层、池化层和全连接层。CNN通过卷积和池化层的计算可将数据重构,从而整合有效信息并提高特征提取效率[13]。常见的CNN结构如图 1所示。
|
图 1 CNN结构 Fig. 1 Structure of CNN |
随着人工智能和机器学习领域的飞速发展,NN、决策树和支持向量机等智能模型在各学科的研究中都受到了极大重视,然而传统的学习模型通常是针对特定问题建立的,不具备可迁移性,在面临新问题时研究者不得不从零开始建立新的模型。针对一些相似性较高的问题,有学者提出了迁移学习的概念,迁移学习顾名思义就是“举一反三”,通过原问题和新问题之间的相似性将基于原问题建立的模型应用于新问题中。其中以深度迁移学习最为高效,通过微调已有的深度网络可以节省模型的训练时间,提高学习精度[20]。
为了解决迁移学习中源域和目标域数据的适配问题,Muhammad Ghifary等人提出了DaNN[21]。DaNN仅由特征层和分类器层组成,通过最大均值差异(maximum mean discrepancy,MMD)计算源域和目标域的分布差异并将其计入损失函数中。设存在满足p分布的随机变量x= {x1, x2, …, xn} ~p,与满足q分布的随机变量y= {y1, y2, …, ym} ~q。MMD度量的计算表达式为:
| $ \mathit{\boldsymbol{\lambda }}_{{\rm{MMD}}}^2(\mathit{x}, \mathit{y}) = \parallel \frac{1}{n}\sum\limits_{i = 1}^n {\varphi ({\mathit{x}_i}) - \frac{1}{m}\sum\limits_{j = 1}^m \varphi ({\mathit{y}_i})} \parallel _H^2 $ | (1) |
式中:φ(·)为映射函数,通过将原数据映射至再生核希尔伯特空间(reproducing kernel Hilbert space,RKHS),并计算x与y在RKHS中均值的距离(采用
| $ \begin{array}{l} \;\;\;\;\;\;\;{\bf{ \pmb{\mathsf{ λ}} }}_{{\rm{MMD}}}^2(x,y) = \parallel \frac{1}{{{n^2}}}\sum\limits_{i = 1}^n {\sum\limits_{i' = 1}^n {K({x_i},{x_{i'}})} } - \\ \frac{2}{{nm}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {K({x_i},{y_j})} } + \frac{1}{{{m^2}}}\sum\limits_{j = 1}^m {\sum\limits_{j' = 1}^m {K({y_j},{y_{j'}})} } {\parallel _H} \end{array} $ | (2) |
式中:K(·)为核函数,通常采用高斯核函数。迁移学习中,通过减小MMD的数值,能够使目标域和源域的数据分布尽可能接近,从而实现源域知识向目标域的迁移,因此DaNN的损失函数为:
| $ {L_{{\rm{DaNN}}}} = {L_{{\rm{NN}}}} + \gamma \mathit{\boldsymbol{\lambda }}_{{\rm{MMD}}}^2({\mathit{q}_{\rm{s}}}, {\mathit{q}_{\rm{t}}}) $ | (3) |
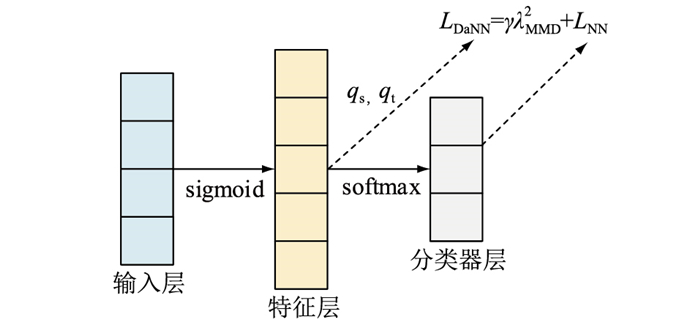
式中:LDaNN为DaNN的损失函数;LNN为NN的损失函数;γ为MMD的权重因子,文中取0.25;qs,qt分别为源域和目标域数据在特征层上的输出。DaNN的结构如图 2所示。
|
图 2 DaNN结构 Fig. 2 Structure of DaNN |
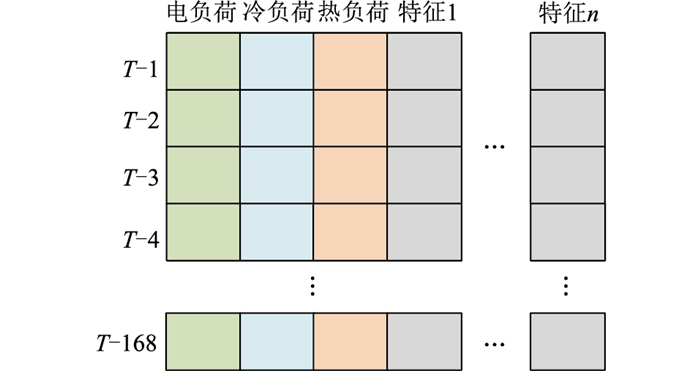
随着智能测量仪表的普及和通信传输设备的发展,预测问题中能够获得的历史数据量空前提升,因而合理利用海量历史数据也成为模型性能提升的关键。在传统的时间序列和机器学习预测模型中,过多的特征输入会导致模型的维度灾难。研究者通常采用过去一小时或一天相同时刻的历史数据作为短期预测的特征输入模型,然而此方法忽略了一些潜在相关的历史数据,造成有效信息的浪费。同时,IES的出现使得历史数据成倍增长,为了尽可能掌握IES中多能负荷变化的规律并有效减少模型维数,文中采用CNN模型提取历史数据特征,并构建多能负荷特征图作为CNN模型的输入。多能负荷特征图通过将不同类别时间序列数据横向展开并按时间纵向堆叠形成。以含冷、热、电负荷的IES为例,其中待预测时刻T的电负荷特征如图 3所示。
|
图 3 电负荷特征 Fig. 3 Feature picture of electrical load |
图 3中各列为不同种特征的时间序列,各行为不同时刻(以小时为单位)的特征数值。由于IES中各能源的用能特性有较强耦合关系,因此电负荷的特征图中包含了冷负荷和热负荷的用能时间序列。特征1~特征n可分别代表小时、日类型等日期序列或温度、湿度、辐照等天气序列。为了控制特征图的大小、提高计算效率,文中以一周为上限,即取待预测时刻T前一周的历史数据构成负荷特征图。冷负荷与热负荷的特征图可以由相同方法构成,仅需分别调换前3列的位置,即当构建冷负荷特征图时采用冷、电、热的顺序,而构建热负荷特征图时采用热、冷、电的顺序。
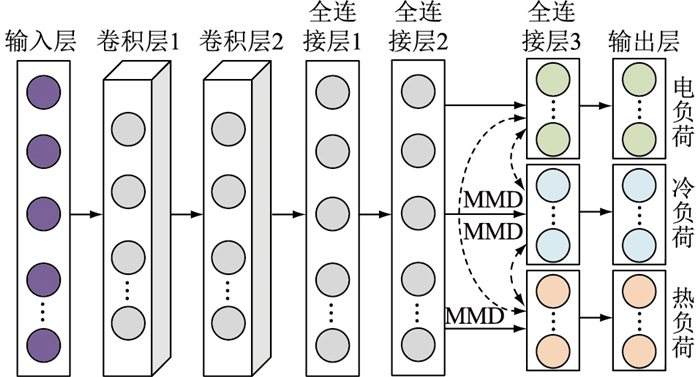
2.2 多能负荷预测模型结构与流程为减少IES中构建多能预测模型的成本,提高运算效率并充分利用数据间耦合关系,文中采用基于迁移学习的DaNN对冷、热、电负荷进行统一建模与预测。由于传统DaNN模型仅由2层神经元构成,无法很好地对序列特征进行挖掘,因此在传统DaNN的基础上加入CNN结构,利用CNN对复杂特征进行压缩和降维,改进后的DaNN结构如图 4所示。改进DaNN由输入层、卷积层、全连接层和输出层构成,并在全连接层2、3之间加入MMD自适应度量计算源域和目标域的差异。其中,输入层分别读入待预测时刻的冷、热、电负荷特征图,卷积层包含了1.1节中提到的卷积和池化计算,全连接层与一般NN隐含层结构相同,输出层依据模型输入的不同分别输出待预测时刻的用能负荷预测值,通过最小化网络损失函数,即可最大限度缩小电负荷与冷、热负荷特征的分布差异从而使模型对冷、热负荷预测达到触类旁通的效果。图 4中,卷积层1、2与全连接层1、2为参数共享层,全连接层3依据任务的不同划分为3个神经元数相同的独立全连接层,图中分别采用绿色、蓝色和橙色的神经元代表电、冷、热负荷各自独立的全连接层。
|
图 4 改进DaNN结构 Fig. 4 Structure of improved DaNN |
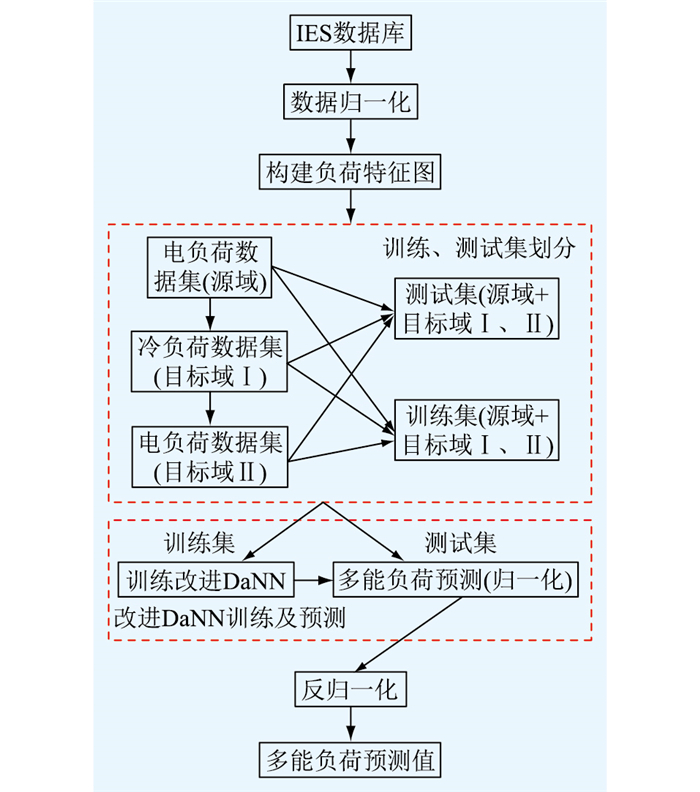
基于IES数据库内的冷、热、电负荷及对应的天气、日期等原始数据,所提改进DaNN模型的预测流程如图 5所示,具体流程如下。
|
图 5 改进DaNN模型预测流程 Fig. 5 Flow chart of improved DaNN forecasting model |
步骤1:对原始数据分别进行极差归一化并保存各自最大、最小值,以便进行反归一化。
步骤2:分别构建电、冷、热负荷特征图并划分目标域及源域数据集。其中,源域数据集包含传统电负荷数据,目标域数据集共有2个,目标域Ⅰ为冷负荷数据,目标域Ⅱ为热负荷数据。最后在源域与目标域数据集上分别按7 ∶3划分训练集与测试集。
步骤3:基于CNN及DaNN的原理构建改进DaNN模型,并将步骤2中源域和目标域的训练集代入训练。文中采用交叉验证的方法优化部分网络超参数。
步骤4:利用步骤3中训练好的改进DaNN预测模型在测试集上分别对冷、热、电负荷进行预测,得到多能负荷的归一化预测值。
步骤5:基于步骤1中保存的最值,对步骤4中取得的归一化预测值进行反归一化,即可得到IES中冷、热、电负荷的预测值。
2.3 模型损失函数通常迁移学习模型仅由单个源域向单个目标域迁移,例如DaNN模型通过最小化式(3)使得源域与目标域的特征分布尽可能接近,并利用具有参数共享机制的分类器层对目标域特征进行处理,从而达到一隅三反的效果。然而IES中存在多种能源形式,为减少模型的构筑成本并充分利用传统电负荷预测知识,文中将冷、热负荷分别划分为目标域Ⅰ与目标域Ⅱ。
随着目标域个数的增加,为使改进DaNN模型能够全面衡量源域与各目标域的特征分布情况,损失函数不仅需要考虑源域与不同目标域的MMD值,还需要加入各目标域之间的MMD值,避免参数共享层输出的特征在各目标域中分布差距较大而影响迁移结果。因此,改进DaNN的损失函数可在式(3)的基础上改为:
| $ \begin{array}{l} \;{L_{{\rm{DaNN}}}} = {L_{{\rm{NN}}}} + {\gamma _1}{\bf{ \pmb{\mathsf{ λ}} }}_{{\rm{MMD}}}^2({q_{\rm{s}}},{q_{{\rm{t1}}}}) + \\ {\gamma _2}{\bf{ \pmb{\mathsf{ λ}} }}_{{\rm{MMD}}}^2({q_{\rm{s}}},{q_{{\rm{t2}}}}) + {\gamma _3}{\bf{ \pmb{\mathsf{ λ}} }}_{{\rm{MMD}}}^2({q_{{\rm{t}}1}},{q_{{\rm{t2}}}}) \end{array} $ | (4) |
文中采用均方误差(mean square error,MSE)衡量目标域及源域上所有预测的误差。γ1,γ2,γ3为MMD的权重因子,文中均取1/12;qs,qt1,qt2分别为电、冷、热负荷在全连接层2的输出特征。
以包含电、冷、热3种能源的IES为例,LNN可以表示为:
| $ \begin{array}{l} {L_{{\rm{NN}}}} = {w_1}{f_{{\rm{MSE}}}}({p_s},{\widehat p_{\rm{s}}}) + {w_2}{f_{{\rm{MSE}}}}({p_{t1}},{\widehat p_{{\rm{t1}}}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{w_3}{f_{{\rm{MSE}}}}({p_{t2}},{\widehat p_{{\rm{t2}}}}) \end{array} $ | (5) |
式中:fMSE(·)为均方误差函数;p为负荷的实际值;
文中所提改进DaNN通过最小化式(4)使得冷、热、电负荷在全连接层2上输出的特征分布尽可能相同,最终依据任务的不同将特征输入对应的全连接层3即可获得归一化的负荷预测值,再经过反归一化可得到待预测负荷的预测值。
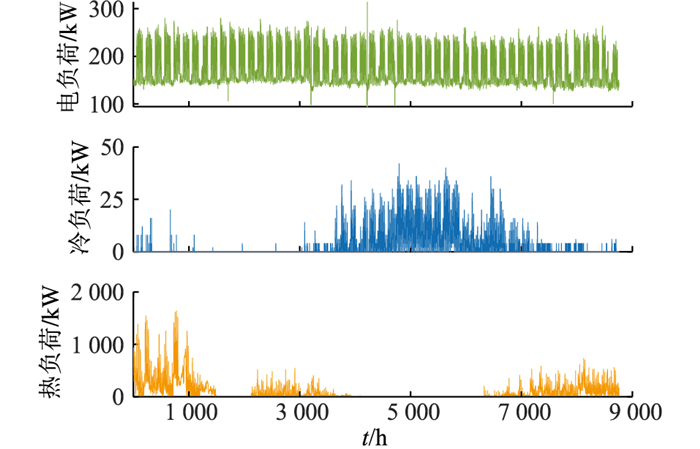
3 IES算例分析 3.1 IES负荷数据采用美国国家可再生能源实验室网站[22]中某楼宇级IES的开源实测值验证所提改进DaNN预测模型的有效性。该楼宇级IES由冷、热、电系统组成,采集数据包括冷、热、电负荷数据及对应的星期、时间、温度、平均全球辐照度和平均全球南纬90°辐照度。各数据的采集时长为1 a,以小时为单位。其中,冷、热、电负荷全年的用能曲线如图 6所示。
|
图 6 IES负荷实测数据 Fig. 6 Measured data of IES load |
上述原始数据已经过清洗和校正,文中将数据集第8~258天作为训练集,第259~365天作为测试集。算例中对所提模型的验证在Matlab环境与Python环境下基于Pytorch库进行。
3.2 预测评价指标文中模型最终能够给出冷、热、电负荷的确定性预测值,对于确定性预测,通常采用平均绝对百分比误差(mean absolute percentage error,MAPE)与均方根误差(root mean square error,RMSE)来衡量预测效果。由于冷、热负荷实际值中存在较多零值,如直接采用MAPE计算会出现无穷值,因此文中追加采用平均绝对误差(mean absolute error,MAE)衡量冷、热负荷的预测精度。
MAPE,MAE,RMSE的表达式定义分别如下:
| $ {K_{{\rm{MAPE}}}} = \frac{1}{k}\sum\limits_{i = 1}^k {|\frac{{{P_i} - {{\widehat p}_i}}}{{{P_i}}}} | \times 100\% $ | (6) |
| $ {K_{{\rm{MAE}}}} = \frac{1}{k}\sum\limits_{i = 1}^k {|{P_i} - {{\widehat p}_i}} | $ | (7) |
| $ {K_{{\rm{RMSE}}}} = \sqrt {\frac{1}{k}\sum\limits_{i = 1}^k {({P_i} - {{\widehat p}_i}} {)^2}} $ | (8) |
式中:k为待预测样本个数;pi为i时刻负荷实际值;
基于2.1节所述,将上文数据集中各特征的时间序列按时间纵向展开、依类别横向排列即可得到电、冷、热负荷的特征图。其中负荷特征图中各特征的排列方式如表 1所示。
|
|
表 1 特征排列方式 Table 1 Feature arrangement |
表 1中一共8列特征,并且电、冷、热负荷的特征图仅前3列的排列有区别,后5列完全相同,这样能够避免MMD度量过大造成损失函数数值骤增而影响网络参数的训练和迁移学习的效果。
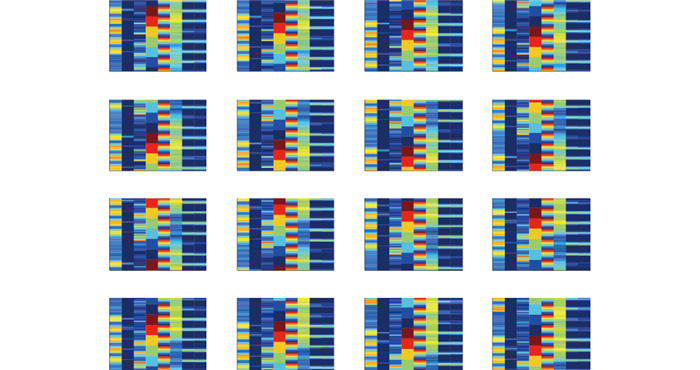
由2.1节可知负荷特征图纵坐标为168,因此采用168×8像素的负荷特征图作为改进DaNN的输入。图 7为训练集上随机选取的16个时刻对应的电负荷特征图。
|
图 7 电负荷特征图 Fig. 7 Picture of electrical load feature |
图 7中颜色越接近暖色代表对应位置的像素点值越大,反之,越接近冷色代表对应位置的值越小。通过负荷特征图的构建和卷积层的采用能够在避免大量增加模型复杂度的前提下尽可能多地利用历史数据信息,提升预测精度。
3.4 改进DaNN模型构建传统CNN卷积层一般采用3×3或者5×5的二维卷积核,且池化层也采用2×2的二维核进行计算。而负荷特征图中各特征之间区别较大,若采用二维卷积核会使不相关的变量融合从而导致严重的信息丢失。因此改进DaNN卷积层1、2的卷积核与池化核都选用一维,通过纵向对各特征时间序列进行卷积和池化操作,提取历史关键信息,并将不同特征间的差异性保留至全连接层。
模型采用Adam优化器优化网络参数,并采用交叉验证法对神经元和卷积核等超参数进行调优。经过优化的网络超参数如表 2所示。由2.2节可知,依据预测目标的不同,全连接层3及输出层由负责电、冷、热负荷预测的3个独立网络构成。因此,表 2中全连接层3和输出层后带有(×3)符号。
|
|
表 2 改进DaNN超参数 Table 2 Super-parameter of improved DaNN |
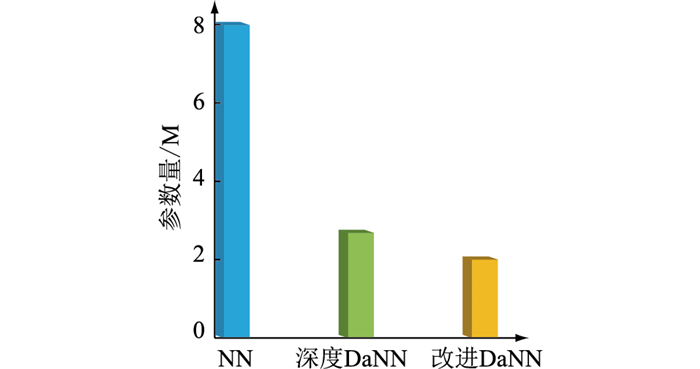
为证明采用CNN处理历史特征并利用DaNN原理进行知识迁移能够有效减小预测模型的参数,文中对改进DaNN、深度DaNN与NN的参数量进行比较。以表 2中改进DaNN模型为例,网络参数量为1.99 M;若保持输入、输出维数相同而将卷积层替换为全连接层(深度DaNN), 则网络参数量为2.68 M;若不采用迁移学习模型而改用3个独立的NN模型则参数量可达8.03 M。上述模型的参数量对比如图 8所示。
|
图 8 模型参数量柱状图 Fig. 8 Histogram of the number of model parameters |
由图 8中不同模型网络参数的对比不难发现,通过引入卷积层及迁移学习模型可将相同输入输出的神经网络规模缩减至之前的1/4,从而大幅降低训练难度并减少计算开支。
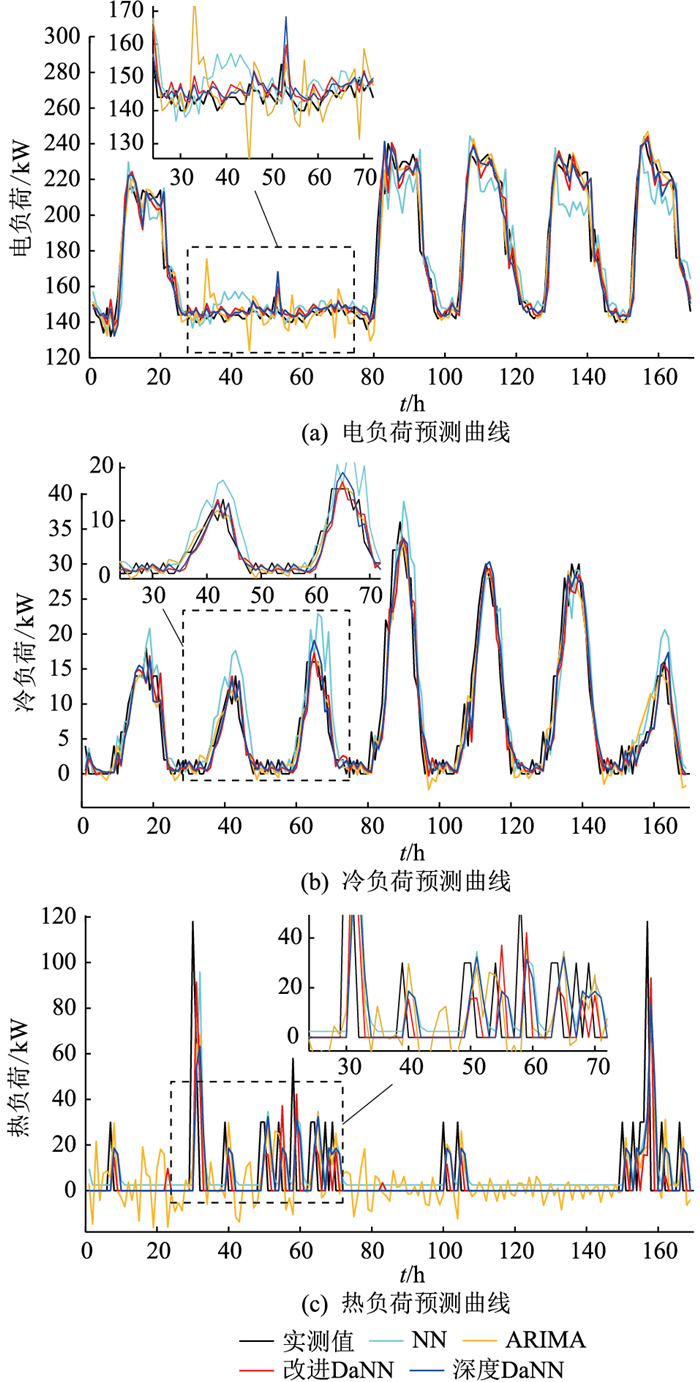
3.5 预测结果为了验证文中所提改进DaNN模型的有效性,分别采用深度DaNN模型、NN模型、差分整合移动平均自回归(autoregressive integrated moving average model,ARIMA)模型对测试集进行预测,预测步长为1 h。其中深度DaNN仅将改进DaNN的卷积层1、2替换为神经元个数为168×8的全连接层,即将负荷特征图平铺为一维特征输入,其余超参数与表 2中相同;NN模型在深度DaNN的基础上,取消了参数共享层,即所有层都带有(×3)符号;ARIMA模型采用赤池信息准则(Akaike information criterion,AIC)[8]确定模型阶数,其中ARIMA电(22,1,18),ARIMA冷(24,1,19),ARIMA热(25,1,20),括号中依次为自回归项数,滑动平均项数和差分次数。测试集上部分待预测日(第265~272天,共7 d)的预测曲线与实测负荷曲线如图 9所示。
|
图 9 多能预测结果 Fig. 9 Forecast results of various type of energy |
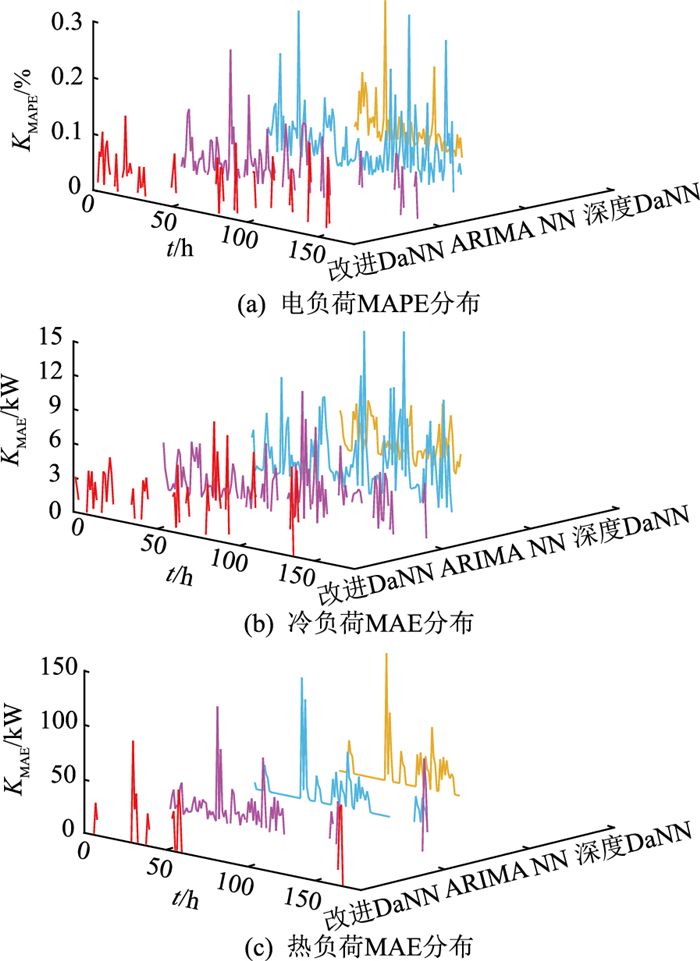
图 9(a)中,第24~72小时为周末,此时电负荷明显下降,然而传统时间序列的ARIMA模型拟合非线性能力不强,容易受到负荷突变的扰动,因此在第24~72小时出现较大波动,无法很好地跟随电负荷的变化,这一情况在图 9(c)的热负荷预测中更为明显。由图 6可知,相较于全年比较平稳的电负荷与用能时段较为集中的冷负荷,热负荷的用能分散性较大,且非线性极强,导致ARIMA时间序列模型的预测值出现较大的波动,完全无法拟合热负荷的用能负荷曲线。为了更加直观地了解几种模型的预测效果,图 10为各模型第265~272天预测结果小时级的误差分布,其中采用MAPE衡量电负荷的误差分布,采用MAE衡量冷、热负荷的误差分布。
由图 10中可见,对于电负荷和冷负荷这类变化较为平稳的负荷,文中所提改进DaNN和ARIMA的误差分布较为均匀,而NN和深度DaNN由于未采用CNN等特征整合提取算法而输入了过多未经筛选的特征,导致模型维度过高,影响了模型最终的训练结果;当出现非线性极强的热负荷时,ARIMA的预测效果明显下降,而改进DaNN、深度DaNN与NN模型凭借其优秀的非线性拟合能力给出了相对较好的结果,但可以明显看出无论是对比热负荷MAE的峰值还是均值,改进DaNN模型都明显小于未采用迁移学习的NN模型和未采用CNN提取特征的深度DaNN模型。通过观察图 6中冷、热负荷曲线和图 9(b)、(c)不难发现,冷、热负荷存在明显耦合,当冷负荷较大时,热负荷基本很小或者为零值,反之亦然。改进DaNN模型也正是利用了多领域数据中的关联性,对冷、热、电负荷进行统一建模,从而有效减少了热负荷的预测误差。这也说明了迁移学习的采用能够有效挖掘不同领域数据的耦合关系并提升最终的预测精度。
|
图 10 多能预测结果误差分布 Fig. 10 Error distribution of multi energy forecast results |
为了更加全面地验证所提改进DaNN的预测效果,文中计算了各模型在全部测试集上的MAPE、MAE和RMSE指标,其中对于电负荷采用MAPE与RMSE指标,而冷、热负荷采用MAE与RMSE指标。各指标的计算结果如表 3所示。
|
|
表 3 各模型预测效果 Table 3 Forecast performance of each model |
表 3中,改进DaNN在电、冷、热负荷预测中均有较小的评价指标,说明改进DaNN在综合能源预测中有较强优越性。相比于基准模型ARIMA、深度DaNN与NN,所提改进DaNN的优势总结如下:
(1) 改进DaNN采用CNN作为特征整合与筛选工具,通过卷积层1、2有效整合了有利信息并大幅降低了模型的复杂程度,模型凭借较少的维度更加易于训练。而深度DaNN和NN由于没有上述特征整合过程,模型的维度大幅增加,不利于模型的训练与收敛,致使其在传统的电负荷预测及冷、热负荷预测领域效果大打折扣。
(2) 改进DaNN采用了迁移学习理论,通过统一建模预测的方式建立多层参数共享层,并有效利用各领域数据的耦合关系,提升了最终的预测精度。而ARIMA和NN模型只是针对不同负荷单独训练及预测,因此会出现ARIMA模型虽然在电、冷负荷的预测中表现较好,却在非线性较强的热负荷预测中表现不佳的现象。同样的,虽然NN模型有较强的非线性拟合能力,但对热负荷的预测精度依然不如改进DaNN。
(3) 除了模型的预测精度外,图 8直观展示了相较于NN模型和深度DaNN模型,改进DaNN模型由于采用了卷积层和参数共享层,能够有效缩减模型规模并节约计算资源;虽然ARIMA自身的算法较为简单,但采用AIC理论优化穷举参数不同的ARIMA模型也会耗费大量计算资源。
4 结论文中针对IES中的冷、热、电多能负荷预测问题,提出了一种基于迁移学习的改进DaNN模型。首先将多能负荷数据按一定方法形成对应的负荷特征图,其次通过改进DaNN模型中的参数共享CNN层和参数共享全连接层对负荷特征图进行特征整合,最后通过3个各自独立的全连接层和输出层分别对冷、热、电负荷进行预测。文中还采用了了美国国家可再生能源实验室的楼宇级IES实测数据对所提模型的有效性进行了验证,并与基准负荷预测模型进行对比,得到以下结论:
(1) 改进DaNN通过引入CNN和参数共享层减少了模型的参数量及维度并节约了计算资源;
(2) 改进DaNN挖掘了不同领域数据的耦合特性,并通过数据之间的关联性提升了预测的精度。
文中模型涉及3个不同领域的预测问题,因此在模型的规划和超参数调优上仅基于交叉验证结果进行了手动粗调,难以寻得最优的超参数;改进DaNN仅在全连接层3前考虑了MMD指标,当冷、热负荷波动较大时,各特征可能在卷积层就出现了明显的分化,从而使MMD过大而影响训练,因此还可以在更多位置加入MMD计算,保证特征分布的相似性;所提改进DaNN模型是以冷、热、电IES为前提建立的,然而迁移学习理论也能够用于热、电耦合、电-热-气等多种形式的IES负荷预测中。后续工作将逐步研究并完善上述问题。
| [1] |
辛保安. 为实现"碳达峰、碳中和"目标贡献智慧和力量[N/OL]. 人民网, (2021-02-23)[2021-03-28]. http://finance.people.com.cn/n1/2021/0223/c1004-32034201.html. XIN Bao'an. Contribute wisdom and strength to achieve the goal of 'carbon peak, carbon neutral'[N/OL]. People's daily, (2021-02-23)[2021-03-28]. http://finance.people.com.cn/n1/2021/0223/c1004-32034201.html. (  0) 0) |
| [2] |
WANG Y L, WANG Y D, HUANG Y J, et al. Optimal scheduling of the regional integrated energy system considering economy and environment[J]. IEEE Transactions on Sustainable Energy, 2019, 10(4): 1939-1949. DOI:10.1109/TSTE.2018.2876498 (  0) 0) |
| [3] |
张宇帆, 艾芊, 林琳, 等. 基于深度长短时记忆网络的区域级超短期负荷预测方法[J]. 电网技术, 2019, 43(6): 1884-1892. ZHANG Yufan, AI Qian, LIN Lin, et al. A very short-term load forecasting method based on deep LSTM RNN at zone level[J]. Power System Technology, 2019, 43(6): 1884-1892. (  0) 0) |
| [4] |
李焱, 贾雅君, 李磊, 等. 基于随机森林算法的短期电力负荷预测[J]. 电力系统保护与控制, 2020, 48(21): 117-124. LI Yan, JIA Yajun, LI Lei, et al. Short term power load forecasting based on a stochastic forest algorithm[J]. Power System Protection and Control, 2020, 48(21): 117-124. (  0) 0) |
| [5] |
黄青平, 邹晓明, 刘楚群, 等. 基于小波分解与随机森林的短期负荷预测[J]. 电力信息与通信技术, 2019, 17(9): 24-29. HUANG Qingping, ZOU Xiaoming, LIU Chuqun, et al. Short term load forecasting based on wavelet decomposition and random forest[J]. Electric Power Information and Communication Technology, 2019, 17(9): 24-29. (  0) 0) |
| [6] |
乡立, 段炼, 陈菁, 等. 基于WEKPCA与深度学习的短期电力负荷预测[J]. 电力信息与通信技术, 2020, 18(10): 34-41. XIANG Li, DUAN Lian, CHEN Jing, et al. Short-term power load forecasting based on WEKPCA and deep learning[J]. Electric Power Information and Communication Technology, 2020, 18(10): 34-41. (  0) 0) |
| [7] |
邓带雨, 李坚, 张真源, 等. 基于EEMD-GRU-MLR的短期电力负荷预测[J]. 电网技术, 2020, 44(2): 593-602. DENG Daiyu, LI Jian, ZHANG Zhenyuan, et al. Short-term electric load forecasting based on EEMD-GRU-MLR[J]. Power System Technology, 2020, 44(2): 593-602. (  0) 0) |
| [8] |
蔡舒平, 闫静, 刘国海, 等. 基于Fisher信息和在线SVR的智能电网气象敏感负荷预测动态建模技术[J]. 中国电机工程学报, 2020, 40(11): 3441-3452. CAI Shuping, YAN Jing, LIU Guohai, et al. A dynamic modeling methodology based on Fisher information and on-line SVR for smart grids weather sensitive load forecasting[J]. Proceedings of the CSEE, 2020, 40(11): 3441-3452. (  0) 0) |
| [9] |
SINGH P, DWIVEDI P. A novel hybrid model based on neural network and multi-objective optimization for effective load forecast[J]. Energy, 2019, 182: 606-622. (  0) 0) |
| [10] |
石天, 梅飞, 陆继翔, 等. 基于PSR和DBN的超短期母线净负荷预测[J]. 电力工程技术, 2020, 39(1): 178-183. SHI Tian, MEI Fei, LU Jixiang, et al. Ultra-short-term bus net load forecasting based on phase space reconstruction and deep belief network[J]. Electric Power Engineering Technology, 2020, 39(1): 178-183. (  0) 0) |
| [11] |
HAO Z H, LIU G X, ZHANG H Y. Correlation filter-based visual tracking via adaptive weighted CNN features fusion[J]. IET Image Processing, 2018, 12(8): 1423-1431. (  0) 0) |
| [12] |
陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137. LU Jixiang, ZHANG Qipei, YANG Zhihong, et al. Short-term load forecasting method based on CNN-LSTM hybrid neural network model[J]. Automation of Electric Power Systems, 2019, 43(8): 131-137. (  0) 0) |
| [13] |
赵兵, 王增平, 纪维佳, 等. 基于注意力机制的CNN-GRU短期电力负荷预测方法[J]. 电网技术, 2019, 43(12): 4370-4376. ZHAO Bing, WANG Zengping, JI Weijia, et al. A short-term power load forecasting method based on attention mechanism of CNN-GRU[J]. Power System Technology, 2019, 43(12): 4370-4376. (  0) 0) |
| [14] |
栗然, 孙帆, 丁星, 等. 考虑多能时空耦合的用户级综合能源系统超短期负荷预测方法[J]. 电网技术, 2020, 44(11): 4121-4134. LI Ran, SUN Fan, DING Xing, et al. Ultra short-term load forecasting for user-level integrated energy system considering multi-energy spatio-temporal coupling[J]. Power System Technology, 2020, 44(11): 4121-4134. (  0) 0) |
| [15] |
马建鹏, 龚文杰, 张智晟. 基于Copula理论与KPCA-GRNN结合的区域综合能源系统多元负荷短期预测模型[J]. 电工电能新技术, 2020, 39(3): 24-31. MA Jianpeng, GONG Wenjie, ZHANG Zhisheng. Short-term multiple load prediction model for regional integrated energy system based on Copula theory and KPCA-GRNN[J]. Advanced Technology of Electrical Engineering and Energy, 2020, 39(3): 24-31. (  0) 0) |
| [16] |
田浩含, 张智晟, 于道林. 基于改进LSTM的区域综合能源系统多元负荷短期预测研究[J]. 电力系统及其自动化学报, 2021, 33(9): 130-137. TIAN Haohan, ZHANG Zhisheng, YU Daolin. Load short-term forecasting model of regional integrated energy system based on improved LSTM[J]. Proceedings of the CSU-EPSA, 2021, 33(9): 130-137. (  0) 0) |
| [17] |
TAN Z F, DE G, LI M L, et al. Combined electricity-heat-cooling-gas load forecasting model for integrated energy system based on multi-task learning and least square support vector machine[J]. Journal of Cleaner Production, 2020, 248: 119252. (  0) 0) |
| [18] |
孙庆凯, 王小君, 张义志, 等. 基于LSTM和多任务学习的综合能源系统多元负荷预测[J]. 电力系统自动化, 2021, 45(5): 63-70. SUN Qingkai, WANG Xiaojun, ZHANG Yizhi, et al. Multiple load prediction of integrated energy system based on long short-term memory and multi-task learning[J]. Automation of Electric Power Systems, 2021, 45(5): 63-70. (  0) 0) |
| [19] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. (  0) 0) |
| [20] |
WANG Jindong. Everything about transfer learning and domain adaptation[EB/OL]. [2021-06-02]. https://github.com/jindongwang/transferlearning.
(  0) 0) |
| [21] |
GHIFARY M, KLEIJN W B, ZHANG M. Domain adaptive neural networks for object recognition[C]//Pacific Rim Interna-tional Conference on Artificial Intelligence. Gold Coast, QLD, Australia: Springer International Publishing, 2014: 898-904.
(  0) 0) |
| [22] |
Open EI DOE open data[DB/OL]. [2021-06-02]. https://openei.org/doe-opendata/dataset.
(  0) 0) |
2. State Grid Jiangxi Electric Power Co., Ltd., Nanchang 330096, China

 何桂雄(1984), 男, 硕士, 高级工程师, 从事需求侧管理、综合能源优化技术相关工作(E-mail:
何桂雄(1984), 男, 硕士, 高级工程师, 从事需求侧管理、综合能源优化技术相关工作(E-mail: