文章编号: 2096-3203(2022)05-0058-09 中图分类号: TM73
2. 楚雄师范学院物理与电子科学学院, 云南 楚雄 675000;
3. 云南电网有限责任公司电力科学研究院,云南 昆明 650217
近年来,能源短缺、环境恶化现象日益严重,如何提高能源利用率,促进可再生能源最大消纳,是目前的研究热点[1—4]。热电联产(combined heat and power,CHP)系统具有热能、电能互补,错峰调节等优点,通过引入储能装置进行灵活调度[5],能够有效促进能源的高效利用,具有广阔的发展前景。
目前,众多学者对CHP系统的协调控制及优化运行展开了深入研究,文献[6]提出一种基于共享储能电站的工业用户日前优化经济调度方法,通过协调各用户使用共享储能电站进行充电和放电的功率,实现用户群日运行成本最优。文献[7]针对CHP系统,提出一种新型混合储能系统优化模型,该模型综合考虑了混合储能系统的荷电状态、电流和容量。
供热网络和热负荷作为CHP系统的重要组成部分,在提高系统性能方面具有很大潜力[8—9]。文献[10]建立忽略传输延迟的热网简化模型,研究了热网对区域多能源系统运行成本的影响,结果表明,利用热网可以降低系统的运行成本。文献[11]利用负荷侧建筑物储热能力,在风电出力前增加供热量,将一部分热量储存在建筑物和热管网中,实现了电力与热力的错峰调节。上述研究以电力能源为主体,重点关注电网调度及灵活供电,通过热网传输延时和热负荷蓄热参与系统调度,提高了能效。但系统控制过程中未考虑可再生能源出力及负荷波动对系统运行的影响。
针对可再生能源及负荷的波动性问题,文献[12—13]提出基于滚动优化的模型预测控制(model predictive control,MPC)方法,MPC算法通过反馈控制构成闭环系统,能够动态调节系统输出,其计算简单、控制效果好、鲁棒性强[14],被广泛应用于电力系统优化、能量管理等领域。文献[15]提出一种基于MPC算法的多时间尺度主动配电网多源协调优化调度策略,能够解决主动配电网中分布式电源出力预测精度随时间尺度增长而下降, 从而导致预测不准确的问题。文献[16]基于MPC算法,通过精细化协调控制和管理分布式电源、储能及柔性负荷,使有功出力控制过程更加平滑,但忽略了预测信息与实际运行信息之间存在的误差,导致供需不平衡。
鉴于上述研究存在的不足,文中针对并网运行状态下的CHP系统,综合考虑热电耦合机理、异质能特性、预测误差,提出考虑热惯性的两阶段协调优化调度策略。通过日内调度-实时调整两阶段协调配合,减小可再生能源出力和负荷的预测误差,不断完善系统调度计划,实现供需平衡;同时,降低可再生能源及负荷波动对系统的影响,进一步提高用能能效。
1 考虑热惯性的CHP系统建模首先研究CHP系统中核心设备的运行特性,建立详细数学模型,在此基础上,研究供热网络的传输特性及热负荷的热惯性,并建立热网与建筑供暖和生活热水模型,为实现CHP系统源-网-荷的纵向融合奠定基础。
1.1 CHP系统建模(1) 燃气轮机。燃气轮机的供电和供热模型为:
| $ \left\{\begin{array}{l} P_{\mathrm{gt}, t}=V_{\mathrm{gt}, t} H_{\mathrm{ng}} \eta_{\mathrm{gt}} \\ Q_{\mathrm{gt}, t}=\alpha P_{\mathrm{gt}, t} \end{array}\right. $ | (1) |
式中:Pgt, t,Qgt, t分别为t时刻燃气轮机输出的电功率和热功率;Vgt, t为t时刻燃气轮机的天然气消耗量;ηgt,Hng分别为燃气轮机的发电效率和天然气热值,其中Hng取值为9.78 kW ·h/m3;α为燃气轮机的热电比。
(2) 燃气锅炉。燃气锅炉模型为:
| $ Q_{\mathrm{gb}, t}=V_{\mathrm{gb}, t} H_{\mathrm{ng}} \eta_{\mathrm{gb}} $ | (2) |
式中:Qgb,t为t时刻燃气锅炉输出的热功率;Vgb,t为t时刻燃气锅炉的天然气消耗量;ηgb为燃气锅炉的发热效率。
(3) 蓄电池[17]。蓄电池模型为:
| $ E_{t+1}^{\mathrm{bt}}=E_t^{\mathrm{bt}}+\left(\eta_{\mathrm{bt}, \mathrm{chr}} P_t^{\mathrm{bt}, \mathrm{chr}}-P_t^{\mathrm{bt} , \mathrm{dis}} / \eta_{\mathrm{bt}, \mathrm{dis}}\right) \Delta t $ | (3) |
式中:Et+1bt为t+1时刻蓄电池存储的电量;Ptbt, chr,Ptbt, dis分别为t时刻蓄电池的充、放电功率;ηbt, chr,ηbt, dis分别为蓄电池的充、放电效率;Δt为时间间隔。
(4) 蓄热槽[17]。蓄热槽模型为:
| $ E_{t+1}^{\mathrm{tst}}=E_t^{\mathrm{tst}}+\left(\eta_{\mathrm{tst}, \mathrm{chr}} Q_t^{\mathrm{tst}, \mathrm{chr}}-Q_t^{\mathrm{tst}, \mathrm{dis}} / \eta_{\mathrm{tst}, \mathrm{dis}}\right) \Delta t $ | (4) |
式中:Et+1tst为t+1时刻蓄热槽存储的热量;Qttst, chr,Qttst, dis分别为t时刻蓄热槽的吸、放热功率;ηtst, chr,ηtst, dis分别为蓄热槽的吸、放热效率。
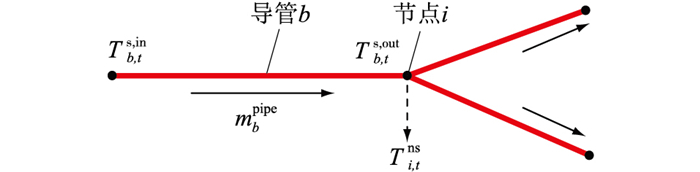
1.2 供热网络建模供热网络的简单结构如图 1所示,供热网络以热水为媒介传输热功率,其组成包括供水管道,回水管道和节点。供水管道与回水管道结构类似,因此图 1中省略了回水管道。
|
图 1 供热网结构 Fig. 1 Structure of the heating network |
图中Tb, ts, in,T b, ts, out分别为t时刻供水管道b入口、出口处的热水温度;mbpipe为管道b的质量流率;Ti, tns为供水节点i的热水温度。
文中供热网络的运行模式为质调节模式[18],质调节模式下,工质的流量保持恒定,而工质的温度与热量成正比。质调节模式考虑供热网络热力环节的改变,即工质水流在管道中传输延时的影响。文中假设供热网络供水温度和回水温度均为定值, 供热网络的约束包括节点温度融合与节点流量平衡、传输延时、热能损耗。
(1) 节点温度融合与节点流量平衡。节点温度融合模型为:
| $ \begin{cases}T_{b, t}^{\mathrm{s}, \text { out }}=T_{i, t}^{\mathrm{ns}} & \forall i \in I_{\mathrm{nd}} ; b \in \mathit{\Phi}_{+}^i ; t \in \bf{N} \\ T_{b, t}^{\mathrm{r}, \text { in }}=T_{j, t}^{\mathrm{nr}} & \forall j \in I_{\mathrm{nd}} ; b \in \mathit{\Phi}_{-}^j ; t \in \bf{N}\end{cases} $ | (5) |
式中:Tb, tr, in为t时刻回水管道b入口处的热水温度;Tj, tnr为t时刻回水节点j的热水温度;Ind为供热网络的节点集合;Φ+i为以节点i为起点的管道集合;Φ-j为以节点j为终点的管道集合。
节点流量平衡模型为:
| $ \left\{\begin{array}{l} Q_{\text {out }, t}^{\mathrm{co}}=c \sum\limits_{b \in \mathit{\Phi}_{\mathrm{src}}} m_b^{\mathrm{pipe}}\left(T_{b, t}^{\mathrm{s}, \text { in }}-T_{b, t}^{\mathrm{r}, \text { out }}\right) \\ Q_{i, t}^{\mathrm{hn}}=c m_b^{\mathrm{pipe}}\left(T_{b, t}^{\mathrm{s}, \text { out }}-T_{b, t}^{\mathrm{r}, \text { in }}\right) \\ \;\;\;\;\;\;\;\;b \in \mathit{\Phi}_i^{\mathrm{hl}} ; \forall i \in I_{\mathrm{nd}}^{\mathrm{hl}} \end{array}\right. $ | (6) |
式中:Qout, tco为t时刻CHP系统输出的热功率;c为水的比热容,取4.168 kJ/(kg·℃);Tb, tr, out为t时刻回水管道b出口处的热水温度;Qi, thn为t时刻节点i的热能需求;Φsrc为连接到源节点的管道集合;Φihl为连接到节点i的管道集合;Indhl为热负荷节点集合。
(2) 热能损耗及能量流模型。热能损耗及能量流模型为:
| $ \left\{\begin{array}{l} T_{b, t}^{\mathrm{s}, \text { out }}=T_t^{\mathrm{am}}+\left(T_{b, t}^{\mathrm{s} \text {, out }}-T_t^{\mathrm{am}}\right) \xi_b \\ T_{b, t}^{\mathrm{r}, \text { out }}=T_t^{\mathrm{am}}+\left(T_{b, t}^{\mathrm{r} \text {, out }}-T_t^{\mathrm{am}}\right) \xi_b \end{array}\right. $ | (7) |
| $ \xi_b=\exp \left(-\frac{\lambda_b \Delta t}{A_b \rho c}\left(\gamma_b+\frac{3}{2}+\frac{\rho A_b l_b-R_b}{m_b^{\text {pipe }} \Delta t}\right)\right) $ | (8) |
式中:Ttam为t时刻供热网络的环境温度;ξb为管道b热损系数;λb为管道b的传热系数;Ab为管道b的横截面积;ρ为水的密度;lb为管道b的长度;γb为管道b中热水水流的时间延时系数;Rb为从t-γb到t时刻管道b的总流量。
(3) 热量-流量等式。式(9)和式(10)为热水所带热能与热水流量以及热水温度模型。
| $ \left\{\begin{array}{l} Q_{b, t}^{\mathrm{s}, \text { in }}=m_b^{\mathrm{pipe}} c T_{b, t}^{\mathrm{s}, \text { in }} \quad b \in \mathit{\Phi}_i^{\mathrm{hl}} \\ Q_{b, t}^{\mathrm{s}, \text { out }}=m_b^{\mathrm{pipe}} c T_{b, t}^{\mathrm{s}, \text { out }} \quad b \in \mathit{\Phi}_i^{\mathrm{hl}} \end{array}\right. $ | (9) |
| $ \begin{cases}Q_{b, t}^{\mathrm{r}, \text { in }}=m_b^{\mathrm{pipe}} c T_{b, t}^{\mathrm{r}, \text { in }} & b \in \mathit{\Phi}_i^{\mathrm{hl}} \\ Q_{b, t}^{\mathrm{r}, \text { out }}=m_b^{\mathrm{pipe}} c T_{b, t}^{\mathrm{r}, \text { out }} &\;\; b \in \mathit{\Phi}_i^{\mathrm{hl}}\end{cases} $ | (10) |
式中:Qb, ts, in,Qb, ts, out分别为t时刻供水管道b入口处和出口处的热能;Qb, tr, in,Qb, tr, out分别为t时刻回水管道b入口处和出口处的热能。
(4) 温度约束。温度约束为:
| $ \left\{\begin{array}{l} T_{\min }^{\mathrm{s}} \leqslant T_{b, t}^{\mathrm{s}, \text { in }}, T_{b, t}^{\mathrm{s}, \text { out }} \leqslant T_{\max }^{\mathrm{s}} \\ T_{\min }^{\mathrm{r}} \leqslant T_{b, t}^{\mathrm{r}, \text { in }}, T_{b, t}^{\mathrm{r}, \text { out }} \leqslant T_{\max }^{\mathrm{r}} \end{array}\right. $ | (11) |
式中:Tmaxs,Tmins分别为供水管道热水温度上、下限;Tmaxr,Tminr分别为回水管道热水温度上、下限。
1.3 建筑供暖和生活热水建模建筑物供暖模型为:
| $ \begin{aligned} T_{i, t+1}^{\mathrm{in}}=& T_{i, t}^{\mathrm{in}} \times \exp \left(-\frac{\Delta t}{R_i C_i^{\mathrm{air}}}\right)+\left(\frac{R_i Q_{i, t}^{\mathrm{hl}, 1}}{B_i}+T_t^{\text {out }}\right) \times \\ &\left(1-\exp \left(-\frac{\Delta t}{R_i C_i^{\mathrm{air}}}\right)\right) \quad \forall i \in I_{\text {nd }}^{\mathrm{hl}} \end{aligned} $ | (12) |
式中:Ti, tin为t时刻热负荷节点i的室内温度;Ri为建筑物在热负荷节点i的热阻;Ciair为在热负荷节点i处的室内空气热容量;Bi为热负荷节点i处的建筑物数量;Qi, thl, 1为t时刻提供给负荷节点i用于建筑供暖的热功率;Ttout为t时刻的室外温度。
为了使供热质量保持在一个良好的水平,室内温度应该维持在一定范围之内,并且调度期间的平均值应该等于式(13)中给出的最佳值。
温度约束为:
| $ \left\{\begin{array}{l} T_{\min }^{\mathrm{w}} \leqslant T_{i, t}^{\mathrm{w}} \leqslant T_{\max }^{\mathrm{w}} \\ \sum\limits_{t \in \bf{N}} T_{i, t}^{\mathrm{w}}=N_{\mathrm{d}} T_{\mathrm{opt}}^{\mathrm{w}} \end{array}\right. $ | (13) |
式中:Tmaxw,Tminw分别为舒适水温的上、下限;Toptw为最佳水温;Nd为一天中的时间段数量。
热功率平衡模型为:
| $ Q_{i, t}^{\mathrm{hl}}=Q_{i, t}^{\mathrm{hi, 1}}+Q_{i, t}^{\mathrm{hl}, 2} $ | (14) |
式中:Qi, thl,Qi, thl, 2分别为t时段负荷节点i用户的总热负荷和生活热水负荷。
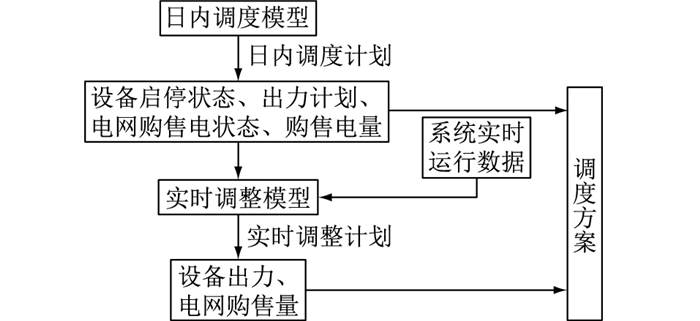
2 两阶段优化调度模型 2.1 两阶段优化框架为了降低可再生能源及负荷的波动性和不确定性对调度结果的影响,文中提出基于两阶段优化的调度模型,该模型包括日内调度阶段和日内实时调整阶段。日内调度阶段结合热惯性,基于MPC方法滚动优化日内可控设备的启停状态、出力计划及电网购售电状态、购售电量;日内实时调整阶段在日内调度计划出力的基础上协调各联供设备以调整量最小为目标,通过监测更新可再生能源及负荷的实时数据,不断调整设备出力和电网购售电量,最后确定调度方案。具体优化调度模型示意如图 2所示。
|
图 2 两阶段优化调度模型 Fig. 2 Two-stage optimal scheduling model |
由于可再生能源和负荷功率存在间歇性与随机性,导致实时数据难以预测。日内调度阶段是基于MPC的经济调度模型,其核心包含预测模型、滚动优化和反馈校正3个阶段,从而得到当前时段的调度计划。
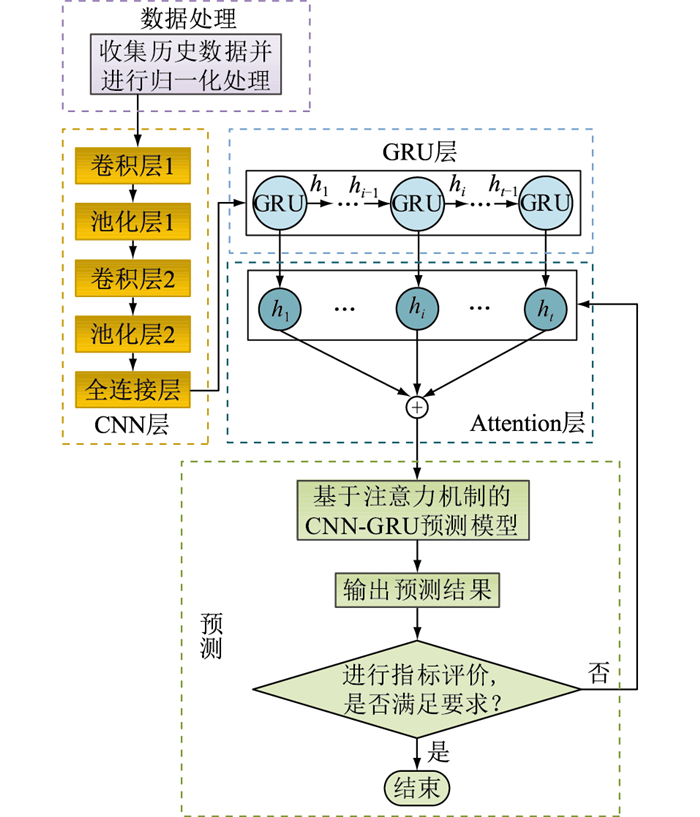
2.2.1 预测模型文中MPC的时效为15 min,属于短期预测(5~60 min),目前常用的短期预测方法有卡尔曼滤波、时间序列、灰色理论和回归分析法等,但在提取有效历史数据,防止重要信息丢失方面有一定局限性,因此文中采用文献[19]提出的基于注意力机制的卷积神经网络(convolutional neural network,CNN)和门控循环单元(gated recurrent unit,GRU)短期电力负荷预测方法。模型结构如图 3所示,具体步骤如下。
|
图 3 基于注意力机制的CNN-GRU模型结构 Fig. 3 Structure of CNN-GRU model based on attention mechanism |
步骤1:对历史负荷数据归一化处理,将其作为CNN模型的输入量。
步骤2:使用CNN提取历史负荷数据特征,并构造时间序列作为GRU模型的输入量。
步骤3:GRU层学习CNN层提取的数据特征向量,以捕获其内部变化的规律。
步骤4:Attention层结合GRU层的输出量和权重分配原则迭代更新得到较优的权重参数矩阵。
步骤5:建立较优的基于注意力机制的CNN-GRU预测模型并进行预测,输出预测结果,结合评价指标综合评价,如不满足评价要求则返回步骤4。
2.2.2 反馈校正在目前风电、光伏的预测精度下,超前的MPC无法保证风电、光伏出力与预测值相同,导致超前下发的可控分布式电源出力与实际有功出力之间存在偏差。因此需要反馈校正环节,以系统当前实际的有功出力值为新一轮滚动优化调度的初始值,构成闭环控制,克服系统及风电、光伏的不确定性,使新一轮的有功出力预测值更加贴合实际,精度更高。文中采用均方根相对误差对预测结果进行评估,如果拟合精度小于或等于0.05,则输出预测序列;如果拟合精度大于0.05,则计算残差序列,预测误差加权值来修正下一次的预测序列。
2.2.3 滚动优化滚动优化环节利用反馈校正后的预测数据对日内调度计划进行修正,同时指导下一时段调度计划。滚动优化过程是在时刻k,以[k, k+M]时段内的系统运行成本最小为优化目标建立模型并求解,求解结果只取第一个时刻的调度计划执行,到了k+1时刻,时间窗口向后移一个,再重复上述过程。
(1) 目标函数为:
| $ \min F=\sum\limits_{t=k}^{k+M}\left(F_{\text {fuel }}+F_{\text {grid }}+F_{\text {main }}\right) $ | (15) |
其中:
| $ F_{\text {fuel }}=f_{\mathrm{gas}}\left(\sum\limits_{t \in \bf{N}} \frac{P_{\mathrm{gt}, t}}{\eta_{\mathrm{gt}}}-\sum\limits_{t \in \bf{N}} \frac{Q_{\mathrm{gb}, t}}{\eta_{\mathrm{gb}}}\right) \Delta t_1 $ | (16) |
| $ F_{\text {grid }}=\left(\sum\limits_{t \in \bf{N}} f_{\text {grid }, \mathrm{b}} P_t^{\text {grid }, \mathrm{b}}-\sum\limits_{t \in \bf{N}} f_{\text {grid }, \mathrm{s}} P_t^{\text {grid }, \mathrm{s}}\right) \Delta t_1 $ | (17) |
| $ \begin{gathered} F_{\text {main }}=\sum_{t \in \mathrm{N}}\left(f_{\mathrm{om}}^{\mathrm{gt}} P_{\mathrm{gt}, t}+f_{\mathrm{om}}^{\mathrm{gb}} Q_{\mathrm{gb}, t}+f_{\mathrm{om}}^{\mathrm{bt}} P_t^{\mathrm{bt}, \mathrm{chr}}+\right. \\ \left.f_{\mathrm{om}}^{\mathrm{bt}} P_t^{\mathrm{bt}, \text { dis }}+f_{\mathrm{om}}^{\mathrm{tst}} Q_t^{\mathrm{tst}, \mathrm{chr}}+f_{\mathrm{om}}^{\mathrm{tst}} Q_t^{\mathrm{tst}, \text { dis }}\right) \end{gathered} $ | (18) |
式中:F为系统运行的总成本;Ffuel为燃料成本;Fgrid为与电网的交互功率成本;Fmain为运行维护成本;fgas为天然气价格,取值为2.3元/m3;fgrid, b,fgrid, s分别为购、售电价格;Ptgrid, b,Ptgrid, s分别为t时刻从主电网购、售电量;fomgt,fomgb,fombt,fomtst分别为燃气轮机、燃气锅炉、蓄电池、蓄热槽的单位容量运行维护成本;M为滚动优化的调度控制时域,取值为4 h[19—20];Δt1为日内调度阶段的时间间隔,取值为15 min。
(2) 约束条件。燃气轮机与燃气锅炉上下限约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{gt}, t} \leqslant P_{\mathrm{gt}, \text { cap }} \\ 0 \leqslant Q_{\mathrm{gb}, t} \leqslant Q_{\mathrm{gb}, \text { cap }} \end{array}\right. $ | (19) |
式中:Pgt, cap,Qgb, cap分别为燃气轮机和燃气锅炉容量。
蓄电池运行约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_t^{\mathrm{bt}, \mathrm{chr}} \leqslant \varepsilon_t^{\mathrm{bt}, \mathrm{chr}} \lambda_{\mathrm{chr}}^{\mathrm{bt}} E_{\mathrm{cap}}^{\mathrm{bt}} \\ 0 \leqslant P_t^{\mathrm{bt}, \mathrm{dis}} \leqslant \varepsilon_t^{\mathrm{bt}, \mathrm{dis}} \lambda_{\mathrm{dis}}^{\mathrm{bt}} E_{\mathrm{cap}}^{\mathrm{bt}} \\ \varepsilon_t^{\mathrm{bt}, \mathrm{chr}}+\varepsilon_t^{\mathrm{bt}, \mathrm{dis}} \leqslant 1 \\ E_{t+1}^{\mathrm{bt}}=E_t^{\mathrm{bt}}+\left(\eta_{\mathrm{bt}, \mathrm{chr}} P_t^{\mathrm{bt}, \mathrm{chr}}-P_t^{\mathrm{bt}, \mathrm{dis}} / \eta_{\mathrm{bt}, \mathrm{dis}}\right) \Delta t_1 \\ \pi_{\mathrm{low}}^{\mathrm{bt}} E_{\mathrm{cap}}^{\mathrm{bt}} \leqslant E_t^{\mathrm{bt}} \leqslant \pi_{\mathrm{up}}^{\mathrm{bt}} E_{\mathrm{cap}}^{\mathrm{bt}} \end{array}\right. $ | (20) |
式中:Ecapbt为蓄电池容量;εtbt, chr,εtbt, dis分别为t时刻蓄电池充、放电状态标记位,为0-1变量,εtbt, chr=1表示蓄电池正在充电;λchrbt,λdisbt分别为蓄电池充、放电功率的最大倍率;πupbt,πlowbt分别为蓄电池蓄电状态值的上、下限系数。
蓄热槽与蓄电池在CHP系统中功能类似,蓄热槽运行约束为:
| $ \left\{\begin{array}{l} 0 \leqslant Q_t^{\mathrm{tst}, \mathrm{chr}} \leqslant \varepsilon_t^{\mathrm{ts}, \mathrm{chr}} \lambda_{\mathrm{chr}}^{\mathrm{tst}} E_{\mathrm{cap}}^{\mathrm{tst}} \\ 0 \leqslant Q_t^{\mathrm{tst}, \mathrm{dis}} \leqslant \varepsilon_t^{\mathrm{tst}, \mathrm{dis}} \lambda_{\mathrm{dis}}^{\mathrm{tst}} E_{\mathrm{cap}}^{\mathrm{tst}} \\ \varepsilon_t^{\mathrm{tst}, \mathrm{chr}}+\varepsilon_t^{\mathrm{tst}, \mathrm{dis}} \leqslant 1 \\ E_{t+1}^{\mathrm{tst}}=E_t^{\mathrm{tst}}+\left(\eta_{\mathrm{tst}, \mathrm{chr}} Q_t^{\mathrm{tst}, \mathrm{chr}}-Q_t^{\mathrm{tst}, \mathrm{dis}} / \eta_{\mathrm{tst}, \mathrm{dis}}\right) \Delta t_1 \\ \pi_{\mathrm{low}}^{\mathrm{tst}} E_{\mathrm{cap}}^{\mathrm{tst}} \leqslant E_t^{\mathrm{tst}} \leqslant \pi_{\mathrm{up}}^{\mathrm{tst}} E_{\mathrm{cap}}^{\mathrm{tst}} \end{array}\right. $ | (21) |
式中:Ecaptst为蓄热槽容量;εttst, chr,εttst, dis分别为t时刻蓄热槽吸热、放热状态标记位,为0-1变量,εttst, chr=1表示蓄热槽为吸热状态;λchrtst,λdistst分别为蓄热槽吸热功率和放热功率的最大倍率;πuptst,πlowtst分别为蓄热槽蓄热状态值的上、下限系数。
系统与主电网约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_t^{\text {grid, } \mathrm{b}} \leqslant \varepsilon_t^{\text {grid, b }} P_{\text {max }}^{\text {grid }} \\ 0 \leqslant P_t^{\text {grid, }} \leqslant \varepsilon_t^{\text {grid, s }} P_{\text {max }}^{\text {grid }} \\ \varepsilon_t^{\text {grid, b }}+\varepsilon_t^{\text {grid, }} \leqslant 1 \end{array}\right. $ | (22) |
式中:Pmaxgrid为与电网的最大交互功率;εtgrid, b,εtgrid, s分别为电网购、售电的状态标记位,为0-1变量,εtgrid, b=1表示系统购电。
能量传输约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_{t, \text { in }}^{\text {load }} \leqslant \varepsilon_{t, \text { in }}^{\text {load }} P_{t, \text { tra }}^{\text {load }} \\ 0 \leqslant P_{t, \text { out }}^{\text {load }} \leqslant \varepsilon_{t, \text { out }}^{\text {load }} P_{t, \text { tra }}^{\text {load }} \\ \varepsilon_{t, \text { in }}^{\text {load }}+\varepsilon_{t, \text { out }}^{\text {load }}=1 \end{array}\right. $ | (23) |
式中:Pt, inload,Pt, outload分别为t时刻输入和输出的能量;εt, inload,εt, outload分别为能量在t时刻输入和输出的状态标记位,为0-1变量,εt, inload=1表示输入能量;Pt, traload为t时刻可传输的电功率。
系统能量平衡约束为:
| $ \left\{\begin{array}{l} P_{\mathrm{gt}, t}-P_t^{\mathrm{bt}, \mathrm{chr}}+P_t^{\mathrm{bt}, \mathrm{dis}}+P_t^{\mathrm{grid}, \mathrm{b}}-P_t^{\mathrm{grid}, \mathrm{s}}= \\ \;\;\;\;\;\;\;\;\;\;\;\;P_{\mathrm{fix}, t}^{\mathrm{load}}+P_{t, \text { in }}^{\mathrm{load}}-P_{t, \text { out }}^{\mathrm{load}} \\ Q_{\mathrm{gt}, t}+Q_{\mathrm{gb}, t}-Q_t^{\mathrm{tst}, \text { chr }}+Q_t^{\mathrm{tst}, \text { dis }}=Q_{\text {out }, t}^{\mathrm{co}} / \eta_{\mathrm{he}} \end{array}\right. $ | (24) |
式中:Pfix, tload为t时刻CHP系统的电负荷;ηhe为热交换器的效率。
通过求解基于MPC的日内调度阶段,得到各可控联供设备及蓄电池、蓄热槽未来的出力计划值。
2.3 日内实时调整阶段虽然滚动优化减少了可再生能源出力及负荷波动性和随机性的影响,但预测误差及超前的预测控制过程使优化方案与系统的实际值出现偏差,从而导致系统的经济性下降。引入实时调整阶段进行超短时效的可再生能源出力及负荷调度,以减小预测误差及预测模型对预测值的影响。实时调整每5 min执行一次,在日内调度阶段主要联供设备出力计划值的基础上调整其出力,该阶段以最小化设备调整量为目标。
(1) 目标函数为:
| $ \begin{gathered} \min D=\omega_1\left(\left|\Delta P_{\mathrm{grid}, \mathrm{b}}^{\mathrm{R}}\right| / P_{\mathrm{grid}, \mathrm{b}}^{\max }+\left|\Delta P_{\mathrm{grid}, \mathrm{s}}^{\mathrm{R}}\right| / P_{\mathrm{grid}, \mathrm{s}}^{\max }+\right. \\ \left.\left|\Delta P_{\mathrm{gt}}^{\mathrm{R}}\right| / P_{\mathrm{gt}}^{\max }+\left|\Delta P_{\mathrm{bt}, \mathrm{chr}}^{\mathrm{m}}\right| / P_{\mathrm{bt}, \mathrm{chr}}^{\max }+\left|\Delta P_{\mathrm{bt}, \mathrm{dis}}^{\mathrm{R}}\right| / P_{\mathrm{bt}, \mathrm{dis}}^{\max }\right)+ \\ \omega_2\left(\left|\Delta Q_{\mathrm{gb}}^{\mathrm{R}}\right| / Q_{\mathrm{gb}}^{\max }+\left|\Delta Q_{\mathrm{st}, \mathrm{chr}}^{\mathrm{R}}\right| / Q_{\mathrm{tst}, \mathrm{chr}}^{\max }+\right. \\ \left.\left|\Delta Q_{\mathrm{tst}, \mathrm{dis}}^{\mathrm{R}}\right| / Q_{\mathrm{tst}, \mathrm{dis}}^{\max }\right) \end{gathered} $ | (25) |
式中:D为系统总调整量;ΔPgrid, bR,ΔPgrid, sR,ΔPgtR,ΔPbt, chrR,ΔPbt, disR,ΔQgbR,ΔQtst, chrR,ΔQtst, disR分别为系统与电网交互功率,燃气轮机输出电功率,蓄电池充、放电功率,燃气锅炉输入热功率,蓄热槽吸、放热功率在实时调整阶段的调整量;ω1,ω2为电热功率调整权重系数,且ω1+ω2=1。
(2) 约束条件。燃气锅炉与燃气轮机上下限约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{gt}, t}+\Delta P_{\mathrm{gt}}^{\mathrm{R}} \leqslant P_{\mathrm{gt}, \text { cap }} \\ 0 \leqslant Q_{\mathrm{gb}, t}+\Delta Q_{\mathrm{gb}}^{\mathrm{R}} \leqslant Q_{\mathrm{gb}, \text { cap }} \end{array}\right. $ | (26) |
蓄电池运行约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_t^{\mathrm{bt}, \mathrm{chr}}+\Delta P_{\mathrm{bt}, \mathrm{chr}}^{\mathrm{R}} \leqslant \varepsilon_t^{\mathrm{bt}, \mathrm{chr}} \lambda_{\text {chr }}^{\mathrm{bt}} E_{\text {cap }}^{\mathrm{bt}} \\ 0 \leqslant P_t^{\mathrm{bt}, \mathrm{dis}}+\Delta P_{\mathrm{bt}, \mathrm{dis}}^{\mathrm{R}} \leqslant \varepsilon_t^{\mathrm{bt}, \text { dis }} \lambda_{\mathrm{dis}}^{\mathrm{bt}} E_{\mathrm{cap}}^{\mathrm{bt}} \\ \varepsilon_t^{\mathrm{bt}, \mathrm{chr}}+\varepsilon_t^{\mathrm{bt}, \text { dis }} \leqslant 1 \\ E_{t+1}^{\mathrm{bt}}=E_t^{\mathrm{bt}}+\left[\eta_{\mathrm{bt}, \mathrm{chr}}\left(P_t^{\mathrm{bt}, \text { chr }}+\Delta P_{\mathrm{bt}, \mathrm{chr}}^{\mathrm{R}}\right)-\right. \\ \;\;\;\;\;\left.\quad\left(P_t^{\mathrm{bt}, \mathrm{dis}}+\Delta P_{\mathrm{bt}, \mathrm{dis}}^{\mathrm{R}}\right) / \eta_{\mathrm{bt}, \mathrm{dis}}\right] \Delta t_2 \\ \pi_{\mathrm{low}}^{\mathrm{bt}} E_{\text {cap }}^{\mathrm{bt}} \leqslant E_t^{\mathrm{bt}} \leqslant \pi_{\mathrm{up}}^{\mathrm{bt}} E_{\text {cap }}^{\mathrm{bt}} \end{array}\right. $ | (27) |
式中:Δt2为实时调整阶段的时间间隔,取值为5 min。
蓄热槽运行约束为:
| $ \left\{\begin{array}{l} 0 \leqslant Q_t^{\mathrm{tst}, \mathrm{chr}}+\Delta Q_{\mathrm{tst}, \mathrm{chr}}^{\mathrm{R}} \leqslant \varepsilon_t^{\mathrm{tst}, \mathrm{chr}} \lambda_{\mathrm{chr}}^{\mathrm{tst}} E_{\mathrm{cap}}^{\mathrm{tst}} \\ 0 \leqslant Q_t^{\mathrm{tst}, \mathrm{dis}}+\Delta Q_{\mathrm{tst}, \mathrm{dis}}^{\mathrm{R}} \leqslant \varepsilon_t^{\mathrm{tst}, \mathrm{dis}} \lambda_{\mathrm{dis}}^{\mathrm{tst}} E_{\text {cap }}^{\mathrm{tst}} \\ \varepsilon_t^{\mathrm{tst}, \mathrm{chr}}+\varepsilon_t^{\mathrm{tst}, \mathrm{dis}} \leqslant 1 \\ E_{t+1}^{\mathrm{tst}}=E_t^{\mathrm{tst}}+\left[\eta_{\mathrm{tst}, \mathrm{chr}}\left(Q_t^{\mathrm{tst}, \mathrm{chr}}+\Delta Q_{\mathrm{tst}, \mathrm{chr}}^{\mathrm{R}}\right)-\right. \\ \;\;\;\;\;\left.\quad\left(Q_t^{\mathrm{tst}, \mathrm{dis}}+\Delta Q_{\mathrm{tst}, \mathrm{dis}}^{\mathrm{R}}\right) / \eta_{\mathrm{tst}, \mathrm{dis}}\right] \Delta t_2 \\ \pi_{\text {low }}^{\mathrm{tst}} E_{\text {cap }}^{\mathrm{tst}} \leqslant E_t^{\mathrm{tst}} \leqslant \pi_{\mathrm{up}}^{\mathrm{tst}} E_{\text {cap }}^{\mathrm{tst}} \end{array}\right. $ | (28) |
系统与电网的交互功率约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_t^{\text {grid, } \mathrm{b}}+\Delta P_{\text {grid, b }}^{\mathrm{R}} \leqslant \varepsilon_t^{\text {grid, b }} P_{\max }^{\text {grid }} \\ 0 \leqslant P_t^{\text {grid }, \mathrm{s}}+\Delta P_{\text {grid, } \mathrm{s}}^{\mathrm{R}} \leqslant \varepsilon_t^{\text {grid, }, \mathrm{s}} P_{\max }^{\text {grid }} \\ \varepsilon_t^{\text {grid, b }}+\varepsilon_t^{\text {grid, } \mathrm{s}} \leqslant 1 \end{array}\right. $ | (29) |
能量传输约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_{t, \text { in }}^{\text {load }}+\Delta P_{\mathrm{R}, \text { in }}^{\text {load }} \leqslant \varepsilon_{t, \text { in }}^{\text {load }} P_{t, \text { tra }}^{\text {load }} \\ 0 \leqslant P_{t, \text { out }}^{\text {load }}+\Delta P_{\mathrm{R}, \text { out }}^{\text {load }} \leqslant \varepsilon_{t, \text { out }}^{\text {load }} P_{t, \text { tra }}^{\text {load }} \\ \varepsilon_{t, \text { in }}^{\text {load }}+\varepsilon_{t, \text { out }}^{\text {load }}=1 \end{array}\right. $ | (30) |
式中:ΔPR, inload,ΔPR, outload分别为系统输入、输出电负荷在实时调整阶段的调整量。
热电能量平衡约束为:
| $ \left\{\begin{array}{l} \left(P_{\mathrm{gt}, \mathrm{t}}+\Delta P_{\mathrm{gt}}^{\mathrm{R}}\right)-\left(P_t^{\mathrm{bt}, \mathrm{chr}}+\Delta P_{\mathrm{bt}, \mathrm{chr}}^{\mathrm{R}}\right)+\left(P_t^{\mathrm{bt}, \text { dis }}+\right. \\ \left.\Delta P_{\mathrm{bt}, \mathrm{dis}}^{\mathrm{R}}\right)+\left(P_t^{\text {grid, b }}+\Delta P_{\mathrm{grid}, \mathrm{b}}^{\mathrm{R}}\right)-\left(P_t^{\text {grid, }, \mathrm{s}}+\Delta P_{\mathrm{grid}, \mathrm{s}}^{\mathrm{R}}\right)= \\ \;\;\;\;P_{D, \text { fix }}^{\text {load }}+\left(P_{t, \text { in }}^{\text {load }}+\Delta P_{\mathrm{R}, \text { in }}^{\text {load }}\right)-\left(P_{t, \text { out }}^{\text {load }}+\Delta P_{\mathrm{R}, \text { out }}^{\text {load }}\right) \\ \left(Q_{\mathrm{gt}, \mathrm{t}}+\Delta Q_{\mathrm{gt}}^{\mathrm{R}}\right)+\left(Q_{\mathrm{gb}, \mathrm{t}}+\Delta Q_{\mathrm{gb}}^{\mathrm{R}}\right)- \\ \;\;\;\;\left(Q_t^{\mathrm{tst}, \text { chr }}+\Delta Q_{\mathrm{tst}, \mathrm{chr}}^{\mathrm{R}}\right)+\left(Q_t^{\mathrm{tst}, \text { dis }}+\Delta Q_{\mathrm{tst}, \text { dis }}^{\mathrm{R}}\right)= \\ \;\;\;\;\quad\left(Q_t^{\mathrm{co}, \text { out }}+\Delta Q_{\mathrm{co}, \text { out }}^{\mathrm{R}}\right) / \eta_{\mathrm{he}} \end{array}\right. $ | (31) |
式中:PD, fixload为CHP系统的电负荷在实时调整阶段的调整量;ΔQgtR,ΔQco, outR分别为燃气轮机和CHP系统输出热功率在实时调整阶段的调整量。
通过对实时调度阶段求解,得到各可控联供设备及蓄电池、蓄热槽的调整功率。
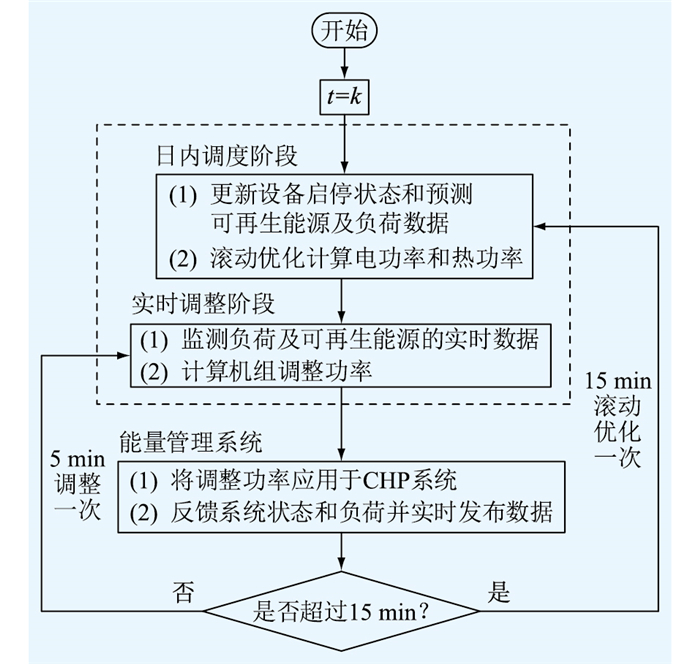
2.4 两阶段调度策略考虑热惯性的CHP系统两阶段优化调度控制流程如图 4所示。
|
图 4 两阶段优化控制框架 Fig. 4 Two-stage optimization control framework |
优化步骤如下:
步骤1:在每一个调度时段内,根据步骤6更新的可再生能源及负荷数据,预测未来4 h内可再生能源及负荷数据,并更新设备运行状态。
步骤2:对比预测序列与原始序列,计算预测误差加权值,修正下一次的预测序列。
步骤3:由步骤2得到的预测信息滚动优化得出未来4 h的调度计划,仅执行第一个15 min调度计划。
步骤4:监测可再生能源和负荷的实时数据,计算调整功率,反馈给能量管理系统。
步骤5:每5 min调整一次上一阶段的出力计划。
步骤6:如果超过15 min,反馈设备运行状态和负荷数据到步骤1。
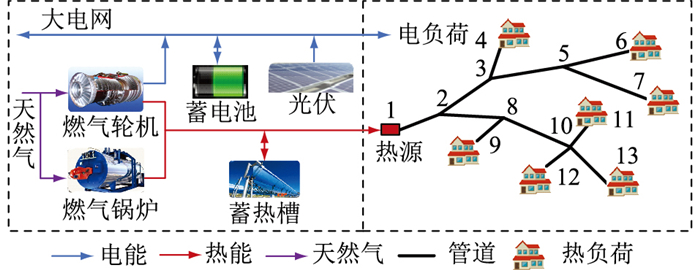
3 算例分析 3.1 系统结构和参数为了验证所提模型的有效性,选取中国北方某地区的热电负荷数据、电价信息等进行仿真,CHP系统相关参数见表 1—表 3,结构拓扑如图 5所示。整个地区配置如下:1台4 000 kW燃气轮机、1台4 500 kW燃气锅炉、1台2 000 kW蓄电池、1台2 500 kW蓄热槽、1台2 000 kW热交互器,热网部分包括12条热网传输管道和7个热负荷节点。日内调度阶段中模型预测控制的时效Δt1为15 min,控制时长取15 min(假设预测时长与控制时长相等)。实时调整阶段的调度时长为5 min,选择3个季节夏季80 d、冬季150 d和过渡季节135 d进行仿真(功率优化结果分析部分侧重于冬季的数据)。
|
|
表 1 CHP系统设备参数 Table 1 Parameters of devices in the CHP system |
|
|
表 2 热网参数 Table 2 Parameters of heating network |
|
|
表 3 热负荷参数 Table 3 Parameters of heating load |
|
图 5 CHP系统和热网结构 Fig. 5 Structure of the CHP system and the heating network |
为了分析两阶段优化和热网特性及热惯性对CHP系统运行经济性的影响,设计了4个案例:案例Ⅰ为传统案例,不考虑两阶段优化和热网特性及热惯性;案例Ⅱ在案例Ⅰ的基础上仅考虑热网特性及热惯性;案例Ⅲ在案例Ⅰ的基础上采用两阶段优化策略;案例Ⅳ为文中所提调度方法。4种案例CHP系统的运行成本如表 4所示。
|
|
表 4 系统的运行成本 Table 4 Operating cost of the system |
由表 4可知,与其他案例相比,案例Ⅳ经济性最优,说明采用两阶段优化或考虑热网特性及热惯性都能降低CHP系统运行成本。冬季系统运行的经济性明显提高,这是因为冬季热负荷需求较大,热网特性及热惯性对运行成本的影响更为明显,而通过两阶段优化方法降低运行成本不受季节限制。
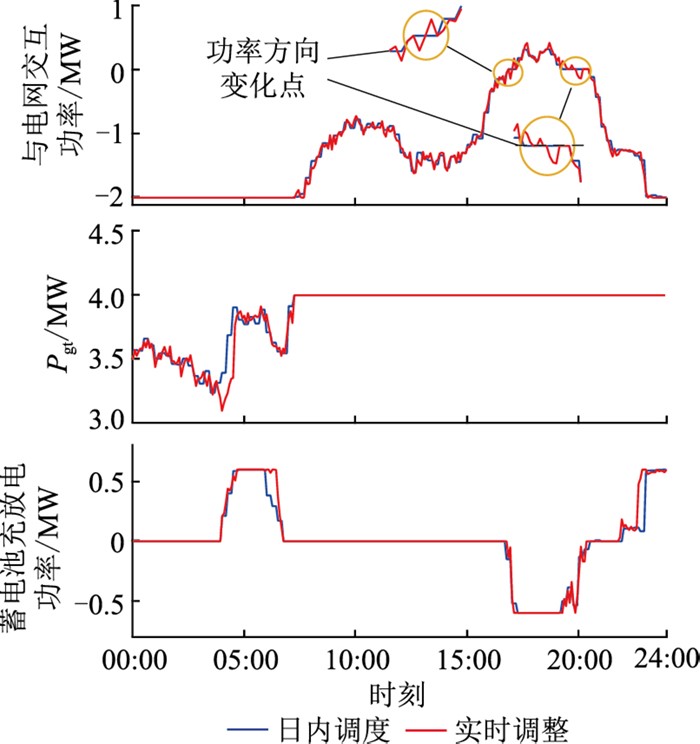
3.3 优化结果分析 3.3.1 电网功率优化结果分析CHP系统冬季典型日的主要设备输出电功率如图 6、图 7所示。其中,图 6为不考虑系统热惯性的两阶段功率优化结果;图 7为考虑系统热惯性的两阶段功率优化结果。两阶段内的运行优化结果包括与电网交互功率的优化结果、燃气轮机输出电功率的优化结果和蓄电池充放电功率优化结果。
|
图 6 不考虑热惯性的功率优化结果 Fig. 6 Power optimization results without considering thermal inertia |
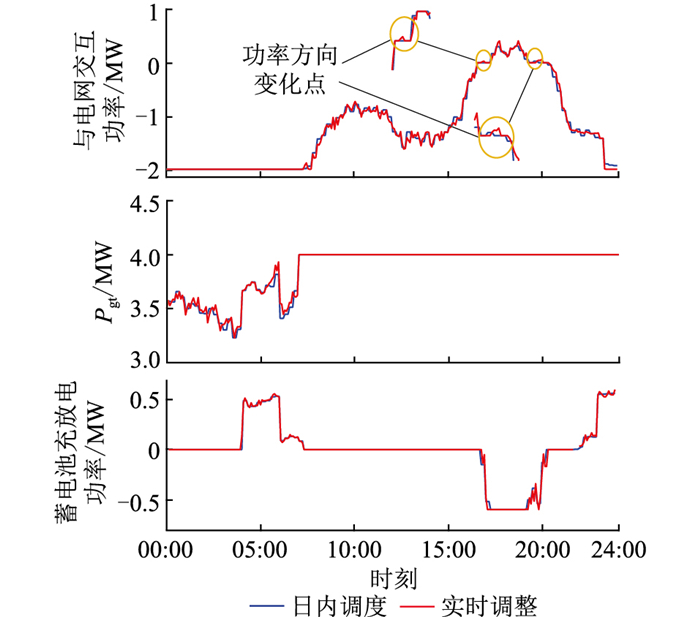
|
图 7 考虑热惯性的功率优化结果 Fig. 7 Power optimization results considering thermal inertia |
从图 6、图 7可以看出,冬季气温较低,燃气轮机持续运行保证系统对电、热能的供给。在00:00—09:00,系统与电网交互功率为负,期间负荷需求低, 说明系统向电网出售大量的电能,获得经济收益;在04:00—07:00,蓄电池的功率为正,表明蓄电池在充电, 而在16:00—20:00,系统与电网交互功率为正,燃气轮机满载运行,蓄电池功率为负,这是因为此时段内系统负荷需求增加,燃气轮机发电无法满足电负荷系统购电,需要向电网购电和投入蓄电池来保证系统电功率平衡。同时也可以看出,设备实时调整后的出力计划紧紧围绕日内调度计划波动,这是因为实时调整阶段通过建立精细化的调度模型减小了日内调度阶段可能存在的预测误差,弥补了一定范围内的供需不平衡。
与图 6相比,从图 7可以看出,在16:00—17:00、19:00—20:00,系统与电网交互功率方向发生了变化,这是因为交互功率的方向主要取决于负荷需求的波动,结合系统的热惯性后,当负荷需求减小时,热能被存储在建筑物中,反之热能被释放,从而减小系统与电网交互功率的波动。
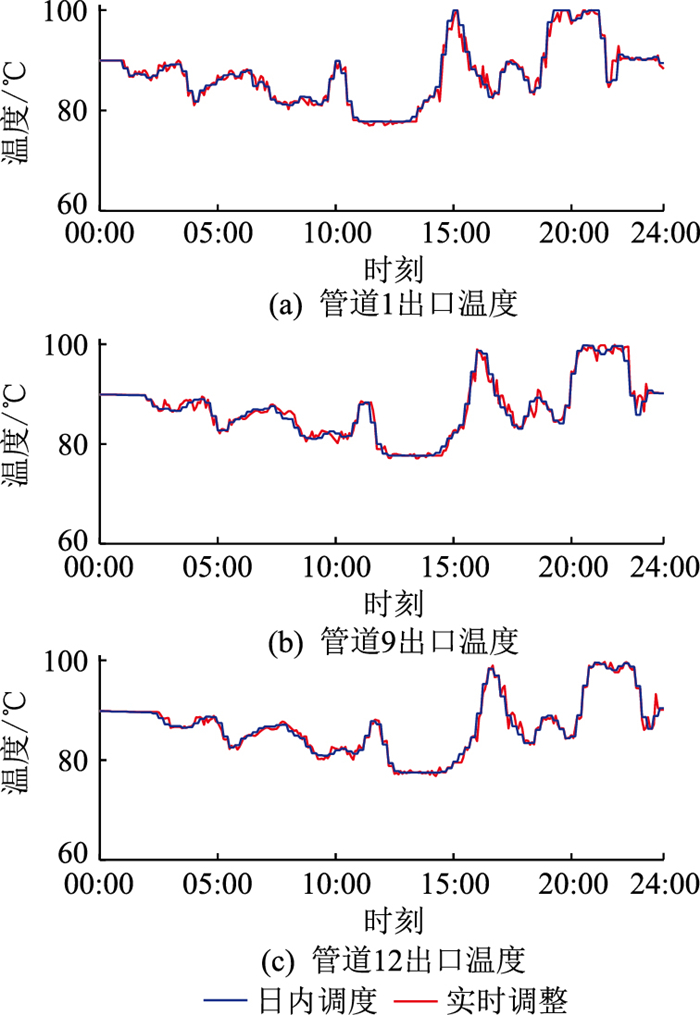
3.3.2 水温优化结果分析管道1、9、12出口温度变化如图 8所示。由图可以看出,每段管道的温度变化规律相似,但在时间上有所平移,这是因为热网的传输存在延时,离热源越远,延时越明显。此外,电价低谷时,供水温度较高;电价高峰时,供水温度降低,这说明建筑物根据分时电价蓄热或放热,促进了热能、电能互补。
|
图 8 两阶段内管道1、9、12出口温度变化 Fig. 8 Variation of temperature at the outlet of pipe 1, 9 and 12 in two stages |
针对电、热在传输和存储方式上的不同特性,文中提出一种考虑热惯性的CHP系统两阶段优化调度方法。主要结论为:
(1) 考虑热惯性的两阶段优化调度方法能提高系统运行的经济性,其中冬季典型日提高较为明显;
(2) 通过日内调度-实时调整两阶段优化方法,可以完善调度计划,弥补一定范围内的供需不平衡;
(3) 结合系统热惯性,建筑物根据负荷需求、分时电价进行蓄热或放热,能够平抑功率波动,促进热电互补。
但是文中建立的考虑热惯性的两阶段优化调度模型忽略了可再生能源波动性对热网运行的影响。此外,建立考虑供冷系统和天然气系统动态特性的调度模型对系统优化运行起到的积极作用有待进一步研究完善。
本文得到云南电网有限责任公司科技项目(YNKJXM20190087)资助,谨此致谢!
| [1] |
RIFKIN J. The third industrial revolution: how lateral power is transforming energy, the economy, and the world[M]. New York: Palgrave Macmillan, 2011.
(  0) 0) |
| [2] |
王伟亮, 王丹, 贾宏杰, 等. 能源互联网背景下的典型区域综合能源系统稳态分析研究综述[J]. 中国电机工程学报, 2016, 36(12): 3292-3306. WANG Weiliang, WANG Dan, JIA Hongjie, et al. Review of steady-state analysis of typical regional integrated energy system under the background of energy Internet[J]. Proceedings of the CSEE, 2016, 36(12): 3292-3306. (  0) 0) |
| [3] |
孙宏斌, 郭庆来, 吴文传, 等. 面向能源互联网的多能流综合能量管理系统: 设计与应用[J]. 电力系统自动化, 2019, 43(12): 122-128, 171. SUN Hongbin, GUO Qinglai, WU Wenchuan, et al. Integrated energy management system with multi-energy flow for energy Internet: design and application[J]. Automation of Electric Power Systems, 2019, 43(12): 122-128, 171. (  0) 0) |
| [4] |
朱罡, 王茂春. 含新能源发电的电力系统状态估计研究[J]. 电网与清洁能源, 2020, 36(4): 32-40, 47. ZHU Gang, WANG Maochun. Review on state estimation for power system containing renewable energy generation[J]. Power System and Clean Energy, 2020, 36(4): 32-40, 47. (  0) 0) |
| [5] |
黄仁乐, 蒲天骄, 刘克文, 等. 城市能源互联网功能体系及应用方案设计[J]. 电力系统自动化, 2015, 39(9): 26-33, 40. HUANG Renle, PU Tianjiao, LIU Kewen, et al. Design of hierarchy and functions of regional energy Internet and its demonstration applications[J]. Automation of Electric Power Systems, 2015, 39(9): 26-33, 40. (  0) 0) |
| [6] |
李淋, 徐青山, 王晓晴, 等. 基于共享储能电站的工业用户日前优化经济调度[J]. 电力建设, 2020, 41(5): 100-107. LI Lin, XU Qingshan, WANG Xiaoqing, et al. Optimal economic scheduling of industrial customers on the basis of sharing energy-storage station[J]. Electric Power Construction, 2020, 41(5): 100-107. (  0) 0) |
| [7] |
YU D M, LIU H N, YAN G G, et al. Optimization of hybrid energy storage systems at the building level with combined heat and power generation[J]. Energies, 2017, 10(5): 606. DOI:10.3390/en10050606 (  0) 0) |
| [8] |
DI PIAZZA M C, LA TONA G, LUNA M, et al. A two-stage energy management system for smart buildings reducing the impact of demand uncertainty[J]. Energy and Buildings, 2017, 139: 1-9. DOI:10.1016/j.enbuild.2017.01.003 (  0) 0) |
| [9] |
MAVROMATIDIS G, OREHOUNIG K, CARMELIET J. Designing electrically self-sufficient distributed energy systems under energy demand and solar radiation uncertainty[J]. Energy Procedia, 2017, 122: 1027-1032. DOI:10.1016/j.egypro.2017.07.470 (  0) 0) |
| [10] |
SHABANPOUR-HAGHIGHI A, SEIFI A R. Effects of district heating networks on optimal energy flow of multi-carrier systems[J]. Renewable and Sustainable Energy Reviews, 2016, 59: 379-387. DOI:10.1016/j.rser.2015.12.349 (  0) 0) |
| [11] |
GU W, WANG J, LU S, et al. Optimal operation for integrated energy system considering thermal inertia of district heating network and buildings[J]. Applied Energy, 2017, 199: 234-246. DOI:10.1016/j.apenergy.2017.05.004 (  0) 0) |
| [12] |
XIE L, ILIC M D. Model predictive dispatch in electric energy systems with intermittent resources[C]//2008 IEEE International Conference on Systems, Man and Cybernetics. Singapore. IEEE: 42-47.
(  0) 0) |
| [13] |
吴成辉, 林声宏, 夏成军, 等. 基于模型预测控制的微电网群分布式优化调度[J]. 电网技术, 2020, 44(2): 530-538. WU Chenghui, LIN Shenghong, XIA Chengjun, et al. Distributed optimal dispatch of microgrid cluster based on model predictive control[J]. Power System Technology, 2020, 44(2): 530-538. (  0) 0) |
| [14] |
张彦, 张涛, 孟繁霖, 等. 基于模型预测控制的能源互联网系统分布式优化调度研究[J]. 中国电机工程学报, 2017, 37(23): 6829-6845, 7074. ZHANG Yan, ZHANG Tao, MENG Fanlin, et al. Model predictive control based distributed optimization and scheduling approach for the energy Internet[J]. Proceedings of the CSEE, 2017, 37(23): 6829-6845, 7074. (  0) 0) |
| [15] |
董雷, 陈卉, 蒲天骄, 等. 基于模型预测控制的主动配电网多时间尺度动态优化调度[J]. 中国电机工程学报, 2016, 36(17): 4609-4617. DONG Lei, CHEN Hui, PU Tianjiao, et al. Multi-time scale dynamic optimal dispatch in active distribution network based on model predictive control[J]. Proceedings of the CSEE, 2016, 36(17): 4609-4617. (  0) 0) |
| [16] |
杜祥伟, 沈艳霞, 李静. 基于模型预测控制的直流微网混合储能能量管理策略[J]. 电力系统保护与控制, 2020, 48(16): 69-75. DU Xiangwei, SHEN Yanxia, LI Jing. Energy management strategy of DC microgrid hybrid energy storage based on model predictive control[J]. Power System Protection and Control, 2020, 48(16): 69-75. (  0) 0) |
| [17] |
王成山, 洪博文, 郭力, 等. 冷热电联供微网优化调度通用建模方法[J]. 中国电机工程学报, 2013, 33(31): 26-33, 3. WANG Chengshan, HONG Bowen, GUO Li, et al. A general modeling method for optimal dispatch of combined cooling, heating and power microgrid[J]. Proceedings of the CSEE, 2013, 33(31): 26-33, 3. (  0) 0) |
| [18] |
BLOMMAERT M, WACK Y, BAELMANS M. An adjoint optimization approach for the topological design of large-scale district heating networks based on nonlinear models[J]. Applied Energy, 2020, 280: 116025. DOI:10.1016/j.apenergy.2020.116025 (  0) 0) |
| [19] |
GU W, WANG Z H, WU Z, et al. An online optimal dispatch schedule for CCHP microgrids based on model predictive control[J]. 2017 IEEE Power & Energy Society General Meeting, 2017, 1. (  0) 0) |
| [20] |
赵兵, 王增平, 纪维佳, 等. 基于注意力机制的CNN-GRU短期电力负荷预测方法[J]. 电网技术, 2019, 43(12): 4370-4376. ZHAO Bing, WANG Zengping, JI Weijia, et al. A short-term power load forecasting method based on attention mechanism of CNN-GRU[J]. Power System Technology, 2019, 43(12): 4370-4376. (  0) 0) |
2. School of Physical and Electronic Science, Chuxiong Normal University, Chuxiong 675000, China;
3. Yunnan Power Grid Co., Ltd. Research Institute, Kunming 650217, China

 骆钊(1986),男,博士,副教授,研究方向为区块链、电力市场、能源互联网、人工智能在电力系统中的应用(E-mail:
骆钊(1986),男,博士,副教授,研究方向为区块链、电力市场、能源互联网、人工智能在电力系统中的应用(E-mail: