文章编号: 2096-3203(2021)06-0165-08 中图分类号: TM732
2. 国网浙江省电力有限公司电力科学研究院, 浙江 杭州 310014
储能电站是利用大量储能元件进行电能储存、转换及释放的电站,由若干个不同或相同类型的储能系统组成[1]。其优化配置包括对储能电站容量、储能方式种类、运行功率和储能电站位置等进行优化[2-3],合理的优化配置能够平抑电网波动[4],参与市场调节[5],产生良好的经济效益和社会效益。
自然资源存在间歇性和波动性[6-7],系统在运行过程中,实际负荷数据和预测数据也存在差异,为应对调度不确定性,随机优化和鲁棒优化是现有的常用方法。随机优化通常基于概率分布函数的场景分析采样不确定性变量进行优化调度。文献[8]提出一种基于场景分析的含风电系统的优化运行组合模型;文献[9]提出一种根据节点注入的不确定性功率因素多阶段场景建模,随机规划的多阶段新型优化模型;文献[10]以改进的模糊规划系统为基础,构建一种模糊不确定性系统能源规划体系。以上文献所使用的计算方法都含有大量的概率统计,随机优化的计算时间随着场景的增大而迅速增加,而且获得准确的概率不确定性分布函数也很难,这些局限性阻碍了其广泛应用。鲁棒优化可以适当解决建立在基于集合不确定性之上的随机优化的这些限制,在优化调度中受到越来越多的关注。文献[11]提出一种新颖的两阶段“min-max-min”鲁棒优化孤岛优化调度,有效解决了AC/DC微电网协调稳定运行问题;文献[12]建立独立型微电网的双层鲁棒优化容量配置模型;文献[13]提出一种新颖的两阶段鲁棒优化方法,该方法可在考虑两阶段设置的预期性的同时,精确建模存储设备的非凸和时间耦合操作;文献[14-15]分别基于不同优化目标对储能系统的位置和容量进行优化。
鲁棒优化采用集合的方式来表征不确定量,旨在在最恶劣场景下保证电网稳定运行,是站在系统侧考虑的一种牺牲经济性的保守算法,忽略了决策者对于投资建设成本的预期目标。因此文中引入信息间隙决策理论(information gap decision theory, IGDT),IGDT能够在保证最终结果在不低于预期决策目标的情况下,最大化系统不确定参数的波动范围,可根据决策者的预期成本和考虑负荷长期增长的非随机不确定性,将经济性和鲁棒性、决策者对于风险的承受能力和投资建设预期目标结合起来[16-18],寻找最大限度应对增长不确定性和满足决策者预期目标的鲁棒性规划方案。文中搭建了基于IGDT的储能电站鲁棒优化配置模型,并以IEEE 33节点配电网系统为例对方案进行验证。
1 优化配置模型结构文中搭建基于IGDT的双层鲁棒优化配置模型,上层为规划层,旨在寻找决策预算目标下可承担最大波动性的储能电站配置方案;下层为运行层,搭建储能电站日前鲁棒优化运行模型,考虑运行约束,以日运行成本为优化运行目标,目的是评估上层决策方案的鲁棒性。二者相互影响,决策层应根据下层不确定性因素逐步观测,对上层进行调整。
1.1 IGDT鲁棒优化配置模型IGDT是一种含不确定参数的非概率的风险评估方法,不需要对历史数据进行大量采样获得复杂的概率模型,能够保证优化配置结果在小于可接受决策期望值的情况下最大化不确定因素的影响[18-19],将经济性和鲁棒性相结合,根据决策者的预算和需求选择合理的鲁棒性配置方案。当输入量为确定量时,典型模型可表示为:
| $ \begin{cases}\min F(x, p) & \\ \text { s.t. } \ \ \ \ G(x, p) \leqslant 0 \\ \ \ \ \ \ \ \ \ \ \ \ H(x, p)=0\end{cases} $ | (1) |
式中:F为决策目标;x为决策变量;p为输入参数;G(x, p),H(x, p)分别为不等式和等式约束。
文中F(x, p)为:
| $ F(x, p)=\min \left(C_{1}+C_{2}\right) $ | (2) |
| $ C_{1}=\sum\limits_{i=1}^{n}\left(C_{\mathrm{E}} E_{i}\right)+\sum\limits_{i=1}^{n}\left(C_{\mathrm{p}} P_{i}^{\max }\right) $ | (3) |
| $ C_{2}=\sum\limits_{t=1}^{T}\left(C_{\mathrm{in}}(t) P_{\mathrm{in}}(t)-C_{\mathrm{out}}(t) P_{\mathrm{out}}(t)\right) $ | (4) |
式中:C1为储能电站投资建设费用;C2为运行费用;CE为储能电站单位容量建设费用;Ei为储能电站i建设容量;Cp为储能电站单位运行功率建设费用;Pimax为储能电站i运行最大功率;n为投资建设储能电站个数;Cin(t),Cout(t)分别为t时刻配电网向大电网单位购电电价和单位售电电价;Pin(t),Pout(t)分别为t时刻配电网向大电网购电电量和售电电量;T为仿真运行周期。
风机光伏出力和用户负荷等输入参数p是不确定参数,参数在一定范围内波动,可表示为:
| $ p \in U(\alpha, \tilde{p}) $ | (5) |
| $ U(\alpha, \tilde{p})=\left\{p:\left|\frac{p-\tilde{p}}{p}\right| \leqslant \alpha\right\} $ | (6) |
式中:
当不确定参数p朝着对优化目标不利的方向变化时,可基于IGDT建立鲁棒性优化模型,鲁棒优化模型表示决策目标F(x, p)在低于可接受预算时,最大化不确定参数p的波动范围:
| $ \alpha\left(x, C_{\text {budget }}\right)=\max \left\{\alpha: F(x, p) \leqslant C_{\text {budget }}\right\} $ | (7) |
| $ C_{\text {budget }}= \begin{cases}(1+\delta) C_{0} & C_{0}>0, \delta>0 \\ (1-\delta) C_{0} & C_{0}<0, \delta>0\end{cases} $ | (8) |
式中:Cbudget为可接受预算;δ为预期成本偏差系数;C0为不考虑不确定性时预期投资值。
鲁棒性系数α值越大,表示可接受不确定参数p的波动程度越大,决策方案的鲁棒性越强;反之,α越小,表示对输入参数p的波动越敏感,系统的鲁棒性也随之减弱。文中可将IGDT一般模型转化为IGDT鲁棒优化模型:
| $ \left\{\begin{array}{l} \max \left(\alpha_{\mathrm{w}}, \alpha_{\mathrm{pv}}, \alpha_{1}\right) \\ \text { s.t. } \quad \min \left(C_{1}+C_{2}\right) \leqslant C_{\text {budget }} \\ \quad \quad \quad p \in U(\alpha, \tilde{p}) \\ \quad \quad \quad G(\alpha, \tilde{p}) \leqslant 0 \\ \quad \quad \quad H(\alpha, \tilde{p})=0 \end{array}\right. $ | (9) |
式中:αw,αpv,αl分别为风机、光伏和负荷的最大波动性。
1.2 上层优化配置模型为提高规划方案应对工程期内系统负荷长期增长的鲁棒性,同时考虑风机、光伏2个不确定参数,所以目标函数为系统内不确定因素的最大波动性。在使用最优求解算法时,αw,αpv,αl之间存在矛盾,即其中一项参数的增长会导致另外两项参数的减少。如投资建设预期目标一定,最大化系统所能承受的负荷波动,计算得到的系统所能承受风机与光伏波动性结果就会减少。因此,优化配置模型为多目标优化配置模型,目标函数如下:
| $ f=\max \left(\alpha_{\mathrm{w}}, \alpha_{\mathrm{pv}}, \alpha_{1}\right) $ | (10) |
多目标优化配置比单目标更加复杂,多个目标之间存在冲突,为综合考虑3种因素的不确定性给系统带来的冲突,对优化目标中的变量根据重要程度进行线性加权,将多目标问题转化为单目标问题:
| $ \left\{\begin{array}{l} f=\lambda_{1} \alpha_{\mathrm{w}}+\lambda_{2} \alpha_{\mathrm{pv}}+\lambda_{3} \alpha_{1} \\ \text { s.t. } \quad \min \left(C_{1}+C_{2}\right) \leqslant C_{\text {budget }} \end{array}\right. $ | (11) |
式中:λ1,λ2,λ3为权重系数。
1.3 下层鲁棒优化运行模型文中以最大化储能电站所在配电网系统的经济性为主要目标进行日前运行优化,即目标函数为配电网购电费用最小:
| $ \begin{array}{c} \min f = \\ \min \mathop {\max }\limits_\alpha \sum\limits_{i = 1}^T {\left( {{C_{{\rm{in }}}}(t){P_{{\rm{in }}}}(t) - {C_{{\rm{out }}}}(t){P_{{\rm{out }}}}(t)} \right)} \end{array} $ | (12) |
由于储能电站服务于配电网运行,因此储能电站在运行中会受到配电网内不确定因素波动范围α的影响,鲁棒优化即在最大不确定因素的情况下通过变量作用尽可能最小化优化目标。文中系统运行优化目标即为日运行费用:
| $ \left\{\begin{aligned} &\min _{y} \max _{\alpha}\left(\boldsymbol{d}^{\mathrm{T}} \boldsymbol{Y}\right) \\ &\text { s.t. }\ \ \ \ G(x, y) \leqslant 0 \\ & \ \ \ \ \ \ \ \ \ \ \ \ H(x, y)=0 \\ & \ \ \ \ \ \ \ \ \ \ \ \ \alpha \in U \end{aligned}\right. $ | (13) |
式中:dT为求解目标函数中y变量系数形成的行向量;x为决策变量,即储能电站建设容量与额定充放电功率决策变量;y为连续型变量,包含支路潮流变量、节点电压变量、负荷变量、风机与光伏出力变量;Y为y变量集合形成的列向量;G(x, y)≤0,H(x, y)=0分别为运行不等式和等式约束。
| $ \boldsymbol{X}=[\text { 容量 } 1, \cdots \text {, 容量 } n \text {, 功率 } 1, \cdots \text {, 功率 } n]^{\mathrm{T}} $ | (14) |
| $ \boldsymbol{Y}=\left[Y_{1-1}, Y_{1-2}, Y_{1-3}, Y_{1-4}, Y_{2}, Y_{3-1}, Y_{3-2}, Y_{3-3}, Y_{4}, Y_{5}\right]^{\mathrm{T}} $ | (15) |
式中:X为x变量集合形成的列向量;以从线路始端到线路末端潮流方向为正向,反之为负向,Y1-1为支路正向有功变量集合,每条线路每天共24个状态;Y1-2为支路负向有功变量集合;Y1-3为支路正向无功变量集合;Y1-4为支路负向无功变量集合;Y2为节点电压变量集合;Y3-1为储能充电变量集合;Y3-2为储能放电变量集合;Y3-3为储能荷电状态变量集合;Y4为风机出力变量集合;Y5为光伏出力变量集合。
1.4 下层运行约束(1) 分布式电源出力约束。即:
| $ 0 \leqslant P_{\text {wind }}(t) \leqslant P_{\text {wind }}^{\max } $ | (16) |
| $ 0 \leqslant P_{\mathrm{pv}}(t) \leqslant P_{\mathrm{pv}}^{\max } $ | (17) |
式中:Pwindmax,Ppvmax分别为风机和光伏最大容量;Pwind(t),Ppv(t)分别为风机和光伏在t时刻出力。
(2) 储能电站运行约束。在均衡电路的作用下,各电池串荷电状态(state of charge, SOC)变化保持一致,所以电池组的输出特性与电池串的输出特性保持一致,即可认为与电池单体输出特性保持一致,电池组可以简化为戴维宁等效模型进行计算仿真处理。假设在仿真步长内,储能电站与电网之间的交流功率为恒定值,则模型可以简化为:
| $ \begin{gathered} S(t+\Delta t)=S(t)(1-\sigma)+ \\ \eta_{\mathrm{c}} P_{\mathrm{ch}}(t) \Delta t-P_{\mathrm{dis}}(t) \Delta t / \eta_{\mathrm{d}} \end{gathered} $ | (18) |
式中:S为电池电量;σ为自放电率;ηc为功率转换系统整流转换效率;Pch为储能电站吸收电功率;Δt为仿真步长;Pdis为储能电站释放电功率;ηd为功率转换系统逆变转换效率。
储能电站其他运行约束:
| $ \left\{\begin{array}{l} E_{\mathrm{bat}, \mathrm{min}} \leqslant E_{\mathrm{bat}}(t) \leqslant E_{\mathrm{bat}, \max } \\ F_{\mathrm{c}}(t)+F_{\mathrm{d}}(t) \leqslant 1 \\ F_{\mathrm{c}}(t), F_{\mathrm{d}}(t) \in\{0,1\} \\ 0 \leqslant P_{\mathrm{ch}}(t) \leqslant F_{\mathrm{c}}(t) P_{\mathrm{c}}^{\max } \\ 0 \leqslant P_{\mathrm{dis}}(t) \leqslant F_{\mathrm{d}}(t) P_{\mathrm{dis}}^{\max } \\ E_{\mathrm{bat}}(1)=E_{\mathrm{bat}}\left(T_{\mathrm{s}}+1\right) \end{array}\right. $ | (19) |
式中:Ebat(t)为t时刻电池电量;Ebat, max,Ebat, min分别电池电量上、下限;Fc,Fd分别为充、放电标志位;Pch,Pdis分别为储能电站充、放电功率;Pcmax,Pdismax分别为充、放电功率上限;Ts为运行周期。
(3) 潮流约束。潮流电压约束为:
| $ P_{i+1}(t)=P_{i}(t)-P_{i, \mathrm{~L}}(t)+P_{i, \mathrm{G}}(t) $ | (20) |
| $ Q_{i+1}(t)=Q_{i}(t)-Q_{i, \mathrm{~L}}(t) $ | (21) |
节点电压方程为:
| $ V_{i+1}(t)=V_{i}(t)-\frac{r_{i} P_{i}(t)+x_{i} Q_{i}(t)}{V_{0}} $ | (22) |
电压应该限制在合理范围以内:
| $ V_{\min } \leqslant V_{i}(t) \leqslant V_{\max } $ | (23) |
式中:Pi,Qi分别为节点i-1流向节点i的有功功率和无功功率;Pi, L,Qi, L分别为节点i有功负荷和无功负荷;Pi, G为节点i分布式电源与储能出力总和;ri,xi分别为节点i-1与节点i之间的电阻值与电抗值;Vi为节点i电压幅值;V0为系统电压基准值;Vmax,Vmin分别为节点电压上、下限。
潮流容量约束:
| $ 0 \leqslant P_{i}(t) \leqslant P_{i, \text { lim }} $ | (24) |
| $ 0 \leqslant Q_{i}(t) \leqslant Q_{i, \text { lim }} $ | (25) |
式中:Pi, lim,Qi, lim分别节点i-1流向节点i的有功功率和无功功率上限。
2 广义Benders分解法文中使用广义Benders分解法对上述优化模型进行求解,将原问题划分为主问题和子问题[12, 17, 19]。主问题即决策层为储能电站初次投资建设问题,即要决定储能电站的建设容量与运行功率;子问题即运行问题,在考虑风、光等自然资源和负荷不确定集的情况下最小化运行成本。
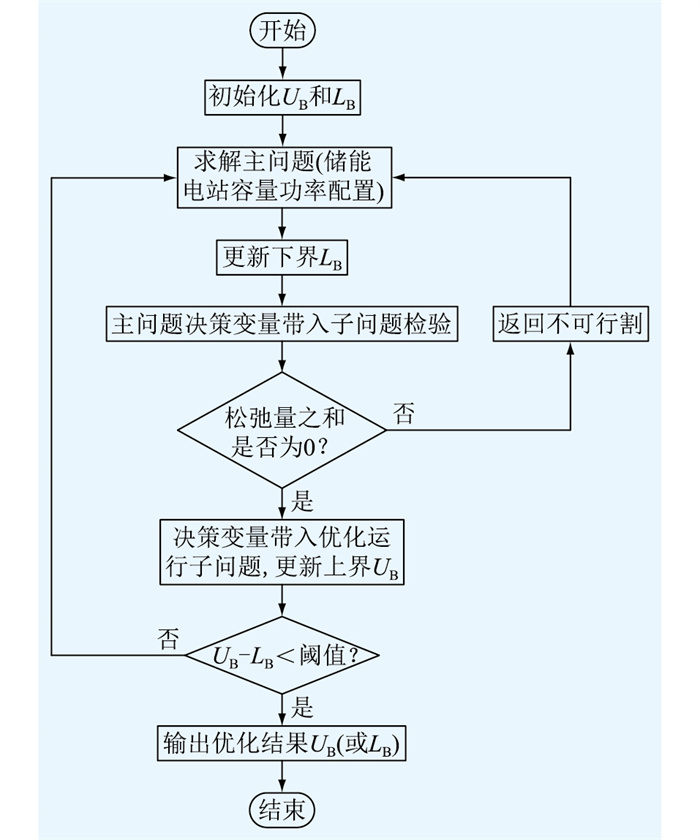
2.1 分解流程分解流程如图 1所示,具体步骤如下。
|
图 1 广义Benders分解法流程 Fig. 1 Generalized Benders decomposition method flow chart |
(1) 初始化主问题决策变量,即储能电站容量与运行功率,原问题上界UB和下界LB。
(2) 求解储能电站容量与功率主问题,更新原问题下界LB。
(3) 将主问题中所求得的储能电站建设容量与运行功率带入可行性子问题进行检验,判断决策变量是否能够满足子问题所有运行约束条件。若可行性检验子问题中的所有松弛变量(文中为节点电压松弛量)之和可实现为零,则说明问题可行,转步骤(4);反之,则说明主问题决策变量不满足约束条件,返回不可行割,转步骤(2),主问题重新对决策变量求解调整。
(4) 主问题决策变量满足所有约束、将决策变量带入运行优化子问题,通过对偶进行求解,更新原问题上界UB。
(5) 若UB-LB的值小于设置检验偏差,则说明原问题已达到最优解,跳出循环;否则返回主问题可行割,转步骤(2),直至寻找到最优解。
2.2 问题划分(1) 经济最优运行子问题。经济运行最优子问题是在不确定因素作用使目标函数值日运行成本变大的情况下,在调整变量作用下使日运行成本尽可能小,具体如下:
| $ \begin{gathered} \varphi^{(\omega)}=\min \max \limits_{\alpha} C_{2}= \\ \min \max \limits_{\alpha} \sum\limits_{t=1}^{T}\left(C_{\mathrm{in}}(t) P_{\mathrm{in}}(t)-C_{\mathrm{out}}(t) P_{\mathrm{out}}(t)\right)= \\ \max \limits_{y} \max \limits_{\alpha}\left(\boldsymbol{d}^{\mathrm{T}} \boldsymbol{Y}\right) \end{gathered} $ | (26) |
将约束条件矩阵化:
| $ {\mathit{\boldsymbol{DY}} \le \mathit{\boldsymbol{f}}} $ | (27) |
| $ {\mathit{\boldsymbol{EY}} = \mathit{\boldsymbol{g}}} $ | (28) |
| $ {\mathit{\boldsymbol{FY}} \le \mathit{\boldsymbol{h}} - \mathit{\boldsymbol{GX}}} $ | (29) |
| $ {\mathit{\boldsymbol{JY}} = \mathit{\boldsymbol{w}}} $ | (30) |
| $ {\mathit{\boldsymbol{KY}} = {\mathit{\boldsymbol{p}}_{{\rm{pv}}}}} $ | (31) |
| $ {\mathit{\boldsymbol{MY}} = \mathit{\boldsymbol{l}}} $ | (32) |
式(27)为式(20)—式(25)约束矩阵化;式(28)为式(18)约束矩阵化;式(29)为式(19)约束矩阵化;式(30)为风机出力预测;式(31)为光伏出力预测;式(32)为电功率平衡约束;ω为迭代次数;D,E,F,J,K,M均由变量约束系数组成,将Y中所对应的变量进行提取与计算,其列数与Y相同;f,g,h,G,w,ppv,l为由约束上限与下限所组成的列向量。
采用拉格朗日对偶法对求解问题进行对偶,转化成最大值求解问题:
| $ \left\{\begin{array}{l} \max \left[-\boldsymbol{\rho}^{\mathrm{T}} \boldsymbol{f}+\boldsymbol{\beta}_{1}^{\mathrm{T}} \boldsymbol{g}-\boldsymbol{\beta}_{2}^{\mathrm{T}} \boldsymbol{g}-\boldsymbol{\chi}^{\mathrm{T}}(\boldsymbol{h}-\boldsymbol{G} \boldsymbol{x})+\right. \\ \left.\quad \boldsymbol{\gamma}_{1}^{\mathrm{T}} \boldsymbol{w}-\boldsymbol{\gamma}_{2}^{\mathrm{T}} \boldsymbol{w}+\boldsymbol{\psi}_{1}^{\mathrm{T}} \boldsymbol{p}_{\mathrm{pv}}-\boldsymbol{\psi}_{2}^{\mathrm{T}} \boldsymbol{p}_{\mathrm{pv}}+\boldsymbol{u}_{1}^{\mathrm{T}} \boldsymbol{l}-\boldsymbol{u}_{2}^{\mathrm{T}} \boldsymbol{l}\right] \\ \text { s.t. }\quad-\boldsymbol{\rho}^{\mathrm{T}} \boldsymbol{D}+\boldsymbol{\beta}_{1}^{\mathrm{T}} \boldsymbol{E}-\boldsymbol{\beta}_{2}^{\mathrm{T}} \boldsymbol{E}-\boldsymbol{\chi}^{\mathrm{T}} \boldsymbol{F}+\boldsymbol{\gamma}_{1}^{\mathrm{T}} \boldsymbol{J}- \\ \quad\quad\quad\boldsymbol{\gamma}_{2}^{\mathrm{T}} \boldsymbol{J}+\boldsymbol{\psi}_{1}^{\mathrm{T}} \boldsymbol{K}-\boldsymbol{\psi}_{2}^{\mathrm{T}} \boldsymbol{K}+\boldsymbol{u}_{1}^{\mathrm{T}} \boldsymbol{M}-\boldsymbol{u}_{2}^{\mathrm{T}} \boldsymbol{M}=\boldsymbol{d}^{\mathrm{T}} \\ \quad\quad\quad\boldsymbol{\rho} \geqslant 0, \boldsymbol{\chi} \geqslant 0, \boldsymbol{\gamma} \geqslant 0, \boldsymbol{\psi} \geqslant 0 \end{array}\right. $ | (33) |
式中:ρ,β,χ,γ,ψ,u为Y的对偶变量。
(2) 可行性子问题。可行性子问题的约束条件相比于经济最优运行子问题的某些约束条件多了松弛变量。文中将松弛变量添加到电压约束中,优化目标如下。
节点电压松弛变量:
| $ V_{\min }-S_{1} \leqslant V_{i}(t) \leqslant V_{\max }+S_{2} \quad S_{1} \geqslant 0, S_{2} \geqslant 0 $ | (34) |
优化目标:
| $ \varphi^{(\omega)}=\min \max S=S_{1}+S_{2} $ | (35) |
(3) 主问题。当松弛变量之和为0时,即电网节点电压都在合理范围内时,证明规划层方案可以实现系统稳定运行,转向优化运行子问题,否则返回给主问题不可行割:
| $ \begin{gathered} \varphi^{(\omega)}-\boldsymbol{\chi}^{\mathrm{T}}\left(\boldsymbol{h}-\boldsymbol{G}\left(x-x_{i}^{\omega-1}\right)\right)+ \\ \boldsymbol{\gamma}_{1}^{\mathrm{T}} \boldsymbol{\omega}\left(\alpha_{\mathrm{w}}-\alpha_{\mathrm{w}, i}^{\omega-1}\right)-\boldsymbol{\gamma}_{2}^{\mathrm{T}} \boldsymbol{\omega}\left(\alpha_{\mathrm{w}}-\alpha_{\mathrm{w}, i}^{\omega-1}\right)+ \\ \boldsymbol{\psi}_{1}^{\mathrm{T}} \boldsymbol{p} \boldsymbol{v}\left(\alpha_{\mathrm{pv}}-\alpha_{\mathrm{pv}, i}^{\omega-1}\right)-\boldsymbol{\psi}_{2}^{\mathrm{T}} \boldsymbol{p}_{\mathrm{pv}}\left(\alpha_{\mathrm{pv}}-\alpha_{\mathrm{pv}, i}^{\omega-1}\right)+ \\ \boldsymbol{u}_{1}^{\mathrm{T}} \boldsymbol{l}\left(\alpha_{1}-\alpha_{1, i}^{\omega-1}\right)-\boldsymbol{u}_{2}^{\mathrm{T}} \boldsymbol{l}\left(\alpha_{1}-\alpha_{1, i}^{\omega-1}\right) \leqslant 0 \end{gathered} $ | (36) |
若子问题可行,最优运行子问题给主问题增加的可行割为:
| $ \begin{gathered} Z \geqslant \varphi^{(\omega)}-\boldsymbol{\chi}^{\mathrm{T}}\left(\boldsymbol{h}-\boldsymbol{G}\left(x-x_{i}^{\omega-1}\right)\right)+ \\ \boldsymbol{\gamma}_{1}^{\mathrm{T}} \boldsymbol{\omega}\left(\alpha_{\mathrm{w}}-\alpha_{\mathrm{w}, i}^{\omega-1}\right)-\boldsymbol{\gamma}_{2}^{\mathrm{T}} \boldsymbol{\omega}\left(\alpha_{\mathrm{w}}-\alpha_{\mathrm{w}, i}^{\omega-1}\right)+ \\ \boldsymbol{\psi}_{1}^{\mathrm{T}} \boldsymbol{p} \boldsymbol{v}\left(\alpha_{\mathrm{pv}}-\alpha_{\mathrm{pv}, i}^{\omega-1}\right)-\boldsymbol{\psi}_{2}^{\mathrm{T}} \boldsymbol{p}_{\mathrm{pv}}\left(\alpha_{\mathrm{pv}}-\alpha_{\mathrm{pv}, i}^{\omega-1}\right)+ \\ \boldsymbol{u}_{1}^{\mathrm{T}} \boldsymbol{l}\left(\alpha_{1}-\alpha_{1, i}^{\omega-1}\right)-\boldsymbol{u}_{2}^{\mathrm{T}} \boldsymbol{l}\left(\alpha_{1}-\alpha_{1, i}^{\omega-1}\right) \end{gathered} $ | (37) |
规划层以最大化不确定因素波动为优化目标,主问题数学模型如式(38)所示。
| $ \begin{cases}\max \left(\lambda_{1} \alpha_{\mathrm{w}}+\lambda_{2} \alpha_{\mathrm{pv}}+\lambda_{3} \alpha_{1}\right) & \\ \text { s.t. }\ \ \ \ \text { 式(36), 式(37) } \\\ \ \ \ \ \ \ \ \ \ \ \ \boldsymbol{X} \geqslant 0\end{cases} $ | (38) |
原问题下界:
| $ L_{\mathrm{B}}=\lambda_{1} \alpha_{\mathrm{w}}+\lambda_{2} \alpha_{\mathrm{pv}}+\lambda_{3} \alpha_{1}+Z $ | (39) |
式中:Z为运行优化子问题的目标函数值。
原问题上界:
| $ U_{\mathrm{B}}=\varphi^{(\omega)}+\max \left(\lambda_{1} \alpha_{\mathrm{w}}+\lambda_{2} \alpha_{\mathrm{pv}}+\lambda_{3} \alpha_{1}\right) $ | (40) |
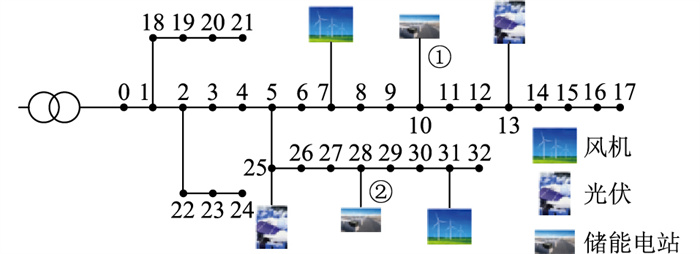
采用IEEE 33节点辐射配电网络系统,具体如图 2所示。
|
图 2 系统网络 Fig. 2 System network |
电源网络首端基准电压为12.66 kV,每个节点的电压范围为0.95~1.05 p.u.。节点7和节点31接有风机;节点13和节点25接有光伏;节点10和节点28分别为储能电站①和②安装位置,储能电站充、放电效率均为0.9,运行过程中的电量上限为额定容量,运行下限为额定容量的30%,额定运行功率为安装容量的1/2,工程寿命周期10 a。调用YALMIP工具箱与Gurobi求解器进行求解。
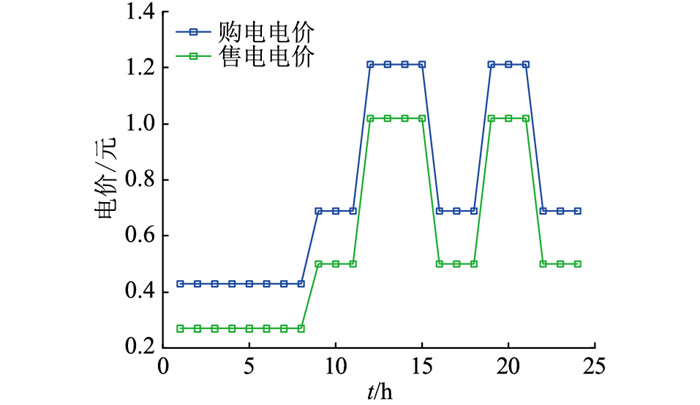
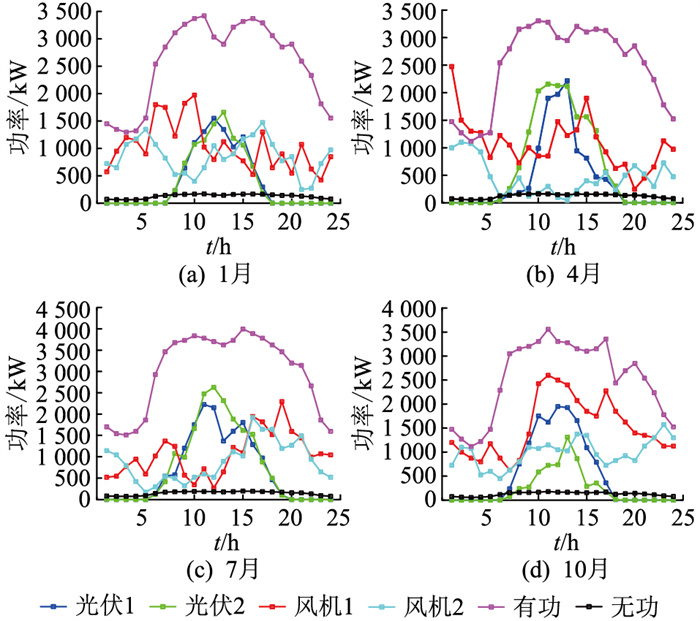
使用一年8 760 h进行优化,计算量庞大,为简化计算,同时涵盖四季特点,在进行优化配置时,选择四季典型日进行计算。图 3为24 h电网电价[21];图 4为四季典型日在确定情况下,分布式电源出力和负荷情况。
|
图 3 电网电价 Fig. 3 Grid electricity price |
|
图 4 典型四季负荷和分布式电源出力 Fig. 4 Typical load and distributed power supply output in four seasons |
储能电站的主要储能设备为磷酸铁锂电池,单位容量成本为2 000元/(kW ·h),单位功率成本为1 500元/kW,每年的运行维护费用占投资成本的1%。单独考虑系统αw,αpv和αl与δ关系时,三者数值差异较小,故在文中算例中,令三者相等,取λ1=λ2=λ3=1/3。
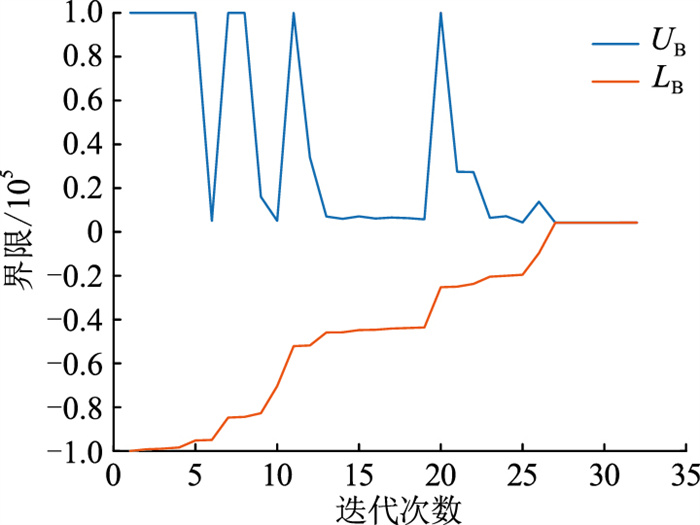
3.2 结果分析图 5为使用Benders分解法对δ=0时进行求解的收敛过程,共迭代33次,收敛于5 761.5。
|
图 5 广义Benders分解法收敛过程 Fig. 5 Convergence process of generalized Benders decomposition method |
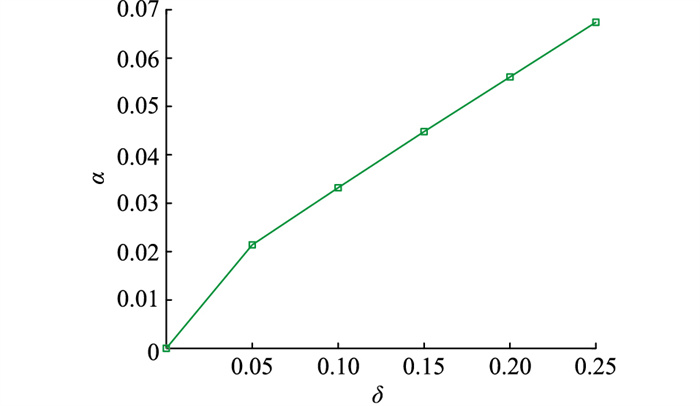
表 1为不同预期偏差系数下储能电站优化配置结果,图 6为鲁棒性系数α与预期偏差系数δ关系曲线。
|
|
表 1 配置结果 Table 1 Results of configuration |
|
图 6 鲁棒性系数α与预期偏差系数δ关系 Fig. 6 Relationship between robustness coefficient α and expected deviation coefficient δ |
由表 1可知,在不考虑不确定因素波动时,预期成本为每日5 761.5元,即每日配电网系统预期支出C0为5 761.5元。由图 6可以看出,随着预期偏差系数δ的逐渐增大,决策者可接受的系统收益逐渐降低,系统鲁棒性系数α也在逐渐增大,系统所允许的不确定因素最大波动范围也在逐渐增大,所能够接受的运行场景也就越恶劣。决策者可根据负荷预见增长趋势和自身状况决定所要建设系统的鲁棒性。
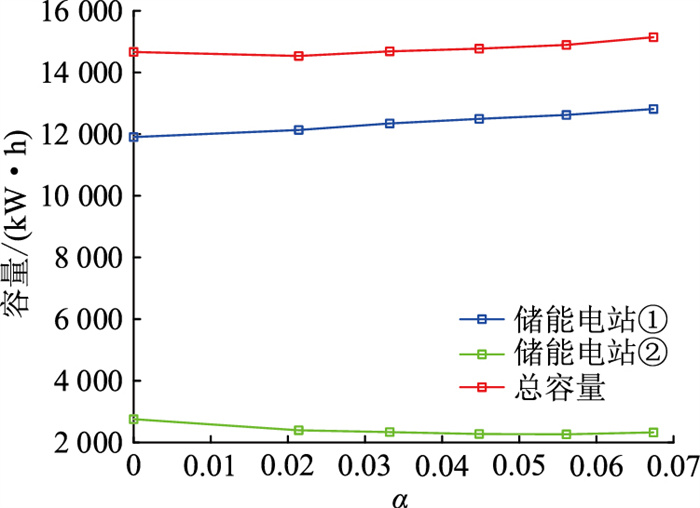
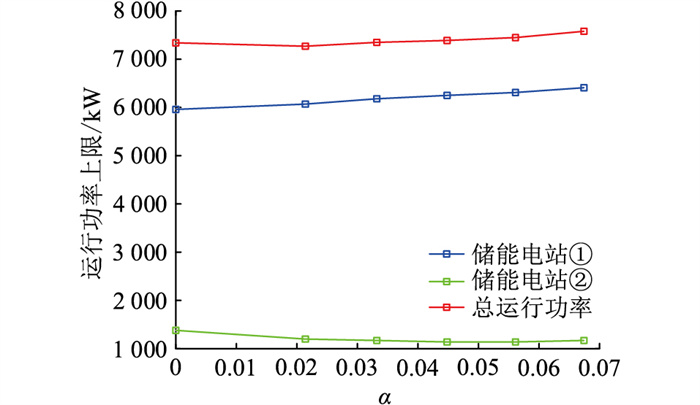
图 7和图 8分别为鲁棒性系数与储能电站容量关系曲线和鲁棒性系数与储能电站额定运行功率关系曲线。图 7和图 8表明,随着预期目标增加,鲁棒系数的增大,储能电站①容量和运行功率逐渐上升,储能电站②容量与额定运行功率首先呈下降趋势,在δ=25%时略有上升。在恶劣场景下,随着系统内的不确定因素波动幅度增加,系统倾向于增加内部可控因素占比来增强系统的鲁棒性,故系统内可用储能电站的容量与额定运行功率之和总体上大致呈上升趋势。
|
图 7 鲁棒性系数与储能电站容量关系 Fig. 7 Relationship between robustness coefficient and capacity of energy storage power station |
|
图 8 鲁棒性系数与储能电站额定运行功率关系 Fig. 8 Relationship between robustness coefficient and rated operating power of energy storage power station |
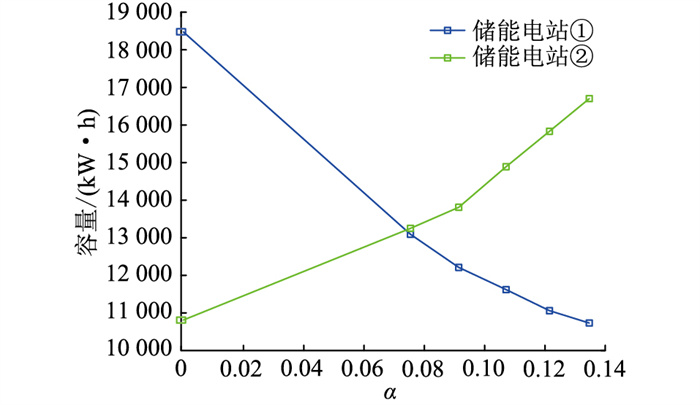
当储能换成成本较低的铅酸电池后(单位容量成本为800元/(kW ·h),单位功率成本为1 500元/kW),其容量优化配置结果如图 9所示。与图 7相比,储能电站②容量上升明显,储能电站①容量却有所下降。储能电站②与配电网功率联络线距离较近,从本例角度来说,功率联络线传输功率属于可控量,因此,可由储能电站与功率联络线共同承担系统波动,由算法来判断承担出力。当储能成本明显降低时,储能电站②更接近大电网系统,倾向于容量变大,从大电网中转移更多电能满足负荷需求,储能电站①则容量有所下降,系统从大电网中购电增加,成本上升,系统内可控变量增加,鲁棒性上升。当储能的成本较高时,由于经济性因素的限制,储能电站低储高发套利运行倾向减少,储能电站①和②容量随着鲁棒性系数的增强,在经济允许范围内,有所增长。
|
图 9 鲁棒性系数与铅酸电池储能电站容量关系 Fig. 9 Relationship between robustness coefficient and lead-acid battery energy storage power station capacity |
文中以储能电站出力数学模型和运行优化模型为基础提出了基于IGDT的储能电站鲁棒优化配置方法。基于电网系统的运行情况、负荷情况,搭建优化配置模型,在优化配置模型的建立过程中,基于IGDT提高系统经济性,以鲁棒模型应对可再生能源和负荷的波动,得到结合系统经济性与鲁棒性的优化配置方案。文中所提模型与传统鲁棒优化配置模型不同,更多的是从工程投资角度出发,以决策者所能承受的最大投资期望值来计算储能电站的鲁棒性,考虑了决策者的经济承担能力,将鲁棒性与经济性相结合,在可接受预期目标下寻找最优方案,为储能电站及电网系统建设提供参考。
| [1] |
曹飞. 储能电站: 电网的"充电宝"[J]. 大众用电, 2018, 32(8): 18. CAO Fei. Energy storage power station: the 'power bank' of the power grid[J]. Popular Utilization of Electricity, 2018, 32(8): 18. (  0) 0) |
| [2] |
李湘旗, 禹海峰, 李欣然, 等. 考虑储能系统动态全寿命周期特性的多功能应用需求规划方法[J]. 电力建设, 2020, 41(1): 45-54. LI Xiangqi, YU Haifeng, LI Xinran, et al. Planning method for multi-functional application demand considering dynamic life cycle characteristics of energy storage[J]. Electric Power Construction, 2020, 41(1): 45-54. (  0) 0) |
| [3] |
聂聪颖, 沈小军, 吕洪, 等. 并网型风电场氢超混合储能容量配置及控制策略研究[J]. 智慧电力, 2020, 48(9): 1-8. NIE Congying, SHEN Xiaojun, LYU Hong, et al. Capacity configuration and control strategy of hydrogen super hybrid energy storage in grid connected wind farm[J]. Smart Power, 2020, 48(9): 1-8. (  0) 0) |
| [4] |
梁剑, 余虎, 杨高才, 等. 电池储能技术在风电系统调峰优化中的应用[J]. 电力信息与通信技术, 2020, 18(10): 67-73. LIANG Jian, YU Hu, YANG Gaocai, et al. Application of battery energy storage technology in peak regulation optimization of wind power system[J]. Electric Power Information and Communication Technology, 2020, 18(10): 67-73. (  0) 0) |
| [5] |
谢敏, 韦薇, 李建钊, 等. 储能电站参与能量-调频市场联合调度模式研究[J]. 电力建设, 2019, 40(2): 20-28. XIE Min, WEI Wei, LI Jianzhao, et al. Research on combined dispatching mode of energy storage in energy market and regulation market[J]. Electric Power Construction, 2019, 40(2): 20-28. DOI:10.3969/j.issn.1000-7229.2019.02.003 (  0) 0) |
| [6] |
郭扬, 李金叶. 我国新能源对化石能源的替代效应研究[J]. 可再生能源, 2018, 36(5): 762-770. GUO Yang, LI Jinye. The substitution effect on new energy research and fossil energy in China[J]. Renewable Energy Resources, 2018, 36(5): 762-770. DOI:10.3969/j.issn.1671-5292.2018.05.022 (  0) 0) |
| [7] |
刘福盛, 张兰, 卢学佳, 等. 基于信度网络推理的风电监控数据缺失值恢复算法[J]. 电力信息与通信技术, 2019, 17(4): 48-55. LIU Fusheng, ZHANG Lan, LU Xuejia, et al. Wind power monitoring data missing value recovery algorithm based on belief network[J]. Electric Power Information and Communication Technology, 2019, 17(4): 48-55. (  0) 0) |
| [8] |
雷宇. 基于场景分析的含风电场电力系统机组组合问题的研究[D]. 济南: 山东大学, 2013. LEI Yu. Studies on unit commitment considering wind power based on scenario analysis in power systems[D]. Jinan: Shandong University, 2013. (  0) 0) |
| [9] |
龙军, 莫群芳, 曾建. 基于随机规划的含风电场的电力系统节能优化调度策略[J]. 电网技术, 2011, 35(9): 133-138. LONG Jun, MO Qunfang, ZENG Jian. A stochastic programming based short-term optimization scheduling strategy considering energy conservation for power system containing wind farms[J]. Power System Technology, 2011, 35(9): 133-138. (  0) 0) |
| [10] |
胡情. 模糊不确定性优化理论在能源规划中的应用[D]. 北京: 华北电力大学, 2013. HU Qing. Inexact fuzzy optimization theory and its application in energy systems planning[D]. Beijing: North China Electric Power University, 2013. (  0) 0) |
| [11] |
ZHAO B, QIU H F, QIN R W, et al. Robust optimal dispatch of AC/DC hybrid microgrids considering generation and load uncertainties and energy storage loss[J]. IEEE Transactions on Power Systems, 2018, 33(6): 5945-5957. DOI:10.1109/TPWRS.2018.2835464 (  0) 0) |
| [12] |
刘思夷, 赵波, 汪湘晋, 等. 基于Benders分解的独立型微电网鲁棒优化容量配置模型[J]. 电力系统自动化, 2017, 41(21): 119-126, 146. LIU Siyi, ZHAO Bo, WANG Xiangjin, et al. Capacity configuration model for robust optimization of stand-alone microgrid based on Benders decomposition[J]. Automation of Electric Power Systems, 2017, 41(21): 119-126, 146. DOI:10.7500/AEPS20161228012 (  0) 0) |
| [13] |
COBOS N G, ARROYO J M, ALGUACIL N, et al. Robust energy and reserve scheduling considering bulk energy storage units and wind uncertainty[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5206-5216. DOI:10.1109/TPWRS.2018.2792140 (  0) 0) |
| [14] |
AWAD A S A, EL-FOULY T H M, SALAMA M M A. Optimal ESS allocation and load shedding for improving distribution system reliability[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2339-2349. DOI:10.1109/TSG.2014.2316197 (  0) 0) |
| [15] |
李秀磊, 耿光飞, 季玉琦, 等. 考虑实际运行的配电网电池储能系统的优化配置研究[J]. 电力系统保护与控制, 2017, 45(9): 88-94. LI Xiulei, GENG Guangfei, JI Yuqi, et al. Study on optimal allocation of battery energy storage in distribution network considering the actual operation[J]. Power System Protection and Control, 2017, 45(9): 88-94. (  0) 0) |
| [16] |
马欢, 刘玉田. 基于IGDT鲁棒模型的风电爬坡事件协调调度决策[J]. 中国电机工程学报, 2016, 36(17): 4580-4589. MA Huan, LIU Yutian. IGDT robust model-based coordinated scheduling strategy for wind power ramp events[J]. Proceedings of the CSEE, 2016, 36(17): 4580-4589. (  0) 0) |
| [17] |
ALEMANY J M, MAGNAGO F, MOITRE D. Benders decomposition applied to security constrained unit commitment[J]. IEEE Latin America Transactions, 2013, 11(1): 421-425. DOI:10.1109/TLA.2013.6502840 (  0) 0) |
| [18] |
张皓, 荆朝霞. 基于IGDT模型的海岛型微网容量鲁棒优化[J]. 自动化与仪器仪表, 2017(7): 59-62. ZHANG Hao, JING Zhaoxia. Optimization for capacity configuration of island microgrid based on IGDT[J]. Automation & Instrumentation, 2017(7): 59-62. (  0) 0) |
| [19] |
MIRZAEI M A, NAZARI-HERIS M, MOHAMMADI-IVATLOO B, et al. Network-constrained joint energy and flexible ramping reserve market clearing of power- and heat-based energy systems: a two-stage hybrid IGDT-stochastic framework[J]. IEEE Systems Journal, 2021, 15(2): 1547-1556. DOI:10.1109/JSYST.2020.2996952 (  0) 0) |
| [20] |
TASKI N, CANER Z. Benders decomposition[M]//Wiley Encyclopedia of Operations Research and Management Science. 2010.
(  0) 0) |
| [21] |
陈健, 张维桐, 张逸成, 等. 考虑不同空调负荷特性的微网双层优化调度[J]. 电网技术, 2018, 42(5): 1424-1431. CHEN Jian, ZHANG Weitong, ZHANG Yicheng, et al. Bi-level optimal dispatch of microgrid considering different air-conditioning load characteristics[J]. Power System Technology, 2018, 42(5): 1424-1431. (  0) 0) |
2. State Grid Zhejiang Electric Power Co., Ltd. Research Institute, Hangzhou 310014, China

 潘乐真(1984), 女, 硕士, 高级工程师, 从事电网规划、新能源管理工作(E-mail:
潘乐真(1984), 女, 硕士, 高级工程师, 从事电网规划、新能源管理工作(E-mail: