2. 复旦大学附属中山医院厦门分院中西医结合科,厦门 361000
2. Department of Integrative Chinese and Western Medicine, Xiamen Branch of Zhongshan Hospital, Fudan University, Xiamen 361000, Fujian, China
乳腺癌已成为危害女性健康的重大疾病之一。据2020年全球癌症统计数据显示,乳腺癌的发病率跃居全球首位,新发病例数高达226万例,其中中国女性新发乳腺癌病例近42万例[1]。浸润性乳腺癌是最常见的乳腺癌病理分型,恶性程度高,预后较差。我国女性乳腺癌中,70%以上为浸润性导管癌,其他组织类型,如浸润性导管和小叶癌、浸润性小叶癌及浸润性小叶癌合并其他型癌等,均未超过5%[2]。当前国内外浸润性乳腺癌的预后研究较为广泛,但存在数据量不足、方法单一、忽略不平衡性等问题[3-4]。为了更好地辅助临床医师判断治疗效果及患者预后情况,有必要建立一个样本量大、统计效能高、方法严谨的浸润性乳腺癌患者的预后模型。
美国国立癌症研究所监测、流行病学和终点事件(Surveillance,Epidemiology,and End Results;SEER)是全球最具代表性的大型肿瘤数据库之一,其收集了大量循证医学的相关数据,为肿瘤医学研究提供了宝贵的数据支持[5]。近年来,国内外众多研究者利用机器学习算法对SEER数据库进行了数据挖掘,构建了多种肿瘤的临床预后模型[6-9]。logistic回归、决策树、支持向量机、随机森林和人工神经网络是5种常用的机器学习算法,在诸多领域具有广泛的应用。本研究基于SEER数据库2010-2015年浸润性乳腺癌患者的有效数据,利用上述机器学习算法筛选浸润性乳腺癌预后的影响因素并建立预后模型,以期为临床医师判断浸润性乳腺癌患者的治疗效果和预后提供依据。
1 资料和方法 1.1 数据采集本研究数据来源于SEER数据库中2010-2015年浸润性乳腺癌患者的临床和病理资料。根据纳入和排除标准,从26 230例乳腺癌患者中共筛选出符合条件的晚期浸润性乳腺癌患者24 584例。纳入标准:(1)具有完整的临床及病理资料;(2)病理确诊为浸润性乳腺癌;(3)诊断年份为2010年1月至2015年12月。排除标准:随访资料缺失的患者。
本研究的研究终点为患者的临床死亡。
1.2 数据预处理在乳腺外科医师指导下,本研究选取21个变量作为输入变量,以浸润性乳腺癌患者是否发生死亡作为输出变量。数据预处理应使数据尽可能满足建模要求,并在满足要求的前提下尽量简化数据形式。SEER数据库存在缺失变量,且所选变量中,部分变量存在分类冗余情况。为降低建模分析的复杂程度,根据既往研究[10],对本研究相关细项进行合并赋值,将连续性变量年龄按是否大于60岁重新编码为二分类变量,连续性变量肿瘤大小按是否大于60 mm重新编码为二分类变量,多分类变量转换为二分类变量。变量赋值情况见表 1。
|
|
表 1 变量赋值 Tab 1 Variable assignment |
1.2 模型建立 1.2.1 logistic回归模型
logistic回归模型的基本架构直接来自线性回归模型[11]。具有n个自变量的logistic回归模型如下:
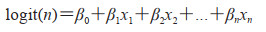
|
(1) |
其中x1, x2, ..., xn为每个样本的n个特征,β1, β2, ..., βn为其对应的系数,β0为常数项。从形式上看,logistic回归方程与一般线性回归方程的形式相同,可用类似方法解释方程中系数的含义。即当其他解释变量保持不变时,解释变量每增加1个单位,将引起logit(n)平均增加(或减少)βn个单位。因变量是二分类变量时,通常采用二值结果变量的多重logistic回归分析。本研究应用R 4.2.0软件建立logistic回归模型。
1.2.2 决策树模型决策树模型是将总体研究样本通过某些特征(自变量取值)分成若干相对同质的子样本[12],每一个子样本内部因变量的取值高度一致,相应的变异尽量落在不同子样本间。所有的树模型算法都遵循这一原则。设置的最大深度为5,当叶节点样本数小于50时,停止树生长。本研究应用R 4.2.0软件建立决策树模型。
1.2.3 支持向量机支持向量机是20世纪90年代开发的一种有监督机器学习算法[13]。当数据集线性不可分时,支持向量机可通过映射函数将线性不可分的数据从原始特征空间映射到一个更高维的特征空间,在高维空间中找到一个最佳的分隔平面(最大间隔超平面),从而将不同类别的样本区分开来。支持向量机模型在处理非线性可分、高维数据分类问题和泛化能力方面都表现出特有的优势。本研究应用R 4.2.0软件建立支持向量机模型。
1.2.4 随机森林随机森林是由Breiman[14]提出的基于树模型构建的一种常见的集成学习模型,在医学研究中已经得到广泛应用[15]。集成学习通过综合多个弱分类器的分类结果,可进一步提升模型的性能。集成学习模型的性能一般优于单个的基础分类器。随机森林使用决策树作为基础分类器,待分类样本的分类结果由所有相互独立的决策树的分类结果投票决定。随机森林模型有2次随机化过程——训练样本随机化和特征随机化。随机森林在处理高维数据问题时更有优势,也提供了更强大的泛化能力。本研究应用R 4.2.0软件建立随机森林模型。
1.2.5 人工神经网络人工神经网络是一种模拟人脑思维的计算机建模算法[16]。本研究采用基于感知器算法的人工神经网络模型,结构上可划分为输入层、隐含层和输出层。隐含层的层数和每层节点数决定了神经网络的复杂程度。本研究需对浸润性乳腺癌患者预后情况进行二分类判定,这就要确定一个超平面,位于超平面上部的所有样本点属于一种情况,位于下部的属于另一种情况。本研究应用R 4.2.0软件建立人工神经网络模型。
1.3 模型评价指标在临床医学上,常用灵敏度、特异度及分类准确度3个指标判定机器学习算法正确分类的能力[17]。这3个指标的取值均在0~1之间,取值越大分类效果越好。ROC是基于灵敏度和特异度的一种直观的评价方式,AUC越大分类效果越好,AUC取值大于0.7时,诊断价值较高[18]。本研究以灵敏度、特异度、准确度、AUC作为模型的评价指标。
1.4 抽样与验证方法基于原始数据,发生危险事件采用过抽样与欠抽样联合的抽样方法[19],设置合适的抽样比例 P=0.5,保证两组样本数量基本平衡。
按照7∶3的比例将数据随机分成训练集(n=17 209)和测试集(n=7 375),训练集用于模型训练,测试集用于模型验证。
1.5 统计学处理应用R 4.2.2软件进行数据分析。分类变量采用频数和百分率表示,组间比较行χ2检验。将训练集单因素分析中差异有统计学意义的变量纳入多因素logistic回归分析,筛选影响患者预后的重要变量。将影响患者预后的变量应用于原始数据、抽样数据分别构建logistic回归模型、决策树模型、支持向量机模型、人工神经网络模型,并在测试集中进行比较。基于多因素logistic回归分析变量重要性排序筛选的变量应用于抽样数据创建精简模型并进行模型比较。检验水平(α)为0.05。
2 结果 2.1 患者的临床病理特征经单因素分析后初步纳入的变量有年龄、种族、组织分级、T分期、N分期、M分期、骨转移、脑转移、肝转移、肺转移、多灶性、婚姻状况、雌激素受体表达状态、孕激素受体表达状态、人表皮生长因子受体2表达状态、肿瘤大小、化疗、放疗和手术治疗(均P<0.05,表 2)。在单因素分析基础上经多因素logistic回归分析,根据回归系数绝对值进行变量重要性排序,变量重要性排序前7个依次为组织分级、T分期、N分期、M分期、脑转移、HER-2表达状态、手术治疗。
|
|
表 2 训练集中浸润性乳腺癌患者的临床病理特征 Tab 2 Clinicopathological features of patients with invasive breast cancer in training set |
2.2 原始数据模型性能
采用原始数据创建模型,不同算法构建模型在训练集的灵敏度为0.24~0.46,特异度为0.69~0.99,准确度为0.64~0.91,AUC为0.512~0.915;在测试集的灵敏度为0.25~0.36,特异度为0.68~0.97,准确度为0.63~0.87,AUC为0.512~0.769。结果显示随机森林、人工神经网络、logistic回归构建模型的预测效能较好。见表 3。
|
|
表 3 基于原始数据不同算法构建模型的性能评价 Tab 3 Performance evaluation of the model constructed based on different algorithms of original data |
2.3 抽样数据模型性能
采用抽样数据创建模型,不同算法构建模型在训练集的灵敏度为0.50~0.80,特异度为0.61~0.88,准确度为0.55~0.84,AUC为0.555~0.841;在测试集的灵敏度为0.50~0.76,特异度为0.60~0.82,准确度为0.55~0.79,AUC为0.548~0.793。结果显示随机森林、人工神经网络构建模型的预测效能较好。见表 4。
|
|
表 4 基于抽样数据不同算法构建模型的性能评价 Tab 4 Performance evaluation of the model constructed based on different algorithms of sampling data |
2.4 抽样数据精简模型性能
为降低模型复杂程度,根据多因素logistic回归分析结果,选取组织分级、T分期、N分期、M分期、脑转移、HER-2表达状态、手术治疗这7个变量,采用抽样数据构建精简模型,不同算法构建模型在训练集的灵敏度为0.42~0.59,特异度为0.83~0.87,准确度为0.63~0.72,AUC为0.647~0.739;在测试集的灵敏度为0.42~0.73,特异度为0.66~0.86,准确度为0.62~0.71,AUC为0.647~0.734。在训练集和测试集中,人工神经网络模型的AUC均高于其他4个模型,说明人工神经网络模型预测效能较好。见表 5。
|
|
表 5 基于抽样数据不同算法构建的精简模型性能评价 Tab 5 Performance evaluation of simplified model constructed based on different algorithms of sampling data |
2.5 对浸润性乳腺癌预后影响最大的因素
从预测模型评价结果可以发现,随机森林和人工神经网络模型的预测准确性较高,随机森林残差平方和变化结果显示,与浸润性乳腺癌患者是否发生死亡相关的5个影响最大因素排名依次为M分期、T分期、组织分级、是否进行手术治疗、N分期(变量对分类树节点观测值的异质性影响百分比分别为75.63%、66.05%、62.08%、60.56%、58.23%)。
3 讨论本研究以SEER数据库中2010-2015年乳腺癌患者生存状态为目标,分别利用logistic回归、决策树、支持向量机、随机森林、人工神经网络算法建模并加以分析。为保证样本的均衡性,本研究采取过抽样与欠抽样联合的抽样方法,按照7∶3比例将数据随机分成训练集和测试集。结果表明,采用原始数据构建模型的灵敏度较低、特异度较高,主要原因是结局事件发生阳性比例较低所致。采用抽样数据构建模型的灵敏度、特异度、准确度均较高,经过处理后的平衡数据集的预测效果优于原始数据集,提示二分类数据集的不平衡性会降低机器学习的预测能力[20]。采用抽样数据构建精简模型的准确度、AUC稍下降,但预测准确度均大于0.7(除SVM模型外),即该模型的区分能力较好[18],认为筛选出的变量可作为浸润性乳腺癌预后显著的预测因子。精简模型的优点在于当患者相关指标不明确时,仍可以对预后进行准确预测,对于临床实践具有重要的意义。本研究找出了5个对浸润性乳腺癌预后影响最大的因素(M分期、T分期、组织分级、是否进行手术治疗、N分期),与临床研究经验[3, 21-22]相符,可为浸润性乳腺癌治疗及预后评价提供理论依据,辅助临床医师进行决策。
近年来,人工智能在医学领域的应用发展迅速。机器学习被认为是人工智能技术的一个子集,在临床实践中,机器学习预测模型的应用越来越广泛。支持向量机和logistic回归模型在大量研究中被广泛地应用于慢性疾病诊断[23]。浸润性乳腺癌的预测模型较多,但是基于机器学习的预测模型较为少见,本研究比较了5种机器学习模型,结果提示,随机森林和人工神经网络算法构建的模型对浸润性乳腺癌预后情况的预测效能较好。
本研究存在以下不足:(1)本研究采用的SEER数据库虽然数据量大、涵盖肿瘤种类多,但数据不包含相关检查指标,因此本研究纳入患者的指标不够充分;(2)SEER数据库中部分指标存在缺失值;(3)没有进行外部验证。
综上所述,本研究基于SEER数据库构建的浸润性乳腺癌预后模型可有效评估患者预后,可作为临床决策的重要参考工具。但由于SEER数据库的缺点,如指标不够丰富、某些数据存在缺失值等,未来仍需要更多的临床研究对模型的外推适用性进一步验证。
| [1] |
SUNG H, FERLAY J, SIEGEL R L, et al. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries[J]. CA Cancer J Clin, 2021, 71(3): 209-249. DOI:10.3322/caac.21660 |
| [2] |
郑莹, 吴春晓, 张敏璐. 乳腺癌在中国的流行状况和疾病特征[J]. 中国癌症杂志, 2013, 23(8): 561-569. DOI:10.3969/j.issn.1007-3969.2013.08.001 |
| [3] |
宋效清, 谢裕赛, 邱雪杉. 乳腺癌患者预后评估模型的构建[J]. 大连医科大学学报, 2021, 7(1): 29-37. DOI:10.11724/jdmu.2021.01.06 |
| [4] |
THORAT M A, LEVEY P M, JONES J L, et al. Prognostic and predictive value of HER2 expression in ductal carcinoma in situ: results from the UK/ANZ DCIS randomized trial[J]. Clin Cancer Res, 2021, 27(19): 5317-5324. DOI:10.1158/1078-0432.CCR-21-1239 |
| [5] |
章鸣嬛, 陈瑛, 汪城, 等. 美国国立癌症研究所SEER数据库概述及应用[J]. 微型电脑应用, 2015, 31(12): 26-28, 32. DOI:10.3969/j.issn.1007-757X.2015.12.010 |
| [6] |
MOURAD M, MOUBAYED S, DEZUBE A, et al. Machine learning and feature selection applied to SEER data to reliably assess thyroid cancer prognosis[J]. Sci Rep, 2020, 10(1): 5176. DOI:10.1038/s41598-020-62023-w |
| [7] |
YU C, ZHANG Y. Establishment of prognostic nomogram for elderly colorectal cancer patients: a SEER database analysis[J]. BMC Gastroenterol, 2020, 20(1): 347. DOI:10.1186/s12876-020-01464-z |
| [8] |
尹玢璨, 辛世超, 张晗, 等. 基于SEER数据库应用贝叶斯网络构建亚洲肿瘤患者预后模型——以非小细胞肺癌为例[J]. 数据分析与知识发现, 2017, 1(2): 41-46. |
| [9] |
韦英婷, 覃家盟, 樊金莲, 等. 基于深度学习算法开发和验证的肝细胞癌预后预测模型: 一项大样本队列和外部验证研究[J]. 中国癌症防治杂志, 2021, 13(3): 294-300. DOI:10.3969/j.issn.1674-5671.2021.03.13 |
| [10] |
陈莉莉, 石菊芳, 刘玉琴, 等. 基于人群的乳腺癌预后参数研究现状[J/CD]. 中华乳腺病杂志(电子版), 2018, 4(6): 370-372.
|
| [11] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 26.
|
| [12] |
KRZYWINSKI M, ALTMAN N. Classification and regression trees[J]. Nat Methods, 2017, 14: 757-758. DOI:10.1038/nmeth.4370 |
| [13] |
BOSER B E, GUYON I M, VAPNIK V N. A training algorithm for optimal margin classifiers, in proceedings of the fifth annual workshop oncomputational learning theory[C]. Pittsburgh: Association for Computing, 1992: 144-152.
|
| [14] |
BREIMAN L. Random forests[J]. Mach Learn, 2001, 45: 5-32. DOI:10.1023/A:1010933404324 |
| [15] |
张华, 陶立元, 赵一鸣. 随机森林算法的原理及其在临床研究中的应用[J]. 中华儿科杂志, 2021, 59(9): 798. DOI:10.3760/cma.j.cn112140-20210720-00602 |
| [16] |
袁筱祺, 朱乐兰, 高玮, 等. 基于神经网络的上海市中老年人群胆囊结石风险预测模型研究[J]. 卫生软科学, 2021, 35(12): 28-33. DOI:10.3969/j.issn.1003-2800.2021.12.006 |
| [17] |
张华, 陶立元, 赵一鸣. 临床研究中预测模型的效能评价[J]. 中华儿科杂志, 2018, 56(9): 719. DOI:10.3760/cma.j.issn.0578-1310.2018.09.022 |
| [18] |
ALBA A C, AGORITSAS T, WALSH M, et al. Discrimination and calibration of clinical prediction models: users' guides to the medical literature[J]. JAMA, 2017, 318(14): 1377-1384. DOI:10.1001/jama.2017.12126 |
| [19] |
吴磊, 房斌, 刁丽萍, 等. 融合过抽样和欠抽样的不平衡数据重抽样方法[J]. 计算机工程与应用, 2013, 49(21): 172-176, 185. |
| [20] |
李承圣, 包绮晗, 郝晓燕, 等. 基于随机森林算法的胰腺癌术后预测模型构建[J]. 吉林大学学报(医学版), 2022, 48(2): 426-435. DOI:10.13481/j.1671-587X.20220220 |
| [21] |
李聪, 娄春, 任延律, 等. 70岁以上女性乳腺癌临床病理特征及预后分析[J]. 中国普通外科杂志, 2015, 24(11): 1547-1552. DOI:10.3978/j.issn.1005-6947.2015.11.010 |
| [22] |
张圣泽, 孙献甫, 黄涛, 等. 326例70岁以上女性乳腺癌患者临床病理特征及预后分析[J]. 中华肿瘤防治杂志, 2020, 27(8): 631-635. DOI:10.16073/j.cnki.cjcpt.2020.08.08 |
| [23] |
BATTINENI G, SAGARO G G, CHINATALAPUDI N, et al. Applications of machine learning predictive models in the chronic disease diagnosis[J]. J Pers Med, 2020, 10(2): E21. DOI:10.3390/jpm10020021 |
 2024, Vol. 45
2024, Vol. 45


