2. 中国中医科学院广安门医院风湿病科, 北京 100053
2. Department of Rheumatology, Guang'anmen Hospital, China Academy of Chinese Medical Sciences, Beijing 100053, China
类风湿关节炎(rheumatoid arthritis,RA)是一种常见的自身免疫性风湿疾病,主要特征表现为慢性关节滑膜病变,通常影响手、膝和腕关节[1]。有数据显示我国RA患病率为0.2%~0.4%[2]。目前与RA相关的中医研究主要集中在RA病因、发病机制、辨证分型、证候与实验室指标的相关性、临床治疗和疗效评估等方面[3]。研究RA中医证候规律能为中医辨证论治提供依据[4]。“至少1个关节存在滑膜炎且不是由其他疾病引起”是RA的诊断标准之一,这一条要求有利于RA的诊断分类和有效治疗[5]。中医证候的诊断是通过提取中医四诊信息中证候判别的症状并进行分类的过程。临床RA中医证候特征表现为多标签属性,设计一个高效且准确的多标签分类模型,对RA证候诊断具有重要意义。
深度学习神经网络具有强大的特征提取能力,可以有效提取医学临床数据深层特征。Hügle等[6]提出了一种基于递归神经网络的自适应网络(AdaptiveNet)模型,用于RA的疾病进展预测,该方法采用长短期记忆网络提取临床RA样本间的长期依赖关系,取得了较好预测精度,但RA样本仅包括历史信息与实验室指标。Law和Ghosh[7]提出了一种级联神经网络模型,组合堆叠式自动编码器和极限学习机实现多标签分类,通过自动编码器的特征编码技术增强样本差异性和减少多标签输入表征,采用极限学习机计算类别分数并实现软分类。Hassan等[8]针对心血管自主神经病变构建了一种多级融合预测模型,该模型结合了特征选择和多模态特征融合技术,利用多类ROC曲线AUC值选择重要特征,并融合生成新的数据集,该方法虽然具有较好的分类精度,但不完全依赖原始数据特征,无法体现RA中医证候多标签数据特点。Pleiter等[9]在量表数据中引入新的后门攻击策略,将专为联合学习设计的后门攻击调整为集中式设置,还开发了2种隐形攻击变体,为保护深度神经网络(deep neural network,DNN)模型免受量表数据后门攻击提供有效支持。
多标签分类任务的机器学习方法主要包括算法自适应法和问题转换法[10]。算法自适应法扩展了现有的单标签分类方法,以适应多标签数据[11]。多标签K最近邻(multi-label K-nearest neighbor,ML-KNN)通过改进K最近邻算法[12]将一级和二级邻域信息结合解决多标签问题。排序支持向量机使用成对排序,根据结果与特定查询的关联度自适应排序结果[13]。随机k-标签集(random k-labelsets,RakEL)将初始标签集分解为若干随机子集,并利用标签幂集(label powerset,LP)训练相应的分类器[14]。该方法通过改进单标签方法实现多标签分类,却完全忽略了标签间的相关性。问题转换是将多标签分类问题转化为多个单标签二分类问题,如二进制关联(binary relevance,BR)[15]和分类器链(classifier chain)[16]。BR方法将每个标签作为一个独立的二进制分类问题,但未考虑标签间的相关性。分类器链则利用标签集的输入顺序与局部标签的关联信息构建一个链状结构,但不同的标签集顺序和错误传播会影响分类器链的预测性能。Eskandari和Ghassabi[17]提出了一种基于信息论滤波器的多标签特征选择方法,通过协同算法和问题转换策略对特征进行排序,同时考虑个体标签的影响及抽象标签空间中的判别潜力。Lou等[18]通过改进模糊系统结构并利用模糊规则对特征和标签之间的关系进行建模,提出了一种新的多标签分类方法,其能够有效地学习多标签分类中标签和特征之间的隐藏关系,提高了分类性能。分类器链的分类能力依赖于标签相关性。Zhang等[19]在多标签文本分类中用成对标签共现预测(pairwise label co-occurrence prediction)和条件标签共现预测(conditional label co-occurrence prediction)实现共现预测任务,增强了标签相关性,减少了标签过拟合和误差传播,实验结果表明该方法具有较好的学习标签相关性。Li等[20]研究了有噪声的多标签转移矩阵的估计问题,提出了一种新的转移矩阵估计器,充分利用标签相关性,实现了多标签数据集转移矩阵准确估计。Mencía等[21]提出了一种基于随机决策树的预测方法,可以动态选择标签序列来增强标签之间的依赖关系。Han等[22]通过挖掘标签之间的统计关系构建了一个邻接矩阵来对标签相关性进行建模,其使用了图卷积网络学习相邻节点间信息传播规律,实验结果表明模型具有较好的效果。Bakhshi和Can[23]提出一种多标签数据流分类方法,引入基于单标签分类器预测的加权机制,并考虑二进制标签之间的相关性,使模型的有效性和效率达到均衡。
本文针对临床RA中医证候多标签样本,提出了一种基于特征提取的集成神经网络模型——集成神经网络链(feature extraction network,FEN)。该模型使用DNN构建一个基分类器特征提取分类器(feature extraction classifier,FEC),能够提取RA数据中的特征层次结构,学习输入和输出之间的复杂关系;根据协方差理论衡量标签间的相关性,确定特征提取分类器链(feature extraction classifier chain,FECC)的标签集输入,减少了弱相关或负相关标签之间的干扰;还采用集成学习方法构建多条关联分类器链,减少了不合理的标签序列对分类的影响,提高了分类性能。
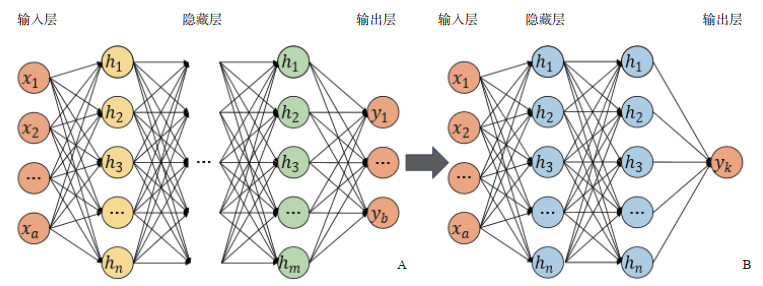
1 基于集成学习的多标签分类器FEN模型的构建 1.1 基于DNN的特征提取基分类器FEC分类器链是解决多标签分类问题的一种常用方法,一般采用基分类器学习数据特征,而基分类器由基于序列最小最优化算法的支持向量机构成。在传统神经网络模型中,循环神经网络主要用于处理序列数据,在自然语言处理领域应用广泛,卷积神经网络在数字图像处理领域取得了巨大的成功,DNN则更适合处理临床医学表格数据。在处理多标签数据时,需要考虑数据样本的复杂性和关联性,DNN具有强大的数据特征学习能力,能学习到标签数据间的深层特征。利用DNN构建一个基分类器,可以学习RA中医证候样本的深层特征。DNN内部的神经网络层可以分为3类,分别为输入层、输出层和隐藏层(图 1A)。神经网络中的隐藏层能够提取数据的深层特征,并且随着隐藏层层数的增加其特征提取能力增强。然而,隐藏层层数过多会导致网络模型过拟合等问题。本研究设计了一个4层的网络模型FEC,如图 1B所示。网络的输入层为第1层,中间2层为隐藏层,最后1层为输出层,同时修改了输出层的节点个数,将该网络作为FEN模型中的基分类器FEC。其中,xa表示第a个输入单元,hn和hm分别表示第n个和第m个隐藏层单元,yb和yk分别为第b个和第k个输出单元,k对应第k个标签。隐藏层由线性层(linear)和ReLU激活函数构成,输出层的激活函数为Sigmoid。
|
图 1 DNN(A)和FEC(B)的网络结构 Fig 1 Network structure of DNN (A) and FEC (B) DNN:深度神经网络;FEC:特征提取分类器. xa:第a个输入单元;hn:第n个隐藏层单元;hm:第m个隐藏层单元;yb:第b个输出单元;yk:第k个输出单元:k:第k个标签. |
1.2 基于标签相关性的FECC
传统的分类器链结构由输入的标签集顺序确定标签链,链中每个基分类器的输入空间均接受先前的基分类器输出结果,并训练一个标签。分类器链可以让每个基分类器学习标签间的局部关联特征,使分类器具有更好的分类性能。假设2个强正相关的标签可以相互学习更多的特征,而2个不相关或负相关的标签可能会增加分类器训练时的数据冗余度,甚至发生误差传播影响分类精度。因此,解决不相关或负相关的标签问题可以有效提高分类器链的分类性能。
单个FEC可以学习多标签数据的深层特征,却忽略了标签间的关联信息。使用链式结构将FEC连接起来构建一条FECC能够有效学习不同RA中医证候之间的关联信息。本研究在标签集y=[y1, …, yi, …, yj, …, yk]输送到分类器链前,使用一种相关系数衡量标签间的相关性。首先利用协方差公式度量2个标签间的相关性,协方差计算公式为
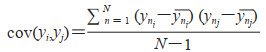
|
(1) |
其中N为实例个数,yi和yj分别为2个标签,标签yi和yj的相关性强弱取决于cov(yi, yj)值;协方差受标签尺度影响,从协方差中引出相关系数ρ来衡量标签相关性,ρ计算公式为
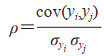
|
(2) |
其中σyi和σyj分别为2个标签的方差。方差计算公式为
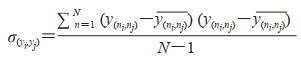
|
(3) |
在分类器链中设置标签阈值,即
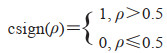
|
(4) |
若ρ大于阈值0.5,标签yi和标签yj的正相关性较强,即为强正相关标签,将基分类器FECi的输出结果输入基分类器FECj的输入空间;否则标签yi和标签yj不相关或弱正相关甚至负相关,基分类器FECi的输出结果不输入基分类器FECj的输入空间。
FECC增强了标签的局部相关性,也减少了分类器冗余,具有更好的分类性能。对于标签间存在相关性的数据集,通过考虑标签间相关性强弱来调节基分类器输入,使其合理地利用标签间的关联信息,减少分类器链的冗余度和误差传播,增强模型的分类能力。图 2所示为FECC,该分类器链中共有8个FEC。通过衡量标签间的相关性重新确定FECC中的标签集顺序y=[y11, y21, …, y81],每个基分类器FEC的输入为Xs=[X, (y11', …, ys-11')],其中1≤s≤8。例如,若标签y31与标签y41的相关性较弱,基分类器FEC3的输出y31'不会作为输入结果送入基分类器FEC4的输入空间,基分类器FEC4的输入空间为X4=[X, (y11', y21')];若标签y21和标签y71的相关性较弱,则基分类器FEC2的输出y21'不能作为输入结果送入基分类器FEC7的输入空间,基分类器FEC7的输入空间为X7=[X, (y11', y31', y41', y51', y61')]。
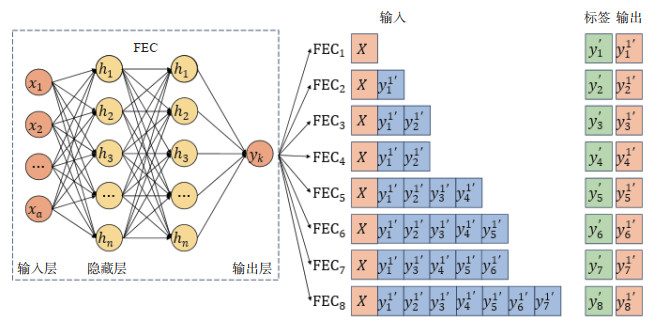
|
图 2 FECC结构图 Fig 2 Structure diagram of FECC FECC:特征提取分类器链;FEC:特征提取分类器.xa:第a个输入单元;hn:第n个隐藏层单元;yk:第k个输出单元:k:第k个标签;y':输入到FEC中的乱序标签集. |
1.3 集成学习融合策略
分类器链能够学习标签间的局部关联信息,对于多标签数据具有较好的分类效果,但不同的标签集顺序也会影响分类器链的分类性能。与单一分类模型相比,集成学习模型结合了多个弱模型预测结果,具有更高的分类能力。典型的集成学习方法包括袋装法(bagging)和提升法(boosting)。袋装法是指对原始数据集有放回的随机抽样,采用投票机制,将每个基学习器分类的结果进行统计,然后根据投票结果确定最终的分类标签。提升法为各模型的预测结果赋予不同的权重,加权求和结果作为最终结果。本研究采用集成学习方法,对FECC进行扩展,随机打乱输入到分类器链的标签集顺序,每个标签的分类结果由每条链对应的子标签分类结果投票决定。
图 3所示为FEN模型结构,基本思想是构建M条FECC,每条由K个基分类器FEC连接构成。其中,第m条链的第k个基分类器可表示为FECkm。由于RA中医证候的标签数目为8,则每条分类器链中有8个基分类器FEC。确定相关性强弱的标签后,将新的标签集Y=[yα1, yα2, …, yα8]随机排序后输入FECC中,最终每个标签的分类结果由每条链中相应子标签分类结果投票决定。

|
图 3 FEN模型结构图 Fig 3 Structure diagram of FEN model FEN:集成神经网络链;RA:类风湿关节炎;FEC:特征提取分类器;FECC:特征提取分类器链.xn:第n个样本;fl:第l个特征;FECCm:第m个FECC;FEC1m~FEC8m:第m个FECC中第1~8个FEC;y1m~y8m:第m个FECC中第1~8个FEC的对应标签:y1m'~y8m':第m个FECC中第1~8个FEC的输出标签. |
在FEN模型中,扩展了M条FECC,每条有K个基分类器FEC。在模型训练中首先通过协方差理论衡量标签间的相关性,确定新的标签集Y=[yα1, yα2, …, yαk]。将新的标签集随机打乱顺序分别输入到集成分类器链(ensemble classifier chain,Ecc)中。假设第m条FECC的随机标签集序列为Ym=[yα1m, yα2m, …, yαkm]。对于第m条FECC的第i个基分类器的输入为Xim=[X, (yα1m', …, yαi-1m')],对应的函数为fim (Xim),输出结果为Oαim,输出结果乘以前一个的输出为
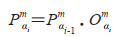
|
(5) |
预测结果为
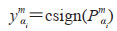
|
(6) |
在模型测试中,对于第αk个标签,其最终输出为M个基分类器输出的加权求和,即
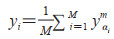
|
(7) |
最终得到的预测结果为Y=[y1, y2, …, yk]。
FEN的详细算法流程如图 4所示。

|
图 4 FEN的算法流程 Fig 4 Algorithm flow of FEN FEN:集成神经网络链;FEC:特征提取分类器. |
2 实验结果与分析 2.1 RA中医证候数据集及预处理
所采用的实验数据来自中国中医科学院广安门医院1 683例RA患者的临床数据集。删除存在缺失值和错误值的病例,去除部分冗余信息如患者社会学资料、实验室指标等,保留了11种RA中医证候特征,分别为主证、兼证、主证-主症、主证-次症、兼证-主症、兼证-次症、脉象、舌色、舌形、苔质、苔色。主证是RA的主要病症,兼证是与主证在同一时间出现的兼杂病症。主证和兼证均含有相同的8种RA中医证候,分别为风湿痹阻证、寒湿痹阻证、肝肾不足证、气血两虚证、气阴两虚证、湿热痹阻证、痰瘀痹阻证、瘀血阻络证。对于每例RA患者既有主证,也可能具有兼证,即每例RA患者具有1~2个RA中医证候,因此RA中医证候分类属于多标签分类。图 5所示为1 683例患者不同主证的数量及不同主证下兼证所占比例,其中湿热痹阻证样本最多(511例),气阴两虚证最少(69例);主证为瘀血阻络证的样本中无其他兼证者占46%(38/82),既有瘀血阻络证又有兼证风湿痹阻证者占27%(22/82)。
|
图 5 1 683例类风湿关节炎(RA)患者不同主证、兼证分布 Fig 5 Distribution of different main and accompanying syndromes in 1 683 rheumatoid arthritis (RA) patients |
另外9种(主证-主症、主证-次症、兼证-主症、兼证-次症、脉象、舌色、舌形、苔质、苔色)RA中医证候特征则是RA中医证候的常见症状,本研究将这9种特征作为RA中医证候分类特征,如表 1所示。
|
|
表 1 9种类风湿关节炎(RA)中医证候特征描述 Tab 1 Feature description of 9 kinds of traditional Chinese medicine syndromes of rheumatoid arthritis (RA) |
从表 1中可以看出每个特征包括不同数量的特征条目,且这些特征条目均为离散型。为了保证结果的可靠性,对于轻微缺失值进行补零处理,并删除具有较多缺失值的样本。本研究采用one-hot编码方式将RA中医证候分类特征转换为数字特征,共491个数据特征。因此,经过处理后的数据样本包含8个标签和491个特征。使用one-hot编码将每个病例的标签和特征使用0、1的方式表示,0表示该病例没有该证候或特征,1表示该病例有该证候或特征。
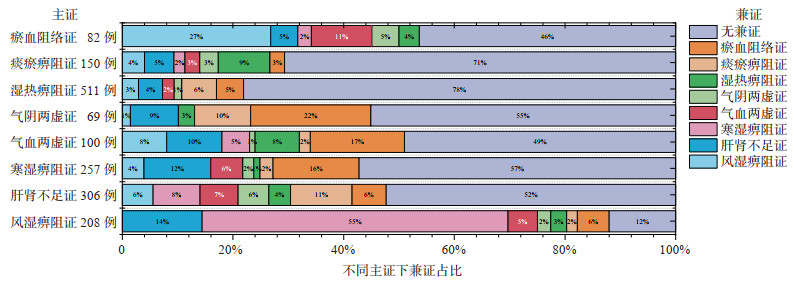
2.2 评价指标采用3种损失指标和3种性能指标评价模型的分类效果。3种损失指标分别为汉明损失(Hamming loss)、1-错误率(one-error)和排名损失(ranking loss),损失指标的值越小表明模型的分类效果越好;3种性能指标分别为准确度(accuracy)、召回率(recall)和F1值(F1-score),性能指标的值越大表明模型的分类效果越好。此外,还使用平均精度(average precision)作为多标签分类结果的评价指标,其值越大表明模型性能越好;使用几何平均值(geometric mean,G-mean)衡量模型的综合表现。各指标定义为
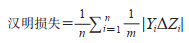
|
(8) |
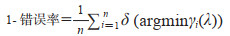
|
(9) |
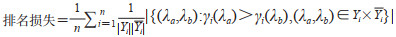
|
(10) |
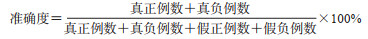
|
(11) |

|
(12) |

|
(13) |

|
(14) |
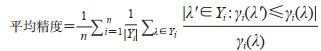
|
(15) |

|
(16) |

|
(17) |

|
(18) |
其中n为样本数,式(8)中Yi是第i个样本的真实标签集合,∆Zi表示第i个样本的预测值Z的偏移量,δ表示指示函数,argminγi(λ)表示在给定样本i的相关度评分γi(λ)中取得最小值的λ的索引,式(10)和(15)中的Yi是第i个样本的相关样本集合,Yi是第i个样本的不相关样本集合,|Yi |和|Yi|分别是它们的元素个数,λa和λb表示第i个样本与其他样本的关系,a、b代表样本在序列中的排列顺序,γi(λ)是样本i与λ的相关度评分。
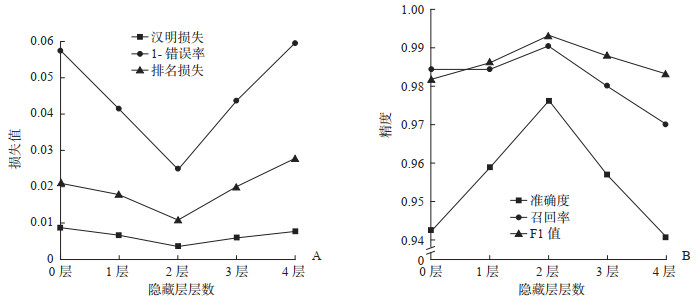
2.3 消融实验 2.3.1 FEC网络隐藏层层数对多标签分类的影响当网络隐藏层的层数较少时,模型无法学习到数据的深层特征,导致模型各项评价指标均较差。如果网络隐藏层的层数过多则会导致模型过拟合,因此需要选择合适的层数以提高模型的精度和泛化性能。图 6所示为不同隐藏层层数对模型性能的影响结果。当隐藏层层数为2时,汉明损失、1-错误率和排名损失均最低,准确度、召回率和F1值均最高,故将该隐藏层的层数作为模型FEC网络参数。
|
图 6 不同隐藏层层数的模型性能比较 Fig 6 Comparison of model performance with different hidden layers A:损失指标;B:性能指标. |
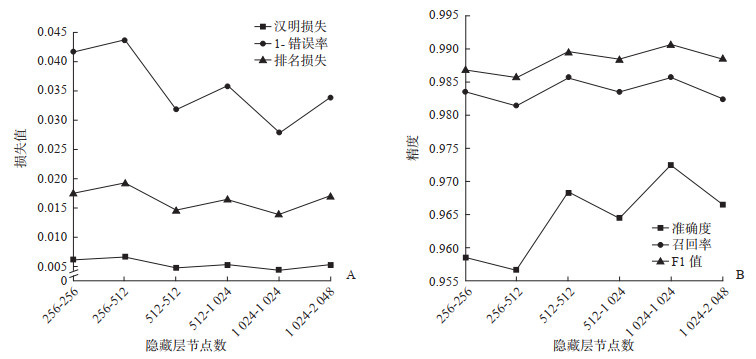
在神经网络中,隐藏层节点数对模型的性能影响很大,不仅与输入、输出层的节点数有关,更与需要解决问题的复杂程度和样本数据的特性有关。
1 683例RA样本按照7∶3的比例划分为训练集(1 178例)和测试集(505例),为了使隐藏层节点数接近训练样本数,将隐藏层节点数设置为1 024,与其他具有不同隐藏层节点数的模型的分类性能对比结果见图 7。当2层隐藏层节点数均设置为1 024时,模型的损失指标和性能指标均最优,可见当节点数接近训练样本数时模型的分类效果更好。
|
图 7 不同隐藏层节点数的模型性能比较 Fig 7 Comparison of performance among models with different number of nodes in hidden layers A:损失指标;B:性能指标. |
2.3.2 FECC标签相关性对多标签分类的影响
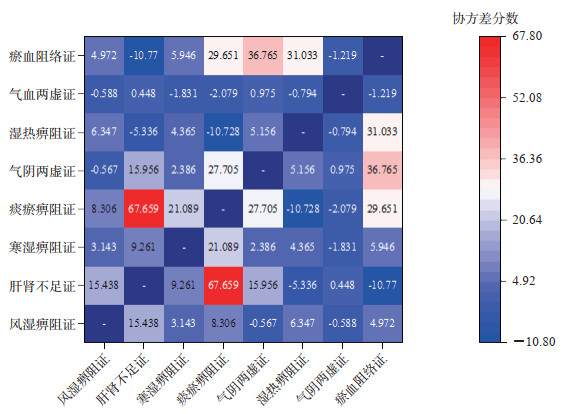
对RA多标签样本进行相关性分析,引入属性协方差描述RA中医证候任意2个标签之间的相关性,图 8展示了8个标签协方差分数。矩阵中的分数为正值表明2个标签为正相关,分数值越高说明相关性越强;分数为负值表明2个标签为负相关,分数值越小说明其反向程度越大。分析可知,痰瘀痹阻证与肝肾不足证之间具有最强的正相关性,而瘀血阻络证与肝肾不足证之间具有最强的负相关性。
|
图 8 8个标签协方差矩阵 Fig 8 Covariance matrix of 8 labels |
RA中医证候真实值与模型预测值对比结果如表 2所示。病例1和病例2均患有痰瘀痹阻证和肝肾不足证,由于这2个标签之间具有最强的正相关性,对应的基分类器输入空间都能相互接收彼此的信息,FEN和分类器链都能准确预测其真实值。病例5和病例6均患有瘀血阻络证和肝肾不足证,2个标签之间具有最强的负相关性,对于这2个病例,FEN在模型训练时,2个标签对应的基分类器输入空间不会接收彼此的信息,避免了噪声干扰和错误传播,可以正确预测其真实值;而分类器链由于负相关标签的干扰,不能同时正确预测出肝肾不足证和瘀血阻络证,对病例5只能预测出肝肾不足证,对病例6只能预测出瘀血阻络证。通过衡量标签相关性的方法可以避免噪声干扰和误差传播,有效地提高模型的预测效果。
|
|
表 2 RA中医证候真实值与模型预测值对比结果 Tab 2 Comparison of actual and predicted values of traditional Chinese medicine syndromes of RA |
2.3.3 FEN中分类器链数量对多标签分类的影响
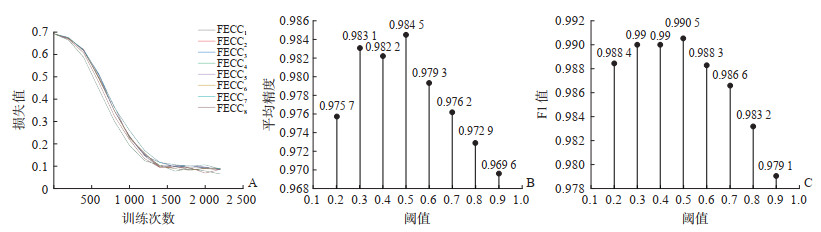
FEN模型中分类器链的数目M选取值会对分类结果产生影响。若M值过小,会减弱集成效果,不能有效减少不合理标签序列对分类结果的干扰;若M值过大,则使得模型过大,导致参数量较多,训练时间较长。根据经验值,本研究将M值设置为8,图 9A展示了M值为8时每条分类器链FECC随着训练次数增加损失值的变化曲线,图 9B、9C分别展示了FEN模型在不同阈值下针对RA中医证候样本多标签分类的平均精度和F1值。平均精度是一种基于标签排序的评估指标,在计算分类精度时考虑了标签间的相关性,能更好地衡量多标签分类器的分类性能。其中,FEN模型在标签阈值设置为0.5时平均精度达到最大值,为0.984 5。F1值作为精确率和召回率的调和平均数,可以精确地评价模型效果的优劣,当标签阈值设置为0.5时模型的效果达到最优,F1值为0.990 5。
|
图 9 FEN模型的损失曲线及不同阈值下的平均精度和F1值 Fig 9 Loss curves of FEN model and average precision and F1-scores under different thresholds A:损失曲线;B:平均精度;C:F1值. FEN:集成神经网络链;FECC:特征提取分类器链. |
2.4 交叉验证实验结果
表 3所示为FEN模型RA中医证候多标签分类交叉验证结果。采用10折交叉验证法,将1 683例样本数据分成10份,然后进行10次实验,每次实验都从这10份数据中选取其中9份作为训练集来训练模型,其余1份作为测试集(168例)用于评估模型的性能。分析可知,各项评价指标的标准差均小于0.003,实验过程中数据波动较小,每轮实验所用的数据均服从同一分布。汉明损失、1-错误率和排名损失分别为0.003 6、0.024 8和0.010 9,准确度、召回率和F1值分别为97.52%、98.92%和99.18%,说明FEN对RA中医证候样本的多标签分类具有较高的分类精度和较好的泛化性能。
|
|
表 3 1 683例RA中医证候分类10折交叉验证结果 Tab 3 10-fold cross-validation for classification of traditional Chinese medicine syndromes of 1 683 RA patients |
2.5 各种多标签分类器分类效果比较
FEN与其他7种典型多标签分类器[分类器链、LP、BR、RakEL、ML-KNN、Ecc和集成二进制关联(ensemble binary relevance,Ebr)]对168例测试集样本RA中医证候的分类效果对比结果见表 4。FEN的3种损失指标汉明损失、1-错误率和排名损失分别为0.003 6、0.024 8和0.010 9,均低于其他7种分类模型;FEN的3种性能指标准确度、召回率和F1值分别为97.52%、98.92%和99.18%,均高于其他7种分类模型,可见FEN与其他多标签分类器相比具有较高的分类精度和泛化性能。这是由于基于问题转换的多标签分类模型(BR、分类器链)将多标签分类转换为多个单标签分类,未能合理利用RA中医证候标签之间的关联性,降低了RA样本的分类精度;基于算法适应的多标签分类模型(ML-KNN、RakEL、LP)通过扩展单标签方法实现多标签分类,无法有效提取具有强关联特征的RA中医证候样本深层特征,使其分类性能较低;而集成学习方法(Ecc、Ebr)则通过集成多个单分类器仅学习部分标签之间的相关性,使分类精度降低。本研究FEN模型采用DNN结构构建基分类器FEC提取RA中医证候特征,通过计算不同标签的协方差分数划分标签的强弱关系,并采用链式结构FECC将标签输入到与之具有强相关性的标签基分类器中,充分利用了标签间的关联性,减少了数据冗余度和误差传播,而且基于集成学习方法分类器链FECC结构,减少了不合理标签序列的干扰,提高了模型的泛化性能。
|
|
表 4 各多标签分类器对RA中医证候的分类结果 Tab 4 Classification results of traditional Chinese medicine syndromes of RA by each multi-label classifier |
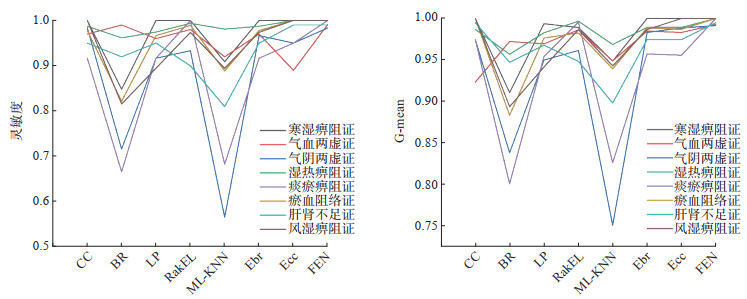
图 10为505例测试集样本中,各分类器对各子标签在灵敏度和G-mean上的分类比较结果。灵敏度衡量了模型对真正例的识别能力,本研究FEN模型判断寒湿痹阻证、湿热痹阻证、痰瘀痹阻证、淤血阻络证和风湿痹阻证的灵敏度均达到1.0,FEN能够有效地捕获并识别这些真正例。G-mean综合考虑了分类器在正负2个类别上的性能,对每个子标签的G-mean进行统计发现FEN对8个子标标签的G-mean均超过0.99,寒湿痹阻证、湿热痹阻证、痰瘀痹阻证、瘀血阻络证和风湿痹阻证的G-mean均达到1.00。FEN在标签输入时避免了弱相关和负相关标签的干扰,充分利用了标签间的关联性,减少数据冗余度和误差传播,对于2种评估指标,FEN均有较好的表现。而其他多标签分类器如BR和Ebr在处理高度关联标签时可能表现较差,在预测时无法正确捕捉到标签之间的关联性,从而影响灵敏度和G-mean;分类器链会按照标签顺序逐个预测每个标签,如果标签的顺序选择不当,可能无法准确地捕捉到标签之间的依赖关系;RakEL是在预测阶段随机选择一部分标签进行预测,因此可能无法充分利用所有可用的标签信息;LP的性能高度依赖于标签组合的质量和覆盖率,如果标签组合不充分或质量较低,会影响灵敏度和G-mean;ML-KNN在计算标签邻居时,对样本的密度敏感,如果不同标签类别的样本密度差异较大,可能会影响预测结果,导致灵敏度和G-mean较低;Ecc通过集成多个分类器链进行预测,不同标签之间容易受到干扰,如果分类器链之间存在较高的耦合度,可能导致模型整体性能下降,影响灵敏度和G-mean。
|
图 10 各多标签分类器对RA中医证候标签分类对比结果 Fig 10 Comparison results of each multi-label classifier for classification of traditional Chinese medicine syndrome labels of RA RA:类风湿关节炎;CC:分类器链;BR:二进制关联;LP:标签幂集;RakEL:随机k-标签集;ML-KNN:多标签K最近邻;Ebr:集成二进制关联;Ecc:集成分类器链;FEN:集成神经网络链;G-mean:几何平均值. |
图 11所示为在505例测试集样本中不同分类器对每个标签分类的混淆矩阵。LP、BR模型基于单标签分类器实现多标签分类,忽略了标签之间的关联性,导致证候标签预测错误,如LP在痰瘀痹阻证、风湿痹阻证、气血两虚证和瘀血阻络证上有9例或以上预测错误,BR在气阴两虚证和瘀血阻络证上均有7例预测错误;分类器链、Ecc模型虽为集成学习策略,但忽略了标签之间的冗余,导致部分证候标签出现偏差,如分类器链在痰瘀痹阻证上有6例预测错误、瘀血阻络证上有7例预测错误,Ecc在湿热痹阻证上有6例预测错误、风湿痹阻证上有4例预测错误。表 5列出了不同多标签分类器对8个标签分类的F1值,由于分类器链、BR、Ecc、Ebr采用相关性学习和/或集成学习,在8个标签上均获得了较高的F1值;本研究模型FEN基于协方差理论的相关性并结合集成学习,相较于其他7个多标签分类器的F1值均值,在8个标签寒湿痹阻证、气血两虚证、气阴两虚证、湿热痹阻证、痰瘀痹阻证、瘀血阻络证、肝肾不足证和风湿痹阻证上的F1值分别提高了1.34%、1.21%、3.64%、1.28%、4.70%、3.19%、2.35%和2.73%。FEN在8个标签中以肝肾不足证、湿热痹阻证和痰瘀痹阻证的F1值较高,根据图 8的协方差矩阵可知肝肾不足证和湿热痹阻证之间存在负相关,FEN解决了具有负相关的标签之间的干扰,在这2个标签上的F1值最高,同时肝肾不足证和痰瘀痹阻证之间具有最强的正相关性,使在痰瘀痹阻证上也获得了较高的F1值。因此,本研究模型FEN对各标签分类的F1值优于其他多标签分类器,且能够合理地利用标签间的相关性,有效地提高了对每个标签分类的F1值。

|
图 11 各分类器针对RA中医证候分类的混淆矩阵 Fig 11 Confusion matrix of each classifier for traditional Chinese medicine syndrome classification of RA A:分类器链;B:标签幂集;C:二进制关联;D:随机k-标签集;E:集成分类器链;F:集成二进制关联;G:多标签K最近邻;H:集成神经网络链. “0”表示没有该证候;“1”表示有该证候. RA:类风湿关节炎. |
|
|
表 5 各分类器针对RA中医证候分类的F1值 Tab 5 F1-scores of each classifier for traditional Chinese medicine syndrome classification of RA |
3 算法复杂度与特征贡献度分析 3.1 算法复杂度
对于基于问题转换法的多标签分类任务计算成本包括基本分类模型和问题转换结构。其中,不同的问题转换结构可以选择不同的基分类器。本研究将Fy()定义为一个基分类器y的时间复杂度。假设多标签分类数据集有x个实例,每个实例由n个维度和k个标签组成。对于BR模型只需计算每个标签k次,因此BR模型的时间复杂度为O(kFy(x, n))。分类器链保留了BR的低复杂度,并扩展了特征空间提取标签相关性,因此分类器链的时间复杂度为O(kFy(x, n+k))。Ecc、Ebr则分别生成m个分类器链和BR,其时间复杂度分别为O(mkFy(x, n+k))、O(mkFy(x, n))。本研究模型FEN定义了基分类器FEC,并生成链式结构分类器链FECC,再采用集成学习扩展FECC,其保持了与Ecc同样的时间复杂度,即O(mkFy(x, n+k)),但获得了更好的分类精度和泛化性能。
3.2 特征贡献度主证和兼证的特征贡献度分析对于RA临床诊断和治疗具有重要的参考价值,本研究针对1 683例样本分析了RA中医证候分类中主证和兼证的特征贡献度。主证和兼证中均是主症的贡献度最高,分别为46.0%和50.8%,该特征对于RA中医证候的诊断贡献度占比超过了45%,在RA中医证候的诊断中可以作为良好的诊断指标。其次是次症的贡献度占比,分别达到了17.7%和26.4%,脉象和舌诊(苔色、舌色、苔质、舌形)的贡献度占比有所不同,主证中的脉象、苔色、舌色、苔质和舌形的贡献度占比分别为11.4%、11.1%、7.8%、4.2%和1.8%,兼证中的舌色、脉象、苔色、苔质和舌形的贡献度占比分别为7.0%、6.9%、3.4%、2.8%和2.7%。由此可见,主症和次症特征均可作为判断RA中医证候分类的重要指标,这也与临床RA诊断经验相符。因为中医学提出一种“疾病-证候-症状”关联网络以探索RA中医证候的生物学内涵[1],证候差异表达基因与其症状相关基因存在交集,因此主症、次症成为影响主证和兼证分类的主要因素。
4 总结本研究提出了一种基于集成神经网络的模型FEN,实现临床RA中医证候多标签分类。该模型构建基于DNN的基分类器提取临床RA样本的深层特征;根据协方差理论衡量标签相关性,调节分类器链的输入标签集,减少负相关或弱相关标签的干扰,合理学习局部标签的关联信息;采用集成学习方法构建多条分类器链,为每条链随机输入不同标签序列,减少不合理标签对分类的影响,提高了模型的分类精度和泛化性能。本实验结果表明,与其他多标签分类方法相比,FEN模型具有较好的分类精度和泛化性能。由于FEN模型采用了DNN和集成学习,与传统多标签分类模型相比,需要更多参数和更长训练时间,后期将重点研究如何减少模型参数量和训练时间。此外,本研究还分析了影响临床RA中医证候分类的特征贡献度,主症、次症是影响主证和兼证分类的主要因素,这为RA中医证候临床诊断提供了参考。
| [1] |
陈文佳, 巩勋, 刘蔚翔, 等. 从"病-证-症" 关联网络探索类风湿关节炎中医证候的生物内涵[J]. 中国中药杂志, 2022, 47(3): 796-806. DOI:10.19540/j.cnki.cjcmm.20211105.501 |
| [2] |
王秀芳, 赵衍振, 樊冰, 等. 早期类风湿关节炎患者的临床特点与中医证候分布规律研究[J]. 风湿病与关节炎, 2021, 10(8): 6-9. DOI:10.3969/j.issn.2095-4174.2021.08.002 |
| [3] |
柳玉佳, 王莘智, 旷惠桃, 等. 类风湿关节炎中医证候、证素分布的临床研究[J]. 北京中医药大学学报, 2020, 43(1): 79-83. DOI:10.3969/j.issn.1006-2157.2020.01.014 |
| [4] |
陈永前, 娄玉钤, 王颂歌. 冬季加重的类风湿关节炎中医证候规律分析[J]. 风湿病与关节炎, 2022, 11(7): 24-27. DOI:10.3969/j.issn.2095-4174.2022.07.005 |
| [5] |
ALETAHA D, NEOGI T, SILMAN A J, et al. 2010 rheumatoid arthritis classification criteria: an American College of Rheumatology/European League Against Rheumatism collaborative initiative[J]. Arthritis Rheum, 2010, 62(9): 2569-2581. DOI:10.1002/art.27584 |
| [6] |
HÜGLE M, KALWEIT G, HÜGLE T, et al. A dynamic deep neural network for multimodal clinical data analysis[M/OL]//SHABAN-NEJAD A, MICHALOWSKI M, BUCKERIDGE D L. Explainable AI in healthcare and medicine. Studies in computational intelligence, vol 914. Cham: Springer, 2020: 79-92. (2020-11-03) [2023-06-25]. https://doi.org/10.1007/978-3-030-53352-6_8.
|
| [7] |
LAW A, GHOSH A. Multi-label classification using a cascade of stacked autoencoder and extreme learning machines[J]. Neurocomputing, 2019, 358: 222-234. DOI:10.1016/j.neucom.2019.05.051 |
| [8] |
HASSAN M R, HUDA S, HASSAN M M, et al. Early detection of cardiovascular autonomic neuropathy: a multi-class classification model based on feature selection and deep learning feature fusion[J]. Inf Fusion, 2022, 77: 70-80. DOI:10.1016/j.inffus.2021.07.010 |
| [9] |
PLEITER B, TAJALLI B, KOFFAS S, et al. Tabdoor: backdoor vulnerabilities in transformer-based neural networks for tabular data[J/OL]. arXiv: 2311.07550. (2023-11-13) [2023-12-25]. https://doi.org/10.48550/arXiv.2311.07550.
|
| [10] |
SU J, ZHU M, MURTADHA A, et al. ZLPR: a novel loss for multi-label classification[J/OL]. arXiv: 2208.02955. (2022-08-05) [2023-06-25]. https://doi.org/10.48550/arXiv.2208.02955.
|
| [11] |
MASUYAMA N, NOJIMA Y, LOO C K, et al. Multi-label classification via adaptive resonance theory-based clustering[J]. IEEE Trans Pattern Anal Mach Intell, 2023, 45(7): 8696-8712. DOI:10.1109/TPAMI.2022.3230414 |
| [12] |
ZHANG M L, ZHOU Z H. ML-KNN: a lazy learning approach to multi-label learning[J]. Pattern Recognit, 2007, 40(7): 2038-2048. DOI:10.1016/j.patcog.2006.12.019 |
| [13] |
WANG H, XU Y. Sparse elastic net multi-label rank support vector machine with pinball loss and its applications[J]. Appl Soft Comput, 2021, 104: 107232. DOI:10.1016/j.asoc.2021.107232 |
| [14] |
TSOUMAKAS G, KATAKIS I, VLAHAVAS I. Random k-labelsets for multilabel classification[J]. IEEE Trans Knowl Data Eng, 2011, 23(7): 1079-1089. DOI:10.1109/TKDE.2010.164 |
| [15] |
GONÇALVES T, QUARESMA P. A preliminary approach to the multilabel classification problem of Portuguese juridical documents[C/OL]//PIRES F M, ABREU S. Portuguese conference on artificial intelligence. EPIA 2003. Lecture notes in computer science, vol 2902. Berlin, Heidelberg: Springer, 2003: 435-444. [2023-06-25]. https://doi.org/10.1007/978-3-540-24580-3_50.
|
| [16] |
READ J, PFAHRINGER B, HOLMES G, et al. Classifier chains for multi-label classification[J]. Mach Lang, 2011, 85(3): 333-359. DOI:10.1007/s10994-011-5256-5 |
| [17] |
ESKANDARI S, GHASSABI S. Multi-label feature selection using adaptive and transformed relevance[J/OL]. arXiv: 2309.14768. (2023-09-26) [2023-12-25]. https://doi.org/10.48550/arXiv.2309.14768.
|
| [18] |
LOU Q, DENG Z, XIAO Z, et al. Multilabel takagi-sugeno-Kang fuzzy system[J]. IEEE Trans Fuzzy Syst, 2022, 30(9): 3410-3425. DOI:10.1109/TFUZZ.2021.3115967 |
| [19] |
ZHANG X, ZHANG Q W, YAN Z, et al. Enhancing label correlation feedback in multi-label text classification via multi-task learning[J/OL]. arXiv: 2106.03103. (2021-06-06) [2023-06-25]. https://doi.org/10.48550/arXiv.2106.03103.
|
| [20] |
LI S, XIA X, ZHANG H, et al. Multi-label noise transition matrix estimation with label correlations: theory and algorithm[J/OL]. arXiv: 2309.12706. (2023-09-22) [2023-12-25]. https://doi.org/10.48550/arXiv.2309.12706.
|
| [21] |
MENCÍA E L, KULESSA M, BOHLENDER S, et al. Tree-based dynamic classifier chains[J]. Mach Lang, 2023, 112(11): 4129-4165. DOI:10.1007/s10994-022-06162-3 |
| [22] |
HAN Q, DU X, SUN Y, et al. Label dependencies-aware set prediction networks for multi-label text classification[J/OL]. arXiv: 2304.07022. (2023-04-14) [2023-12-25]. https://doi.org/10.48550/arXiv.2304.07022.
|
| [23] |
BAKHSHI S, CAN F. Balancing efficiency vs. effectiveness and providing missing label robustness in multi-label stream classification[J/OL]. arXiv: 2310.00665. (2023-10-01) [2023-12-25]. https://doi.org/10.48550/arXiv.2310.00665.
|
 2024, Vol. 45
2024, Vol. 45


