高血压的分级及危险分层是临床上诊断高血压经常用到的标准。高血压的分级依据血压水平来划分，主要分为3级。危险分层是在高血压分级的基础上，根据患者的危险因素和病史区分，分为低危、中危、高危、很高危。高血压是心脑血管疾病的高危因素，现已成为我国老年人最常见的慢性病之一^[1]。目前，我国高血压患者数量约为2.7亿例^[2]，但随着人口老龄化逐渐加重及高血压的诊断标准可能下调，中国高血压患者数量接近5亿，而我国高血压患者的知晓率、治疗率、控制率很低^[3]。这导致脑卒中、心肌梗死及严重的靶器官损伤等心血管疾病患者增多，医疗负担加重，所以高血压的防治刻不容缓。

近年来，随着深度学习等在医学领域应用的渗透，许多学者提出了使用人工智能技术实现高血压患者危险分层的诊断方法。崔佳嘉等^[4]通过提取梅尔频率倒谱系数（Mel-scale frequency cepstral coefficient，MFCC），并运用局部线性嵌入算法（local linear embedding）对现有的MFCC特征向量降维改进，保证能保留变压器噪声信号的有效信息。Zhang等^[5]采用9层卷积神经网络（convolutional neural network，CNN）对脉搏波进行分类，平均准确率达到了93.49%，但研究的样本量较小，缺少交叉验证支撑实验结论，模型的泛化性没有得到进一步验证。笔者团队构建了基于CNN‐双向长短时记忆（bi‐directional long short‐term memory，BiLSTM）结构的高血压脉诊分类网络，该模型可以有效地提取脉诊局部及全局序列特征，其准确率可达77.17%^[6]。马明艳等^[7]使用CNN-BiLSTM网络对入侵的恶意行为进行检测，精度达到了92%。该方法在CNN和BiLSTM基础上进行融合，具有“并联”多通道融合特性，但当数据时序较长时，BiLSTM模型训练时间较长，出现特征冗余问题。杨如民等^[8]采用蝙蝠算法和随机森林算法对脉搏波信号进行分类，分类精度提高了3.4%，但该方法需要根据经验确定特征维度，且主观因素较多。张选等^[9]基于GoolgLeNet和ResNet框架提出MIRNet模型对健康和亚健康人群脉象分类，精度可达到87.84%。杨浩等^[10]运用CNN和BiLSTM对心房节拍分类，精度可达到90.21%。Ouyang等^[11]使用一种四层多任务融合CNN对2型糖尿病患者的脉搏波进行分类，精度最高可达90.6%，但当CNN层数较深时才能提取到脉搏波深层特征，容易造成梯度消失问题。Chen等^[12]采用基于基本残差块（BasicBlocks）的ResNet框架对女性脉搏波分类，判断是否处在妊娠期，预测准确率达到84%，该模型虽然在一定程度上解决了梯度消失问题，但其深度多在5层附近，无法学习到脉搏波周期内的深度时序特征。Yan等^[13]提出了一种基于脉搏波特征融合的无创血压预测方法，使用基于梯度提升决策树的回归算法预测患者的收缩压与舒张压，相较于水银血压计，这种方法虽然预测精度更高，但对穿戴设备有一定要求。本文提出了一种通过脉搏波诊断高血压患者危险层级的神经网络融合模型，该模型采用不同注意力机制进行决策融合，对采集的中医脉诊数据进行分析，从而得到患者高血压分层结果。该模型可以根据患者的脉诊数据实现对高血压层级的自主分类，为高血压层级诊断提供了新思路。

针对脉诊时域数据，本研究使用了一种改进的MFCC提取方法来获取脉搏波的频域特征。脉搏波信号的非稳定性使得传统的MFCC分析方法无法获得完整的频域特征，因此，本研究采取了一些操作以提高分析精度。首先进行预加重操作以增加高频部分的分辨率，然后进行分帧操作以保证观测单位内至少包含1个脉搏波周期^[14-15]，并选择汉明窗（hamming）进行加窗以增加帧左右两端的连续性。在脉搏波分解阶段，为了更好地分离不同模态成分的固有模态函数（intrinsic mode function）分量，本研究加入了自适应白噪声，以消除不同时间尺度成分的叠加，提高分解精度并减轻模态混叠效应。最后，采用脉搏波频域的MFCC来描述脉搏波特征，包括静态和动态特征，以提高脉搏波特征的区分性。

MFCC特征提取的过程主要包括预加重、分帧、加窗、加噪声、经验模态分解（empirical mode decomposition，EMD）、希尔伯特（Hirbert）变换、时间维度积分、Mel三角滤波器、对数运算与离散余弦变换，具体流程如图 1所示。

图 1 MFCC特征提取过程 Fig 1 MFCC feature extraction process MFCC: Mel-scale frequency cepstral coefficient; EMD: Empirical mode decomposition; DCT: Discrete cosine transform.

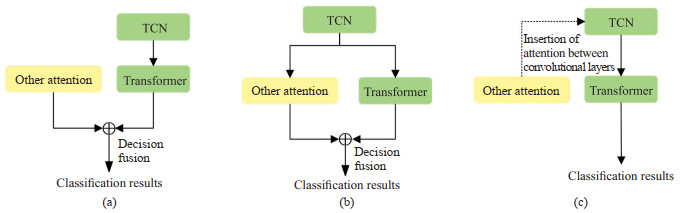
Transformer使用的注意力机制为自注意力机制（self-attention），为了使模型具有较好的泛化能力和鲁棒性，本研究考虑使用辅助注意力机制，从不同侧面弥补单个注意力的不足。考虑选择的辅助注意力机制包括压缩和激励（squeeze-and-excitation，SE）、选择性内核（selective kernel，SK）、卷积块注意力模块（convolutional block attention module，CBAM）、基于相似性的注意机制（a simple parameter-freeattention module，SimAM）和通道注意力机制（coordinate attention，CA）共5种。在原有模型的基础上讨论了3种融合方法，其模型结构如图 2所示。融合方法（a）将辅助注意力机制作为辅助模型，对2个模型分别输入脉搏波频域特征，得到的输出结果经过决策融合，再输出最终预测结果。融合方法（b）将辅助注意力机制与自注意力机制并行，2个注意力机制都接受经过时间卷积网络（temporal convolutional network，TCN）处理过的特征数据，然后再将输出结果进行决策融合，得到最终预测。融合方法（c）则将辅助注意力机制融合在TCN模块内部。本研究在TCN内部的卷积层之间插入了辅助注意力机制，以帮助提取特征之间的关联信息。经过实验，本研究最终选择了SK注意力机制作为辅助注意力机制，并采用融合方法（a），得到了表现最优的模型。

图 2 注意力机制3种融合方法（a）、（b）、（c）的结构图 Fig 2 Structural diagram of 3 fusion methods (a), (b), and (c) in attention mechanism TCN: Temporal convolutional network.

在使用融合模型后，整个网络的复杂度有所增加，模型训练速度减慢，更容易出现过拟合现象，而正则化能在训练模型的过程中防止模型出现过拟合，为此本研究分析了常见的3种正则化方式（L1、L2和Max）对模型性能的影响，但实验结果表明这3种正则化方式对模型性能没有起到帮助作用，甚至使得模型性能有所降低，不适合处理脉搏波频域数据。于是选用了间接控制训练损失的洪泛法（flooding）策略^[16]，Flooding策略使训练损失在一个小常量附近浮动，当训练损失达到合理小的值时，该方法会阻止训练损失的进一步减少，从而防止训练损失趋近于0。其表达式为

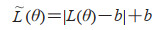
式中L(θ)表示原来的损失函数，表示处理后的损失函数，b是超参数阈值，本实验中选择参数b值为0.01。但是由于参数b的值较小，其发挥作用在模型训练的后期，本实验设想让其更早地发挥作用，故对其进行改进，提出了Floodings策略，即

式中L(θ)、含义不变，a、b是超参数，i代表一轮训练中的迭代次数，本实验选择参数a值为1，参数b值为0.01。通过加入分式项，引入额外的约束假设，该方法就可以提前控制训练损失值的下降，减轻过拟合现象，使得模型更接近全局最优解。

针对原始的脉搏波时域波形数据，本实验首先使用Sym7(SymletsN)小波基进行降噪处理，然后使用平滑先验法（smoothness priors approach，SPA）完成对原始数据的去基线漂移处理。接着使用一种改进的MFCC提取方法来获取脉搏波的36维MFCC频域特征。本实验所使用的时间卷积网络Transformer-选择性内核[temporal convolutional network Transformer-selective kernel (Floodings)，TCNT-SK(Fs)]模型结构如图 3所示，其中TCN包含有2个隐藏层，隐藏通道（hidden_channel）数分别为24和36，为了提高准确率，TCN中还加入了残差卷积的跳层连接及1×1的卷积操作；Transformer模块只使用了编码器（encoder）部分的2层结构，多头注意力参数（head）选择为4。而SK模型则先通过CNN卷积提取特征，升高数据维度至18，然后经过池化操作，输入SK网络。经过改进的MFCC提取方法得到的36维频域特征包含了输入脉搏波的包络信息和的频域边际谱信息，将频域特征分别输入TCNT和SK模型，经过各自网络模型处理后使用全连接层输出，2个模型的输出采用等权重的决策融合，计算出最终的预测结果。本实验使用的2个不同注意力机制可以从不同角度获取特征之间的联系，再将信息整合从而获得更好的模型性能。TCNT-SK(Fs)模型算法步骤如表 1所示。

图 3 TCNT-SK(Fs) 模型结构 Fig 3 TCNT-SK(Fs) model structure TCNT-SK(Fs): Temporal convolutional network Transformer-selective kernel (Floodings); SPA: Smoothness priors approach; HHT: Hilbert-Huang transform; DCT: Discrete cosine transform; MFCC: Mel-scale frequency cepstral coefficient; TCN: Temporal convolutional network; CNN: Convolutional neural network; SK: Selective kernel.

表 1 (Tab 1)

表 1 TCNT-SK(Fs) 模型训练伪代码 Tab 1 TCNT-SK(Fs) model training pseudocode Algorithm: framework for our deep learning model TCNT-SK(Fs) Input: X(n), Y(n). X: target pulse data; Y: lables (0, 1, 2); n: the number of pulse data Output: predictive labels               1.       for i＝1, 2,..., n do               2.               Xi＝preprocessing(Xi)               3.               features[i] ＝MFCC(Xi)               4.       end               1.       iteration←0               1.       while iteration＜number of epochs do               7.               initialize the model parameters               8.               iteration←iteration+1               9.               for each batch in data do               10.                       TCN layer: X1＝TCN(features)               11.                       Transformer: X1＝Trans(X1)               12.                       CNN layer: X2＝ConvReluMax(features)               13.                       SK layer: X2＝SK(X2)               14.                       FC layer: dec1＝Linear1(X1), dec2＝Linear2(X2)               15.                                       pre＝dec1+dec2               16.               end               17.      return all pre TCNT-SK(Fs): Temporal convolutional network Transformer-selective kernel (Floodings); MFCC: Mel-scale frequency cepstral coefficient; TCN: Temporal convolutional network; CNN: Convolutional neural network; SK: Selective kernel; FC: Fully connected.

表 1 TCNT-SK(Fs) 模型训练伪代码 Tab 1 TCNT-SK(Fs) model training pseudocode

TCNT-SK(Fs)模型的参数设置如表 2所示。原始脉搏波信号在提取频域特征后存在MFCC长度不一致的问题，因此采用数据中最大长度作为行标准，不足时用0补充，最大长度为200，每个维度包含36个特征，将填充好的MFCC数据作为模型的输入。本模型主要由TCNT和SK模型的决策融合组成，TCNT模型中的TCN包含2个隐藏层，其隐藏通道数分别为24和36；另外为了有效地应对长历史信息这一问题，TCN结构中使用了空洞卷积来增加感受野。空洞卷积隐含1个超参数膨胀尺寸（dilation size），表示卷积核（kernel）的间隔数量，膨胀尺寸随着层数增加呈指数增长，因此一般使用较小的卷积核就可以获得很大的感受野，这里选择卷积核为2。本实验中Transformer模型只使用了编码器Encoder部分中的2层结构，多头注意力参数为4，输入通道数对应TCN的输出为36维。而SK模型则先通过卷积层将脉搏波频域数据提升维度至18维，卷积核选择5可以获取更大感受野，接着进行池化操作，然后输入输入通道参数（input channel）为18的SK模型。2个模型均通过最后的扁平层（flatten）和线形层（linear）进行输出，再将输出结果进行决策融合得到最终的模型预测结果。

表 2 (Tab 2)

表 2 TCNT-SK(Fs) 模型超参数 Tab 2 TCNT-SK(Fs) model hyperparameters Layer Filter size Output shape Input 200×36 TCN_layer1 2×2, stride＝1 200×24 TCN_layer2 2×2, stride＝1 200×36 Transformer Head＝4, n＝2 200×36    Flatten 1×7 200    Linear 1×3 Convolutional 5×5, stride＝1 18×200×36 MaxPooling 2×2, stride＝1 18×100×18 SK Input channel＝18 18×100×18    Flatten 1×7 200    Linear 1×3 Decision fusion 1×3 TCNT-SK(Fs): Temporal convolutional network Transformer-selective kernel (Floodings); TCN: Temporal convolutional network; SK: Selective kernel.

表 2 TCNT-SK(Fs) 模型超参数 Tab 2 TCNT-SK(Fs) model hyperparameters

本实验使用脉诊仪采集脉搏波数据，样本采集前需要患者放松5 min以上，并在60 d内完成采样。采样时的触点压力根据患者脉络深浅来确定，使用的采样频率包括200 Hz、700 Hz、1 000 Hz。本实验使用上海中医药大学附属龙华医院及中西医结合医院提供的527例临床脉诊数据。男性病例223例（42.31%），平均年龄为（66.35±10.37）岁；女性病例304例（57.69%），平均年龄为（71.32±8.51）岁。该数据集包含82例（15.56%）低危、303例（57.50%）中危、142例（26.94%）高危和极高危高血压患者。

模型的训练需要确保数据维度一致性，而脉诊采样频率有200 Hz、700 Hz、1 000 Hz 3种，为此本实验将700 Hz和1 000 Hz的数据进行降采样，统一为200 Hz。然而，脉搏波的采集过程难免会受到一些干扰，数据往往存在噪声和基线漂移等问题，这可能会干扰脉搏波信号特征的提取，因此本实验对原始脉搏波信号进行了降噪和去除高频噪声等处理。因为傅里叶变换难以分辨信号在时间轴上的突变点，所以选择了多贝西（Daubechies，dbN）小波和对称多贝西（symmetric Daubechies，SymN）小波进行实验。dbN小波具有较好的正则性，该小波作为稀疏基所引入的光滑误差不容易被察觉，使得信号重构过程比较光滑。SymN具有近似对称性，可以很有效地避免相位畸变，该小波基对应的滤波器具有线性相位的特点。

本实验采用评估参数信噪比（signal noise ratio，SNR）和均方根误差（root mean square error，RMSE）评估脉搏波降噪、去除基线漂移的效果。SNR值越大、RMSE值越小说明去噪效果越好，表达式为

式中p(n)为原始信号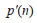，为处理后信号，N为信号长度。

表 3列出了不同小波基、不同信号长度下的评估指标SNR和RMSE值。通过对比发现，选择Symlets系列中的Sym7小波作为小波基^[17]对脉搏波信号进行降噪处理得到的效果最好，其SNR为36.867 7，RMSE为14.842 5，均是最优值。SymN小波在连续性、支集长度、滤波器长度等方面与dbN小波一致，但SymN小波具有更好的对称性，即一定程度上能够减少对信号进行分析和重构时的相位失真。

表 3 (Tab 3)

表 3 不同小波基降噪效果比较 Tab 3 Comparison of different wavelet base noise reduction effects Signal length dbN SymN SNR RMSE SNR RMSE 1 28.149 3 40.274 1 28.149 3 40.274 1 2 36.412 0 15.637 3 36.412 0 15.637 3 3 36.813 3 14.935 0 36.813 3 14.935 0 4 36.848 5 14.875 2 36.850 6 14.871 5 5 36.860 1 14.855 5 36.863 0 14.850 4 6 36.859 7 14.856 2 36.865 3 14.846 5 7 36.858 7 14.857 8 36.867 7 14.842 5 8 36.860 1 14.855 5 36.864 1 14.848 6 9 36.861 3 14.853 4 36.863 9 14.849 0 dbN: Daubechies; SymN: Symmetric Daubechies; SNR: Signal noise ratio; RMSE: Root mean square error.

表 3 不同小波基降噪效果比较 Tab 3 Comparison of different wavelet base noise reduction effects

常用的基线漂移去除方法包括SPA^[18-19]、EMD^[20-21]及低通滤波（low-pass filter），对降噪之后的数据使用这3种方法进行去基线漂移，结果如表 4所示。SPA是一种信号非线性去趋势算法，它可以保留基本的脉搏波特征。SPA算法具有较高的SNR（23.888 9）和较小的RMSE（39.683 8），更适合作为脉搏波信号的基线漂移去除处理。本实验的预处理操作即采用小波降噪和SPA分别完成对原始数据的降噪和去基线漂移处理。

表 4 (Tab 4)

表 4 不同方法去基线漂移效果比较 Tab 4 Comparison of effects of different methods for removing baseline drift Method SNR RMSE SPA 23.888 9 39.683 8 EMD 21.893 5 55.496 6 LPF 11.613 9 59.982 4 SNR: Signal noise ratio; RMSE: Root mean square error; SPA: Smoothness priors approach; EMD: Empirical mode decomposition; LPF: Low-pass filter.

表 4 不同方法去基线漂移效果比较 Tab 4 Comparison of effects of different methods for removing baseline drift

原始脉搏波样本经过小波降噪、去除基线漂移后的对比图像如图 4所示。分析图像可知，经过预处理操作后，原始脉搏波信号的基线漂移和均值均有所降低，波形噪声减少并且趋于稳定，具有较好的周期性和可区分性。

图 4 去除基线漂移、噪声后的数据波形图 Fig 4 Data waveform after removing baseline drift and noise

本实验在训练模型时均采用K折交叉验证法进行动态检验，其中K取值为5。在具体训练过程中，首先将所有数据集划分成5份，每份数据均从3类样本中随机抽取得到，不重复地每次取其中1份做验证集，其余4份做训练集进行模型训练，之后计算该模型在验证集上的各项评价指标得分。循环上述操作5次得到5次不同的实验结果，对5次实验结果进行统计计算得到平均值和方差，并作为该模型结构的最终性能指标。为了评估不同模型的性能，采用了准确度、F1值、精确率和召回率4个算法指标，以及ROC曲线及其AUC值和精确率-召回率（precision-recall，PR）曲线及其下方围成的面积平均精度来全面评价不同模型的性能。其中准确度衡量的是所有样本分类正确的比例，精确率代表对正例样本预测的准确程度，召回率表示在所有正例样本中被正确分类的比例，F1值是模型精确率和召回率的一种加权平均，综合考虑了分类模型的精确率和召回率。由于本实验为三分类问题，使用微平均（micro-averaging）方法计算各个评价指标，微平均方法是对数据集中每个实例不分类进行统计建立全局混淆矩阵并基于这个全局混淆矩阵计算相应指标的方法，因此各评价指标计算公式为

式中TP、FP、TN、FN分别是真阳性、假阳性、真阴性和假阴性样本数。

针对提取出频域特征的脉诊数据集，采用TCNT-SK(Fs)融合模型，并与Transformer、CNNT等模型相比，进行了5折交叉验证。各模型的脉搏波频域特征分类结果见表 5，分析表中数据可知，在Transformer模型中加入CNN卷积层可以有效提高模型的性能，其准确度提高了2.60%，F1值提升了1.02%，精确率提升了2.16%，召回率提升了1.65%，这是因为CNN卷积层可以对MFCC的维度特征进行整合，提取出具有局部关联关系的脉诊特征，改善了分类的效果。TCN使用了扩张卷积，层数越深、卷积窗口越大，卷积窗口中的“空孔”越多，说明这种卷积方式适合于处理与时间有关的序列。因此，TCNT模型相较于CNNT模型，将简单的CNN替换为了TCN，其在准确度上提高了0.69%，F1值提升了3.68%，精确率提升了3.56%，召回率提升了2.75%。Transformer模型使用的注意力机制为自注意力机制，为了进一步改善模型性能，本实验选择了另外一种SK注意力机制，从不同方面弥补单个注意力机制的不足。将脉搏波频域特征分别输入2个注意力模型，结果经过决策融合后输出最终预测结果，得到组合模型TCNT-SK。可以看出，TCNT-SK模型的性能相较于单个TCNT有所提升，其准确度提高了2.53%，F1值提升了3.35%，精确率提升了0.94%，召回率提升了2.21%。但是由于使用组合模型会使得网络更为复杂，梯度下降过程会出现更多的不确定性，模型有可能发生过拟合，为此引入了Flooding策略，使得训练损失在一个小常量附近浮动，防止训练损失趋近于0，本实验对其进行改进并得到了鲁棒性更强、泛化性更好的TCNT-SK(Fs)模型。相较于TCNT-SK模型，TCNT-SK(Fs)模型的准确度提高了0.89%，F1值提升了1.41%，精确率提升了0.67%，召回率提升了1.90%。

表 5 (Tab 5)

表 5 不同模型的脉搏波频域特征分类结果 Tab 5 Frequency domain feature classification results of pulse wave based on different models  n＝5, x±s Model Accuracy F1 score Precision Recall Transformer 0.879 2±0.023 4 0.842 5±0.035 1 0.875 2±0.039 1 0.854 5±0.055 0 CNNT 0.902 1±0.064 8 0.851 1±0.143 7 0.894 1±0.107 1 0.868 6±0.131 4 TCNT 0.908 3±0.034 5 0.882 4±0.039 5 0.925 9±0.025 6 0.892 5±0.040 6 TCNT-SK 0.931 3±0.008 3 0.912 0±0.011 6 0.934 6±0.008 8 0.912 2±0.007 9 TCNT-SK(Fs) 0.939 6±0.017 9 0.924 9±0.019 4 0.940 9±0.018 0 0.929 5±0.020 1 CNNT: Convolutional neural network Transformer; TCNT: Temporal convolutional network Transformer; SK: Selective kernel; Fs: Floodings.

表 5 不同模型的脉搏波频域特征分类结果 Tab 5 Frequency domain feature classification results of pulse wave based on different models

TCN是一种用来解决时间序列预测的算法。使用不同组合TCNT模型的脉搏波频域特征分类结果见表 6，分析表中数据可知，使用单层TCN时，通道数参数选择36得到的分类器分类效果较好，准确度为0.904 2，F1值为0.870 3，精确率为0.919 1，召回率为0.884 2；而继续增大通道数时分类器的分类效果反而下降，这是由于过大的通道数会提取到冗余信息，从而影响后续训练，导致模型性能下降。当使用多层TCN时，可以发现对于2层TCN模型通道数24-36的组合性能表现优于36-72的组合，这是由于通道数为36和72时提取特征信息过多，模型复杂度增加，导致模型性能降低。而3层TCN虽可以提取到深层特征，但网络深度增加，复杂度过高容易造成过拟合。

表 6 (Tab 6)

表 6 不同组合TCNT模型的脉搏波频域特征分类结果 Tab 6 Frequency domain feature classification results of pulse wave based on different combined TCNT models  n＝5,x±s Channel Accuracy F1 score Precision Recall 24 0.889 6±0.029 9 0.847 8±0.034 1 0.906 9±0.020 2 0.848 0±0.041 3 36 0.904 2±0.029 0 0.870 3±0.035 7 0.919 1±0.027 6 0.884 2±0.046 7 72 0.868 8±0.040 9 0.800 1±0.111 1 0.873 5±0.084 8 0.815 0±0.106 4 24-36 0.908 3±0.034 5 0.882 4±0.039 5 0.925 9±0.025 6 0.892 5±0.040 6 36-72 0.868 8±0.093 8 0.809 2±0.149 6 0.847 7±0.170 8 0.845 2±0.107 3 24-36-72 0.889 6±0.036 4 0.851 1±0.046 6 0.904 7±0.026 0 0.848 5±0.052 1 TCNT: Temporal convolutional network Transformer.

表 6 不同组合TCNT模型的脉搏波频域特征分类结果 Tab 6 Frequency domain feature classification results of pulse wave based on different combined TCNT models

表 7列出了不同卷积层数CNNT模型的分类结果，分析表中数据可知，随着卷积层的增加，分类结果的准确度提高，模型性能有所提升，这是由于卷积层数较少时模型无法学习到脉搏波特征之间的深层关联信息，导致模型的各项评估指标较低。而当卷积层增加到4层时，模型性能又有所降低，这是由于CNN提取到了更为抽象的深层信息，而丢失了脉搏波的表象信息，降低了模型准确度。因此，适当的卷积层数对模型的性能表现很重要。但对比TCNT模型与CNNT模型各自的最优表现发现，合适的TCNT模型（2层、通道数为24-36）拥有更好的性能表现，分类准确度为0.908 3，F1值为0.882 4，精确率为0.925 9，召回率为0.892 5（表 6）。

表 7 (Tab 7)

表 7 不同卷积层数CNNT模型的脉搏波频域特征分类结果 Tab 7 Frequency domain feature classification results of pulse wave based on CNNT models with different convolution layers  n＝5, x±s Layer Accuracy F1 score Precision Recall 1 0.885 4±0.031 6 0.839 7±0.043 1 0.904 4±0.024 6 0.844 2±0.046 5 2 0.893 8±0.017 9 0.855 4±0.026 1 0.922 2±0.018 6 0.878 9±0.036 6 3 0.902 1±0.064 8 0.851 1±0.143 7 0.894 1±0.107 1 0.868 6±0.131 4 4 0.868 8±0.085 0 0.815 3±0.136 1 0.840 7±0.170 1 0.831 0±0.084 4 CNNT: Convolutional neural network Transformer.

表 7 不同卷积层数CNNT模型的脉搏波频域特征分类结果 Tab 7 Frequency domain feature classification results of pulse wave based on CNNT models with different convolution layers

Transformer模型由编码器-解码器（encoder-decoder）两部分构成，对于本实验的分类任务只选用Encoder部分即可完成。Transformer原模型使用了多头注意力（multi-head attention）参数为8的6+6层结构，使用多头注意力是为了让模型能够关注多个不同的信息子空间，提高模型的表现。多个注意力能够让模型更好地捕捉到数据中的不同特征，有助于改善模型的性能，并帮助网络捕捉更丰富的特征信息。这种方法与在CNN中使用多个卷积核的方法类似，但它更加灵活，可以在不同的子空间中分别使用不同的权重矩阵进行操作，从而得到更好的性能提升。

在TCNT模型基础上，本实验排列组合了编码器层数分别为1、2、3和多头注意力参数分别为2、4、6共9种情况下Transformer模型的性能表现及各项评价指标，结果见表 8。随着模型层数和多头注意力参数的增加，模型性能有所提高，随后又开始下降，这是由于较少层数的模型提取信息能力有限，难以挖掘脉搏波之间的深层联系，而层数过多又会陷入信息冗余问题，很可能会得到一些抽象层次的联系，而忽略了特征之间的表象信息；多头注意力参数的影响与之类似，参数的选择需要从不同方面考虑，因为层数与多头注意力参数的增加都会明显增加模型的复杂度，导致计算量增加。但结合表中数据可知，Transformer模型本身的性能表现良好，层数与多头注意力参数对其影响有限，各组合之间的差异相对较小，本实验选择层数为2、多头注意力参数为4的TCNT模型，其准确度为0.912 5，F1值为0.883 6，精确率为0.922 3，召回率为0.901 8，复杂度在可接受范围内且性能表现最佳。

表 8 (Tab 8)

表 8 不同编码器层数与head的TCNT模型的脉搏波频域特征分类结果 Tab 8 Frequency domain feature classification results of TCNT model with different encoder layers and heads  n＝5,x±s Encoder layer Head Accuracy F1 score Precision Recall 1 2 0.906 2±0.026 4 0.875 4±0.036 6 0.920 6±0.020 8 0.878 0±0.043 9 4 0.908 3±0.034 5 0.882 4±0.039 5 0.925 9±0.025 6 0.892 5±0.040 6 6 0.904 2±0.034 5 0.882 7±0.044 1 0.918 5±0.025 9 0.884 7±0.041 1 2 2 0.904 2±0.020 2 0.868 7±0.026 4 0.918 7±0.021 8 0.877 3±0.041 4 4 0.912 5±0.019 3 0.883 6±0.022 9 0.922 3±0.021 3 0.901 8±0.029 5 6 0.902 1±0.031 3 0.866 4±0.042 3 0.913 6±0.029 6 0.871 9±0.050 5 3 2 0.908 3±0.016 7 0.883 1±0.027 0 0.917 3±0.012 7 0.889 9±0.018 0 4 0.900 0±0.016 9 0.860 6±0.023 8 0.911 1±0.021 2 0.860 9±0.027 8 6 0.904 2±0.025 9 0.867 2±0.031 9 0.912 9±0.021 1 0.858 7±0.032 6 TCNT: Temporal convolutional network Transformer.

表 8 不同编码器层数与head的TCNT模型的脉搏波频域特征分类结果 Tab 8 Frequency domain feature classification results of TCNT model with different encoder layers and heads

Transformer模型使用自注意力机制，为了改善模型性能，在原有模型的基础上，本研究选择包括SE、SK、CBAM、SimAM和CA共5种注意力机制进行实验，讨论了(a)、(b)、(c) 3种不同的注意力机制融合策略，最终得到的分类结果如表 9所示。由于SK维度无法与TCN匹配，故融合方式(c)中未进行该组合实验。实验结果表明，不同的融合方法对不同的注意力机制效果各不相同，总体来说，融合方法(a)取得了更好的表现，其中TCNT+SK的注意力机制融合方法具有很好的泛化性，其准确度为0.931 3，F1值为0.912 0，精确率为0.934 6，召回率为0.912 2，相较于进行过参数选择的TCNT模型，模型性能也有所提高，其在准确率上提高了2.06%，F1值提升了3.21%，精确率提升了1.33%，召回率提升了1.15%。这是由于多个注意力机制的使用使得模型能够从不同方面获取信息，提取到的关联信息更丰富，最后再将多方面信息综合起来，最终提高了模型性能。

表 9 (Tab 9)

表 9 不同注意力机制融合模型的脉搏波频域特征分类结果 Tab 9 Frequency domain feature classification results of pulse wave based on different attention mechanism combination models  n＝5,x±s Combined method Attention Accuracy F1 score Precision Recall (a) TCNT+SE 0.906 2±0.032 3 0.871 8±0.039 5 0.921 5±0.015 2 0.883 1±0.022 1 TCNT+SK 0.931 3±0.008 3 0.912 0±0.011 6 0.934 6±0.008 8 0.912 2±0.007 9 TCNT+CBAM 0.929 2±0.022 2 0.904 6±0.026 0 0.936 1±0.022 2 0.908 2±0.040 6 TCNT+SimAM 0.910 4±0.019 3 0.880 5±0.021 6 0.924 6±0.012 4 0.889 5±0.019 5 TCNT+CA 0.914 6±0.032 5 0.880 8±0.036 7 0.928 1±0.026 9 0.886 3±0.035 4 (b) TCNT+SE 0.906 2±0.013 2 0.882 1±0.018 7 0.914 2±0.009 3 0.885 4±0.024 6 TCNT+SK 0.910 4±0.034 0 0.888 5±0.036 4 0.921 7±0.029 9 0.904 0±0.042 2 TCNT+CBAM 0.902 1±0.032 0 0.866 0±0.051 1 0.913 2±0.030 2 0.876 1±0.047 9 TCNT+SimAM 0.872 9±0.043 9 0.823 9±0.084 7 0.893 5±0.027 2 0.822 0±0.096 2 TCNT+CA 0.889 6±0.026 8 0.848 3±0.039 0 0.896 1±0.027 0 0.844 9±0.054 8 (c) TCNT+SE 0.920 8±0.015 6 0.893 0±0.020 7 0.940 5±0.013 2 0.920 0±0.019 4 TCNT+CBAM 0.918 7±0.019 1 0.885 0±0.028 5 0.923 0±0.020 6 0.881 5±0.040 7 TCNT+SimAM 0.918 7±0.029 0 0.890 1±0.034 2 0.932 3±0.021 6 0.909 4±0.024 5 TCNT+CA 0.916 7±0.017 4 0.884 7±0.021 6 0.931 9±0.012 7 0.901 0±0.019 1 TCNT: Temporal convolutional network Transformer; SE: Squeeze-and-excitation; SK: Selective kernel; CBAM: Convolutional block attention module; SimAM: A simple parameter-free attention module; CA: Coordinate attention.

表 9 不同注意力机制融合模型的脉搏波频域特征分类结果 Tab 9 Frequency domain feature classification results of pulse wave based on different attention mechanism combination models

单独使用上述5个注意力机制模型所得到的分类实验结果见表 10。SE通过一个权重矩阵从通道域的角度赋予图像不同位置不同的权重，得到更重要的特征信息。CBAM可以在通道和空间维度上进行注意力的计算，保证了其能够作为即插即用的模块集成到现有的网络架构中。CA将通道注意力分解为2个一维特征编码过程，分别沿2个空间方向聚合特征，这样可以将其互补地应用于输入特征图，以增强关注对象的表示。SK在SE的基础上进行了改进，它对输入特征图中的不同大小物体自动选择对应的卷积核来提取特征，生成通道注意力信息。SimAM提出了优化能量函数以发掘每个神经元的重要性，且不会引入额外的参数。由表中数据可见，单独使用SimAM注意力机制得到的分类效果比单独使用SK更好，但是在本实验的融合模型实验中，SK与自注意力组合使用时模型的性能表现最佳，这是因为SK能使用不同尺寸的卷积核对输入的特征信息进行特征提取，然后自动选择合适的卷积核，更适合于训练本实验使用的脉搏波频域特征信息。

表 10 (Tab 10)

表 10 单独注意力机制模型的脉搏波频域特征分类结果 Tab 10 Frequency domain feature classification results of pulse wave based on attention mechanism models alone  n＝5,x±s Attention Accuracy F1 score Precision Recall SE 0.697 9±0.162 3 0.489 1±0.304 2 0.558 1±0.291 3 0.554 8±0.271 3 CBAM 0.797 9±0.075 9 0.691 4±0.128 1 0.793 7±0.092 7 0.697 3±0.118 8 CA 0.856 2±0.106 5 0.786 5±0.174 3 0.896 1±0.062 0 0.800 0±0.177 2 SK 0.904 2±0.024 1 0.875 5±0.032 4 0.907 6±0.026 0 0.874 8±0.040 1 SimAM 0.914 6±0.021 2 0.880 3±0.024 5 0.922 9±0.016 9 0.890 6±0.011 0 SE: Squeeze-and-excitation; CBAM: Convolutional block attention module; CA: Coordinate attention; SK: Selective kernel; SimAM: A simple parameter-free attention module.

表 10 单独注意力机制模型的脉搏波频域特征分类结果 Tab 10 Frequency domain feature classification results of pulse wave based on attention mechanism models alone

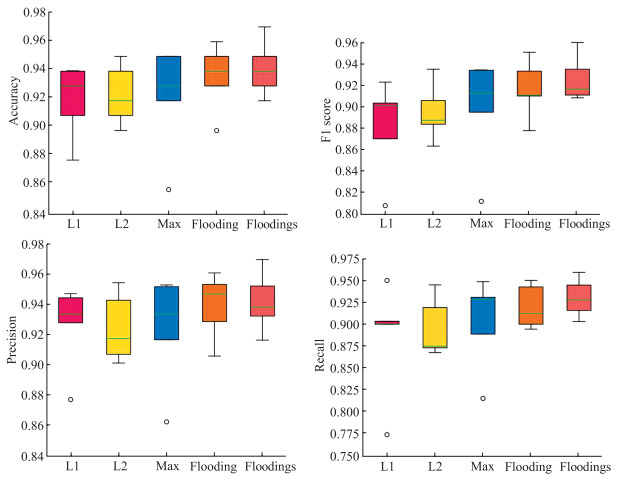
在TCNT-SK模型使用融合策略(a)的基础上，选择不同正则化方法时融合模型的分类结果见表 11，模型性能的5折交叉验证结果见图 5，分析数据可知常见的3种正则化手段没能改善模型性能，因为L1、L2是通过添加惩罚项来限制模型参数的取值范围，从而减少过拟合的风险。然而，如果过度限制模型参数的取值范围可能会导致模型无法很好地适应训练数据，从而影响模型的准确度。Max是一种基于约束的正则化方法，它通过限制参数向量的范数来控制模型的复杂度，因此可能会阻止模型使用某些参数组合来拟合数据，导致模型性能降低。而Floodings策略通过引入额外的约束假设，间接控制训练损失值的下降，能够提高模型的鲁棒性和泛化性。本实验结果显示，引入Floodings策略的融合模型TCNT-SK(Fs)的准确度为0.939 6，F1值为0.924 9，精确率为0.940 9，召回率为0.929 5，相较于未加入正则化的TCNT-SK模型，其在准确度上提高了0.89%，F1值提升了1.41%，精确率提升了0.67%，召回率提升了1.90%。

表 11 (Tab 11)

表 11 选择不同正则化方法的TCNT-SK模型的脉搏波频域特征分类结果 Tab 11 Frequency domain feature classification results of TCNT-SK model with different regularization methods  n＝5,x±s Regularization Accuracy F1 score Precision Recall L1 0.916 7±0.023 8 0.879 8±0.040 4 0.925 2±0.025 4 0.884 6±0.059 4 L2 0.920 8±0.019 3 0.893 8±0.024 1 0.923 8±0.020 6 0.895 1±0.030 9 Max 0.918 7±0.034 5 0.896 3±0.045 4 0.922 7±0.033 3 0.901 6±0.048 1 Flooding 0.933 3±0.021 4 0.915 3±0.024 7 0.938 3±0.019 7 0.919 2±0.022 6 Floodings 0.939 6±0.017 9 0.924 9±0.019 4 0.940 9±0.018 0 0.929 5±0.020 1 TCNT: Temporal convolutional network Transformer; SK: Selective kernel.

表 11 选择不同正则化方法的TCNT-SK模型的脉搏波频域特征分类结果 Tab 11 Frequency domain feature classification results of TCNT-SK model with different regularization methods

图 5 选择不同正则化方法的TCNT-SK模型性能的5折交叉验证结果箱线图 Fig 5 Boxplot of 5-fold cross-verification results of TCNT-SK model with different regularization methods n＝5. TCNT: Temporal convolutional network Transformer; SK: Selective kernel.

不使用正则化、使用Flooding策略和使用Floodings策略3种情况下模型训练过程的损失值下降过程见图 6，可以看出直观正则化手段对模型性能的影响。Floodings策略通过设置损失值的下限，阻止了损失值的过快下降，模型训练过程更加平滑，最终得到的解也更接近全局最优解。

图 6 模型训练过程中损失值的下降 Fig 6 Decrease of loss values during model training A: Without using regularization; B: Flooding; C: Floodings.

为了验证融合模型TCNT-SK(Fs)的分类效果，本实验对比了TCNT-SK(Fs)模型与长短时记忆（long short-term memory，LSTM）、CNN-LSTM、双边残差网络（bi-residual network，BRNet）、多尺度残差网络（multi-scale residual network，MIRNet）和密集连接卷积网络（dense convolutional network，DenseNet）5种典型时间序列分类模型及随机森林（random forest）和梯度提升决策树（extreme gradient boosting，XGBT）2种机器学习模型的分类评价指标，结果见表 12；使用5折交叉验证得到的每一折对应的损失曲线、ROC曲线和PR曲线见图 7。机器学习模型随机森林和XGBT难以学习到脉搏波频域特征的深层次关联，模型精度偏低。典型时间序列分类模型LSTM模型的准确度为0.900 0，F1值为0.878 9，精确率为0.911 7，召回率为0.903 3，具有较好的泛化性；而CNN-LSTM增加了CNN卷积层后表现更好，这是因为卷积层可以提取具有局部关联关系的脉诊特征，提高了模型分类速度和准确度；BRNet虽然采用了ResNet基本架构，但准确度比TCNT-SK(Fs)低了4.64%，这是因为脉搏波的频域特征是深层特征，BRNet模型的深度较浅，无法学习到所有的脉搏波特征信息；MIRNet模型在ResNet模块的基础上加入了Inception模块，模型深度较深，准确度比TCNT-SK(Fs)低了4.40%，但模型结构复杂，训练所需的资源与时间成本较高；DenseNet的思路与ResNet一致，但是它建立的是前面所有层与后面层的密集连接，通过特征在通道维度Channel上的连接来实现特征重用，使得DenseNet在参数和计算成本更少的情形下实现比ResNet更优的性能，但相较于TCNT-SK(Fs)模型其准确度低了2.66%，F1值低了5.43%。与LSTM、BRNet、MIRNet、DenseNet模型相比，本实验的TCNT-SK(Fs)模型的AUC值分别增加了4.81%、5.33%、2.43%、5.78%，因此，对于高血压患者危险分层数据，TCNT-SK(Fs)模型可以提取关联性较强的深层特征，具有较高的分类精度和较好的泛化性能。

表 12 (Tab 12)

表 12 不同模型对高血压患者危险分层的评价指标 Tab 12 Evaluation indicators of different models for risk stratification of hypertension patients n＝5,x±s Model Accuracy F1 score Precision Recall AUC RF 0.544 5±0.025 1 0.434 7±0.021 8 0.394 5±0.032 3 0.328 4±0.020 6 0.691 7±0.016 1 XGBT 0.565 4±0.008 0 0.428 0±0.006 3 0.430 9±0.089 1 0.332 8±0.008 8 0.709 5±0.010 6 LSTM 0.900 0±0.032 0 0.878 9±0.039 5 0.911 7±0.028 6 0.903 3±0.039 9 0.947 8±0.041 9 CNN-LSTM 0.918 7±0.034 5 0.901 2±0.035 8 0.927 4±0.029 5 0.904 1±0.029 3 0.918 1±0.038 0 BRNet 0.897 9±0.036 3 0.865 9±0.044 8 0.910 9±0.023 5 0.879 3±0.032 6 0.943 1±0.048 4 MIRNet 0.900 0±0.029 5 0.872 1±0.029 9 0.932 1±0.014 4 0.904 8±0.021 3 0.969 8±0.035 0 DenseNet 0.914 6±0.043 4 0.874 7±0.106 9 0.932 7±0.023 2 0.892 4±0.097 8 0.939 1±0.056 4 TCNT-SK(Fs) 0.939 6±0.017 9 0.924 9±0.019 4 0.940 9±0.018 0 0.929 5±0.020 1 0.993 4±0.003 3 RF: Random forest; XGBT: Extreme gradient boosting; LSTM: Long short-term memory; CNN: Convolutional neural network; BRNet: Bi-residual network; MIRNet: Multi-scale residual network; DenseNet: Dense convolutional network; TCNT-SK(Fs): Temporal convolutional network Transformer-selective kernel (Floodings); AUC: Area under curve.

表 12 不同模型对高血压患者危险分层的评价指标 Tab 12 Evaluation indicators of different models for risk stratification of hypertension patients

图 7 不同模型5折交叉验证的损失（A、D、G、J、M）、ROC（B、E、H、K、N）和PR（C、F、I、L、O）曲线 Fig 7 Loss (A, D, G, J, M), ROC (B, E, H, K, N) and PR (C, F, I, L, O) curves of 5-fold cross-verification of different models A-C: 0-fold cross-validation; D-F: 1-fold cross-validation; G-I: 2-fold cross-validation; J-L: 3-fold cross-validation; M-O: 4-fold cross-validation. ROC: Receiver operating characteristic; PR: Precision-recall; LSTM: Long short-term memory; CNN: Convolutional neural network; BRNet: Bi-residual network; MIRNet: Multi-scale residual network; DenseNet: Dense convolutional network; TCNT-SK(Fs): Temporal convolutional network Transformer-selective kernel (Floodings); RF: Random forest; XGBT: Extreme gradient boosting; AUC: Area under curve; AP: Average precision.

不同模型训练完整的5折交叉验证的模型参数量（parameter）、计算量（floating point operations）和运行时间（running time）见表 13。机器学习模型随机森林和XGBT模型简单，运行较快，但性能表现一般。LSTM模型运行时间较短，参数量适中，在增加CNN卷积层后，由于CNN具有特征提取和降维作用，减少了LSTM的参数量和运行时间，改善了模型性能。BRNet网络相对简单，运行时间较短。而MIRNet和DenseNet网络深度较深，模型复杂度高，参数量、计算量和运行时间都大大增加，模型综合性能一般。TCNT-SK(Fs)模型在5折交叉验证中的模型复杂度下，获得了较好的性能表现，是权衡资源与性能后的更优选择。

表 13 (Tab 13)

表 13 不同模型的参数量、FLOP和运行时间 Tab 13 Parameters, FLOP, and running time of different models Model Parameter/byte FLOP (×109) Running time/s RF 6.6 XGBT 35.9 LSTM 97 107 0.072 55.6 CNN-LSTM 60 423 0.077 41.4 BRNet 86 473 0.008 45.0 MIRNet 8 088 418 29.222 4 821.2 DenseNet 9 841 859 12.590 1 198.6 TCNT-SK(Fs) 526 414 0.542 346.6 RF: Random forest; XGBT: Extreme gradient boosting; LSTM: Long short-term memory; CNN: Convolutional neural network; BRNet: Bi-residual network; MIRNet: Multi-scale residual network; DenseNet: Dense convolutional network; TCNT-SK(Fs): Temporal convolutional network Transformer-selective kernel (Floodings); FLOP: Floating point operation.

表 13 不同模型的参数量、FLOP和运行时间 Tab 13 Parameters, FLOP, and running time of different models

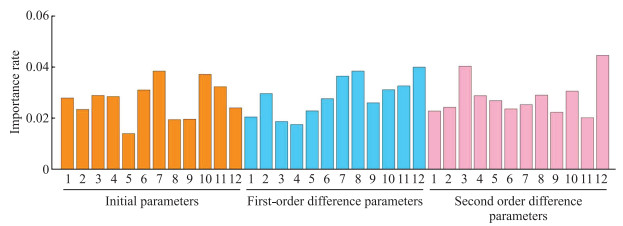
特征贡献率是衡量每个输入特征对模型预测结果影响的指标。贡献率越大，特征越重要，对分类结果的影响也就越大。本实验采用XGBT算法分析36个脉搏波频域MFCC特征，计算出各特征的贡献率，并绘制可视化图（图 8）。其中二阶差分的S3和S12两个特征贡献率均超过了4%，但总体来看，脉搏波的静态特征、一阶差分和二阶差分系数的贡献率相对均衡，各个特征对分类结果都具有重要的影响，说明高血压危险程度不仅与脉搏波的静态特征相关，也应当考虑脉搏波的动态特征。因此，应积极寻找脉搏波静态与动态特性的物理意义，并在临床实践中加以应用，将有助于更准确地诊断和治疗。

图 8 基于XGBT算法的36个脉搏波频域MFCC特征贡献率 Fig 8 Contribution rates of 36 MFCC features in the frequency domain of pulse waves based on XGBT algorithm XGBT: Extreme gradient boosting; MFCC: Mel-scale frequency cepstral coefficient.

本研究提出了一种使用深度学习融合模型对中医学脉搏波信号进行分析，从而实现对高血压患者进行危险分层的方法。该模型采用不同注意力机制决策融合方法，可以有效地提取脉诊数据频域特征的深层次关联，具有较高的分类性能。通过实验验证，与典型分类模型相比，该模型具有较高的分类精度和泛化性能，准确度为0.939 6，F1值为0.924 9，精确率为0.940 9，召回率为0.929 5，AUC值为0.993 4。该模型为中医脉诊对高血压患者进行风险分层研究提供了一种有效方法，为高血压层级诊断提供了新思路。