2. 海军军医大学(第二军医大学)海军卫勤训练基地,上海 200433
2. Naval Medical Service Training Base, Naval Medical University (Second Military Medical University), Shanghai 200433, China
传染病不仅严重威胁军队成员的生命安全,而且严重阻碍部队战斗力的生成。我军一直坚持“预防为主”的卫生方针,建立、健全了各级卫生防疫机构,强化了对传染病的管理机制。但在2003年应对严重急性呼吸综合征(severe acute respiratory syndrome,SARS)和2019年至今抗击新型冠状病毒肺炎(coronavirus disease 2019,COVID-19)疫情的过程中,我军的疫情防控工作仍面临巨大挑战。在面对已经出现或潜在发生的传染病时,负责卫生防疫工作的卫勤人员只有在短时间内做到对疫情发展态势的现况理解和初步预测,才能给出可行的应对方案。目前虽然我军已建立了集疫情信息采集、分析、预报和控制为一体的军队疾病预防控制机构,但针对特殊机动单元的任务执行群体,具有较高参考价值的预测模型仍十分缺乏。
海军大型战斗舰艇作为一种重要的海上作战平台,内部空间紧凑,编制人员密集,一旦发生传染病极易流行。在执行出海任务的过程中,除了靠码头补给和靠帮补给,舰艇人员内外的流动几乎是停滞的,这种封闭的环境导致舰艇本身承载的舰员和官兵群体天然地构成了典型的传染病仓室模型结构。也就是说,舰上人员可被划分为若干个类别(仓室),每个人都必然处于一种疾病状态(如潜伏状态、感染状态、易感状态等),海军大型战斗舰艇上发生传染病的场景非常适合通过数学手段建立仓室模型,以便相关卫勤人员更好地研究传染病的传播动力学过程。
1 经典的传染病预测模型 1.1 马尔萨斯(Malthus)模型/S模型马尔萨斯模型是由英国人口和统计学家托马斯·罗伯特·马尔萨斯(Thomas Robert Malthus)牧师于1798年提出的一种人口数学模型[1]
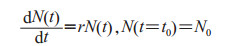
|
(1) |
其中,r代表出生率,假定为常数,或称为生命系数;N(t)为t时刻的人口数量。
可得式(1)的解为

|
(2) |
如果r>0,则人口增长将会按照指数规律无限增长。若将t以1年或10年为单位离散化,则人口总数按以er为公比的等比数列增加。这就是马尔萨斯人口指数增长模型,简称马尔萨斯模型。在用于传染病建模时,因该模型只有单一的易感人群变量,故有学者称其为S模型[2]。
当人口数量不大时,生存空间和资源非常充裕,人口总数确实可能呈现指数增长,此时上述模型能够很好地说明人口总数的增长情况。但当人口总数很大时,指数增长的线性模型无法反映出环境条件的限制,也无法给出在受到这一限制时可供养人数的上限值。
在将该模型用于模拟传染病的流行时,可以假设在外执行任务的某舰艇总人数为n,初始时刻t0共有i0人感染疾病,t时刻感染的人数为i(t)。假设每例感染者在单位时间内都会将疾病传染给k人,且此病患者既没有死亡也不会康复,则有与式(1)相同的模型,并得到式(2)的解。式中假设为常数的r在医学上可被称为该传染病在此舰艇环境中的传染强度。
同理可知,在舰艇总人数较少的情况下,马尔萨斯模型可被用于预测流行初期的感染人数,但随着时间的推移,它将越来越偏离实际情况。
1.2 逻辑斯蒂(logistic)模型/SI模型在马尔萨斯模型的式(2)中,模型以er为公比呈几何级数无限增长,所以会脱离实际。很明显,对传染病流行而言,在现存健康总人数固定的情况下,感染者数量的无限增长是不可能的。1834年,比利时数学家皮埃尔·弗朗索瓦·韦胡斯特(Pierre Francois Verhulst)在马尔萨斯模型的基础上,提出了受限条件下的人口增长模型,之后他又引入了逻辑斯蒂增长模型、逻辑斯蒂方程等重要概念[3]。
为了避开马尔萨斯模型无限制的假设,韦胡斯特引入了环境最大容纳量常数Nm(也常用K表示),用于表示自然资源条件所能容纳的最大人口数,并假设其净相对增长率为r(1-N(t)/Nm)。也就是说,相对增长率随N(t)的增加而降低,而当N(t)→Nm时,净增长率→0。此时人口增长的方程变为

|
(3) |
这就是由韦胡斯特命名的经典逻辑斯蒂方程。其中r可称为内禀自然增长率(intrinsic rate of natural increase),即在空间、食物等资源无限制的条件下种群所能达到的最大增长率,这个常数反映了种群的内在特征。
设初值条件t=t0,N=N0,则式(3)的解为

|
(4) |
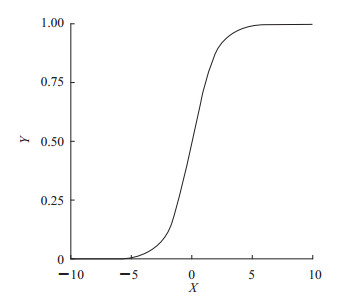
这就是著名的逻辑斯蒂模型。从示例模型图(图 1)可以看出,逻辑斯蒂曲线呈S形。
|
图 1 逻辑斯蒂曲线示例(环境最大容纳量常数Nm=1) |
当Nm与N相比非常大的时候,rN2/Nm与rN相比就非常小,此时即恢复到近似无限制的马尔萨斯模型;反之,则rN2/Nm的存在感越强,环境的限制就越能产生作用,人口总数的增长速度就会更快地下降。因此,逻辑斯蒂模型也称为增长阻滞模型。
逻辑斯蒂模型通常分为开始期、加速期、转折期、减速期和饱和期5个时期。在开始期,个体数量少,密度增长缓慢,也称为潜伏期;随着个体数量的增加,密度的增长加速,进入加速期;当个体数量达到饱和数量的一半时,密度增长速度升至顶峰,随后立刻下降,即转折期;在减速期,个体数量继续增加,但密度的增长速度变慢;在饱和期,个体数量达到了环境最大容纳量,无法继续增加。
用于传染病场景时,逻辑斯蒂模型可有效地区分易感者和感染者,因此也被称为SI模型。它是最简单的传染病模型,设定所有个体一旦感染就永远处于感染的状态。但即便是单纯模拟人口的变化,在实际社会中影响人口变化的因素也很多,如老龄化进程、性别比的变化、年龄结构等,这使得逻辑斯蒂模型仍存在诸多不完美之处。
在逻辑斯蒂模型的基础上,若假设已经康复的人并不能获得免疫力,则他们又成了易感人群,这就构成了易感-感染-易感(susceptible-infected-susceptible,SIS)模型。这种模型有一定的应用范围,但始终受逻辑斯蒂模型的人群状态限制,与实际情况存在差距。
1.3 易感-感染-恢复(susceptible-infected-recovered,SIR)模型苏格兰生物化学家威廉·奥格威·克马克(William Ogilvy Kermack)与流行病学家安德森·格雷·麦肯德里克(Anderson Gray McKendrick)在1927[4]、1932[5]和1933年[6]发表了一系列文章,共同提出了SIR模型。SIR模型引入了新的变量,更加适用于描述传染病发展的整体趋势,成为研究传染病动力学的经典模型。COVID-19疫情暴发以来,该动力学模型已被广泛应用于传染病流行规律的探索、传染病数学模型的构建及传染病预测和控制等工作中[7-10]。
在SIR模型中人群可分为3类:(1)易感人群/易感者,是在某时刻尚未感染疾病但存在感染风险的人群,数量记为S(t);(2)已感染人群/感染者,是在某时刻已经被感染且自身成为一类传染源的人群,数量记为I(t);(3)已痊愈人群/恢复者,是在某时刻已经得到合理治疗并康复的人群,数量记为R(t)。
若t时刻的总人数为N(t),则有
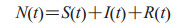
|
(5) |
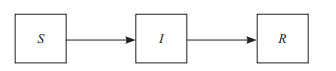
SIR模型的建立基于3个假设:(1)忽略动力学因素,人口数量始终保持恒定,即N(t)=K;(2)假定易感者在接触感染者后会被传染,在t时刻,易感者的数量与一例感染者能传染的易感者数量呈正相关,其比例系数为β,则被传染的人数为βS(t)I(t);(3)存在一个时刻t,此时恢复者与感染者数量成正比,其比例系数为γ,则单位时间内恢复者数量为R(t)=γI(t)。由此可以得到人群类别的发展过程(图 2)。
|
图 2 易感-感染-恢复模型结构 S:易感人群/易感者;I:已感染人群/感染者;R:已痊愈人群/恢复者. |
SIR模型的微分方程组为

|
(6) |
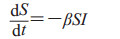
|
(7) |
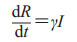
|
(8) |
由此可得,感染者的数量I=(S0+I0)-S+(1/σ)ln(S/S0),其中被感染者接触的人数为σ=β/γ。
以上即为最原始的SIR模型。
与基于逻辑斯蒂模型建立SIS模型一样,如果假设感染者即便痊愈仍然无法获得长久的免疫力,即令痊愈者在经过一段时间之后回归到易感人群,此时可以拓展出易感-感染-恢复-易感(susceptible-infected-recovered-susceptible,SIRS)模型。
海军舰艇在执行任务尤其是长远航任务的过程中,总人数是相对固定的;官兵的轮岗频率相对固定,且同时在1~2个餐厅就餐,在没有设隔离制度的情况下,其感染者接触率也较为稳定。因此,针对痊愈后可获得长期免疫的传染病人群,或虽无法获得长期免疫但仍处于免疫保护的发展阶段的恢复者,就可以采用基础的SIR模型进行预测。
SIR模型没有纳入对检疫工作的考虑。检疫是对曾与感染者或感染环境接触并有可能感染而成为传播者的人所采取的管理措施。作为卫生防疫工作的重要内容之一,检疫的目的是防止可能的潜在传播者在传染病的潜伏期向外传播疾病。SIR模型需要加入尚未发病的感染者,才能更加接近实际情况。
1.4 易感-暴露-感染-恢复(susceptible-exposed-infected-recovered,SEIR)模型SEIR模型是目前传染病研究最常用的模型,其被广泛运用的原因在于它可以清晰地描述传染病传播的动态逻辑关系,并在合适参数下能够给出相对准确的传播趋势预测。在COVID-19疫情发生后,已有许多应用该模型进行预测的研究[11-13]。
SEIR模型将人群分为4类,在SIR模型的3类人群之外增加了暴露者/潜伏者这一变量,数量记为E(t)。总人数N仍旧是所有类别人数之和,即N=S+E+I+R。健康人群的比例为S/N。
SEIR模型的微分方程为
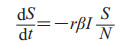
|
(9) |

|
(10) |
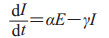
|
(11) |

|
(12) |
其中,r代表一例感染者接触的人数,β代表未感染者变成潜伏者的概率,γ代表感染者最终痊愈变成恢复者的概率,α代表潜伏者变成感染者的概率。由此得到该模型人群类别的发展过程(图 3)。

|
图 3 易感-暴露-感染-恢复模型结构 S:易感人群/易感者;E:暴露者/潜伏者;I:已感染人群/感染者;R:已痊愈人群/恢复者;β:S变成E的概率;α:E变成I的概率;γ:I最终痊愈变成R的概率. |
虽然SEIR模型引入了潜伏者这一变量,大大增强了与现实生活的相似性,但对COVID-19这类包含无症状感染者的传染病,传统的SEIR模型仍然需要改进,以满足更加复杂的现实应用需求。例如,有的模型增加了无症状感染者和病死者这2个新的变量,构建易感-暴露-感染-无症状感染-病死-恢复(susceptible-exposed-infected-asymptomatic-dead-recovered,SEIADR)模型来实施疫情预测[12];也有学者采用自适应权重的粒子群(particle swarm optimization,PSO)算法对SEIR模型进行反演计算,构建了PSO-SEIR模型[14]。
2 仓室模型以上4种经典模型都将总体人群分成了不同的虚拟仓室,传染病的传播就好像是使人们从一个仓室“进入”另一个仓室,因此都是典型的仓室模型。其基本思路是将人群划分为若干个类别(仓室),用来代表处于不同疾病状态的人群,然后采用数学手段建立这些变量的动力学方程,研究传染病的传播动力学过程[15]。严格地讲,仓室模型概念的提出源于经典SIR模型。
SIR模型是最常见、最简单的仓室模型,大部分复杂模型都源于SIR模型。该模型更适于模拟人传人的疾病,如麻疹、风疹和流行性腮腺炎等。在经典模型的基础上,学者们建立了种类丰富的模型库,可根据不同的舰艇类型、不同的预测时长、不同的传播阶段、不同的危险程度进行模型选择。
仓室模型通常用常微分方程构建,是确定性的,也有随机性的框架,且随机性本身可以让模型更加贴近复杂的现实情况。
为了理清各类仓室模型的适用范围,本文总结了各类仓室模型及其关键特征(表 1),以期能帮助相关卫勤人员选择适合海军舰艇环境及其任务场景的传染病预测模型,更好地应对COVID-19疫情等卫生防疫工作中的挑战。
|
|
表 1 传染病仓室模型类型及关键特征描述 |
3 实际模拟需求和模型选择
对基础模型的选择,必须综合考虑海军大型战斗舰艇的舰船特征、任务属性、人员组成等因素。除了舰艇相关因素,所要模拟的疫情发展阶段及传染病本身具备的传播特征也应予以重视。针对海军大型战斗舰艇常见的实际模拟需求,以下几种模型更可能被选用。
(1)针对海军大型战斗舰艇已经出现或可能存在潜在“零号病人”的情景进行建模,仅需使用马尔萨斯模型或逻辑斯蒂模型即可。“零号病人”指第1个感染并开始散播病原体的患者,在流行病调查中常被称为初始病例或标识病例,对“零号病人”的细致调查可为病因分析、预测、控制措施的选择、预警机制的建立提供宝贵信息。如果舰艇获知自身满足潜在暴露条件(如物资补给、人员轮换等)的时间是在暴露完成之后,且潜在“零号病人”的检疫工作并未立即执行,相关卫勤人员应当立刻建立初期无资源限制的病例增长模型。此时建立预测模型的实际作用主要是尽快明确舰艇自持能力受疫情影响的最大程度,从而做好充足的卫勤管理准备。
(2)如果检疫工作已顺利开展,传染病在海军大型战斗舰艇环境中传播的关键因素就是传播接触数量和频率,此时应当选用基础SEIR模型。式(9)、(10)中的r代表了一例感染者接触的人数,在检疫不出差错的情况下应当是0。一旦检疫工作不到位,r就会随着人员的流动模式迅速发生变化。例如,若检疫目标进入战位,则该战位轮值频率和人数进入模型,成为重要参数;若检疫目标进入餐厅,则就餐规模和就餐时长成为关键影响因素。此时建立预测模型的作用,是利用预测结果为检疫工作失效或低效情况下应急方案的制定提供核心参数,重点在于补救,而非计划。
(3)如果长远航任务时间较长,疫情传播已经越过了初期阶段,而在舰艇环境中病原体的迭代受限,则纳入了接种工作的易感-感染-恢复-接种(susceptible-infected-recovered-vaccinated,SIRV)模型或允许痊愈者返回易感人群的易感-暴露-感染-恢复-易感(susceptible-exposed-infected-recovered-susceptible,SEIRS)模型将会是更好的选择。在面对疫情防控的持久战时,病例清零任务的优先度将让位于战斗力的维护和保持。以COVID-19为例,在病原体迭代的时间框架下,任务时间极有可能已经相对地拉长到了某种程度,使舰艇环境微缩成人与病原体长期共存的小世界。模型中的时间跨度可被灵活控制和调整,而此时建模预测的目标就是通过模拟各类现实的干预方法,选出可令疫情起伏程度降至最低的卫生防疫措施。
综上所述,梳理和分析各类传染病模型十分有必要。海军大型战斗舰艇在执行任务尤其是长远航任务的过程中会面临诸多与其他军兵种截然不同的卫勤保障难题,一旦遭遇重大疫情,卫勤指挥和计划工作常常因缺少定量研究途径、没有定量结果支撑等现实困难而受到阻碍,严重影响卫生防疫、药材补给等后续工作的开展。卫勤人员可通过充分利用灵活多样的模拟平台和应用程序得到更好的数据支持,从而在相关卫勤工作中实施覆盖面更广的措施、制定针对性更强的方案、做出准确度更高的决策。
| [1] |
MEIRING H J. Thomas Robert Malthus, naturalist of the mind[J]. Ann Sci, 2020, 77: 495-523. DOI:10.1080/00033790.2020.1823479 |
| [2] |
马知恩, 周义仓, 王稳地, 靳祯. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004: 30-31.
|
| [3] |
CRAMER J S. The origins of logistic regression[R/OL]//Tinbergen Institute discussion paper. TI 2002-119/4. (2002-11)[2021-08-12]. https://papers.tinbergen.nl/02119.pdf.
|
| [4] |
KERMACK W O, MCKENDRICK A G. A contribution to the mathematical theory of epidemics[J]. Proc Royal Soc A Math Phys Eng Sci, 1927, 115: 700-721. |
| [5] |
KERMACK W O, MCKENDRICK A G. Contributions to the mathematical theory of epidemics.Ⅱ. The problem of endemicity[J]. Proc Royal Soc Lond, 1932, 138: 55-83. |
| [6] |
KERMACK W O, MCKENDRICK A G. Contributions to the mathematical theory of epidemics. Ⅲ. Further studies of the problem of endemicity[J]. Proc Royal Soc Lond, 1933, 141: 94-122. |
| [7] |
朱仁杰, 唐仕浩, 刘彤彤, 郭燕, 董珊珊, 成瀛, 等. 基于改进SIR模型的新型冠状病毒肺炎疫情预测及防控对疫情发展的影响[J]. 陕西师范大学学报(自然科学版), 2020, 48: 33-38. DOI:10.15983/j.cnki.jsnu.2020.03.018 |
| [8] |
郭云龙. 基于SIR模型的机动车内传染病传播研究[J]. 中国安全科学学报, 2021, 31: 173-178. DOI:10.16265/j.cnki.issn1003-3033.2021.01.025 |
| [9] |
李承倬, 武文韬, 潘振宇, 邓玉皎, 李筱, 代志军, 等. 基于SIR模型和基本再生数的浙江省新型冠状病毒肺炎防控效果分析[J]. 浙江医学, 2020, 42: 311-314. |
| [10] |
张艳霞, 李进. 基于SIR模型的新冠肺炎疫情传播预测分析[J]. 安徽工业大学学报(自然科学版), 2020, 37: 94-101. DOI:10.3969/j.issn.1671-7872.2020.01.015 |
| [11] |
冯苗胜, 王连生, 林文水. Logistic与SEIR结合模型预测新型冠状病毒肺炎传播规律[J]. 厦门大学学报(自然科学版), 2020, 59: 1041-1046. |
| [12] |
王国柱, 池晓航, 周强. 基于改进SEIR模型的疫情预测与分析[J]. 河南工学院学报, 2020, 28: 29-33. DOI:10.3969/j.issn.1008-2093.2020.05.007 |
| [13] |
王思远, 谭瀚霖, 李东杰. 基于改进传染病动力学易感-暴露-感染-恢复(SEIR)模型预测新型冠状病毒肺炎疫情[J]. 第二军医大学学报, 2020, 41: 637-641. WANG S Y, TAN H L, LI D J. Coronavirus disease 2019 epidemic trend prediction based on improved infectious disease dynamics susceptible-exposed-infected-recovered (SEIR) model[J]. Acad J Sec Mil Med Univ, 2020, 41: 637-641. |
| [14] |
罗丹婷, 钱华, 刘聪, 黄顺祥. 不同国家和时段COVID-19控制策略效果评价: 基于自适应PSO-SEIR模型[J]. 科学通报, 2021, 66: 453-464. |
| [15] |
王俊芬, 陈振煜, 刘思德. 基于仓室模型的传染病动力学建模方法概述及应用[J]. 现代消化及介入诊疗, 2020, 25: 280-283. |
| [16] |
BANASIAK J, PHONGI E K, LACHOWICZ M. A singularly perturbed SIS model with age structure[J]. Math Biosci Eng, 2013, 10: 499-521. DOI:10.3934/mbe.2013.10.499 |
| [17] |
HOSHI K, KASAHARA H, MAKIOKA R, SUZUKI M, TANAKA S. Trade-off between job losses and the spread of COVID-19 in Japan[J]. Jpn Econ Rev (Oxf), 2021, 72: 683-716. DOI:10.1007/s42973-021-00092-w |
| [18] |
MOUANGUISSA L N, KAMARA A A, WANG X J. Modeling 2018 Ebola virus disease outbreak with Cholesky decomposition[J]. Math Methods Appl Sci, 2021, 44: 5739-5752. DOI:10.1002/mma.7145 |
| [19] |
YANG J X. A SIRD epidemic model with community structure[J/OL]. Chaos, 2021, 31: 013102. DOI: 10.1063/5.0019995.
|
| [20] |
曾志坚, 吴汪洋. 贸易渠道视角下的金融危机传染研究: 基于复杂网络与SIRS模型[J]. 湖南大学学报(社会科学版), 2018, 32: 87-93. |
| [21] |
王刚, 冯云, 陆世伟, 马润年. 多操作系统异构网络的病毒传播模型和安全性能优化策略[J]. 电子与信息学报, 2020, 42: 972-980. |
| [22] |
HUNTINGFORD C, RAWSON T, BONSALL M B. Optimal COVID-19 vaccine sharing between two nations that also have extensive travel exchanges[J/OL]. Front Public Health, 2021, 9: 633144. DOI: 10.3389/fpubh.2021.633144.
|
| [23] |
GOULET A, BLANGY S, REDDER P, PRANGISHVILI D, FELISBERTO-RODRIGUES C, FORTERRE P, et al. Acidianus filamentous virus 1 coat proteins display a helical fold spanning the filamentous archaeal viruses lineage[J]. Proc Natl Acad Sci USA, 2009, 106: 21155-21160. |
| [24] |
RIFHAT R, TENG Z D, WANG C X. Extinction and persistence of a stochastic SIRV epidemic model with nonlinear incidence rate[J/OL]. Adv Differ Equ, 2021, 2021: 200. DOI: 10.1186/s13662-021-03347-3.
|
| [25] |
PHAIJOO G R, GURUNG D B. Sensitivity analysis of SEIR-SEI model of dengue disease[J]. GAMS J Math Math Biosci, 2018, 6: 41-50. |
| [26] |
LUNELLI A. An SEI model for sarcoptic mange among chamois[J]. J Biol Dyn, 2010, 4: 140-157. |
| [27] |
陈友进. 一类SEIS流行病模型的全局动力学分析[J]. 常州信息职业技术学院学报, 2004, 3: 9-12. |
| [28] |
FOXALL E. The SEIS model, or, the contact process with a latent stage[J]. J Appl Prob, 2016, 53: 783-801. |
| [29] |
SIDE S, MULBAR U, SIDJARA S, SANUSI W. A SEIR model for transmission of tuberculosis[C]//The 4th International Conference On Mathematical Sciences. Putrajaya, Malaysia, 2017.
|
| [30] |
ZHOU M M, ZHANG T S. Global analysis of an SEIR epidemic model with infectious force under intervention strategies[J]. J Appl Math Phys, 2019, 7: 1706-1717. |
| [31] |
黄梦瑶, 黄丽达, 袁宏永, 刘罡. 社交隔离对COVID-19的发展影响[J]. 清华大学学报(自然科学版), 2021, 61: 96-103. |
| [32] |
魏泽萍, 刘贤宁. 一类具有潜伏时滞和非线性疾病发生率的SEIRS传染病模型[J]. 生物数学学报, 2019, 34: 63-74. |
| [33] |
MOHAMED I A, AISSA A B, HUSSEIN L F, TALOBA A I, KALLEL T. A new model for epidemic prediction: COVID-19 in Kingdom Saudi Arabia case study[J/OL]. Mater Today Proc, 2021. DOI: 10.1016/j.matpr.2021.01.088.
|
| [34] |
MCDONALD S A, MANGEN M J J, SUIJKERBUIJK A, COLZANI E, KRETZSCHMAR M E E. Effects of an ageing population and the replacement of immune birth cohorts on the burden of hepatitis A in the Netherlands[J/OL]. BMC Infect Dis, 2013, 13: 120. DOI: 10.1186/1471-2334-13-120.
|
| [35] |
ALMEIDA R, BRITO DA CRUZ A M C, MARTINS N, MONTEIRO M T T. An epidemiological MSEIR model described by the Caputo fractional derivative[J]. Int J Dyn Control, 2019, 7: 776-784. |
| [36] |
李学志, 万志超, 陈清江. 总人口规模变化的年龄结构MSEIR流行病模型的再生数[J]. 数学的实践与认识, 2005, 35: 113-122. |
| [37] |
陈清江, 蔡礼明, 代丽霞. 带接种疫苗的年龄结构MSEIR流行病模型非负解的存在惟一性[J]. 信阳师范学院学报(自然科学版), 2003, 16: 389-393. |
| [38] |
BADEJI-AJISAFE B. MSEIRS model for pediatrics with lower respiratory tract infection[J]. Glob J Med Res, 2018, 18: 11-13. |
| [39] |
EDWARD S. A Deterministic mathematical model for direct and indirect transmission dynamics of typhoid fever[J/OL]. Open Access Lib J, 2017, 4: e3493. DOI: 10.4236/oblib.1103493.
|
 2022, Vol. 43
2022, Vol. 43


