第二军医大学学报  2020, Vol. 41 Issue (6): 637-641   PDF    
引用本文
王思远, 谭瀚霖, 李东杰. 基于改进传染病动力学易感-暴露-感染-恢复(SEIR)模型预测新型冠状病毒肺炎疫情[J]. 第二军医大学学报, 2020, 41(6): 637-641  
WANG Si-yuan, TAN Han-lin, LI Dong-jie. Coronavirus disease 2019 epidemic trend prediction based on improved infectious disease dynamics susceptible-exposed-infected-recovered (SEIR) model[J]. Academic Journal of Second Military Medical University, 2020, 41(6): 637-641 (in Chinese with English abstract)  
基于改进传染病动力学易感-暴露-感染-恢复(SEIR)模型预测新型冠状病毒肺炎疫情
王思远1,2, 谭瀚霖3, 李东杰1     
1. 中南大学湘雅医院国际医疗部外科, 国家老年疾病临床研究中心, 长沙 410008;
2. 长沙矿冶研究院有限责任公司, 长沙 410000;
3. 国防科技大学系统工程学院, 长沙 410012
收稿日期: 2020-03-07    接受日期: 2020-04-01
基金项目: 国家自然科学基金(21806186)，国家科技部科研院所技术开发研究专项(2012EG113170).
作者简介: 王思远, 硕士生, 助理工程师.E-mail:774326377@qq.com.
通信作者(Corresponding author): 李东杰.Tel:0731-89753054, E-mail:dongjieli@csu.edu.cn.
摘要: 目的 研究基于传染病动力学易感-暴露-感染-恢复(SEIR)模型对新型冠状病毒肺炎(COVID-19)疫情发展情况的预测效果，为有效应对疫情提供指导。方法 利用Python爬虫自动更新功能获取中华人民共和国国家卫生健康委员会公布的疫情数据，通过改进传染病动力学SEIR模型，自动修正COVID-19基本再生数(R0)，对中国湖北省和韩国的COVID-19疫情发展趋势进行预测。结果 模型预测的湖北省COVID-19疫情顶点在2020年2月21日，现有确诊病例数约为50 000例(2月19日)，预计疫情将于3月4日回落至30 000例以下，并在5月10日左右结束。中华人民共和国国家卫生健康委员会公布的实际数据显示，确诊人数顶点为53 371例。模型预测的韩国疫情峰值在3月7日，将于4月底结束。结论 改进的传染病动力学SEIR模型在COVID-19疫情早期实现了较准确的数据预测，政府相关部门在疫情中及时、有效的强力干预明显影响了疫情的发展进程，东亚其他国家如韩国的疫情在3月仍处于上升期，提示中国需要提防输入性疫情风险。
关键词: 新型冠状病毒肺炎    传染病动力学    疫情数据    易感-暴露-感染-恢复模型    
Coronavirus disease 2019 epidemic trend prediction based on improved infectious disease dynamics susceptible-exposed-infected-recovered (SEIR) model
WANG Si-yuan1,2, TAN Han-lin3, LI Dong-jie1     
1. Xiangya International Medical Center, National Clinical Research Center for Geriatric Disorders, Xiangya Hospital, Central South University, Changsha 410008, Hunan, China;
2. Changsha Research Institute of Mining and Metallurgy Co., Ltd, Changsha 410000, Hunan, China;
3. School of System Engineer, National University of Defense Technology, Changsha 410012, Hunan, China
Supported by National Natural Science Foundation of China (21806186) and Technology Development Research Initiative Program of National Ministry of Science and Technology Research Institutes (2012EG113170).
Abstract: Objective To predict the coronavirus disease 2019 (COVID-19) epidemic situation based on the infectious disease dynamics susceptible-exposed-infected-recovered (SEIR) model, so as to provide guidance for effective control of the epidemic. Methods Python crawler automatic update function was used to collect the epidemic data released by the National Health Commission of China. An improved infectious disease dynamics SEIR model, which can automatically correct the COVID-19 basic reproductive number (R0), was constructed to predict the development trend of COVID-19 epidemic in Hubei Province of China and South Korea. Results The peak of the COVID-19 epidemic in Hubei Province of China predicted by the model would appear on Feb. 21, 2020. The number of confirmed COVID-19 cases would be about 50 000 on Feb. 19 and would fall to below 30 000 on Mar. 4, and the epidemic would end on May 10. According to the actual data released by the National Health Commission of China, the peak number of confirmed COVID-19 patients was 53 371. The model predicted that an epidemic peak in South Korea would be on Mar. 7, and would end at the end of April. Conclusion This improved infectious disease dynamics SEIR model established in the early stage of COVID-19 epidemic has achieved relatively accurate prediction. The timely and effective intervention by relevant government departments has significantly affected the development of the epidemic. The epidemic situation in other countries in East Asia, such as South Korea, is still on the rise in March, suggesting that China needs to be on guard against the risk of imported epidemic.
Key words: coronavirus disease 2019    infectious disease dynamics    epidemic data    susceptible-exposed-infected-recovered model    

根据中华人民共和国国家卫生健康委员会发布的新型冠状病毒肺炎(coronavirus disease 2019, COVID-19)疫情最新情况[1], 截至2020年4月28日12时, 全国累计确诊84 367例, 累计死亡4 643例, 累计治愈78 664例。目前除了中国外全球其他国家已经出现COVID-19疫情流行趋势, 东亚主要国家的疫情同样受人关注。

在COVID-19疫情防控过程中, 前瞻性地预测确诊病例数、疑似病例数等数据对各部门采取防控措施及精准施策有重要意义。耿辉等[2]利用易感-暴露-感染-恢复(susceptible-exposed-infected-recovered, SEIR)模型预测现行措施下的严重急性呼吸综合征冠状病毒2(severe acute respiratory syndrome coronavirus 2, SARS-CoV-2)感染人群及COVID-19潜伏期人群将会呈现明显下降趋势, 但并没有对具体疫情数据进行预测。由于SEIR模型需要获得人群感染率及潜伏期感染率[3-4], 本研究利用Python爬虫自动更新功能获得全国最新疫情数据。在改进的传染病动力学SEIR模型中, 由于基本再生数R0这一流行病学参数自动修正, 如何体现政府干预措施的力度是一个难点。原始SEIR模型将政府干预措施隐含在模型的感染率参数中, 我们利用易感人数下降率等效替代了感染率降低以完善SEIR模型, 从而对全国疫情发展进程进行预测。数值实验表明本研究改进的SEIR模型较好地解释了2020年2月19日24时之前湖北省病例数据变化, 并给出了湖北省疫情顶点(现存确诊人数峰值)及现有确诊人数回落至40 000、30 000、20 000、10 000和疫情结束的具体时间, 为相关机构抗疫措施和复工复产工作的调整提供参考。韩国的疫情数据相对日本比较准确, 目前疫情处于顶峰期, 会在3月中旬开始下降。东亚各国的疫情预测情况也将为中国疫情防控提供参考。

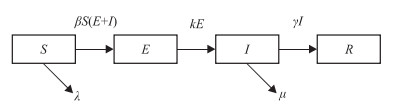
1 材料和方法 1.1 模型构建

建立一个改进的传染病动力学SEIR模型用于预测湖北省COVID-19疫情发展趋势。设定地区总人口数为N, 易感人数为S, 患病潜伏期人数为E, 现有确诊人数为I, 治愈人数为R, 4种人群之间的动力学模型见图 1。其中易感人群到患病潜伏期人群的转化率为β, 患病潜伏期人群到现有确诊人群的转化率为k, 现有确诊人群到治愈人群的转化率为γ。与现有其他SEIR模型不同的是, 本研究通过易感人群减少率λ建模政府管控措施, 较好地模拟了政府干预措施逐渐增强的现象。

图 1 预测湖北省COVID-19疫情发展趋势的传染病动力学SEIR模型 Fig 1 Infectious disease dynamics SEIR model of COVID-19 epidemic trend prediction in Hubei, China COVID-19: Coronavirus disease 2019; SEIR: Susceptible-exposed-infected-recovered; S: Susceptible population; E: Population during the incubation period; I: Existing confirmed population; R: Cured population; β: The conversion rate of susceptible population to population during the incubation period; k: The conversion rate of population during the incubation period to confirmed population; γ: The conversion rate of confirmed population to cured population; λ: The loss rate of susceptible population; μ: Mortality rate

该模型还考虑了患病人群的死亡情况, 设死亡人数为D, 病死率为μ, 图 1所示SEIR模型可以写成常微分方程组形式：

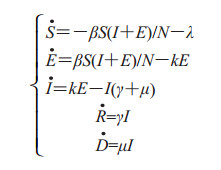
(1)
1.2 模型求解

SEIR模型的求解, 使用截至2020年2月19日24时中华人民共和国国家卫生健康委员会公布的湖北省每天累计确诊病例数、累计治愈病例数Rt和累计死亡病例数Dt作为原始数据, 可计算得到每天现有确诊病例数It。以中华人民共和国国家卫生健康委员会发布的2020年1月19日数据[5]作为模型初值, 则有I0＝170、R0＝25、D0＝3, 患病潜伏期人数初值没有观测数据, 设定E0＝I0。可用模型推演出1月20日至2月19日的含参数预测现有确诊病例数I(t)、治愈病例数R(t)和死亡病例数D(t)。利用最小二乘法构建损失函数：

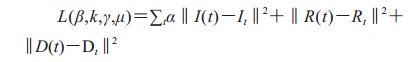
(2)

为了加强模型对现有确诊病例数的拟合, 损失函数中对现有确诊病例数的误差项进行了加权, 求解时取权重α＝5。

损失函数(2)是一个关于参数β、k、γ、μ的二次凸优化问题, 存在唯一最优解, 可用成熟的数值方法求解。本研究用Python软件求得参数β＝0.448、k＝0.045、γ＝0.015、λ＝2.289×106、μ＝0.003 9。

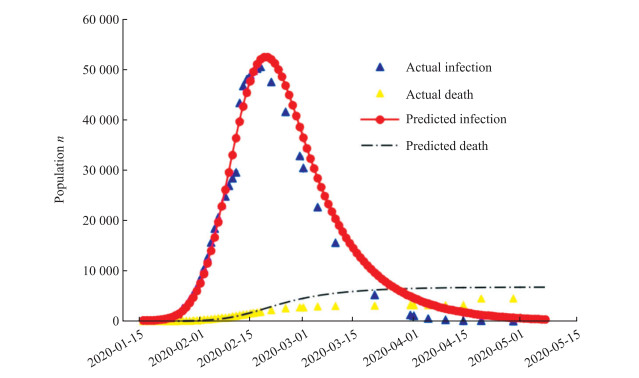
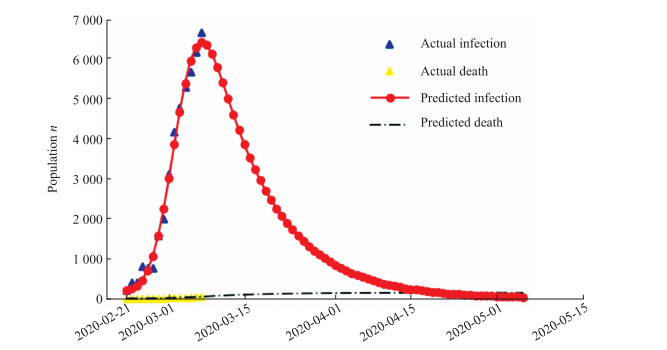
2 结果 2.1 中国湖北省疫情预测

使用求解得到的参数, 通过模型外推, 利用中华人民共和国国家卫生健康委员会发布的截至2020年2月19日的疫情数据, 对截至2020年5月10日湖北省疫情发展情况进行了预测, 结果见图 2。模型预测的湖北省疫情顶点在2月21日, 现有(2020年2月19日)确诊病例数约为50 000例, 2月27日将回落至40 000例以下, 3月4日将回落至30 000例以下, 3月10日将回落至20 000例以下, 3月20日将回落至10 000例以下, 5月10日左右疫情结束。模型预测的累计死亡病例数为6 471例。由于使用常微分方程建模, 因病死亡率在模型中是常数。在疫情消退阶段, 医疗资源被挤占的情况将有所缓解, 实际死亡率会有所下降, 最终因病死亡病例数应少于6 471例。

图 2 湖北省COVID-19疫情预测数据 Fig 2 Prediction data of COVID-19 epidemic in Hubei, China COVID-19: Coronavirus disease 2019

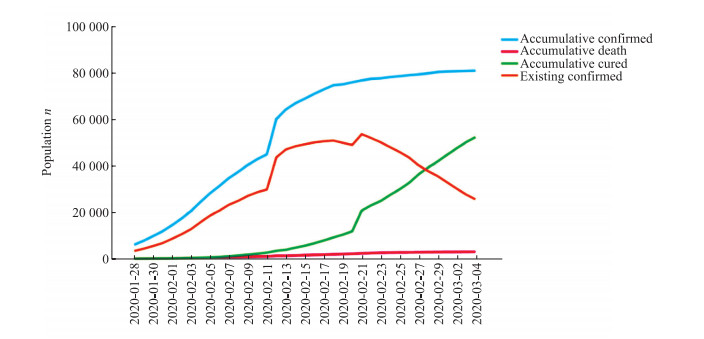
根据中华人民共和国国家卫生健康委员会发布的COVID-19疫情进展数据, 2020年1月28日至3月4日全国COVID-19疫情发展呈现停止上升趋势, 即将出现疫情的顶点(图 3), 湖北省COVID-19疫情也到达顶点(图 2)。

图 3 2020年1月28日至3月4日全国COVID-19疫情实际数据 Fig 3 National actual data of COVID-19 epidemic from Jan. 28 to Mar. 4, 2020 in China COVID-19: Coronavirus disease 2019

2.2 韩国疫情预测

根据中华人民共和国国家卫生健康委员会发布的其他国家COVID-19疫情数据, 根据该模型并按照上述方法类推计算, 得到的韩国COVID-19疫情数据见图 4, 预测韩国疫情峰值在3月7日, 将于4月底结束, 最终累计死亡人数约为141例。但韩国实际疫情数据偏离预测曲线较多, 可能是因为韩国在疫情早期存在大规模集会等社会现象, 部分民众不配合流行病学调查, 导致确诊病例未能及时统计, 数据质量较差。

图 4 韩国COVID-19疫情预测数据 Fig 4 Prediction data of COVID-19 epidemic in South Korea COVID-19: Coronavirus disease 2019

3 讨论

中国疾病预防控制中心COVID-19应急响应机制流行病学组发表的论文中即提出, 在首次发现COVID-19病例后30 d内将波及全国, 截至2020年2月11日有72 314例确诊病例, 在1月23日至26日将到达一个流行病学顶峰, 并可能随着全国复工出现反弹情况[6]。严阅等[7]利用时滞动力学模型预测了COVID-19疫情的发展趋势, 预测在2020年2月9日全国在院治疗病例数达30 000例。周涛等[8]提出了采用传染病动力学SEIR模型关于COVID-19基本再生数R0的预测, 得出此次COVID-19疫情属于传染强度较高的传染病, 提示人群需减少和他人接触, 加强自身防护, 各级部门应尽可能多地采取各种措施救治重型COVID-19患者。根据传染病动力学SEIR模型分析认为, 研究无病平衡点的存在和稳定、调整合适的有关参数有助于流行病学家有效预测疫情的发展趋势[9]。

本研究根据中华人民共和国国家卫生健康委员会发布的数据建立了预测COVID-19疫情发展的SEIR模型。结合预测和实际结果, 疫情在初期没有采取有效防控手段的情况下, 非常符合早期的SEIR模型预测结果, 现有确诊病例数呈指数增长趋势。在疫情发展初期的1个月内, 确诊病例数增长迅速, 当政府相关部门认识到SARS-CoV-2的强感染力并采取了有效手段[10], 政府的干预措施逐渐增强, 全国各地的支援力量也逐渐到达湖北省, 对湖北省各地市的交通进行限行, 武汉市及其周边地区实行战时管制、确诊病例“应收尽收”政策。根据COVID-19最新认识及疫情数据[11-12], 防控措施下的实际疫情发展情况与预期防控效果相符合, 考虑COVID-19潜伏期可长达14 d, 确诊病例增长速度在2月8日达到顶峰, 随后逐渐回落。本研究改进的SEIR模型预测湖北省2月21日现有确诊病例数达到峰值, 表明湖北省防疫工作已经取得阶段性成效。对于韩国的疫情发展, 由于韩国民众在疫情早期不听从政府的防疫劝告, 且存在教会举行大规模集会的社会现象, 导致疫情大规模的阶段性蔓延, 这对于模型的外推精度有较明显的不利影响。日本的疫情数据不准确, 尤其检测条件非常严苛, 可能造成遗漏, 并且早期大部分病例可能来自于“公主号”邮轮, 预测价值不高, 所以没有进行预测。

本研究采用传染病动力学SEIR模型预测COVID-19疫情数据, 有效地预估了疫情的发展趋势, 并且根据Python的数据获取功能不断自动更新未来疫情发展。根据全国累计确诊病例数据, 在当前疫情防控措施的严格执行下, SARS-CoV-2的传播已经如期出现了拐点, 并逐渐下降。未来随着疫情的发展和干预因素的引入, 模型的拟合度仍有待进一步追踪研究。此外, 值得注意的是, 本次疫情处于潜伏期的病例也存在较强传染性, 并且因为部分SARS-CoV-2检测试剂盒的灵敏度低于50%, 检测结果存在假阴性可能, 这均会影响模型预测的准确度。

综上所述, 改进的传染病动力学SEIR模型在COVID-19疫情早期实现了较准确的数据预测, 政府相关部门在疫情中及时、有效的强力干预明显影响了疫情的发展进程, 东亚其他国家如韩国的疫情在3月仍处于上升期, 提示中国需要提防输入性疫情风险。

参考文献
[1]
中华人民共和国国家卫生健康委员会卫生应急办公室.新型冠状病毒肺炎疫情防控[EB/OL].(2020-04-28)[2020-04-28].http://www.nhc.gov.cn/xcs/yqtb/202004/90ee8bf3f47e40d28daef56fdd6da158.shtml.
[2]
耿辉, 徐安定, 王晓艳, 张勇, 尹小妹, 马茂, 等. 基于SEIR模型分析相关干预措施在新型冠状病毒肺炎疫情中的作用[J]. 暨南大学学报(自然科学与医学版), 2020, 41: 175-180.
[3]
WEI F, XUE R. Stability and extinction of SEIR epidemic models with generalized nonlinear incidence[J]. Math Comput Simulat, 2020, 170: 1-15.
[4]
KWOK K O, TANG A, WEI V W I, PARK W H, YEOH E K, RILEY S. Epidemic models of contact tracing: systematic review of transmission studies of severe acute respiratory syndrome and Middle East respiratory syndrome[J]. Comput Struct Biotechnol J, 2019, 17: 186-194.
[5]
中华人民共和国国家卫生健康委员会卫生应急办公室.武汉市卫生健康委员会关于新型冠状病毒感染的肺炎情况通报[EB/OL].(2020-01-20)[2020-01-20].http://www.nhc.gov.cn/xcs/yqtb/202001/a5f1aec0660f4cd3a70518b6258fd15f.shtml.
[6]
中国疾病预防控制中心新型冠状病毒肺炎应急响应机制流行病学组. 新型冠状病毒肺炎流行病学特征分析[J]. 中华流行病学杂志, 2020, 41: 145-151.
[7]
严阅, 陈瑜, 刘可伋, 罗心悦, 许伯熹, 江渝, 等. 基于一类时滞动力学系统对新型冠状病毒肺炎疫情的建模和预测[J]. 中国科学:数学, 2020, 50: 1-8.
[8]
周涛, 刘权辉, 杨紫陌, 廖敬仪, 杨可心, 白薇, 等. 新型冠状病毒肺炎基本再生数的初步预测[J]. 中国循证医学杂志, 2020, 20: 359-364.
[9]
秦爽, 张建刚, 杜文举, 俞建宁, 刘頔. 一类SEIR传染病模型的动力学行为分析[J]. 温州大学学报(自然科学版), 2017, 38: 8-15.
[10]
中国疾病预防控制中心新型冠状病毒肺炎疫情防控流行病学组和防控技术组. 新型冠状病毒肺炎聚集性疫情流行病学调查技术指南(试行第一版)[J]. 中华流行病学杂志, 2020, 41: 293-295.
[11]
中华预防医学会新型冠状病毒肺炎防控专家组. 新型冠状病毒肺炎流行病学特征的最新认识[J]. 中华流行病学杂志, 2020, 41: 139-144.
[12]
ZOU L, RUAN F, HUANG M, LIANG L, HUANG H, HONG Z, et al. SARS-CoV-2 viral load in upper respiratory specimens of infected patients[J]. N Engl J Med, 2020, 382: 1177-1179.