2. 海军军医大学(第二军医大学)海军医学系海军环境与劳动卫生学教研室, 上海 200433
2. Department of Naval Environment and Labor Hygiene, Faculty of Naval Medicine, Naval Medical University(Second Military Medical University), Shanghai 200433, China
战前进行减员评估具有十分重要的意义,它是卫勤组织指挥的主要工作之一。减员评估对于现代海战是一项相当复杂的系统工程,是国内外卫勤领域的一个重大难题,涉及参战双方各类人员的素质、武器杀伤力、战场环境等诸多因素,以及对这些因素的定量描述方法。电子计算机技术和一系列新算法的出现为科学研究提供了新的手段和方法,使减员评估这类复杂的研究课题有可能通过建立数学模型和采取作战模拟的方法进行多次重复性分析研究实现[1-2]。本文在分析水面舰艇受打击特点的基础上,将随机过程中的马尔科夫链(简称马氏链)应用于舰艇被多次命中后的减员评估,给出了计算舰艇作战减员的一种转移概率矩阵方法,提出了在受到多次武器攻击下舰艇上各个系统的作战减员概率评估方法,并对不同系统分布的计算结果进行了比较,为水面舰艇作战减员评估提供了一种有效方法。
1 马氏链的基本原理 1.1 马氏链的定义[3]现实世界中有很多这样的现象:在已知现在情况的条件下,某一系统未来时刻的情况只与现在有关,而与过去的历史无直接关系。描述这类随机现象的数学模型称为马氏模型。考虑舰艇受到打击的时间是离散的,损伤情况也是离散的,且每次打击是独立的、无后效的过程,是一个马氏链,故可用马氏链的相关理论来解决水面舰艇受多次打击问题。
定义1 设{ξn, n=1, 2, …}是一个随机序列,状态空间E为有限或可列集,对于任意的正整数m和n,若i, j, ik∈E(k=1, …, n-1),有
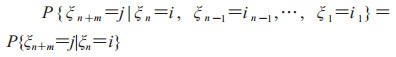
|
(1) |
则称{ξn, n=1, 2, …}为一个马氏链,(1)式称为马氏性。
可以证明若(1)式对于m=1成立,则它对于任意的正整数m也成立。因此,只要当m=1时(1)式成立,就可以称随机序列{ξn, n=1, 2, …}具有马氏性,即{ξn, n=1, 2, …}是一个马氏链。
定义2 设{ξn, n=1, 2, …}是一个马氏链。如果(1)式右边的条件概率与n无关,即

|
(2) |
则称{ξn, n=1, 2, …}为时齐的马氏链。称pij(m)为系统由状态i经过m个时间间隔(或m步)转移到状态j的转移概率。(2)式称为时齐性,它的含义是:系统由状态i到状态j的转移概率只依赖于时间间隔的长短,而与起始的时刻无关。
1.2 转移概率矩阵及柯尔莫哥洛夫定理[4]对于一个马氏链{ξn, n=1, 2, …},称以m步转移概率pij(m)为元素的矩阵P(m)=(pij(m))为马氏链的m步转移矩阵。当m=1时,记P (1)=P称为马氏链的一步转移矩阵,或简称转移矩阵。它们具有下列3个基本性质。
(1)对一切i, j∈E, 0≤pij(m)≤1;
(2)对一切i∈E, 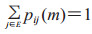
(3)对一切i, j∈E, 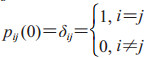
对有限状态空间E={1, 2, …, m},其一步转移概率可写成如下矩阵形式:
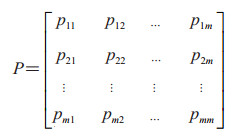
|
(3) |
马氏链的转移概率之间有以下关系:设n=k+l,k≥1,l≥1,则
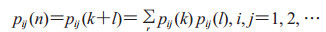
|
(4) |
这就是切普曼-柯尔莫哥洛夫方程[5]。这个方程的直观意义是:要想由i状态出发经k+l步到达状态j,必须先经k步到达任意状态r,然后再经l步转移到j状态。
将(3)式表示为矩阵形式:P(k+l)=P(k)P(l),当取k=1且l=1时,得P(2)=P(1)P(1)=[P(1)]2,当取k=2且l=1时,得P(3)=P(2)P(1)=[P(1)]3,一般地,有P(n)=[P(1)]n。此式表明n步转移概率矩阵等于n个一步转移概率矩阵的乘积,所以可由一步转移概率矩阵获得。因此,在马氏链中一步转移概率矩阵是最基本的,它完全确定了链的状态转移的统计规律。当用马氏链来描述实际问题时,首先要确定状态空间及参数集合,然后确定它的一步转移概率。关于这一概率的确定可以由问题的内在规律得到,也可以由过去经验给出,还可以根据观测数据来估计。
2 基于马氏链的水面舰艇作战减员评估方法考虑水面舰艇被多次打击后的作战减员评估问题,可以发现其第n (n>1)次打击后舰艇损伤减员情况只与第n-1次打击后舰艇的状态有关,而与之前的打击无关,故舰艇多次打击过程具有无后效性,是马尔可夫过程;同时,舰艇遭受打击的时间是离散的,舰艇的损伤情况也是离散的,故多次打击过程是一个马氏链。
2.1 算法说明不同结构的水面舰艇由于其舰体结构、材料强度及舱室布局不同,以及来袭反舰导弹或鱼雷性能的差别,其所能承受的打击次数也不同。
舰艇舱室一般包括以下多种类型。
(1)机、炉舱。机舱设在舰体中部水线以下,内安装主机和辅机,炉舱设在机舱前面。机、炉舱是舰上最大的舱室,也是舰体承受重量最大的部位,因此该舱室的结构较坚固。
(2)油、水舱。它的位置靠近机、炉舱,不仅供应油、水方便,且管路短、重量轻、抗损性强。一般将机、炉舱下双层底的空间做油、水舱。
(3)弹药舱。它的位置在发射武器的附近水线以下,距离机、炉舱和舷部有一定距离。该舱底部常为双层底,可以保持舱内较低温度且不易被敌人武器破坏。
(4)指挥仪、电罗经舱。这2个舱室设在下甲板中段,当舰艇摇摆时较稳定,以减轻对仪器工作的影响。
(5)声纳舱。设在靠近舰首的底部,远离螺旋桨,以避免工作时受螺旋桨噪音的影响。
(6)住舱。人员的住舱通常靠近其战斗部位,一般主甲板以下的舱室为住舱。
(7)医务舱室。为方便舰上各部位伤员的运送且要求颠簸较轻,所以医务舱室一般设在舰体中段。
(8)各种仓库。包括器材配件仓、粮食仓、被服仓等,一般设在下甲板或平台以下的舱室内。
除以上舱室外,舰首端还有锚机舱、锚链舱,舰尾端还有舵机舱等。
不同的舱室所能承受的打击程度不同,其战位人员数量也不同。本文中,定义关键部位是指只需1发命中弹即可摧毁、击沉或使舰艇失去作战能力的部位,例如弹药舱和油、水舱等,设其被命中的概率为P毁。
基本假设如下:①命中概率沿舰船纵向中心轴均匀分布;②命中后不考虑可能带来的二次损伤;③武器破坏半径内的该舱室人员列为减员。
文中符号约定:C(m)为舰艇长度;Ci (i=1, 2, 3, …, n)为各舱室沿纵向中心轴方向长度,n为舱室个数;ri% (i=1, 2, 3, …, n)为舰艇各舱室人员百分比,r为该型舰船人员总数;CP为舰船关键部位的长度。设舰艇舱室的纵向分布如图 1所示。

|
图 1 1某型舰艇舱室及关键部位分布 r1%,r2%,r3%,…,rn%:舰艇各舱室人员百分比;C1,C2,C3,…,Cn:各舱室沿纵向中心轴方向长度;CP:舰船关键部位的长度 |
2.2 水面舰艇舱室命中概率及该舱室相应减员概率的计算
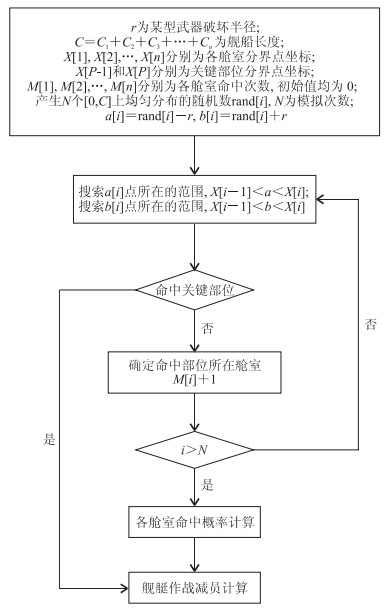
采用蒙特卡洛法计算1次命中后各舱室的损坏概率,思路是:已知预定武器的命中散布,采用蒙特卡洛法模拟各舱室累加命中次数,累加次数除以模拟次数即可得出1次命中后各舱室的损坏概率,进而由舰艇各舱室人员百分比计算出该舱室相应减员程度概率。具体计算流程如图 2所示。
|
图 2 舱室命中概率及减员计算流程图 |
2.3 计算一步转移概率
由切普曼-柯尔莫哥洛夫方程,P(n)=[P(1)]n,即损伤n步转移概率矩阵可由损伤一步转移概率矩阵获得。进行多次打击计算实际上就是要求我们计算出受到n次打击后舰艇处于某一损伤状态的概率[1]。这就意味着:在已知初始状态的情况下,要计算舰艇受到n次打击后处于某一损伤等级的概率必须要求出舰艇的n步转移概率矩阵P(n),而P(n)=[P(1)]n,至此,多次打击问题最后归结为求一步转移概率矩阵的问题。若要得到一步转移概率矩阵,必须求出矩阵中的每一个元素Pij。再计算时可依然采用蒙特卡洛法,模拟二次打击(第二次打击的模拟建立在第一次打击后舰艇发生损伤的基础上),将第一次打击和第二次打击后舰艇的损伤情况进行比对,然后,根据比对结果,将损伤由状态i (i∈E)转向状态j (j∈E)统计次数累加;最后将状态i (i∈E)转向状态j (j∈E)累加次数除以模拟次数,即可得出损伤一步转移概率矩阵P(1)。
2.4 水面舰艇遭受多次命中时的减员评估由一步转移概率P(1)可计算出水面舰艇经受n次打击后的概率P(n),进而可计算出各舱室命中概率,进而由舱室战位人员分布情况计算出舰艇减员情况。
3 模型应用示例设某型舰艇的纵向系统分布如图 3所示,舰艇长C为100 m,设武器破坏半径为5 m。则该型舰艇5次被命中的减员计算过程如下:

|
图 3 某型舰艇系统的纵向分布图 C1、C2、C3、C4:沿纵向中心轴方向分布的4个舱室;L1、L2、L3、L4:4个舱室的长度;CP:关键部位舱室;LP:关键部位舱室长度 |
第1次命中,确定状态空间:S1={0},S2={50%},S3={35%},S4={15%},S5={50%, 35%},S6={100%}。水面舰艇舱室第1次被命中时的减员概率计算如下:PS1=5%,PS2=20%,PS3=25%,PS4=24%,PS5=10%,PS6=16%。
第2次命中,确定状态空间:S1={0},S2={50%},S3={35%},S4={15%},S5={50%, 35%},S6={50%, 15%},S7={35%, 15%},S8={100%}。将水面舰艇舱室第2次被命中时的减员概率写入矩阵P(1)中,由第3步计算可得一步转移概率矩阵(矩阵内数值均为百分数)
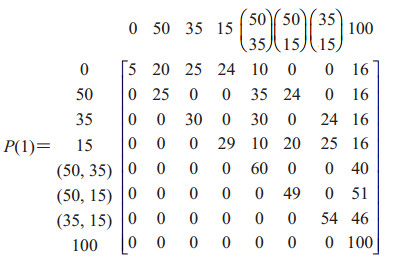
|
第3次命中,P(3)=[P(1)]3;第4次命中,P(4)=[P(1)]4;第5次命中,P(5)=[P(1)]5。
某型舰艇舱室5次被命中后该舱室相应减员概率的模拟计算结果见表 1。
|
|
表 1 某型舰艇舱室5次被命中减员概率的模拟计算结果 |
通过仿真计算可知,舰艇战伤减员与舰艇舱室结构、舰艇舱室人数、武器破坏半径、武器命中次数等有很大关系。随着舰艇被命中次数的增加,减员向大概率状态转移,战伤减员数会明显增加。因此,为降低战伤减员数,除加强战场救护外,还应强化舰艇防护能力,特别是加强舰艇关键部位的防护等。
本文通过分析舰艇被多次命中的特点,将随机过程中的马氏链应用于舰艇被多次命中后的减员评估,给出了具体的计算过程和仿真流程,并通过示例分析了舰艇在多次命中下的战伤减员状况,为水面舰艇减员评估提供了一种新的方法。由于不同型号的舰艇舱室结构有很大的不同、被命中后舱室内的系统不一定完全失效、对舱室人员也可能存在二次损伤等不确定因素,水面舰艇减员评估有待进一步研究和探讨。
| [1] |
黄斌, 程智斌, 鄢宏峰. 舰艇系统遭受多次命中时的损伤评估[J]. 中国舰船研究, 2006, 1: 36-40. |
| [2] |
葛文斌, 赵洪伟, 张国春. 舰艇编队交战战损计算方法研究[J]. 科学技术与工程, 2009, 9: 1072-1075, 1079. |
| [3] |
唐宇, 迟卫, 谢田华. 基于马尔可夫链的舰艇生命力评估[J]. 舰船科学技术, 2003, 25: 9-11. |
| [4] |
董庆华, 王成伟. 马尔可夫链在高等数学教学效果评价中的应用[J]. 数学的实践与认识, 2018, 8: 314-320. |
| [5] |
汪荣鑫. 随机过程[M]. 西安: 西安交通大学出版社, 2002: 83-87.
|
 2020, Vol. 41
2020, Vol. 41


