2. 上海中医药大学基础医学院中医诊断教研室, 上海 201203
2. Department of Traditional Chinese Medicine Diagnosis, Basic Medical College, Shanghai University of Traditional Chinese Medicine, Shanghai 201203, China
将人工智能技术应用于中医临床诊断领域,将可能有效提高中医临床脉图参数变化及血压的预测精度。目前常用的预测方法有过程神经网络[1]、支持向量机(support vector machine,SVM)[2]等。朱群雄和甄玉山[3]采用过程神经网络方法,利用主成分分析表征参数间相关性,将拟合过程作为神经网络输入,建立软测量模型实现主变量的连续预测,但该方法易陷入局部极小点并出现过拟合现象。SVM方法基于结构风险最小化准则,其拓扑结构由支持向量决定,克服了人工神经网络(artificial neural network,ANN)过度依赖设计者经验的缺点,兼顾了神经网络和灰度模型的优点[4-5]。因此,国内有些学者提出了基于粒子群优化(particle swarm optimization,PSO)算法的SVM预测模型。王保义等[6]通过引入Spark on YARN内存计算平台并采用基于改进并行粒子群优化(improved parallel particle swarm optimization,IPPSO)算法,对不确定参数进行优化。陈进东和潘丰[7]通过改进粒子群中的学习因子对数据样本进行短期预测,发现较标准SVM算法有较好的预测效果,但该方法精度不足,实时性较差,且仅限于小样本数据分类测试。
最小二乘支持向量机(least square support vector machine,LSSVM)是标准SVM的一种扩展,用等式约束代替SVM的不等式约束,即将二次规划问题转化为线性方程求解问题,降低计算的复杂性,加快求解速度和提高抗干扰能力[8-11]。本研究将SVM理论引入中医临床脉图参数及血压预测过程,提出一种基于LSSVM学习模型,分别采用多项式核函数和径向基核函数对患者临床脉图参数进行学习和训练,并对患者血压进行分析与预测。
1 LSSVM算法分析命题:如果用SVM的不等式约束代替等式约束,将误差平方和损失函数作为训练集的经验损失,那么可得到LSSVM函数估计为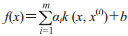
证明:SVM是通过一个非线性映射φ(x(i))将样本输入数据映射到一个高维特征空间,从而将实际问题转化为一个带不等式约束的二次规划问题[12-13]。假设一组训练样本为(x(i), y(i)), i=1, 2, …, m,其中x∈Rn为系统样本输入,y∈R为系统输出,i为样本序号。则SVM优化问题可形式化为

|
(1) |
式中w为超平面法向量,γ为几何间隔,b为截距,i为样本序号。将目标函数优化修改为二次规划问题,即目标函数改写成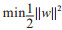
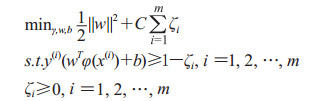
|
(2) |
式中w为超平面法向量,γ为几何间隔,b为截距,ζi为松弛变量,i为样本序号。用SVM不等式约束代替等式约束,LSSVM优化目标可表示为
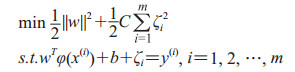
|
(3) |
式中w为超平面法向量,C为误差惩罚系数,ζi为松弛变量,i为样本序号。构造拉格朗日函数为
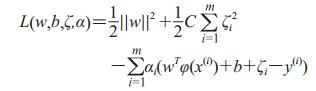
|
(4) |
式中αi为拉格朗日算子,w为超平面法向量,γ为几何间隔,b为截距,ζi为松弛变量,i为样本序号。根据KKT条件得到下式
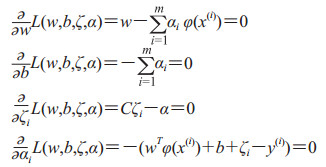
|
消去w和ζi得到:
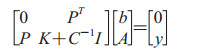
|
(5) |
其中P=[1, 1, …, 1]T, A=[α1, α2, …, αm]T, y=[y1, y2, …, ym]T, K是一个核函数矩阵,Kij=φ(x(i))T φ(x(i))=k (x(i), x(j)),得到LSSVM函数估计为
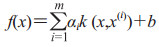
|
(6) |
核函数k可选用径向基核函数

|
(7) |
径向基核函数中的核参数g、惩罚参数C可选用梯度下降算法进行寻优,核参数g和惩罚参数C更新公式为

|
(8) |
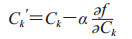
|
(9) |
式中α为学习率。核函数k也可选用多项式核函数
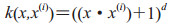
|
(10) |
LSSVM模型采用交叉验证Hold-Out算法分割测试样本和训练样本,该方法可应用于中医脉诊中的血压预测。
2 实验步骤通过LSSVM学习模型对患者进行血压预测。脉图参数(输入)主要包括主波幅度(h1)、重波前波幅度(h3)、反映血管壁顺应性和动脉血管外周阻力状态参数h3/h1、反映动脉血管外周阻力状态参数h4/h1(h4为降中峡幅度)、主波上1/3处宽度(w)、反映动脉管壁弹性和外周阻力大小参数w/t(t表示脉图起点到终止点的时值)、反应心脏射血功能参数t1/t(t1为脉图起点到主波峰点的时值)等[15]。血压参数(输出)包括舒张压(diastolic blood pressure,DBP)、收缩压(systolic blood pressure,SBP)、平均动脉压(mean arterial pressure,MAP)。
定义1例患者的输入参数(脉图)和输出参数(血压)为1组样本。本研究收集320组患者的临床脉图参数和血压数据,其中300组样本为训练样本,20组为测试样本。通过多项式核函数(公式10)与径向基核函数(公式7)分别训练得到LSSVM学习模型,将样本的脉图参数作为模型输入的特征得到预测血压输出,并将20组测试样本的LSSVM学习模型预测结果与临床测得患者实际血压进行比较。
LSSVM预测过程包括:(1)数据预处理。根据需要预测的样本数据特征选用所有样本中1~300组样本作为LSSVM训练样本,选取301~320组样本作为测试样本。并将训练样本进行归一化预处理,归一化方法选用mapminmax函数,样本数据归一化到区间[0, 1]。(2)LSSVM参数初始化。核函数选用多项式核函数(公式10)与径向基核函数(公式7)进行比较,其中核参数g和惩罚系数C均初始化为0.1。(3)建立学习模型。根据LSSVM的算法编写程序输入训练样本(x(i), y(j)),通过批量梯度下降迭代得到最优核参数g和惩罚参数C,根据所得参数建立LSSVM学习模型。随后输入预测样本的输入向量x(i),通过LSSVM学习模型预测出输出向量y(j),并与测试样本实际输出向量进行对比得到误差。
3 实验结果和分析收集320组患者的临床脉图参数及血压数据,对300组训练样本进行训练得到LSSVM学习模型,对其余20组患者临床脉图参数及血压数据进行测试。对LSSVM学习模型使用批量梯度下降算法(batch gradient descent)训练最优参数,每迭代一步,均要用到训练集所有的数据,如果训练样本的损失函数为凸函数就能保证收敛到最优值。由于本实验中训练样本规模小,因此批量梯度算法使训练过程既能保证足够的精确度,又有较好的实时性。图 1所示离散点分别为DBP(蓝色)、SBP(红色)、MAP(黑色)实际数据及其拟合曲线,图中可见LSSVM学习模型拟合曲线能够反映数据样本分布和特点。

|
图 1 训练样本输出拟合曲线 Fig 1 Output fitting curves of training samples 1 mmHg=0.133 kPa. DBP: Diastolic blood pressure; SBP: Systolic blood pressure; MAP: Mean arterial pressure |
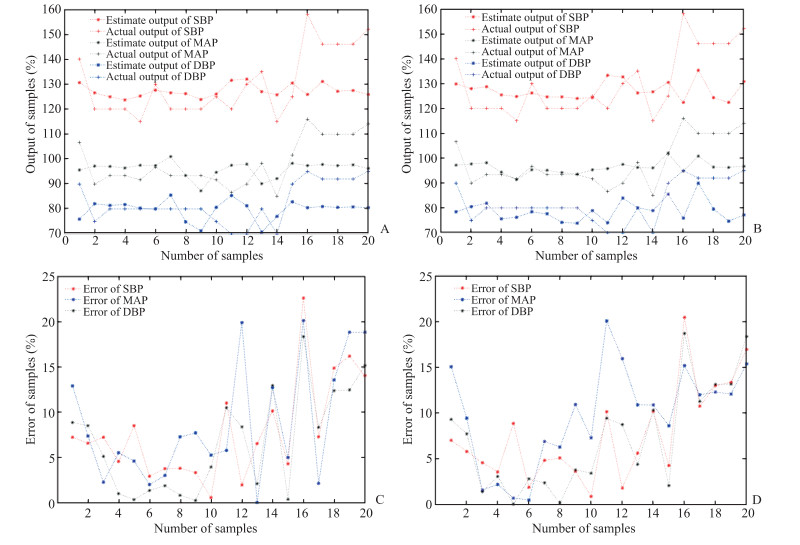
针对训练所得的LSSVM学习模型,对剩余20组样本进行测试。图 2A、2B分别给出基于径向基核函数的LSSVM学习模型与基于多项式核函数的LSSVM学习模型输出对比曲线。图 2C、2D分别给出基于径向基核函数的LSSVM学习模型与基于多项式核函数的LSSVM学习模型误差曲线。
|
图 2 基于径向基核函数和多项式核函数LSSVM学习模型输出与误差曲线 Fig 2 Output and error curves of LSSVM learning model based on radial basis kernel function and polynomial kernel function A: Output contrast of radial basis function kernel model; B: Output contrast of polynomial kernel model; C: Error curve of radial basis function kernel model; D: Error curve of polynomial kernel model. LSSVM: Least square support vector machine; DBP: Diastolic blood pressure; SBP: Systolic blood pressure; MAP: Mean arterial pressure |
从图 2A、2B可见,多数样本点预测结果与实际数据差距较小,其中1~10号测试样本预测结果与实际结果更为接近。图 2C、2D结果显示,第3、4、5、6号样本的预测准确度较高。在本研究中采用基于多项式核函数的LSSVM学习模型中SBP、DBP、MAP预测结果的平均预测误差分别为7.88%、8.40%、6.67%,基于径向基核函数的LSSVM学习模型的预测误差分别为7.95%、9.70%、7.48%,与基于多项式核函数LSSVM学习模型相比,平均预测误差分别增加了0.89%、15.48%、12.14%。从训练时间分析,2种核函数的LSSVM学习模型训练时间均约为0.37 s,具有较好的实时性。
分析LSSVM学习模型预测的误差数据,基于多项式核函数的学习模型测试的样本具有较好的预测效果,这是由于梯度下降算法容易陷入局部最优,基于径向基核函数的LSSVM学习模型寻优核参数g和惩罚参数C时不能在有限迭代次数内获得全局最优参数,而多项式核函数属于全局核函数,对相距较远的样本点具有更好的预测效果,因此基于径向基核函数的LSSVM学习模型的预测误差较高。
综合对比,基于多项式核函数的LSSVM学习模型表现出对中医脉图参数-血压数据样本更好的学习和预测能力。多项式核函数适合于正交归一化的样本数据,属于全局核函数,相距较远的数据点对核函数值也会产生影响,本研究选用合适的指数参数d可有效减小高维度样本数据导致的较大计算量。对于本实验中的数据样本,基于多项式核函数LSSVM模型具有比径向基核函数模型更好的学习能力。由图 2C、2D可见,基于多项式核函数LSSVM学习模型的预测误差均较基于径向基核函数学习模型低,但2种核函数LSSVM学习模型误差均整体呈升高趋势,这是因为本实验中样本处理选用标准交叉验证Hold-Out算法获得训练样本和测试样本,该算法易造成数据浪费,使测试阶段辨识率降低,部分数据出现较高误差。
4 结论本研究提出一种基于LSSVM的学习模型,通过对临床脉图参数进行学习和训练,从而预测样本血压数据,并比较基于径向基和多项式核函数的LSSVM学习模型,发现基于多项式核函数的LSSVM学习模型较基于径向基核函数LSSVM学习模型表现出更好的学习和预测能力。今后我们将进一步改进并优化LSSVM学习模型及其参数。在临床应用中,我们提出的基于LSSVM学习模型仅通过患者的临床脉图参数就可预测患者血压数据,有助于减轻医师的工作量和患者负担,此外其也可推广应用于其他临床数据的预测。
| [1] |
彭显刚, 胡松峰, 吕大勇. 基于RBF神经网络的短期负荷预测方法综述[J]. 电力系统保护与控制, 2011, 39: 144-148. |
| [2] |
丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40: 2-10. DOI:10.3969/j.issn.1008-8105.2011.04.002 |
| [3] |
朱群雄, 甄玉山. 用于化工软测量的基于移动窗的过程神经网络[J]. 清华大学学报(自然科学版), 2012, 52: 1165-1170. |
| [4] |
SAIN S R, VAPNIK V N. Book review:the nature of statistical learning theory[J]. Technimetrics, 1996, 38: 409. |
| [5] |
VAPNIK V N. An overview of statistical learning theory[J]. IEEE Trans Neural Netw, 1999, 10: 988-999. DOI:10.1109/72.788640 |
| [6] |
王保义, 王冬阳, 张少敏. 基于Spark和IPPSO_LSSVM的短期分布式电力负荷预测算法[J]. 电力自动化设备, 2016, 36: 117-122. |
| [7] |
陈进东, 潘丰. 基于在线支持向量回归的非线性模型预测控制方法[J]. 控制与决策, 2014, 29: 460-464. |
| [8] |
SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Process Lett, 1999, 9: 293-300. DOI:10.1023/A:1018628609742 |
| [9] |
WANG H Q, SUN F C, CAI Y N, DING L G, CHEN N. An unbiased LSSVM model for classification and regression[J]. Soft Computing, 2010, 14: 171-180. DOI:10.1007/s00500-009-0435-z |
| [10] |
DE KRUIF B J, DE VRIES T A. Pruning error minimization in least squares support vector machines[J]. IEEE Trans Neural Netw, 2003, 14: 696-702. DOI:10.1109/TNN.2003.810597 |
| [11] |
林升梁, 刘志. 基于RBF核函数的支持向量机参数选择[J]. 浙江工业大学学报, 2007, 35: 163-167. DOI:10.3969/j.issn.1006-4303.2007.02.010 |
| [12] |
胡瑾秋, 郭放, 张来斌. 结合改进PSO算法和LSSVM的化工异常工况超早期监测预警研究[J]. 电子测量与仪器学报, 2018, 32: 36-41. |
| [13] |
LI L, SU H, CHU J. Modeling of isomerization of C8 aromatics by online least squares support vector machine[J]. Chin J Chem Eng, 2009, 17: 437-444. DOI:10.1016/S1004-9541(08)60228-1 |
| [14] |
郑蓉建, 潘丰. 基于PLS-LSSVM的谷氨酸发酵产物浓度预测建模[J]. 化工学报, 2017, 68: 976-983. |
| [15] |
朱丽萍, 吴宏进, 张志枫, 张瑜, 许家佗, 屠立平, 等. 54例不同性别健康大学生"寸口"脉象及脉图参数分析[J]. 上海中医药大学学报, 2013, 27: 28-31. |
 2019, Vol. 40
2019, Vol. 40


