2. 军事科学院军事医学研究院, 北京 100850
2. Academy of Military Medical Sciences, Academy of Military Sciences, Beijing 100850, China
炭疽芽孢杆菌被广泛认为是威胁最大的生物恐怖剂,尤其是在人口密集区域以气溶胶的形式扩散将对人群健康、生态环境、社会经济等造成巨大危害[1]。炭疽生物事件的危害后果受多种因素影响,包括事件情景、医学干预介入时间、关键资源准备水平、资源的规划使用策略等,评估这些因素对危害后果的影响对于有效应对此类生物威胁具有重要意义,主要体现在:(1)在应急准备阶段,为关键资源的储备建设提供依据,回答“什么样的资源准备水平可以将风险控制在可接受的范围”;(2)在应急响应阶段,为资源规划方案的制订提供决策支持,提高关键资源的使用效率[2]。
基于此,Wein和Craft等通过建立疾病发展模型和干预策略等模型,探讨了事件发生后哪些人应优先获得医学干预,评估了暴露前预防和暴露后预防等4种干预策略的效果[3-5];Jamrog等[6]基于马尔科夫链模拟事件应急响应过程,提出抗生素分发能力是影响干预效果的关键因素;Zaric等[7]利用动态仓室状态转移模型,评估了美国地方医疗资源储备策略、国家战略储备物资的调用策略、资源分发策略及策略代价;Chen等[8]建立了疾病状态发展的多周期模型,基于抗生素分发站点构建的相关政策方案,评估了抗生素分发策略、抗生素分发站点分发能力等对干预效果的影响。在模型运用方面,美国疾病控制与预防中心(Centers for Disease Control and Prevention,CDC)基于Zaric等[7]提出的动态仓室状态转移模型,开发了一种名为Anthrax Assist的工具,为公共卫生官员提供吸入性炭疽案例的快速预测和气雾化炭疽事件中的响应决策支持[9]。
上述这些研究主要从群体层面建模,描述群体在仓室之间的流通。实际上不同个体吸入的炭疽芽孢数量、感染后发展到相应病程阶段的时间以及接受医疗干预的时间等均存在差异,前述方法无法描述这种差异,在一定程度上会影响评估结果。另外,炭疽恐怖事件具有典型的情景依赖性,事发场所、处置机制、危害大小等均具有地域差别,目前国内尚缺乏相关的定量研究。本研究以我国大城市遭受炭疽芽孢气溶胶恐怖袭击为想定背景,从个体层面建立一种针对炭疽生物恐怖危害后果的定量评估方法,为医学救援能力建设、应急策略选择提供参考。
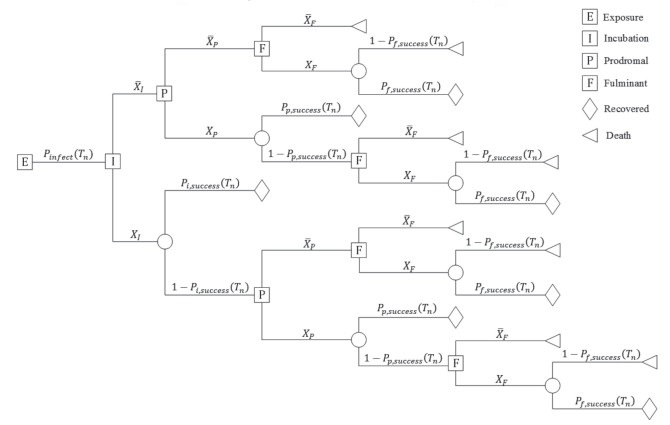
1 暴露个体医学干预措施建模 1.1 炭疽暴露后的病程发展路径个体在暴露于炭疽芽孢气溶胶后可能发生感染、发病和死亡,在此事件链发展的不同阶段对个体实施医学干预均可改变其病程发展的路径,降低发病或死亡的概率。为量化炭疽病例病程发展的可能路径,基于决策树概念模型,本研究构建了在不同病程发展阶段对炭疽暴露者实施医学干预的决策树模型,见图 1。
|
图 1 医学干预下吸入性炭疽病程发展的决策树 Fig 1 Decision tree for the development of inhaled anthrax in medical intervention XI, XP and XF, and XI, XP and XF represent getting treatment, and getting no treatment during the incubation period, prodromal period and fulminant period, respectively; Pinfect(Tn) is the infection rate after exposure to anthrax aerosol; Pi, success(Tn), Pp, success(Tn) and Pf, success(Tn) are the rates of recovery after treatment during the incubation period, prodromal period and fulminant period, respectively |
(1)暴露后感染概率:
个体暴露(exposure,E)于炭疽芽孢气溶胶后,在未接受医学干预措施的情况下其感染概率为Pinfect(Tn),取值与个体在Tn时刻累计吸入炭疽芽孢的数量D(Tn)相关,计算公式[10]为:
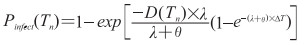
|
(1-1) |
其中,λ为体内炭疽芽孢萌发率,取值为5×10-6/d;θ为体内炭疽芽孢清除率,取值为0.07/d。D(Tn)计算公式[10]如下:
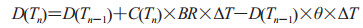
|
(1-2) |
BR(breathing rate)为个体呼吸频率,表示单位时间内吸入的空气容量(m3/h),白天和夜晚的取值分别为0.9 m3/h和0.45m3 /h[11-12];ΔT为仿真步长(0.5 h);C(Tn)为Tn时刻个体所处环境中炭疽芽孢浓度,该浓度通过气溶胶扩散模型获得[13]。
(2)潜伏期及预防效果:
潜伏期(incubation,I)持续时间可用对数正态分布进行描述,分布参数与个体累计吸入炭疽芽孢数量相关。潜伏期中位数M和标准差σ的计算公式[14]为:
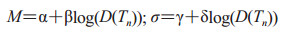
|
(1-3) |
D(Tn)为Tn时刻个体累计吸入的炭疽芽孢数量,α、β、γ和δ为计算参数,取值分别为10.3、-1.35、0.804和-0.079。
感染者在潜伏期口服抗生素预防(XI)[15]后的康复率Pi, success(Tn)随介入时间的延迟线性递减,计算公式[8]如下:
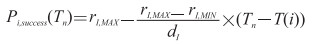
|
(1-4) |
rI, MAX为潜伏期抗生素预防最大康复率,常用取值范围为80%~100%,本研究取值为80%;rI, MIN为接受预防后的最小康复率,等于前驱期接受治疗的最大康复率;dI为潜伏期平均时间(10.3 d);T(i)为个体进入潜伏期的时间;Tn为个体接受抗生素预防的时间。假设未接受抗生素预防的感染者100%发展到前驱期。
(3)前驱期及治疗效果:
前驱期(prodromal,P)持续时间可用韦伯分布或对数正态分布来描述[16]。本研究采用对数正态分布建模前驱期时间长度,在未经治疗的情况下平均时间为4.2 d,标准差为2.3 d;在获得治疗的情况下平均时间为5.8 d,标准差为2.0 d。
感染者在前驱期接受治疗(XP)[15]后的康复率Pp, success(Tn)随介入时间的延迟线性递减,计算公式[8]如下:
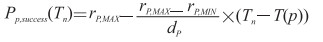
|
(1-5) |
rP, MAX为前驱期接受治疗的最大康复率,常用取值范围为20%~40%,本研究取值为20%;rP, MIN为接受治疗后的最小康复率,等于症状明显期接受治疗的康复率;dP为未经治疗时前驱期平均时间(4.2 d);T(p)为个体进入前驱期的时间;Tn为个体接受前驱期治疗的时间。假设未接受治疗的感染者100%发展到症状明显期。
(4)症状明显期及治疗效果:
症状明显期(fulminant,F)持续时间同样可以使用韦伯分布或对数正态分布描述[16]。本研究采用对数正态分布建模症状明显期时间长度,在未经治疗的情况下平均时间为0.7 d,标准差为0.74 d;治疗开始于前驱期时平均时间为1.4 d,标准差为1.8 d;治疗开始于症状明显期时平均时间为1.5 d,标准差为1.3 d。
感染者在症状明显期接受治疗(XF)[15]后的康复率Pf, success(Tn)常用取值范围为0~3.2%,本研究取值为3.2%。因症状明显期的持续时间很短,且救治后康复率极低,忽略其随介入时间延迟的递减情况。假设在此阶段未获得治疗的感染人员100%死亡。
1.2 医学干预的资源配置标准实施各阶段医疗干预措施(XI、XP、XF)均需动用药品、人员、装备、设施等资源。基于此,本研究定义了各干预措施资源使用配置标准,用于量化评估不同资源储备水平对干预策略实施的约束[17-18]。
策略模拟中通过计算个体接受医疗干预的概率Px, select(Tn)来表达这种约束关系。计算公式如下:
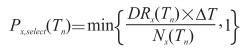
|
(1-6) |
Nx(Tn)为Tn时刻疾病状态为x的总人数,x∈{I, P, F};DRx(Tn)为Tn时刻资源状态可干预的人数,计算公式如下:
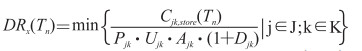
|
(1-7) |
Cjk, store(Tn)为Tn时刻j类资源中第k种资源的剩余量,Pjk、Ujk、Ajk、Djk分别为j类资源中第k种资源被选择使用的概率、使用标准、轮班系数和在使用中的损耗率,J为资源大类,K为资源小类。
DRx(Tn)实际上表示资源储备在Tn时刻能够服务人数的最小值,例如在暴露预防阶段,假设Tn时刻药品分发员的储备量只能服务1 000人,且为所有相关资源中储备量最低,那么DRI(Tn)=1 000人。
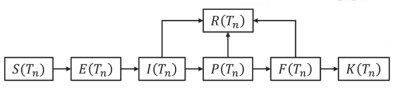
2 人群状态转移队列由于个体疾病发展过程的随机性,在袭击后的任意时间T处于潜伏、前驱症状、明显症状、死亡/康复状态的人群数量是不断变化的,本研究用状态转移队列模型来模拟不同病程状态的人群数量变化过程。定义s为易感个体,s∈S(Tn),S(Tn)为Tn时所有易感个体组成的集合,即易感队列。同理定义暴露队列E(Tn)、潜伏期队列I(Tn)、前驱期队列P(Tn)、症状明显期队列F(Tn)、康复队列R(Tn)和死亡队列K(Tn),队列之间的转移过程如图 2所示。
|
图 2 人群状态转移 Fig 2 Population state transition S(Tn): All susceptible individuals; E(Tn): Exposured individuals; I(Tn): Individuals in the incubation period; P(Tn): Individuals in the prodromal period; F(Tn): Individuals in the fulminant period; R(Tn): Recovered; K(Tn): Death |
2.1 易感队列人群转移
易感队列为所有未吸入炭疽芽孢的易感个体组成的集合,用S(Tn)表示。易感队列在时间[Tn-1, Tn]内的变化只考虑一种情况,即吸入炭疽芽孢进入暴露队列的个体ES→E(Tn),计算公式如下:
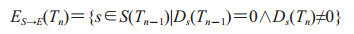
|
(2-1) |
Ds(Tn)为易感个体s在Tn时刻累计吸入炭疽芽孢的数量,计算同公式(1-2)。
2.2 暴露队列人群转移暴露队列为所有吸入炭疽芽孢但未感染的个体组成的集合,用E(Tn)表示。暴露队列在时间[Tn-1, Tn]内的变化主要有两种情况:(1)新进入暴露队列的个体ES→E(Tn),计算同公式(2-1)。(2)感染后进入潜伏期队列的个体EE→I(Tn),计算公式如下:
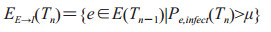
|
(2-2) |
Pe, infect(Tn)为暴露个体e在Tn的感染概率,计算同公式(1-1);μ为来自于U(0, 1)分布的随机数。
2.3 潜伏期队列人群转移潜伏期队列为所有感染后处于潜伏期的个体组成的集合,用I(Tn)表示。潜伏期队列在时间[Tn-1, Tn]内的变化主要有3种情况:(1)新进入潜伏期队列的个体EE→I(Tn),计算同公式(2-2)。(2)接受潜伏期预防干预下由潜伏期队列进入康复队列的个体II→R(Tn),计算公式如下:
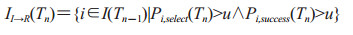
|
(2-3) |
Pi, select(Tn)为Tn时刻个体i被选择接受医疗干预的概率,计算同公式(1-6);Pi, success(Tn)为个体i在Tn时刻接受医疗干预后的康复率,计算同公式(1-4)。接受预防未进入康复队列的个体返回潜伏期队列,等待进入前驱期。
(3)由潜伏期队列进入前驱期队列的个体II→P(Tn),计算公式如下:
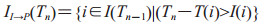
|
(2-4) |
T(i)为感染个体i进入潜伏期的时间;I(i)为其处于潜伏期的时间长度,计算同公式(1-3)。
2.4 前驱期队列人群转移前驱期队列为所有处于前驱期的个体组成的集合,用P(Tn)表示。前驱期队列在时间[Tn-1, Tn]内的变化主要有3种情况:(1)由潜伏期队列进入前驱期的个体II→P(Tn),计算同公式(2-4)。(2)接受前驱期治疗,由前驱期队列进入康复队列的个体PP→R(Tn),计算公式如下:
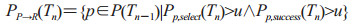
|
(2-5) |
Pp, select(Tn)为Tn时刻个体p被选择接受前驱期治疗的概率,计算同公式(1-6);Pp, success(Tn)为其接受前驱期治疗后的康复率,计算同公式(1-5)。接受治疗未进入康复队列的个体返回前驱期队列,等待进入症状明显期。
(3)由前驱期队列进入症状明显期队列的个体PP→F(Tn),计算公式如下:
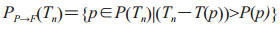
|
(2-6) |
T(p)为个体p进入前驱期的时间;P(p)为其处于前驱期的时间长度,服从对数正态分布,分布参数根据是否接受过治疗取值。
2.5 症状明显期队列人群转移症状明显期队列为所有处于症状明显期的个体组成的集合,用F(Tn)表示,在时间[Tn-1, Tn]内的变化主要有3种情况:(1)由前驱期队列进入症状明显期的个体PP→F(Tn),计算同公式(2-6)。(2)接受症状明显期治疗后进入康复队列的个体FF→R(Tn),计算公式如下:
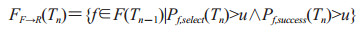
|
(2-7) |
Pf, select(Tn)为Tn时刻个体f被选择接受症状明显期治疗的概率,计算同公式(1-6);Pf, success(Tn)为其接受治疗后的康复率。接受治疗未进入康复队列的个体返回症状明显期队列,等待进入死亡队列。
(3)由症状明显期队列进入死亡队列的个体FF→K(Tn),计算公式如下:
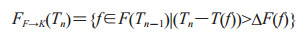
|
(2-8) |
T(f)为个体f进入症状明显期的时间;F(f)为其处于症状明显期的时间长度,服从对数正态分布,分布参数根据治疗情况取值。
2.6 死亡队列人群转移死亡队列个体只来自症状明显期一种情况,Tn时刻新增数量,计算公式为:
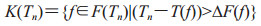
|
(2-9) |
康复队列个体可能来自潜伏期、前驱期和症状明显期,Tn时刻新增数量,计算公式为:

|
(2-10) |
本研究假定北京市于2014年4月28日上午7点遭受炭疽恐怖袭击,源强为10 kg炭疽芽孢气溶胶(1015/kg炭疽芽孢),释放点为东经116.363°、北纬39.9°。采用中尺度数值天气模式产生微环境气象条件,结合拉格朗日粒子扩散模型模拟气溶胶扩散过程,计算环境中气溶胶浓度。暴露区域人口数量为100.83万人。
3.2 干预策略干预策略主要考虑干预延迟时间和资源储备量2个因素,介入延迟时间共分13组,分别为事件发生后1、13、25、37、49、61、73、85、97、109、121、133、145 h。资源储备量分为4个水平,分别为100%、75%、50%、25%。其中假设的100%水平资源储备量包括环丙沙星78 660 000 g,多西环素6 900 000 g,克林霉素21 735 000 g,流行病调查员10 000人,人体暴露洗消员12 000人,抗生素分发员5 000人,传染病医师16 500人,重症监护病房床位20 000张,以及呼吸机20 000台等。
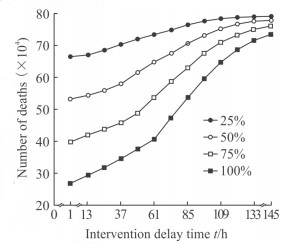
3.3 结果分析根据本研究构建的炭疽恐怖事件医学干预效果定量评估方法和想定情景,计算52种不同干预策略下的事件后果如图 3所示。
|
图 3 不同干预策略下的死亡人数 Fig 3 Number of deaths under different intervention strategies |
干预效果对介入延迟时间和资源储备量2个因素均敏感,最理想情况下(介入延迟时间1 h+100%资源储备)死亡人数为26.63万,而在最坏情况下(介入延迟时间145 h+25%资源储备)死亡人数为79.08万,即储备相对充分的应急资源、在第一时间开展大规模医学干预行动可减少死亡人数约66.33%。
资源储备量对死亡人数的影响随介入时间延迟的增加递减,介入延迟1 h、资源投入为25%时,死亡人数为66.43万,资源提高到100%时死亡人数为26.63万,减少死亡人数的比例为59.91%。同样将资源由25%提高到100%的情况下,介入延迟时间为49、97、145 h,减少死亡人数的比例分别为47.97%、23.39%和7.33%。出现这种递减效应的原因是介入时间严重延迟后已有大量人群发病,在这种情况下即便具有足够的医学资源,其作用也非常有限。及早发现和判定事件性质是有效缩短介入延迟时间的前提,这提示了事件早期监测预警能力的重要性。
在实施不同医疗干预策略下发病人数达到峰值的平均时间约为事件爆发后10.14 d(表 1),标准差为0.33 d;峰值人数的最大值为255 072人,最小值为103 943人,平均值为206 580人,标准差为56 555人。干预策略对发病人数达到峰值的时间影响较小,对峰值人数的影响较大,即当医疗干预介入延迟时间较短、投入的资源较大时,能明显降低峰值人数;当投入资源水平较低时,即使介入延迟时间较短,其期峰值人数依然较高,对医疗资源需求的冲击依然较大。
|
|
表 1 干预策略与发病人数峰值及峰值时间的关系 Tab 1 Relationship between intervention strategies and peak value and peak time of morbidity |
4 讨论
本研究通过建立炭疽暴露后医学干预的决策树模型、资源消耗配置模型和人群状态转移模型,并基于离散事件系统仿真方法对多种干预策略进行了效果评估,初步建立了具有情景特征的炭疽事件医学处置效果的量化评估方法。该方法在一定程度上弥补了国内在生物恐怖医学干预效果评价方面的不足,可用于炭疽生物恐怖应急准备的论证评估,以及作为生物防御能力建设的参考。
从本研究的评估结果可以发现,缩短干预介入延迟时间和提高资源储备量均能减少最终的死亡人数,且前者更重要,提示事件早期侦查预警能力的建设对生物恐怖防御非常关键。从人群发病规律来看,干预策略对峰值时间影响很小,但对峰值人数影响较大,该结果为应对医疗救治高峰的准备提供了参考。
本研究从个体层面进行建模,基于离散事件仿真的方法,考虑了不同个体吸入的炭疽芽孢数量、感染后发展到相应病程阶段的时间以及接受医疗干预的时间等差异,在一定程度上解决了个体之间的异质性问题。但是,个体之间除了存在上述差异以外,其年龄差异、免疫差异以及对治疗方案依从性的差异等也会影响个体的感染概率和医疗干预效果,如何在模型中表述这种更为复杂的个体异质性,是今后研究中需要面对的一个重要挑战。其次,炭疽生物恐怖事件中,个体暴露后在医学干预下的疾病发生、发展以及事件发生后状态队列的人群转移规律,是模拟事件发展和评估事件最终后果的基础。目前相关数据如感染概率、医疗干预后的康复率、各时期的持续时间等主要还是来自于动物实验、体外实验以及对以往事件的回顾分析,提高相关数据、参数的准确性依然是今后相关研究的重点。另外,对于生物事件的应急响应政策、具备的响应能力存在国家和地区差异,将实际情况引入评估方法中将更具现实意义。
| [1] |
BERMAN O, GAVIOUS A. Location of terror response facilities:a game between state and terrorist[J]. Eur J Oper Res, 2007, 177: 1113-1133. DOI:10.1016/j.ejor.2005.12.022 |
| [2] |
BUEHLER J W. Public health response to biological and chemical weapons:WHO guidance[J]. Emerg Infect Dis, 2005, 11: 186-187. |
| [3] |
WEIN L M, CRAFT D L, KAPLAN E H. Emergency response to an anthrax attack[J]. PNAS, 2003, 100: 4346-4351. DOI:10.1073/pnas.0636861100 |
| [4] |
CRAFT D L, WEIN L M, WILKINS A H. Analyzing bioterror response logistics:the case of anthrax[J]. Manag Sci, 2005, 51: 679-694. DOI:10.1287/mnsc.1040.0348 |
| [5] |
WEIN L M, CRAFT D L. Evaluation of public health interventions for anthrax:a report to the Secretary's Council on Public Health Preparedness[J]. Biosecur Bioterror, 2005, 3: 348-356. DOI:10.1089/bsp.2005.3.348 |
| [6] |
JAMROG D C, SHATZ M P, SMITH C. Modeling responses to anthrax and smallpox attacks[J]. Lincoln Lab, 2007, 17: 115-129. |
| [7] |
ZARIC G S, BRAVATA D M, CLEOPHAS HOLTY J E, MCDONALD K M, OWENS D K, BRANDEAU M L. Modeling the logistics of response to anthrax bioterrorism[J]. Med Decis Making, 2008, 28: 332-350. DOI:10.1177/0272989X07312721 |
| [8] |
CHEN W Y, ALAIN G, ANGEL R. Modeling the logistics response to a bioterrorist anthrax attack[J]. Eur J Oper Res, 2016, 254: 458-471. DOI:10.1016/j.ejor.2016.03.052 |
| [9] |
RAINISCH G, MELTZER M I, SHADOMY S, BOWER W A, HUPERT N. Modeling tool for decision support during early days of an anthrax event[J]. Emerg Infect Dis, 2017, 23: 46-55. DOI:10.3201/eid2301.151787 |
| [10] |
BROOKMEYER R, JOHNSON E, BARRY S. Modelling the incubation period of anthrax[J]. Stat Med, 2005, 24: 531-542. DOI:10.1002/(ISSN)1097-0258 |
| [11] |
JAMOLIN K, SALTZMAN J, SCHAEFER D, SERRANO S, SHIM A, SLOANE J. Improving the timeliness and response to an aerosolizedanthrax attack in the metropolitan Washington, D.C. region[Z/OL]. (2013)[2018-10-05]. https://drum.lib.umd.edu/bitstream/handle/1903/13877/.
|
| [12] |
ISUKAPALLI S S, LIOY P J, GEORGOPOULOS P G. Mechanistic modeling of emergency events:assessing the impact of hypothetical releases of anthrax[J]. Risk Anal, 2008, 28: 723-740. DOI:10.1111/risk.2008.28.issue-3 |
| [13] |
杨晔, 曹博, 陈义学. 拉格朗日粒子模型在核事故应急中的开发与应用[J]. 原子能科学技术, 2013(S2): 712-716. |
| [14] |
WILKENING D A. Sverdlovsk revisited:modeling human inhalation anthrax[J]. PNAS, 2006, 103: 7589-7594. DOI:10.1073/pnas.0509551103 |
| [15] |
HENDRICKS K A, WRIGHT M E, SHADOMY S V, BRADLEY J S, MORROW M G, PAVIA A T, et al. Centers for disease control and prevention expert panel meetings on prevention and treatment of anthrax in adults[J/OL]. Emerg Infect Dis, 2014, 20(2). doi: 10.3201/eid2002.130687.
|
| [16] |
HOLTY J E C, BRAVATA D M, LIU H, OLSHEN R A, MCDONALD K M, OWENS D K. Systematic review:a century of inhalational anthrax cases from 1900 to 2005[J]. Ann Intern Med, 2006, 144: 270-280. DOI:10.7326/0003-4819-144-4-200602210-00009 |
| [17] |
U.S. Department of Homeland Security. Target Capabilities List. A companion to the National Preparedness Guidelines[EB/OL]. (2007-09-30)[2018-10-05]. https://www.fema.gov/pdf/government/training/tcl.pdf.htm.
|
| [18] |
HUPERT N, CUOMO J. Computer staffing model for bioterrorism response[EB/OL]. (2005-09-01)[2018-10-05]. http://archive.ahrq.gov/research/biomodel.htm.htm.
|
 2019, Vol. 40
2019, Vol. 40


