近年来,随着人工智能技术的发展,医疗服务机器人得到了广泛应用,其将医疗人员从繁重体力劳动中解放出来,同时也有效节约了医院人力成本[1]。医疗服务机器人在其长距离行进过程中需要实时获得其定位信息[2-5]。常用的服务机器人导航方法包括磁导航、惯性导航、视觉导航等。磁导航可靠性较高,但成本较高且维修困难;惯性导航是服务机器人常用的导航方式,因其会导致累积误差无限增大而不适合长时间精确导航。目前常用的医疗服务机器人导航方式为基于网格的运动统计(grid-based motion statistics,GMS)组合导航方式,这种导航方法虽然稳定性高,但有较大的累积误差[6-7]。基于视觉里程计定位是目前较为新颖的一种医疗服务机器人定位技术[8-10],机器人通过摄像机采集图像特征,根据图像特征和运动约束融合信息进行位姿估计和自主导航[11-12]。随机采样一致性(random sample consensus,RANSAC)算法是常用的视觉特征配准算法之一,但RANSAC算法的误匹配率和复杂度较高。本研究提出了一种基于评分框架的GMS(scoring framework grid-based motion statistics,SF-GMS)特征配准算法,由于运动平滑性使匹配特征点邻域有较多正确匹配对,将正确和错误匹配特征数非线性函数作为评分函数,根据设定阈值确定特征匹配标准。SF-GMS算法与RANSAC算法相比有较好的实时性和特征匹配准确率。
1 基于SF-GMS算法的匹配配准算法 1.1 ORB(oriented FAST and rotated BRIEF)算法[13]ORB算法是一种基于视觉信息的特征点检测与描述算法,其使用FAST(features from accelerated segment test)算法检测某一待测特征点及周围区域内的像素值,该区域一般为圆形区域。同时,ORB算法采用BRIEF(binary robust independent elementary features)算法进行特征点描述,在特征点附近选取若干对随机点,比较每一对随机点的像素大小并进行二进制赋值,然后组合成一个二进制编码,即为特征描述子。根据匹配点与非匹配点的Hamming距离设定阈值,实现匹配。
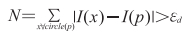
|
式中I(x)表示圆形区域中任一点像素值,I(p)为待检测特征点像素值,εd是设定阈值。若N>εd,则判断此点为特征点。
由于ORB算法建立在FAST特征点检测和BRIEF特征点描述基础上,在保证尺度、旋转不变的前提下,其运算速度可有较大提高。该ORB特征提取算法适用于对称环境或特征点较难获取的复杂环境,如医院走廊、对称病房等,可有效提高特征匹配率,从而提高医疗服务机器人的全局定位精度。
1.2 基于SF-GMS算法的配准算法命题:假设图像序列{Sa, Sb}中各有{n, m}个特征,X={x1, x2, …, xn}是{Sa, Sb}所有特征匹配的集合。那么每个特征匹配对邻域中的特征点数量可作为成功特征匹配率标准。
证明:{Sa, Sb}中特征点邻域表示为{a, b},每个对应有{n, m}个特征。Xi∈X, Xi是邻域{a, b}匹配子集。Si是匹配点邻域度。
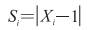
|
可以用二项式分布函数Si近似表示在xi邻域的匹配分值。
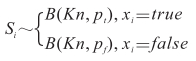
|
其中pt、pf为正确和错误匹配概率,Si整体呈双峰分布,其平均值和标准差分别为
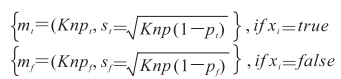
|
其中K为区域中不连接邻域的数量,根据上述公式可量化为一个概率评分标准函数:
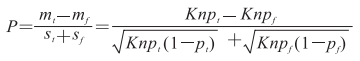
|
从公式可知评价函数P与特征点数量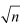
利用实验室场景模拟医疗机器人巡视病房过程,包括室内病房环境和医院走廊对称环境等。分别对特征提取与配准中的比例尺度变化、光照变化、旋转和仿射变化进行实验分析。算法执行流程为:先进行ORB特征点检测,再执行ORB特征点匹配,最后配准,比较SF-GMS与RANSAC算法实验效果。
均取500个特征点,对比SF-GMS与RANSAC算法在同一环境中ORB特征点4种不变性的综合性能。图 1所示为在比例尺度变换(相距4 m)条件下的配准效果,SF-GMS算法的正确配准特征点对数(214对)是RANSAC算法(92对)的2.33倍。图 2所示为在光照变化条件下的配准效果,SF-GMS算法的正确配准对数(118对)是RANSAC算法(90对)的1.3倍。图 3所示为在视角变换(相差水平转角为30°)条件下的配准效果,SF-GMS算法的正确配准对数(365对)是RANSAC算法(283对)的1.29倍。图 4所示为在仿射变换(将目标沿垂直视角偏转20°)条件下的配准效果,SF-GMS算法的正确配准对数(134对)是RANSAC算法(87对)的1.54倍。具体性能分析数据见表 1。与RANSAC算法相比,SF-GMS算法对ORB比例尺度、光照、旋转、仿射4种特征不变特性的匹配正确率分别提高了128%、80%、73%、111%,SF-GMS算法具有更好的配准效果。分析其原因为RANSAC算法从包含大量局外点的数据集中计算参数时迭代次数没有上限,算法对环境变化依赖较高,导致配准率降低。运动平滑性导致匹配特征点邻域有较多匹配点对,但对于特征点邻域中不存在匹配点对时,需要滤掉这些特征点。SF-GMS算法依据特征点邻域中的匹配对数量,具有更高的匹配正确率。

|
图 1 两种算法的比例尺度不变性 Fig 1 Scale invariance of two algorithms A: Scoring framework grid-based motion statistics (SF-GMS); B: Random sample consensus (RANSAC) |

|
图 2 两种算法的光照不变性 Fig 2 Illumination invariance of two algorithms A: Scoring framework grid-based motion statistics (SF-GMS); B: Random sample consensus (RANSAC) |

|
图 3 两种算法的角度旋转不变性 Fig 3 Rotation invariance of two algorithms A: Scoring framework grid-based motion statistics (SF-GMS); B: Random sample consensus (RANSAC) |

|
图 4 两种算法的仿射不变性 Fig 4 Affine invariance of two algorithms A: Scoring framework grid-based motion statistics (SF-GMS); B: Random sample consensus (RANSAC) |
|
|
表 1 SF-GMS与RANSAC的特征匹配性能分析 Tab 1 Performance of feature matching of SF-GMS and RANSAC algorithms |
从匹配时间数据(表 1)可知,SF-GMS算法对4种特征不变性的匹配时间均约为RANSAC算法的25%。这是因为RANSAC算法检测随机点欧式距离,时间复杂度为O(n2);而SF-GMS算法计算特征点间海明距离,时间复杂度为O(n)。因此,SF-GMS算法具有较好的实时性,更适合医疗服务机器人视觉导航的特征匹配过程。
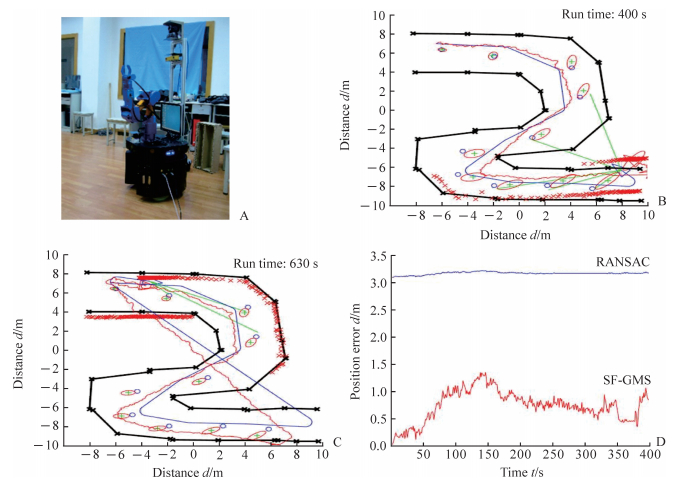
2.2 医院环境下自主导航实验结果分析基于视觉导航的医疗服务机器人特征配准后需重新估计当前时刻位姿,所以特征配准的准确率和实时性将影响自主导航综合性能。采用本实验室MTR服务机器人、Ubuntu14.04操作系统、编程环境openCV3.1.0分析医疗机器人导航定位精度,深入研究SF-GMS算法。图 5A为MTR服务机器人;图 5B为基于SF-GMS算法的自主导航实时界面图,其中黑色边界表示医院走廊墙壁,蓝线表示医疗机器人的设定标准路径,红线表示机器人的实际导航轨迹,蓝色圆圈表示轨迹路点,红色椭圆表示位姿估计可靠性;图 5C为基于RANSAC算法的自主导航实时界面图;图 5D为SF-GMS和RANSAC算法在自主导航过程中与标准路径的x,y方向上的位置误差。SF-GMS算法的位置均值误差为0.74 m;RANSAC算法的位置均值误差为3.17 m。SF-GMS算法的导航误差仅为RANSAC算法的23.34%。医疗服务机器人从起点穿越走廊到达病房指定位置,导航过程中机器人实时避障路径规划,根据特征配准更新当前时刻位姿,实现自主定位和地图更新。机器人采用SF-GMS算法将当前图像特征与地图库中三维路标匹配,根据里程计和特征匹配融合信息实现位姿和地图更新。与RANSAC算法相比,SF-GMS算法具有更好的正确特征配准率,有效减少了自主导航中里程计累积误差,提高了医疗服务机器人自主定位精度。因此,SF-GMS算法可使医疗服务机器人在自主导航中表现出更好的综合性能。
|
图 5 医院环境下的自主导航过程 Fig 5 Autonomous navigation in hospital environment A: MTR service robot; B: Real time interface for SF-GMS algorithm (the black border indicates the hospital corridor wall, the blue line indicates the actual route of the medical robot, the red line indicates the odometer estimated trajectory, the blue circle indicates the three-dimensional road sign, and the red ellipse indicates the pose estimation reliability); C: Real time interface for RANSAC algorithm; D: The position error of the SF-GMS algorithm and the RANSAC algorithm in the autonomous navigation process.SF-GMS: Scoring framework grid-based motion statistics; RANSAC: Random sample consensus |
3 结论
本文提出了一种SF-GMS特征配准算法,通过当前特征图像与地图库中具有三维坐标的路标图像进行特征匹配,实时更新自身位姿和全局地图。与传统RANSAC算法相比,SF-GMS算法在确保自主定位精度的前提下,可有效提高自主导航的实时性,对于提高医疗服务机器人的综合性能具有深远意义。
| [1] |
BEER J M, SMARR C A, CHEN T L, PRAKASH A, MITZNER T L, KEMP C C, et al. The domesticated robot:design guidelines for assisting older adults to age in place[C]//ACM/IEEE International Conference on Human-Robot Interaction. IEEE, 2012:335-342.
|
| [2] |
COMPORT A I, MALIS E, RIVES P. Accurate quadrifocal tracking for robust 3D Visual Odometry[C]//2007 IEEE International Conference on Robotics and Automation, Roma. IEEE, 2007:40-45.
|
| [3] |
FRAUNDORFER F, SCARAMUZZA D. Visual odometry:PartⅡ:matching, robustness, optimization, and applications[J]. IEEE Robot Autom Mag, 2012, 19: 78-90. DOI:10.1109/MRA.2012.2182810 |
| [4] |
NISTER D, NARODITSKY O, BERGEN J. Visual odometry[C/OL]//Computer Vision and Pattern Recognition, 2004. IEEE, 2004:I-652-I-659. doi: 10.1109/CVPR.2004.1315094.
|
| [5] |
彭勃, 周文晖, 刘济林. 基于Harris角点检测的立体视觉里程计[J]. 兵工学报, 2007, 28: 1498-1502. DOI:10.3321/j.issn:1000-1093.2007.12.019 |
| [6] |
BIAN J, LIN W Y, MATSUSHITA Y, YEUNG S K, NGUYEN T D, CHENG M M. GMS:grid-based motion statistics for fast, ultra-robust feature correspondence[C]//IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2017:2828-2837.
|
| [7] |
庞树茂, 黄泽彬, 刘兆周. 医疗机器车避障技术的研究[J]. 中国医药物理学杂志, 2013, 30: 4159-4163. |
| [8] |
SCARAMUZZA D, FRAUNDORFER F. Visual Odometry[Tutorial][J]. IEEE Robot Autom Mag, 2011, 18: 80-92. DOI:10.1109/MRA.2011.943233 |
| [9] |
DISSANAYAKE G, DURRANT-WHYTE H, BAILEY T. A computationally efficient solution to the simultaneous localisation and map building (SLAM) problem[J]. IEEE Trans Ra, 2013, 17: 229-241. |
| [10] |
翟光, 张景瑞, 张尧. 基于共面光标提取的空间目标单目测量技术[J]. 北京理工大学学报, 2013, 33: 1015-1020. DOI:10.3969/j.issn.1001-0645.2013.10.004 |
| [11] |
NOURANI-VATANI N, ROBERTS J, SRINIVASAN M V. Practical visual odometry for car-like vehicles[C]//IEEE International Conference on Robotics and Automation. IEEE, 2009:1411-1417.
|
| [12] |
KIM T, IM Y J. Automatic satellite image registration by combination of matching and random sample consensus[J]. IEEE Trans Geosci Remote, 2003, 41: 1111-1117. DOI:10.1109/TGRS.2003.811994 |
| [13] |
RUBLEE E, RABAUD V, KONOLIGE K, BRADSKI G. ORB:an efficient alternative to SIFT or SURF[C]. Proceedings of the 2011 International Conference on Computer Vision, 2011, 58:2564-2571.
|
 2018, Vol. 39
2018, Vol. 39


