军队在执行作战行动中因失去作业能力而造成的人员损失,称为减员。现代战争中士兵生命尤为宝贵。因此对战争中的减员情况进行科学预测可为制定卫勤保障计划提供科学依据,有助于卫生资源的合理配置,提高卫勤保障针对性和时效性,挽救更多士兵的生命[1-2]。
本研究通过系统动力学模型模拟作战过程,分析红蓝双方交战中目标毁伤并推导战斗减员总数;使用智能体建模方法[3],对系统动力学模型中测算的宏观减员进行拆分,进一步分析每位减员个体的微观伤情信息,通过模拟仿真试验[4]表明:使用系统动力学建模进行作战过程模拟和战斗减员预计可以取得很高的精确度,是研究这类问题有效途径。
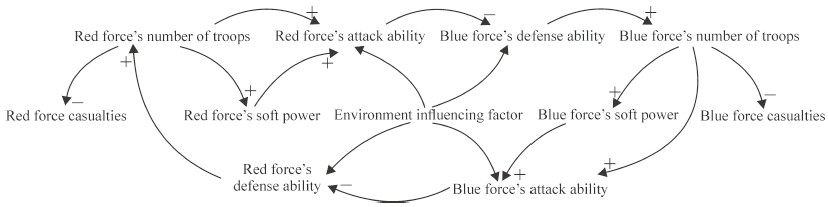
1 方法 1.1 作战过程模拟和战斗减员预计系统动力学模型的建立红蓝双方作战中的整体结构关联和因果关系如图 1所示。基本因果关系是:(1)蓝军进攻——削弱红军防御——红军减员——红军进攻能力降低——降低蓝军的防御压力——蓝军的减员速率降低;(2)红军进攻——削弱蓝军防御——蓝军减员——蓝军进攻能力降低——降低红军防御压力——红军减员速率降低;(3)蓝军防御——抵抗红军进攻——蓝军减员速率降低——蓝军攻击能力衰减减慢;(4)红军防御——抵抗蓝军进攻——红军减员速率降低——红军攻击能力衰减减慢;(5)自然气候、地理环境、士气、训练等影响因素——影响红蓝双方进攻、防御能力。以上5个回路反映了红蓝双方交战过程的基本逻辑关系[5-6]。
|
图 1 红蓝双方交战过程因果回路图 Fig 1 Causal-effect loop diagram of combat process in Red and Blue forces +: Forward direction polarity; -: Negative direction polarity |
1.2 模型参数和方程构造 1.2.1 攻击、防御能力参数测算[7]
主要是红蓝双方各作战群组攻击能力、防御能力的参数计算。计算分为3个步骤:(1)武器性能参数化,攻击能力选取攻击距离、攻击频率、穿甲深度、杀伤半径、命中精度5个指标,防御能力选取装甲厚度、伪装、主动防御、外形尺寸、机动性5个指标,通过文献[8]获取具体数值;(2)参数指数化,即单件武器同类型参数均需按相同标准指数化,保证不同武器之间的攻击、防御能力具有可比性;(3)指数归一化,将衡量武器一种特性的指数化指标,通过绘制雷达图、计算雷达图面积的方法合并为一个基本指数。所有单件装备参数计算完成后,再根据各作战群组武器装备数和作战兵力数进行加权求和,得出红蓝双方各作战群组整体作战效能,并代入模型中相关参数。
1.2.2 作战影响因素参数设定邀请原石家庄、大连陆军学院作战指挥专业8名副高以上职称、有多年军事学教学经验的专家,通过层次分析法确定士气、训练、情报侦察、后勤保障4种影响因素对战斗进程影响的权重。具体方法为邀请专家根据4种影响因素两两之间的重要程度,按照特别重要、一般重要、基本相同、比较不重要、特别不重要5种相互关系评分。将所有专家评分矩阵通过加权几何平均法计算,获得综合判断矩阵,将数据进行整理即可得到上述4种能力影响因素权重[9]。
之后以作战样式为因变量,自然地形和环境气候为自变量,通过专家咨询法量化不同作战条件下自然地形和环境气候对作战过程的影响,并将以上计算结果代入作战影响因素量化子系统。
1.2.3 作战损耗量计算方程构造运用在国际上广泛认可的兰切斯特第二线性律并经过优化调整,计算作战损耗动态变量。用兰切斯特方程构造作战损耗量计算方程有一些局限性,例如将作战当作一个确定性过程建模,没有考虑损耗率系数动态变化情况、武器压制效果、地形影响及兵力的空间分布等,也没有考虑士气、训练等人的因素[10]。本研究将基本的兰切斯特方程作为动态变量引入系统动力学模型,可以较好地解决上述问题,例如在系统动力学模型运行过程中,武器损耗和部队减员实时发生,因此损耗率系数就随着模拟进程和有关存量的变化而变化,有效解决了仅依据兰切斯特方程本身进行损耗计算时损耗率系数无法改变的不足。另外,本研究将各作战群组协同作战情况、各群组交战规则以及士气、训练、地形、气候等影响因素引入模型,实现了对单纯兰切斯特方程的改造和优化。
1.3 基于智能体建模的战伤减员模拟模型设计战斗减员预计模型研究主要解决作战过程中减员在时间和空间中发生的数量问题,战伤减员模型主要是在减员预计研究的基础上分析战斗减员中伤员的结构比例问题。
1.3.1 单智能体设置单智能体用于反映某一类特定类型的伤员结构。以武器类型为自变量,以被打击目标类型为因变量,构建对应关系,每一个对应关系通过一个单智能体表示,每一个单智能体可以调用相关函数、变量、参数和自定义分布,用于描述该单智能体代表的作战群组被敌人不同武器攻击后产生的伤员,并以此构建战伤数据库。
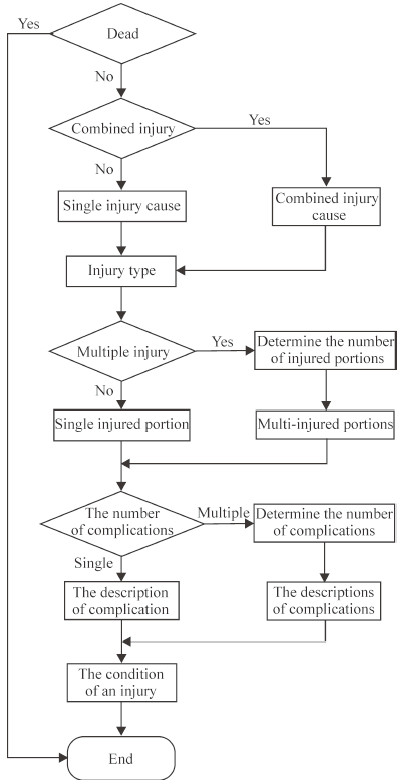
单智能体的运行主要依据战伤发生的逻辑顺序,具体流程如图 2所示:(1)判断是否阵亡。调用“阵亡率”变量,确定减员个体是否阵亡或负伤。(2)伤因信息赋值。当该减员个体为伤员时进行伤因赋值,调用“提取伤因信息”函数,按照战伤数据库中该特定条件下不同伤因发生概率为该伤员随机赋予一个伤因信息。(3)伤型信息赋值。确定伤因后,调用“提取伤型信息”函数,按照该特定条件下不同伤型发生概率为该伤员赋予伤型信息。(4)伤部信息赋值。首先按照“伤部数量”自定义分布中存储的不同数量伤部发生概率为伤员确定伤部数量,之后调用“提取伤部信息”函数,按照确定的伤部数量为该伤员赋予一个或多个伤部信息。(5)并发症信息赋值。首先按照“并发症数量”自定义分布确定伤员并发症数量,然后使用“提取并发症信息”函数按特定概率为该伤员随机赋予一个或多个具体并发症信息。(6)伤势信息赋值。首先确定该伤员伤部数,根据伤部数量确定该伤员轻、中、重、危重4种伤势的具体发生概率。再调用“获取伤势信息”函数,根据伤部数量为该伤员随机赋予一个伤势信息。
|
图 2 战伤发生逻辑关系流程图 Fig 2 Flow chart of war wound occurring |
1.3.2 智能体群设置
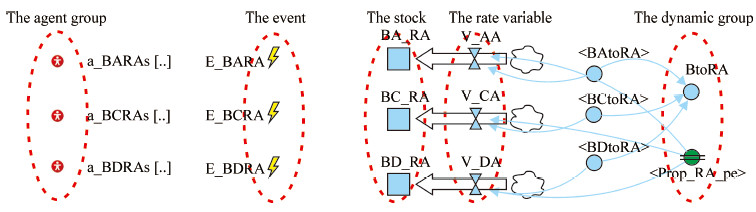
智能体群主要用于在一个具体类型伤员结构下产生批量伤员。模型构建了多个智能体群,代表蓝方不同作战群组对红方各群组攻击造成的战斗减员量,为简化描述。本研究仅以蓝方对红方一个作战群组打击为例简要介绍,如图 3所示。
|
图 3 智能体群示意图(局部) Fig 3 Agent swarm diagrammatic sketch (section) The agent group of a_BARAs/a_BCRAs/a_BDRAs: The group A in Red force's injured individual caused by ground troops/artillery/air force of the Blue force; The event of E_BARA/E_BCRA/E_BDRA: The functions used to convert the casualty stream into the injured individual; The stock of BA_RA/BC_RA/BD_RA: The casualty stream of group A in Red force caused by ground troops/artillery/air force of the Blue force; The rate variable V_AA/V_CA/V_DA: The rate of the casualties of group A in Red force caused by ground troops/artillery/air force of the Blue force; The dynamic variable BAtoRA/BCtoRA/BDtoRA/BtoRA: The combat attrition equation of combat groups in blue force; The dynamic variable Prop_RA_pe: The proportion of soldier and equipment of group A in red force |
图 3中3个存量分别代表蓝方直瞄武器、间瞄火炮和空中打击3种攻击样式对红方一个作战群组进攻后产生的一个连续减员流,由于伤员模拟所需数据应是离散的整数数列,需要构建一个事件对数值进行转换,该事件包含一个计数函数和在特定时刻执行该函数的触发条件,用于时刻监控减员量,当监控的存量中减员量大于智能体群中代表伤员个数的智能体时,进行累加循环,直到代表伤员的智能体个数超过减员存量时停止。此时,就实现了宏观的战斗减员数据流转换为离散的、具体的智能体群中伤员个数,分配到特定的单智能体内后就可以用于伤员具体伤情信息的赋值。
伤员全部信息赋值到每一个具体单智能体内后,可以使用在线谷歌地图或离线地图展示伤员分布,按照红蓝双方速度、距离等参数将红方减员数据投射到地图上。
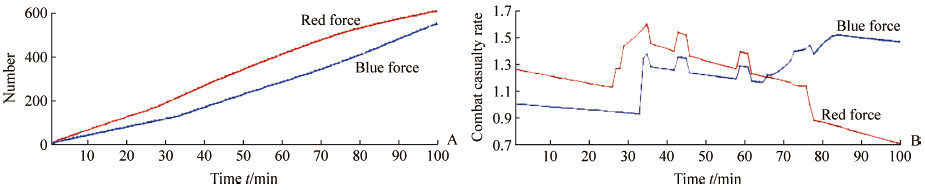
2 结果在模拟前按照作战想定、红蓝双方兵力配置等设置参数,模拟结果基本符合实际情况,红蓝双方总减员数、减员速率如图 4所示。战斗开始阶段,双方火炮和空中力量集中打击对方兵力集结区域,一开始即造成大量减员;减员的第1个波峰发生在红方突破蓝方一线阵地过程中,红蓝双方地面部队首次交火;减员的第2个波峰发生在红方由一线阵地向预备阵地推进阶段;减员的第3个波峰发生在红方突破蓝方预备阵地阶段。自战斗65 min时蓝色折线首次高于红色折线,此时红方预备队加入战斗,导致蓝方防御兵力大量被消灭,蓝方减员速率超过红方。
|
图 4 红蓝双方战斗减员总量(A)和减员速率图(B) Fig 4 Graphs of total number of combat casualties (A) and combat casualty rate (B) in Red and Blue forces |
本次作战红方各作战群组阵亡、轻重中战伤比例如图 5所示。模拟中伤势分布总体特点是轻伤比例降低,重度伤、危重伤比例上升,特别是炮兵群和后方支援保障群重伤和危重伤占战伤减员一半以上。

|
图 5 红方伤员伤势分布图 Fig 5 Histogram of condition of an injury in Red force |
伤员中多发伤占34.2%,伤情变化快、伤情严重、死亡率和休克率高,在战伤救治过程中需要高度关注。在具体伤情中,炸伤占全部伤因总数的25%,由爆炸所造成的冲击伤、烧伤数量分别达到全部伤因总数的15%和10%,比例较高,但是枪伤、刃器伤等数量有所下降;穿透伤占全部伤型总数的21%,比例较高,这主要是由于现代作战爆炸伤产生的破片造成的;胸背部、面部损伤分别占所有伤部总数的21%和13%,比例较高,主要是装甲车辆等受攻击后,在密闭环境中爆炸和燃烧导致伤员内脏器官挫伤和耳骨膜等面部器官冲击伤、烧伤。
通过对这种作战样式进行多次模拟,并与既往作战数据对比分析,结果有很高的一致性,同时也反映出现代战争减员规律较传统作战有以下变化:(1)现代作战进程加快,战斗时间缩短,减员发生密集,散布范围大,战斗减员在整个战场范围内都有可能发生;(2)现代主战武器射程大,交火距离远,轻武器致伤比例降低;(3)机械化部队高速机动,装甲车辆为步兵提供了更好的保护,但是其一旦被击中也会对载员造成严重损伤;(4)空中打击优势作用凸显,使以少胜多成为可能;(5)伤员重伤、危重伤比例大,复合伤、多发伤比例均显著高于既往作战,炸伤以及由于爆炸所造成的冲击伤、烧伤比例增加,而枪弹伤、刃器伤等明显减少。
3 讨论本研究使用系统动力学进行减员预计,优点在于系统动力学中的主要元件非常适合描述作战各个要素,其反馈关系能够很好地反映作战过程中红蓝双方兵力损耗的相互关系;在此基础上使用多智能体仿真方法进行伤员细化的模拟,能够弥补系统动力学仅关注整个系统的宏观分析、难以对系统中具体的个体细致微观描述的缺点。因此,本研究除了提高减员预计的准确性、科学性外,还进一步拓展了减员研究内涵,深入挖掘其时间、空间分布规律以及宏观减员数据中伤员的具体伤情结构,能够为作战时进行快速、精确、高效、全面地预计减员和伤员提供工具和方法,为制定卫勤保障计划、筹措卫勤人力和物力、合理配置卫生资源、有效实施战伤救治提供科学依据,对于提升我军现代战伤救治能力和战时卫勤保障水平具有重要意义。
| [1] | 张鹭鹭. 军队卫生勤务学[M]. 上海: 第二军医大学出版社, 2017: 36-40. |
| [2] | 钟永光. 系统动力学[M]. 北京: 科学出版社, 2012: 15-20. |
| [3] | ILACHINSKI A. 人工战争: 基于多Agent的作战仿真[M]. 张志祥, 高春蓉, 郭福亮, 译. 北京: 电子工业出版社, 2010: 352-355. |
| [4] | 谈彬, 王运斗. 神经网络模型在卫生减员预计方面的初步探讨[J]. 医疗卫生装备, 2004(12): 17–18. DOI: 10.3969/j.issn.1003-8868.2004.12.009 |
| [5] |
邓月仙, 秦超, 李瑞兴, 彭海文, 江雷. 蒙特卡罗模拟在城市进攻战斗减员预计风险分析中的应用[J]. 第二军医大学学报, 2008, 29: 826–828.
DENG Y X, QIN C, LI R X, PENG H W, JIANG L. Monte Carlo Simulation in risk analysis of battle casualty forecasting in urban aggressive military action[J]. Acad J Sec Mil Med Univ, 2008, 29: 826–828. DOI: 10.3321/j.issn:0258-879X.2008.07.027 |
| [6] | 秦超, 陈国良, 李瑞兴, 程旭东, 刘建. 集团军山地进攻作战减员预计模型[J]. 中国管理科学, 2004, 12: 124–127. |
| [7] | 赵定海, 黄玺瑛, 李文生, 谢京龙. 一种通用化的武器装备攻击力指数模型[J]. 装甲兵工程学院学报, 2015, 29: 10–13. |
| [8] | 冯志光. 最新美国陆军武器系统[M]. 北京: 航空工业出版社, 2012: 225-300. |
| [9] | 赵静. 数学建模与数学实验[M]. 北京: 高等教育出版社, 2000: 110-120. |
| [10] | 张明智. 军事定量分析方法[M]. 北京: 国防工业出版社, 2015: 175-180. |
 2018, Vol. 39
2018, Vol. 39


