2. 衡水市疾病预防控制中心, 衡水 053000
2. Center for Disease Control and Prevention of Hengshui, Hengshui 053400, Hebei, China
手足口病是由多种肠道病毒感染引起的传染病,多发于儿童群体[1]。目前研究发现,引起手足口病的病毒种类多达20余种,其中以肠道病毒71型(EV71)[2]和柯萨奇A16型[3]最为常见,前者可引起重症病。手足口病危害大,传播快,其防治任重道远。张家口市地处华北平原,是手足口病多发地区,发病率忽高忽低,所以有必要建立精确可靠的手足口病发病率监测预测系统,为手足口病防治工作奠定基础。
传染病发病率预测模型主要有灰色预测模型[gray forecast model,GM(1,1)][4]、自回归综合移动平均模型(autoregressive integrated moving average model,ARIMA)[5]、支持向量机模型[6]和神经网络(neural network,NN)模型等。GM(1,1)[7]和ARIMA模型[8]通过对数据进行变换处理,形成平稳的时间序列,由于手足口病发病率复杂多变,结果误差较大;支持向量机模型虽然通过核函数可以处理非线性问题,但是对于回归问题参数较多,精度不高;NN[9]模型学习效率较低,难以取得全局最优解。
极端学习机(extreme learning machine,ELM)是一种基于广义NN逼近原理建立的新型NN[10-11],它在随机给定神经元输入权值与偏差的基础上,将传统NN训练问题转化为求解线性方程组,并根据广义逆矩阵理论,以解析方式直接计算出其输出权值的最小二乘解,从而完成网络训练过程。相比于传统NN,ELM由于具有计算原理简单、训练速度快和泛化能力强的优点,是解决时间序列预测问题的有力工具。但其在发病率预测领域极端学习的应用少见报道。本研究将ELM[12]用于手足口病发病率预测,并结合实际数据,以预测误差作为目标函数选取最佳参数进行学习,以期进一步提高模型精度,为张家口市手足口病的预防与控制工作提供参考依据。
1 ELM模型 1.1 ELM回归原理假设训练集为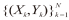
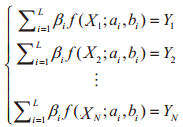
|
(1) |
(1)式中N为训练样本的数量,Xk、Yk分别为第k个训练样本的特征向量和响应值,即输入和输出,βi为连接第i个神经元的输出权值,f(.)为神经元激活函数,αi=[αi1 αi2 ··· αih]为连接第i个神经元的输入权值,bi为第i个神经元的偏差,将(1)式改写为矩阵的形式:
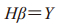
|
(2) |
(2)式中,H为神经元矩阵,Y为输出向量,β为输出权值。其值分别为:

|
由(2)式可知,ELM的训练过程等价于求解线性方程。
1.2 参数的选择ELM模型中涉及的参数有嵌入维数、隐层神经元数量、输入权值、神经元偏置和输出权值。当嵌入维数和隐层神经元数量确定后,输入权值αi和神经元偏置bi在[-1,1]内随机取值,输出权值β利用求取矩阵的MP逆获取最小二乘解。
嵌入维数和隐层神经元数量根据预测误差进行选取,首先确定嵌入维数的取值范围为[1, 10],隐层神经元数量取值范围为[1,150]。其次将训练样本按数量均分为10等份,任意取选9份作为训练数据,1份作为验证数据,依次进行训练,并用验证数据计算预测误差,共进行10次,记录每个参数下的平均预测误差,最后根据平均预测误差的变化规律,选择合适的嵌入维数和隐层神经元数量。
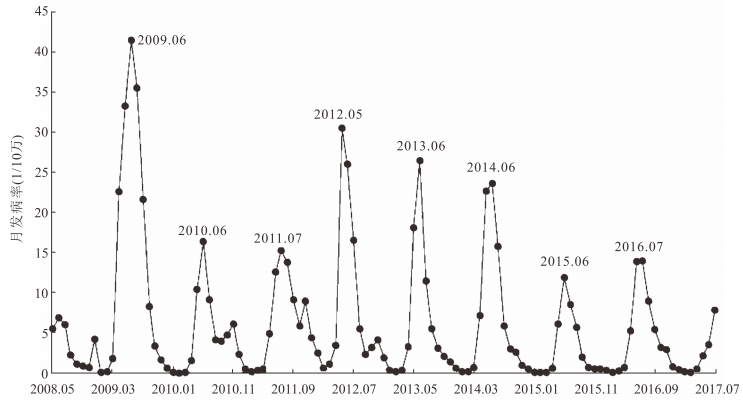
2 资料和方法 2.1 资料来源2008年5月至2017年7月手足口病月发病率数据来自张家口市传染病网络直报系统,人口数据来源于全国第六次人口普查公布结果。见图 1。
|
图 1 张家口市手足口病月发病率时序图 |
2.2 基于数据的模型求解与评价 2.2.1 基于ELM的张家口市手足口病月发病率预测模型
一般来说,嵌入维数和隐层神经元数量越多学习的精度越高,但是这种情况容易出现过拟合现象,严重影响模型的泛化能力。所以在允许的预测误差范围内,选择嵌入维数和隐层神经元数量较少的组合,步骤如下:(1)嵌入维数和神经元数量取值范围设定为[1, 10]×[1, 150],用留一法交叉验证并计算每个参数组合下的平均预测误差。(2)计算最小的平均误差值,记为mine。(3)在平均误差取值范围[1.2×mine,1.3×mine]内寻找嵌入维数h和隐层神经元数量L之和最小的组合,作为最佳的ELM模型参数。
根据上述步骤,选择嵌入维数为5,隐层神经元数量为32。对比的NN模型采用相同的嵌入维数和隐层神经元数量,激活函数采用Sigmoid函数,采用梯度下降法进行训练,学习速率为0.05,最大训练次数为5 000次,设置平均相对误差(mean relative error, MRE)目标界限为0.065。
2.2.2 模型评价指标模型学习效果使用后验差检验方法[13]进行评价,即对模型拟合的残差进行统计学分析。首先计算发病率序列的均值(x)和方差(S0),如下:
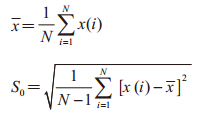
|
其次计算预测残差的均值(Δ)和方差(S1):
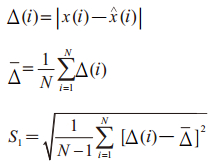
|
由此计算标准差的比值C=S1/S0和决定系数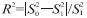
学习的精度高不能说明模型的预测效果好,预测效果主要体现为模型的泛化能力,即对未知数据的适应性。采用MRE对模型预测效果进行评价。MRE越小说明模型预测精度越高。计算公式如下:
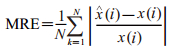
|
式中,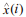
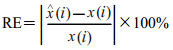
|
用Matlab 2014a软件建立ELM和NN模型,并对学习效果和预测效果进行定量分析。
3 结果 3.1 预测结果对比在构成的手足口病月发病率样本集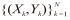

|
图 2 极端学习机模型和神经网络模型训练预测曲线 |
以S1、C、R2和MRE 4个指标对模型进行评价,ELM模型在学习方面性能优于NN模型。ELM模型预测的MRE也优于NN模型。见表 1。
|
|
表 1 极端学习机(ELM)和神经网络(NN)模型对比 |
3.2 多步预测结果对比
多步预测是利用当前张家口市手足口病月发病率数据,逐步向后预测多个月的发病率。本研究将2017年4月至7月的手足口病月发病率作为验证数据,在其余手足口病月发病率数据中选择75%作为学习数据集。多步预测结果如表 2所示。
|
|
表 2 ELM和NN模型用于2017年4月至7月手足口病月发病率多步预测结果对比 |
多步预测效果主要反映了模型的泛化能力和对未知数据的解释能力,由表 2可知ELM的多步预测结果与真实值比较接近。而NN第2步预测的结果偏离真实值较大,后续预测结果与真实值相差较大。从对未知数据的预测能力来看,ELM模型比NN模型较为理想。
4 讨论自2008年以来,张家口市手足口病发病率呈现先上升后下降、波动逐渐规律、最后趋于稳定的状态。众所周知,手足口病发病率受到错综复杂的因素影响,包括流动人口、卫生条件、生活环境、气候等,由于相关资料的检测和收集不充分,又难以判断与手足口病的关系,所以本研究假定错综复杂的影响因素体现在历史数据中,因此对历史发病率建立模型以预测未来数据。
将手足口病月发病率作为时间序列进行处理,因受多因素的影响,数据复杂多变,难以用解析的函数对其进行逼近,所以传统的GM(1,1)和ARIMA模型拟合精度不高,而且建立模型比较复杂,误差较大。而后发展了NN和核函数的方法,逼近非线性函数的能力大幅提高,效果比较显著,但是NN模型采用误差反向传播的机制对模型参数进行求解,隐函数为非线性函数,其导数只在中心值的附近呈现近似的线性关系,并且线性关系的范围会随中心值的不同差异较大,所以选择不同的优化步长对模型参数的求解影响较大,使NN难以收敛或收敛于局部最小解的情况时有发生,在模型建立过程中参数求解过程比较复杂、耗时,且精度没有ELM高。ELM模型本质上为一单隐层NN,继承了NN逼近非线性函数的优点,但其训练机制与NN不同,利用求神经元矩阵的MP逆获取最小二乘解,学习速度快且精度高。
本研究利用留一折的方法计算不同参数下的平均预测误差,依据此误差矩阵获取最佳的嵌入维数和隐层神经元数量,所建立的ELM模型不仅训练结果较好,预测精度也得到了提高。训练精度仅为为NN模型的一半(0.05 vs 0.09),而一步预测精度也比NN高出约70%(0.07 vs 0.12)。从多步预测结果来看预测值与真实值较为接近。
本研究显示,ELM模型适合张家口市手足口病发病率的拟合与预测,这对指导公共卫生人员依据疫情提前做好防控工作并制定有效防控策略具有重大意义。
| [1] | 单宝英. 不同病原所致手足口病临床特征分析[J]. 中国现代医学杂志, 2016, 26: 119–122. |
| [2] | 邵勤, 刁玉巧. EV71感染手足口病患儿血清内皮素-1水平测定及其临床意义[J]. 中国现代医学杂志, 2013, 23: 91–93. |
| [3] | 刘莹莹, 于秋丽, 苏通, 赵文娜, 谢赟, 齐顺祥, 等. 2011-2015年河北省手足口病流行特征及病原特征分析[J]. 中华疾病控制杂志, 2017, 21: 151–155. |
| [4] | 杨永利, 毛赛彩, 薛源, 田翔宇, 施学忠. GM(1, 1)和趋势外推模型在我国艾滋病发病率预测中的应用[J]. 中国卫生统计, 2014, 6: 952–954. |
| [5] | 夏菁, 张华勋, 林文, 裴速建, 孙凌聪, 董小蓉, 等. ARIMA模型在疟疾发病率预测中的应用[J]. 中国血吸虫病防治杂志, 2016, 2: 135–140. |
| [6] | 徐学琴, 王瑾瑾, 马晓梅, 刘颖, 杨梦利, 闰国立, 等. 基于支持向量机模型的河南艾滋病发病率预测[J]. 中国现代医学杂志, 2017, 12: 93–95. |
| [7] | 张倩, 陈超. 改进的GM(1, 1)模型在衡水市乙肝发病率预测中的应用[J]. 现代预防医学, 2017, 44: 1925–1928, 1937. |
| [8] | 杨召, 叶中辉, 赵磊, 薛庆元, 梁淑英, 王重建. ARIMA-BPNN组合预测模型在流感发病率预测中的应用[J]. 中国卫生统计, 2014, 31: 16–18. |
| [9] | 曾海燕, 解合川, 任钦, 张兴裕, 李晓松. 径向基函数神经网络在甲型病毒性肝炎发病率预测中的应用初探[J]. 现代预防医学, 2013, 24: 4489–4492. |
| [10] | HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine:a new learning scheme of feedforward neural networks[J]. Proc Int J Conf Neural Netw, 2004(2): 985–990. |
| [11] | HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1/2/3): 489–501. |
| [12] | 何星, 王宏力, 陆敬辉, 姜伟. 基于优选小波包和ELM的模拟电路故障诊断[J]. 仪器仪表学报, 2013, 34: 2614–2619. |
| [13] | 王永斌, 郑瑶, 柴峰, 李向文, 田珍榛, 袁聚祥. 基于周期分解的ARIMA模型在甲肝发病率预测中的应用[J]. 现代预防医学, 2015, 42: 4225–4229. |
 2018, Vol. 39
2018, Vol. 39


