细菌性痢疾是由不同种类的志贺菌引起的一种肠道感染性疾病，其典型症状包括发热、腹痛、里急后重，以及排含黏液、脓血的稀便等^[1]。在我国，细菌性痢疾给人群的健康带来了巨大的挑战。尽管在过去的10年中细菌性痢疾在我国的发病率和死亡率均呈逐年下降趋势，但其发病率一直居于法定报告传染病的前列。根据全国疾病监测系统报道，2012年全国共有20万例细菌性痢疾患者，年发病率高达15.29/10万^[2]。过去的十几年间，江苏省细菌性痢疾发病率有了较大幅度的下降，但因为流行因素广泛存在，加之耐药现象严重、流行菌型不断变迁，且无有效的菌苗预防，细菌性痢疾仍有小规模暴发的可能性，对其防控仍面临严峻挑战^[3]。近年来对于各种传染病流行规律的研究已经成为热点，尤其是对各种疾病预测方法的研究逐渐受到重视。本研究基于江苏省2004年1月至2016年5月细菌性痢疾发病数据，构建单纯自回归滑动平均(autoregressive integrated moving average，ARIMA)模型与ARIMA和非线性自回归(nonlinear autoregressive，NAR)组合模型(ARIMA-NAR组合模型)来预测细菌性痢疾的发病率，然后比较两种模型的拟合和预测效果，探讨两种模型的可行性，为细菌性痢疾的监测和防治提供依据。

数据资料来源于江苏省卫生和计划生育委员会公布的全省法定报告传染病疫情概况以及胡建利等^[3]公开发表的论文内容。人口资料来自于2004年至2015年江苏省统计年鉴。

采用时间序列分析方法对2004年1月至2016年5月江苏省居民细菌性痢疾的发病率进行分析，其中以2015年3月之前的发病率数据作为拟合样本建立模型，以2015年3月至2016年5月的发病率数据作为预测样本比较预测效果。

利用Stata 12.0软件建立ARIMA模型进行时间序列分析。应用MATLAB R2014a软件中时间序列建模工具构建ARIMA-NAR组合模型，通过实证研究评价2种模型的预测效果。

ARIMA模型是由Box和Jenkins于20世纪70年代初首次提出的用于时间序列分析的方法，该方法能够很好地使用时间序列的过去值和现在值预测未来值^[4]。在ARIMA(p, d, q)×(P, D, Q)_s模型中，AR是自回归，p为自回归阶数；MA为移动平均，q为移动平均阶数，d为差分的次数；P、Q分别为季节性自回归和移动平均阶数，D为季节性差分次数^[4]。

ARIMA模型的建立分为4个基本步骤：(1)数据平稳化和模型识别；(2)参数估计；(3)模型诊断；(4)模型预测。利用偏自相关函数(partial autocorrelation function，PACF)和自相关函数(autocorrelation function，ACF)确定p和q。应用赤池信息准则(Akaike information criterion，AIC)与贝叶斯信息准则(Bayesian information criterion，BIC)比较备选ARIMA模型，AIC与BIC值最小的模型为最优乘积季节ARIMA模型^[4]。

建立ARIMA-NAR组合模型预测发病率的步骤分为3步。第1步，构建单纯ARIMA模型用于线性数据的预测。第2步，单纯ARIMA模型预测产生的残差部分(非线性结构)使用NAR模型进行预测。公式表示如下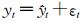：，y_t表示随时间t变化的实际发病率，表示由ARIMA模型预测的发病率，ε_t表示由ARIMA模型预测产生的残差。第3步，由于ε_t通常呈非线性，所以ARIMA模型并不能对其解释，但是NAR模型可以对其进行很好的解释。为了建立模型，将本研究中使用的江苏省细菌性痢疾发病率数据分为75%的训练样本、15%的验证样本和10%的预测样本。训练NAR网络采用LM(Levenberg-Marquardt)训练算法进行神经网络学习。最后通过多次试验确定隐层神经元数和延迟阶数。最终模型性能的选用还要根据误差自相关曲线、时间序列响应图、拟合模型数据以及平均绝对误差(mean absolute error，MAE)、均方误差(mean square error，MSE)和平均绝对百分比误差(mean absolute percentage error，MAPE)来综合判断。决定选择最终模型后再进行模型的预测输出及其检测。

2004年1月至2016年5月江苏省细菌性痢疾发病率(1/10万)的时间序列见图 1A，由图可见细菌性痢疾发病率随着时间呈现下降趋势，同时也呈明显的季节性趋势，每年的12月至次年的2月是发病的低峰期，而7月至8月是发病的高峰期。使用2015年3月之前的发病率数据拟合ARIMA模型，对发病率进行一般差分和季节差分。经过差分后的时间序列曲线如图 1B。尽管发病率数据时间序列经过差分后还有些波动，但相比差分前的数据序列已经实现平稳性，均值在0附近波动，且幅度很小。采用ADF(augmented Dickey-Fuller)单位根检验得到t=-14.708(P＜0.000 1)，拒绝差分后的数据序列存在单位根的假设，提示序列具有良好的平稳性。因此采用乘积季节ARIMA(p, 1, q)×(P, 1, Q)₁₂模型。

图 1 2004年1月至2016年5月江苏省细菌性痢疾逐月发病率(A)、一阶差分和一阶季节性差分的数据序列(B) Fig 1 Monthly incidence of bacillary dysentery (A) and data sequence after a one-order trend difference and one-order seasonal difference in Jiangsu Province between Jan. 2004 and May 2016

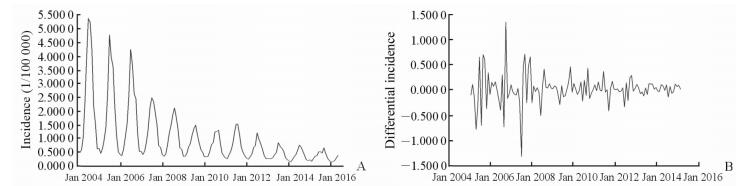
分析差分后发病率时间序列的ACF和PACF(图 2)，可见滞后1期的自相关系数和偏自相关系数都超过了2倍的标准差，除此之外，滞后9期、12期、24期等的自相关系数或偏自相关系数超过了2倍的标准差。提示差分后的序列仍存在季节效应。但是通常P和Q的取值不大于2，而后分别取值构建模型，拟合的有统计学意义的模型为5个(表 1)。在5个备选模型中，ARIMA(1, 1, 1)×(0, 1, 0)₁₂的AIC值和BIC值最小，分别为22.980 6和31.718 5。而且ARIMA(1, 1, 1)×(0, 1, 0)₁₂模型各参数的估计值差异均有统计学意义(P＜0.05)，故最后选取ARIMA(1, 1, 1)×(0, 1, 0)₁₂为最优模型(表 2)。图 3为残差的Bartlett白噪声检验结果，所有的蓝点都在置信区间内，所以残差为白噪声序列。

图 2 细菌性痢疾发病率一阶差分和一阶季节性差分后的序列自相关(A)和偏自相关(B)图 Fig 2 Autocorrelation (A) and partial autocorrelation (B) of bacillary dysentery incidence after a one-order trend difference and one-order seasonal difference MA: Moving average; SE: Standard error

表 1 (Tab 1)

表 1 ARIMA(p, 1, q)×(P, 1, Q)12备选模型 Tab 1 Alternative ARIMA (p, 1, q)×(P, 1, Q)12 models Model AIC BIC ARIMA(0, 1, 2)×(0, 1, 0)12 34.866 3 43.604 2 ARIMA(1, 1, 1)×(0, 1, 0)12 22.980 6 31.718 5 ARIMA(0, 1, 1)×(0, 1, 0)12 38.474 1 44.299 4 ARIMA(1, 1, 0)×(0, 1, 0)12 40.147 4 45.972 7 ARIMA(2, 1, 0)×(1, 1, 1)12 40.856 1 58.332 1  ARIMA: Autoregressive integrated moving average; AIC: Akaike information criterion; BIC: Bayesian information criterion

表 1 ARIMA(p, 1, q)×(P, 1, Q)12备选模型 Tab 1 Alternative ARIMA (p, 1, q)×(P, 1, Q)12 models

表 2 (Tab 2)

表 2 ARIMA(1, 1, 1)×(0, 1, 0)12模型的参数估计 Tab 2 Parameter estimation of ARIMA (1, 1, 1)×(0, 1, 0)12 model Parameter β value t value P value AR(1) 0.58 8.98 < 0.000 1 MA(1) －1.02 －17.16 < 0.000 1  ARIMA: Autoregressive integrated moving average; AR: Autoregressive; MA: Moving average

表 2 ARIMA(1, 1, 1)×(0, 1, 0)12模型的参数估计 Tab 2 Parameter estimation of ARIMA (1, 1, 1)×(0, 1, 0)12 model

图 3 拟合模型残差序列的Bartlett白噪声检验 Fig 3 Cumulative periodogram of Bartlett white-noise test of fitting model residuals series

使用2015年3月之前的发病率数据进行ARIMA-NAR组合模型拟合。以ARIMA(1, 1, 1)×(0, 1, 0)₁₂模型拟合时间序列之后的残差为NAR模型的输入来拟合模型，发现隐层神经元个数为11和延迟阶数为3的NAR模型为最优模型。NAR的预测效果可以通过误差图和误差自相关图进行观察。拟合模型后的残差自相关图显示，只有在延迟阶数为0时残差自相关系数超过95%置信区间，其他自相关系数都在置信区间内，围绕0值波动(图 4)。由此说明NAR模型预测点之间的预测误差相关性是非线性的，相关程度也较小，使得NAR模型的预测点不会因为其上一个预测点的误差较大而产生较大的误差，所以拟合的模型是理想的。图 5所示误差图中竖直方向的黄色线段表示实际值与预测输出值之间的差值，线段越少越短表示NAR模型的预测效果越好。NAR模型的误差图所示的训练样本、验证样本和预测样本中的误差随时间的变化都非常小，由此说明此NAR模型为最优模型。

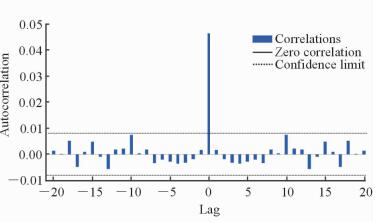
图 4 ARIMA-NAR组合模型拟合后残差的自相关系数的95%置信区间 Fig 4 95% Confidence interval of error autocorrelation of ARIMA-NAR model ARIMA: Autoregressive integrated moving average; NAR: Nonlinear autoregressive

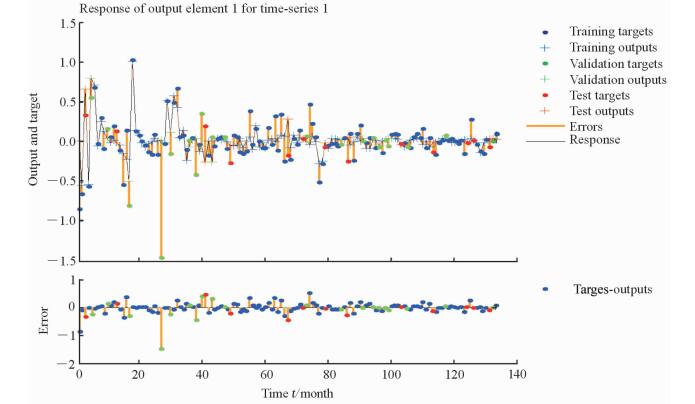
图 5 ARIMA-NAR组合模型拟合后不同样本的残差 Fig 5 Residuals of different samples of ARIMA-NAR model ARIMA: Autoregressive integrated moving average; NAR: Nonlinear autoregressive

为了比较单纯ARIMA模型与ARIMA-NAR组合模型的拟合效果和预测效果，以2015年3月之前的发病率数据作为拟合样本检验2种模型的拟合效果，以2015年3月至2016年5月的发病率数据作为预测样本检验2种模型的预测效果。从图 6可以看出2种模型的拟合值和预测值都非常接近实际值，说明2种模型对细菌性痢疾发病率的时间季节性趋势拟合良好。但是很难直观地从图 6判断2种模型的优劣，所以采用MAE、MSE和MAPE评价2种模型的拟合效果和预测效果(表 3)。不管是在模型拟合阶段还是在模型预测阶段，ARIMA-NAR组合模型的MSE、MAE和MAPE均小于ARIMA模型。可见ARIMA-NAR组合模型对于结果的预测效果更逼近实际值，精度更高，证明此预测模型在预测细菌性痢疾中的应用是有效的。

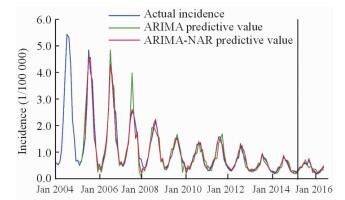
图 6 ARIMA和ARIMA-NAR组合模型的拟合值与实际值 Fig 6 Fitted values simulated by ARIMA and ARIMA-NAR models and actual values ARIMA:Autoregressive integrated moving average; NAR: Nonlinear autoregressive

表 3 (Tab 3)

表 3 ARIMA和ARIMA-NAR模型对细菌性痢疾发病率的预测值(1/10万) Tab 3 Predicting values of ARIMA and ARIMA-NAR models for bacterial dysentery (1/100 000) Model Fitting phase Prediction phase MAE MSE MAPE MAE MSE MAPE ARIMA 0.177 5 0.081 4 0.184 7 0.118 7 0.029 7 0.187 2 ARIMA-NAR 0.094 1 0.029 5 0.104 6 0.058 5 0.0073 0.108 3  ARIMA：Autoregressive integrated moving average; NAR: Nonlinear autoregressive; MAE: Mean absolute error; MSE: Mean square error; MAPE: Mean absolute percentage error

表 3 ARIMA和ARIMA-NAR模型对细菌性痢疾发病率的预测值(1/10万) Tab 3 Predicting values of ARIMA and ARIMA-NAR models for bacterial dysentery (1/100 000)

预测作为一种早期监测的形式，对于传染病的预防控制以及制定有效的控制策略起到了很好的作用。有许多学者应用各种数学模型对细菌性痢疾开展了预测研究^[5-8]，但是由于细菌性痢疾的流行与细菌菌型的变异、耐药菌的出现、有效疫苗的缺少、社会经济因素和自然环境变化等均有密切联系，并且这些影响因素具有复杂性和不确定性^[8]，在现实工作中很难将这些因素的相关资料收集全面，因而导致不能做出准确的预测。时间序列分析法可以很好地克服这些难题，该分析方法充分利用历史数据随时间变化的规律以及数据之间的关系，把各种可能影响疾病的未知因素和已知因素统一蕴含在时间变量中，建立时间序列模型对未来进行预测。

本研究选用江苏省2004年1月至2016年5月细菌性痢疾的发病数据构建了2种模型——单纯ARIMA模型和ARIMA-NAR组合模型。验证结果提示ARIMA模型预测时的误差比拟合时还小，预测效果较好。类似的，国内学者应用ARIMA模型预测的细菌性痢疾发病率与实际值也较为接近，都在预测值的置信区间范围内^[9-11]。这充分体现了ARIMA模型对呈线性结构的数据序列的良好解释能力，但是其对呈非线性结构的数据，如对ARIMA模型拟合时间序列之后的残差解释力极其微弱。刘文东等^[5]尝试应用反向传播(BP)神经网络预测痢疾发病率，其MAE为0.079 2，高于本研究的0.058 5。究其原因可能是由于BP神经网络算法实质上是非线性优化问题的梯度算法，从而忽略掉时间序列数据的线性结构部分。孙小宇等^[6]分别应用温特斯法模型及多层感知器模型预测细菌性痢疾的发病率，其MAPE分别为0.266 7和0.471 7，都明显高于本次研究的MAPE(0.108 3)。GM(Grey model)模型也被学者用来预测细菌性传染病发病率，但是其预测效果要劣于ARIMA模型，可能是由于GM模型更适用于无波动或波动较小的时间序列，ARIMA模型更适用于波动较大的时间序列^[7]。本研究中ARIMA模型拟合时间序列之后的残差呈非线性结构，对于此种数据，人工神经网络对其解释力很强。作为动态神经网络的时间序列预测工具——NAR能够敏锐地捕捉到数据的非线性部分变异。在建立的ARIMA-NAR组合模型中延迟阶数被确定为3时模型最优，这提示某个时间点发病数据的残差依赖于前3个点的值，并且ARIMA-NAR组合模型中，拟合样本和预测样本的误差都比单纯ARIMA模型小。具体表现为：拟合样本的MAE、MSE、MAPE分别下降到0.094 1、0.029 5、0.104 6；预测样本的MAE、MSE、MAPE分别下降到0.058 5、0.007 3、0.108 3。本研究结果提示开发和应用ARIMA-NAR组合模型预测细菌性痢疾是一种有效的方法。

神经网络用于传染病的时间序列预测是近年的研究热点，一些采用神经网络的混合模型如ARIMA-NAR和ARIMA-广义回归神经网络已应用于血吸虫病、出血热和结核病的预测^[12-14]。作为动态神经网络之一的NAR模型对非线性时间序列数据有很好的记忆功能，它的输入包含了网络之前输出的反馈，能准确反映数据时间序列的动态性质，较静态神经网络有更精确的预测性能。当用MATLAB R2014a软件对动态时间序列进行预测时，NAR是一个很好的选择，因为NAR能够实现对训练样本更准确的学习。本研究对数据的建模采用了MATLAB R2014a神经网络时间序列GUI工具箱。GUI工具箱由可视化菜单构成，构建NAR模型只需要通过设定不同的隐层神经元个数和延迟阶数来反复调试确定最终模型，但是具体的预测过程无法解释^[15]。

本研究证实，ARIMA模型与NAR模型结合建立的组合模型对江苏省细菌性痢疾发病趋势的预测效果优于单纯的ARIMA模型。这提示在以后的疾病预测中，应该深入研究各种组合模型的使用价值。但是影响细菌性痢疾疫情的环境和自然因素多是随机的，这将会对模型的稳定性带来影响。另外，不同地区的细菌性痢疾的流行规律很可能不一样，这也为模型的实际应用带来挑战。所以，在构建模型时要因时因地的不断加入新的实际数据进行新拟合，从而实现高精度的动态预测。