2. 上海交通大学医学院附属新华医院口腔科, 上海 200092;
3. 同济大学生命科学与技术学院, 上海 200092
2. Department of Stomatology, Xinhua Hospital, Shanghai Jiaotong University School of Medicine, Shanghai 200092, China;
3. School of Life Sciences and Technology, Tongji University, Shanghai 200092, China
下颌牙列缺失的患者在进行传统下半口义齿修复时常存在固位困难的问题,为解决这一问题,我们通常使用种植体支持式覆盖义齿或固定义齿修复。在相同条件下,无论是在咀嚼效率还是美观舒适方面,种植体支持式固定义齿都具有较大优势。
影响种植体支持式固定义齿设计及效果的因素很多,包括牙槽骨条件、咬合力大小、全身疾病、费用等因素,其中牙槽骨因素最为重要。全口牙列缺失的患者通常伴有不同程度的牙槽骨萎缩,而牙槽骨的萎缩程度对修复体设计具有至关重要的影响。牙槽骨萎缩分为垂直向萎缩和颊舌向萎缩。当牙槽骨颊舌向过度吸收时,如要采用种植体支持式固定义齿修复,则需进行骨移植手术,考虑到无牙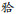
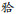
下颌牙列缺失患者1例,男,60岁,下颌骨丰满,前牙区牙槽骨宽度大于6 mm,制作传统下半口义齿,义齿中加入阻射剂(硫酸钡与树脂基托材料的混合比例为1∶3)。将制作完成的下半口义齿戴入患者口中,在锥束计算机断层扫描成像(cone-beam computed tomography, CBCT)下,得到完整的下颌骨及上部义齿的影像图(图 1),包括皮质骨、松质骨、下颌神经管、颏孔以及上部义齿结构;义齿组织面与下颌骨之间的距离为黏膜厚度。将影像数据以DICOM格式导出[5]。
|
图 1 戴有下半口义齿的下颌骨CBCT影像 Fig 1 Cone-beam computed tomography (CBCT) image of edentulous mandible and prosthesis |
将DICOM格式数据导入ITK-SNAP软件(vesion 2.2, 宾夕法尼亚大学, 美国)进行影像处理, 形成三维标准三角语言(STL)表面.修剪STL表面构成骨小梁网格, 经过布尔运算构建并优化颌面部骨骼模型、无牙颌模型、下半口义齿模型, 将输出数据传送到HyperMesh 10.0软件中, 最后形成下颌骨基准模型及上部义齿结构模型(图 2).下颌骨基准模型包括皮质骨和松质骨; 下半口模型进行颊舌侧的基托边缘修整, 保留义齿及少量基托, 作为上部固定义齿模型.
|
图 2 下颌骨(A)以及上部义齿(B)的三维有限元模型 Fig 2 Three-dimensional finite element model of edentulous mandible (A) and prosthesis (B) |
1.2 种植体模型
种植体采用柱形种植体外观,直径4.1 mm,长10 mm (ITI, SW)。根据种植体外形数据应用HyperMesh 10.0软件建立种植体模型。在本实验中忽略种植体螺纹。
1.3 建立不同垂直高度的无牙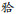
在下颌骨基准模型上,通过牙槽嵴顶下方间隔取像的方法,将牙槽嵴顶平面下移0、5、10、15 mm,形成4个不同程度下颌骨垂直高度的无牙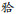
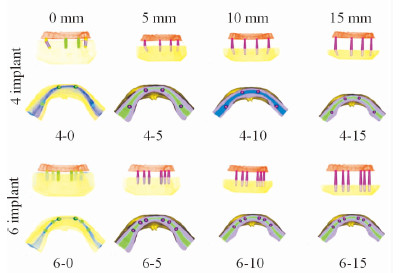
下颌三维模型分别采用以下两种设计模式,应用HyperMesh 10.0软件,在4个不同垂直高度无牙下颌模型上按以下两种设计模式装配种植体和上部义齿。模式1(6-种植体模型):颏孔前6枚相互平行的种植体,支持12颗人造牙的固定桥修复体,表示为模型6-0、6-5、6-10、6-15;模式2(4-种植体模型):颏孔前4枚种植体,两末端种植体向远中倾斜30°,支持12颗人造牙的固定桥修复体,表示为模型4-0、4-5、4-10、4-15。共建立8个三维有限元分析模型(图 3)。
1.5 无牙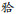
将模型中下颌骨、种植体和上部结构均考虑为连续、均质、各向同性的线弹性材料。弹性模量及泊松比[6-8]见表 1,分别对下颌骨骨皮质与骨松质进行材料赋值,材料变形为小变形,种植体与骨界面为100%骨性结合,加载不发生相对滑动。边界条件:在下颌骨双侧升支后缘及下颌骨下缘咀嚼肌附丽区给予刚性约束,阻止下颌骨的刚体移动[9-11]。加载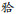
|
图 3
无牙 |
|
|
表 1 下颌骨有限元模型各结构的弹性模量及泊松比 Tab 1 Young's modulus and Poisson's ratio assigned to the mandible model components |
2 结果
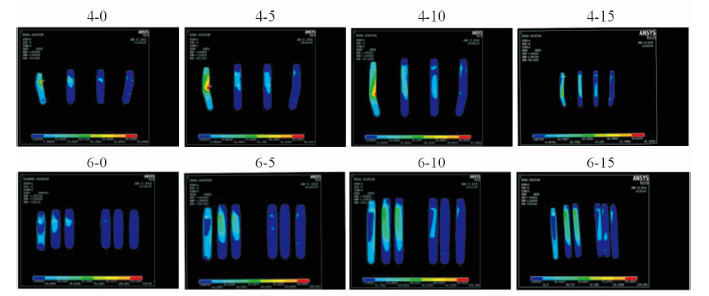
在相同的加载条件下,种植体有限元模型应力云图(图 4)显示,8个模型中越靠近加载侧的种植体(R5)承受的应力越大;种植体的最大应力值位于种植体颈部。
两组8个模型靠近加载侧种植体的最大应力值分布(表 2)显示,4-种植体组,模型4-0、4-5、4-10、4-15最大应力值分别为43.76、40.12、44.26、49.06 MPa;6-种植体组,模型6-0、6-5、6-10、6-15的最大应力值在83.13、80.62、88.88、109.64 MPa;6-种植体组的最大应力值是4-种植体组的2倍,显著大于4-种植体组。
两组模型中,种植体最大应力值在下颌骨垂直高度降低5 mm时表现为最低,随着下颌骨垂直高度的降低,应力逐渐增大;降低0 mm时的最大应力值要大于降低5 mm时。
|
图 4 8个有限元模型的种植体应力云图 Fig 4 The von Mises stress distribution (in MPa) within implants (8 models) |
|
|
表 2 R5种植体颈部最大应力值 Tab 2 Maximum stress of implant neck of R5 |
3 讨论
本实验模拟了牙槽骨不同程度萎缩的下颌骨模型,比较了两种修复设计方案对种植体应力分布的影响。
对于下颌无牙
对于种植体冠根比的研究目前存有较大分歧。文献报道,随着冠根比的增加,种植体周围特别是种植体颈部的应力增加;但也有报道短种植体支持的固定义齿修复也能获得良好的临床效果[10-11]。本实验设定的条件是,当下颌骨垂直高度下降时,垂直距离保持不变,冠根比例随之增加。在下颌骨垂直高度下降5~15 mm范围内,4-种植体组和6-种植体组的种植体颈部应力均随着下颌骨垂直高度下降而增加,表明随着冠根比的增加,从加载点到种植体颈部的力臂增加,导致种植体颈部应力增加。而对于基准模型种植体颈部应力略高于下颌骨垂直高度降低5 mm组的现象,分析其原因可能是加载负荷通过上部义齿结构直接作用于种植体的同时,上部结构材料对负载也有一定的吸收和缓冲的作用,当在力臂较短的情况下,此结构上部结构对于负载的吸收或缓冲作用最小,因而加载在种植体上的负载就相对较大,所以基准模型虽然冠根比较小,却表现出较大的应力。随着基台高度的增加,上部结构吸收负荷的影响小于力臂长度增加的影响,冠根比因素起了主导作用。因此,种植体颈部应力表现出随着冠根比增大而逐渐增大的规律,但其变化是非线性的,这也从另一角度证实了上部结构吸收负荷这一因素的存在[18]。综上所述,本实验显示下颌骨垂直高度下降5 mm时,种植体应力分布更加合理。从临床角度看,在下颌骨有适当萎缩的情况下,一方面可以增加口腔内的垂直修复空间,另一方面也可以使种植体应力分布更加合理,延长种植体的寿命。
咬合力与种植义齿支持结构的稳定性密切相关,人的咬合力存在相当大的差异,咬合力大的人需要更加坚强的支持结构。Correa等[19]测定种植体支持的无牙颌修复体平均最大咬合力前牙区为166 N,磨牙区为240~248 N,前磨牙区为178~182 N。本实验采用单侧施加负荷的方式,加载力为250 N,旨在研究在异常极端咬合情况下,种植体是否会出现破坏性的应力。实验结果显示,4-种植体组的最大应力值为49.06 MPa,6-种植体组的最大应力值为109.64 MPa。而种植体钛金属的抗压强度与抗拉强度均为616 MPa,疲劳强度为364 MPa[20]。因此无论是4-种植体组还是6-种植体组,随着下颌骨垂直高度的下降,虽然种植体颈部应力增加,但并未出现破坏性应力。上述结果说明两种下颌骨种植体支持的固定义齿修复方式都是可行的,但从两组种植体的应力值来看,4-种植体的设计方案更加合理。
实验中,在相同加载条件下,各模型最大的应力均集中在距离加载点最近的种植体上,而且最大应力值均集中在舌侧区。从理论上分析,由于牙槽骨的结构在颊舌向具有非对称性,颊侧皮质骨密度和厚度都要大于舌侧,所以种植体周围骨应力分布在颊侧和舌侧也有明显不同。这种差异随骨密度的降低被明显放大,加剧了一侧的应力集中度。在咬合力作用下,种植体必然向刚度相对低的一侧倾斜,轴向加载就转化为力矩作用。一侧骨密度越低,倾斜程度加大,力矩作用就更加明显。因此,应力在种植体颈部集中的程度就会加剧[21-22]。
在临床种植体支持的下颌半口义齿病例中,松动或者中央螺栓断裂的情况往往出现在远端的种植体。本实验结果发现在加载单一垂直力的情况下,所有的模型组的最大应力值都表现在远端的种植体上,而且集中于颈部皮质骨区域。皮质骨弹性模量远大于松质骨。在相同的形变位移时,弹性模量越大,应力就越大,颈部皮质骨就可能发生吸收,从而导致临床种植体松动[23]。但本实验中加载力只有垂直向,没有考虑侧向力,且实验只能有条件地模拟临床情况,在现实条件下咬合力情况更加复杂。牙槽骨吸收的原因也很复杂,其中的力学机制还有待进一步深入研究。
本实验采用逆向工程法建立了完整的下颌骨、固定义齿、种植体模型,相比传统方法得到更多的细节以及复杂的几何结构,该模型可模拟临床情况,采用三维有限元方法进行应力分析研究。三维有限元方法具有很多优点,有限元是目前最成功建立仿生数学模型的方法之一,可利用其对结构、形状、载荷和材料力学性能等极其复杂的构建进行应力分析,并已广泛应用于口腔生物力学研究领域[20]。但三维有限元法也有其局限性,比如限定所有的修复材料以及下颌骨均为各向同性的线弹性材料。这与临床实际情况有偏差,而且在实际生活中,义齿的受力情况复杂。因此,本实验中应力的绝对数值不是研究关注的重点,只是一个参考。本研究所关注的是各个分析模型应力间的相对数值,以此作为选择两种修复方案的参考[24]。
综上所述,4-种植体和6-种植体支持的无牙颌固定义齿在相对极端的载荷下均未对种植体产生破坏性应力,4-种植体具有更加合理的应力分布;随着下颌骨垂直高度的下降,种植体周围的应力改变有一定规律,其中下颌骨垂直高度降低5 mm组应力最小,说明适当降低牙槽骨高度有利于种植体应力更加合理的分布。
| [1] | BATENBURG R H, MEIJER H J, RAGHOEBAR G M, VISSINK A. Treatment concept for mandibular overdentures supported by endosseous implants:a literature review[J]. Int J Oral Maxillofac Implants , 1998, 13 :539–545. |
| [2] | VISSER A, RAGHOEBAR G M, MEIJER H J, BATENBURG R H, VISSINK A. Mandibular overdentures supported by two or four endosseous implants. A 5-year prospective study[J]. Clin Oral Implants Res , 2005, 16 :19–25. |
| [3] | CHEE W, JIVRAJ S. Treatment planning of the edentulous mandible[J]. Br Dent J , 2006, 201 :337–347. DOI:10.1038/sj.bdj.4814041 |
| [4] | SALEH SABER F, GHASEMI S, KOODARYAN R, BABALOO A, ABOLFAZLI N. The comparison of stress distribution with different implant numbers and inclination angles in all-on-four and conventional methods in maxilla:a finite element analysis[J]. J Dent Res Dent Clin Dent Prospects , 2015, 9 :246–253. DOI:10.15171/joddd.2015.044 |
| [5] | DEVOCHT J W, GOEL V K, ZEITLER D L, LEW D. Experimental validation of a finite element model of the temporomandibular joint[J]. J Oral Maxillofac Surg , 2001, 59 :775–778. DOI:10.1053/joms.2001.24292 |
| [6] | HUANG H L, CHANG C H, HSU J T, FALLGATTER A M, KO C C. Comparison of implant body designs and threaded designs of dental implants:a 3-dimensional finite element analysis[J]. Int J Oral Maxillofac Implants , 2007, 22 :551–562. |
| [7] | O'BRIEN W J. Dental materials and their selection. 2nd ed. Chicago:Quintessence[M]. 2002 . |
| [8] | YANG H S, LANG L A, MOLINA A, FELTON D A. The effects of dowel design and load direction on dowel-and-core restorations[J]. J Prosthet Dent , 2001, 85 :558–567. DOI:10.1067/mpr.2001.115504 |
| [9] | CRUZ M, LOURENÇO A F, TOLEDO E M, DA SILVA BARRA L P, DE CASTRO LEMONGE A C, WASSALL T. Finite element stress analysis of cuneiform and cylindrical threaded implant geometries[J]. Technol Health Care , 2006, 14 :421–438. |
| [10] | CRUZ M, WASSALL T, TOLEDO E M, BARRA L P, LEMONGE A C. Three-dimensional finite element stress analysis of a cuneiform-geometry implant[J]. Int J Oral Maxillofac Implants , 2003, 18 :675–684. |
| [11] | CRUZ M, WASSALL T, TOLEDO E M, DA SILVA BARRA L P, CRUZ S. Finite element stress analysis of dental prostheses supported by straight and angled implants[J]. Int J Oral Maxillofac Implants , 2009, 24 :391–403. |
| [12] | SANTOS L S, ROSSI A C, FREIRE A R, MATOSO R I, CARIA P H, PRADO F B. Finite-element analysis of 3 situations of trauma in the human edentulous mandible[J]. J Oral Maxillofac Surg , 2015, 73 :683–691. DOI:10.1016/j.joms.2014.10.014 |
| [13] | MALHOTRA A O, PADMANABHAN T V, MOHAMED K, NATARAJAN S, ELAVIA U. Load transfer in tilted implants with varying cantilever lengths in an all-on-four situation[J]. Aust Dent J , 2012, 57 :440–445. DOI:10.1111/adj.12002 |
| [14] | TAKAHASHI T, SHIMAMURA I, SAKURAI K. Influence of number and inclination angle of implants on stress distribution in mandibular cortical bone with All-on-four Concept[J]. J Prosthodont Res , 2010, 54 :179–184. DOI:10.1016/j.jpor.2010.04.004 |
| [15] | BEVILACQUA M, TEALDO T, MENINI M, PERA F, MOSSOLOV A, DRAGO C, et al. The influence of cantilever length and implant inclination on stress distribution in maxillary implant-supported fixed dentures[J]. J Prosthet Dent , 2010, 105 :5–13. |
| [16] | BONNET A S, POSTAIRE M, LIPINSKI P. Biomechanical study of mandible bone supporting a four-implant retained bridge finite element analysis of the influence of bone anisotropy and foodstuff position[J]. Med Eng Phys , 2009, 31 :806–815. DOI:10.1016/j.medengphy.2009.03.004 |
| [17] | BEVILACQUA M, TEALDO T, MENINI M, PERA F, MOSSOLOV A, DRAGO C, et al. The influence of cantilever length and implant inclination on stress distribution in maxillary implant supported fixed dentures[J]. J Prosthet Dent , 2010, 105 :5–13. |
| [18] | AKÇA K, AKKOCAOGLU M, CÖMERT A, TEKDEMIR I, CEHRELI M C. Bone strains around immediately loaded implants supporting mandibular overdentures in human cadavers[J]. Int J Oral Maxillofac Implants , 2007, 22 :101–109. |
| [19] | CORREA S, IVANCIK J, ISAZA J F, NARANJO M. Evaluation of the structural behavior of three and four implant-supported fixed prosthetic restorations by finite element analysis[J]. J Prosthodont Res , 2012, 56 :110–119. DOI:10.1016/j.jpor.2011.07.001 |
| [20] | VAN STADEN R C, GUAN H, LOO Y C. Application of the finite element method in dental implant research[J]. Computer Methods Biomech Biomed Engin , 2006, 9 :257–270. DOI:10.1080/10255840600837074 |
| [21] | TEPPER G, HAAS R, ZECHNER W, KRACH W, WATZEK G. Three dimensional finite element analysis of implant stability in the atrophic posterior maxilla:a mathematical study of the sinus floor augmentation[J]. Clin Oral Implants Res , 2002, 13 :657–665. DOI:10.1034/j.1600-0501.2002.130613.x |
| [22] | SERTGÖZ A, GVVENER S. Finite element analysis of the effect of cantilever and implant length on stress distribution in an implant-supported prosthesis[J]. J Prosthet Dent , 1996, 76 :165–169. DOI:10.1016/S0022-3913(96)90301-7 |
| [23] | GENG J P, TAN K B, LIU G R. Application of finite analysis in implant dentistry:a review of literature[J]. J Prosthet Dent , 2001, 85 :585–598. DOI:10.1067/mpr.2001.115251 |
| [24] | LIU J, PAN S, DONG J, MO Z, FAN Y, FENG H. Influence of implant number on the biomechanical behavior of mandibular implant-retained/supported overdentures:a three-dimensional finite element analysis[J]. J Dent , 2013, 41 :241–249. DOI:10.1016/j.jdent.2012.11.008 |
 2016, Vol. 37
2016, Vol. 37


