2. 成都军区总医院药剂科, 成都 610083;
3. 第二军医大学基础部数理教研室, 上海 200433;
4. 第二军医大学训练部信息化办公室, 上海 200433;
5. 解放军309医院全军结核病研究所, 北京 100091
2. Department of Pharmacy, General Hospital, PLA Chengdu Military Area Command, Chengdu 610083, Sichuan, China;
3. Department of Mathematics & Physics, College of Basic Sciences, Second Military Medical University, Shanghai 200433, China;
4. Office of Informatization, Division of Training, Second Military Medical University, Shanghai 200433, China;
5. Institute for Tuberculosis Research, No. 309 Hospital of PLA, Beijing 100091, China
在人们日益受到新旧传染病双重威胁的今天,传染病预测预警工作愈加受到重视。自1928年Reed和Forst共同提出Reed2 Forst模型,1929年Soper 用差分方程提出一种麻疹流行的确定模型以来,越来越多的研究者开始关注人群疾病的预测研究,数学模型在疾病预测中的应用为疾病控制提供了一个很好的指导[1]。在肺结核发病率的预测中,数学模型起着极其重要的作用,通过建立适当的数学模型对其流行趋势进行预测,以便政府有关部门可以及时采取有效措施,减小其危害。目前有多种数学模型被应用于传染病发病率预测,如时间序列模型、神经网络模型、灰色预测模型、回归模型等等。本研究以我国肺结核疫情资料为例,根据逐月发病率特点选择时间序列模型中自回归移动平均 (autoregressive integrated moving average,ARIMA ) 模型和神经网络模型中广义回归神经网络 (generalized regression neural network,GRNN) 模型来进行肺结核发病率预测,比较两个常用模型对于肺结核发病率的预测性能,为我国肺结核的监测和防治工作提供科学依据。
1 资料和方法 1.1 数据来源数据资料来源于中华人民共和国国家卫生和计划生育委员会发布的2004年1月至2013年12月的全国法定传染病疫情概况以及国家统计局发布的2004—2013年人口统计资料。
1.2 ARIMA模型[2, 3, 4, 5, 6, 7]ARIMA模型是将自回归和移动平均过程整合起来的综合模型。该模型将预测对象随时间推移而形成的数据序列视为1个随机序列,除去个别偶然因素影响观察值外,时间序列是一组依赖于时间t的随机变量。完整的ARIMA过程包括模型的识别、模型参数估计、模型的诊断与预测3个步骤。在建模过程中,这3个步骤是循环往复的过程,需要根据参数估计和拟合效果调整模型的形式。通常“最优”模型是那些参数估计具有显著性、拟合效果较好、参数个数最少的模型。
1.3 GRNN模型[8, 9, 10, 11, 12, 13]GRNN 模型是由美国学者Donald F. Specht在1991年提出的,利用径向基神经元和线性神经元建立,是径向基函数RBF神经网络的一个分支。GRNN具有很好的柔性网络结构以及很高的容错性和鲁棒性,适用于解决非线性问题。GRNN在逼近能力和学习速度方面比rbe更优,网络最后将收敛于样本量集聚较多的优化回归面上。在样本数据较少时,预测效果较好。
在Matlab中可以采取以下步骤建立RBF网络:(1)训练样本:根据需要建立训练的样本集对网络进行训练,使误差达到预定值。这只需调用Matlab 7.1神经网络工具箱中的newgrnn函数即可。(2)预测:对新的输入向量使用sim函数,即可得到相应的输出数据,即预测值。
1.4 统计学处理本研究应用Excel软件记录原始数据和模型预测结果;应用Eviews7.0.0 .1 实现ARIMA模型的参数估计、模型拟合及其检验;应用Matlab 7.1神经网络工具箱建立GRNN模型。
2 结 果 2.1 疫情特征我国2004—2012年肺结核平均月发病病例数约为117 711例,年平均发病率约为81.26/10万,年环比发展速度分别为:29.0%、-10.5%、2.7%、0.0%、-8.4%、-8.4%、-4.3%、-0.7%,呈现出平缓的波浪式下降趋势。由此看出我国对肺结核的防治工作取得了可喜的成绩,但是肺结核的防治现状仍然非常严峻,2001—2014年我国肺结核报告发病率及病死率始终位居全国甲、乙类传染病发病率及病死率排序的前3位,因此肺结核仍然是高发传染病之一,在肺结核的防治工作中,发病率的预测有着重要的指导意义。
由图 1可见,2005—2013年肺结核发病病例数在4—7月出现高峰,1—3月出现低谷,呈现出明显的季节周期性。
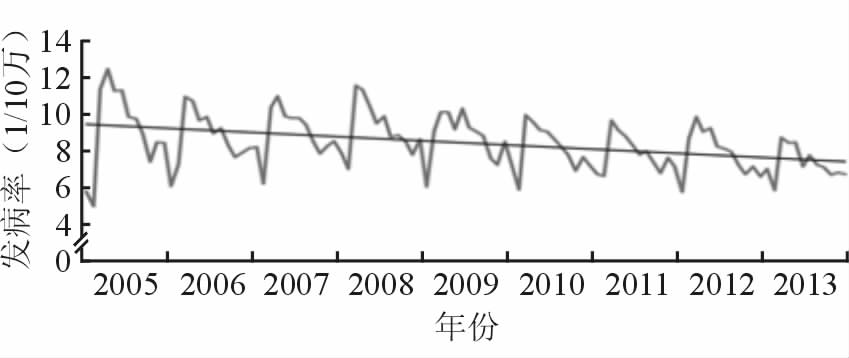
|
图 1 2005—2013年我国肺结核月发病率序列图 |
利用乘积季节ARIMA(p,d,q)×(P,D,Q)s模型对我国2004年1月至2012年12月的肺结核逐月发病率进行拟合,建模步骤如下:(1)经过对备选模型反复定阶后进行参数估计;(2)白噪声检验:模型残差序列必须是白噪声序列;(3)拟合优度比较:确定模型优劣的常用方法有赤池信息准则 (akaike information criterion,AIC)、贝叶斯信息准则(schwartz bayesian criteria,SBC),AIC和SBC值最低的模型为最优模型(表 1);(4)预测结果比较:对预测结果的考察,常用的指标有以下4个:误差均方根 (root mean squared error,RMSE)、绝对误差平均 (mean absolute error,MAE)、相对误差绝对值平均(mean absolute percentage error,MAPE)、Theil不等系数 (Theil inequality coefficient,TIC)。指标数值越低说明预测精度越高(表 2);(5)找到最优拟合模型并将预测结果与2013年1月至12月肺结核发病率数据进行比较(图 2)。最终得到模型ARIMA(2,0,2)×(0,1,1)12,其拟合函数为:
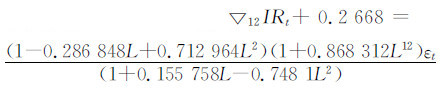
其中IRt是发病率,∇12表示滞后期为12的一阶差分,∇12IRt=IRt-IRt-12,Ls是滞后算子,Lsεt=εt-s,残差序列是白噪声序列,AIC=1.926,SBC=2.088。
|
|
表 1 ARIMA备选模型参数的比较 |
|
|
表 2 ARIMA备选模型样本外动态预测结果的比较 |

|
图 2 ARIMA最优备选模型对2013年肺结核月发病率的动态预测拟合图 ARIMA:自回归移动平均;* 发病率; IRF:发病率预测值; SE:标准差 |
用2004—2012年每年12个月一共108个发病率数据作为训练样本,用前一年12个月的发病率作为网络的输入,用后一年12个月的发病率作为输出,训练网络(不同网络,数据的输入和输出稍有不同)。然后根据训练出来的网络,用2012年12个月的发病率作为输入,预测2013年12个月的发病率。
用matlab命令net4=newgrnn(x1,y1,spread(i))训练该网络,其中x1的每一列分别是2004—2011年每年12个月的发病率,y1的每一列是2005—2012年的每年12个月的发病率。对于spread的不同值,训练网络的预测结果曲线见图 3(为了绘图方便,在模型参数spread选择阶段,我们并未将MAPE指标乘以常数100)。
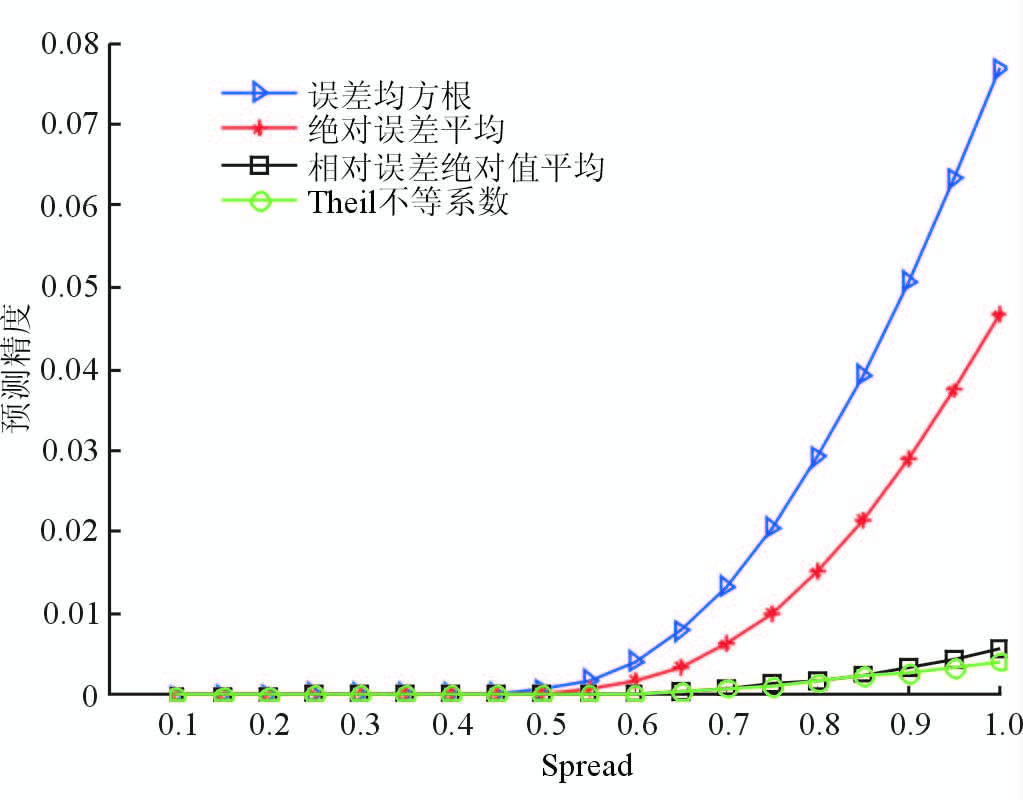
|
图 3 训练网络预测精度与网络参数spread取值之间的关系 |
根据图 3的训练结果,网络参数spread的取值越小越好,因此,我们可以选择最小值0.1作为该网络的spread值。对应于这个参数值,训练样本内预测可以做到零误差。见图 4。
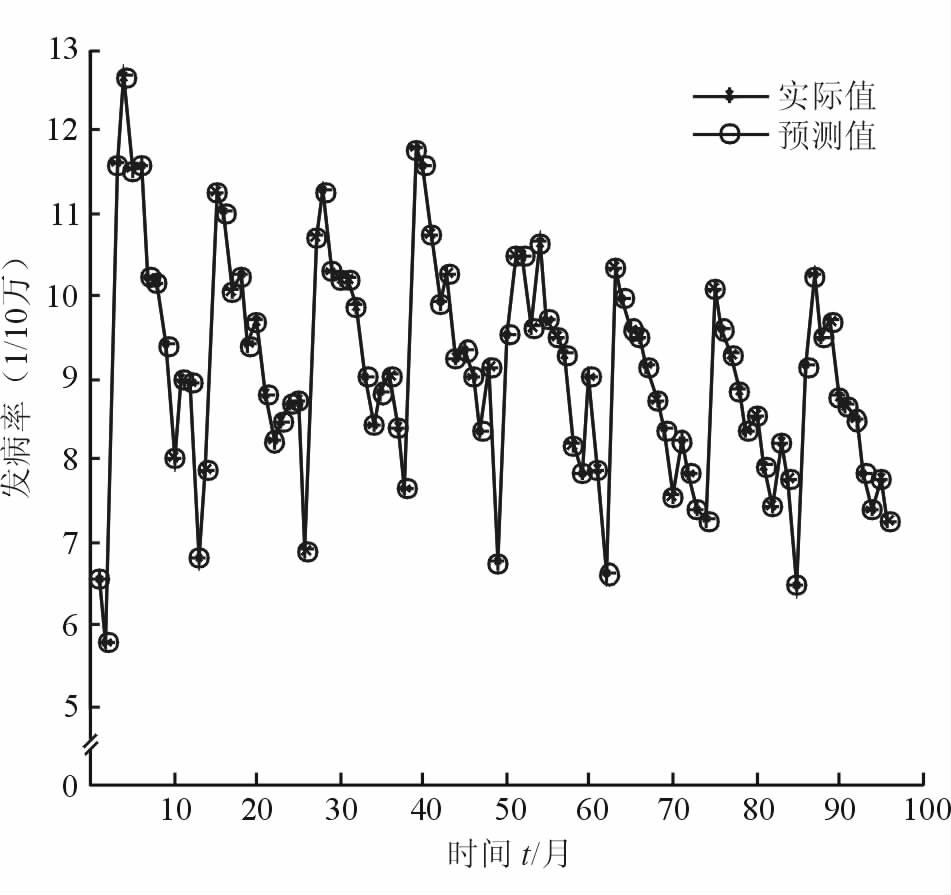
|
图 4 训练样本内预测图 |
用matlab命令sim(net4,x2)预测2013年每个月发病率。输入2012年每个月的发病率x2,x2=[6.491 2,9.158 1,10.242 2,9.503 6,9.693 7,8.769 3,8.667 3,8.494 5,7.842 3,7.392 0,7.774 1,7.260 2],对应于参数spread=0.1,2013年发病率预测结果见图 5。
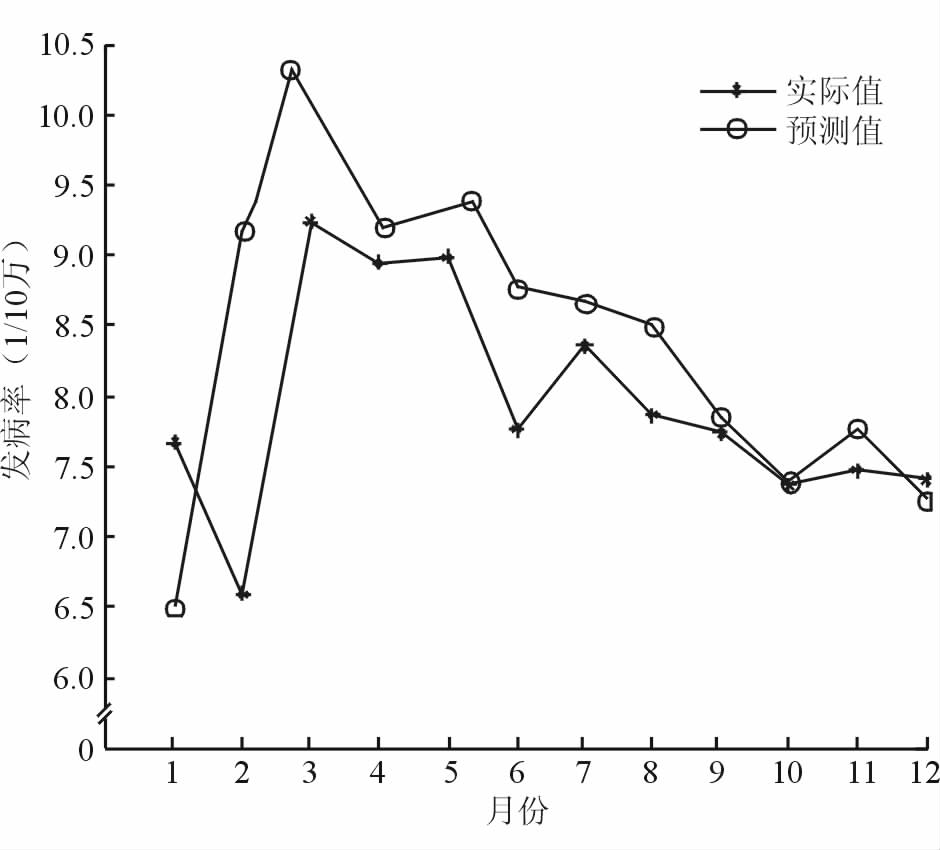
|
图 5 GRNN模型对2013年肺结核月发病率的预测拟合图 GRNN:广义回归神经网络 |
TIC的取值介于0和1之间,数值越小表示拟合程度越高。本研究中指标MAPE乘了一个常数100,是为了与Eviews软件中这一指标的计算相一致。GRNN(spread=0.1)模型的RMSE是0.979,MAE是0.715,MAPE是9.356,TIC是0.059。ARIMA(2,0,2)×(0,1,1)12模型的RMSE是0.538,MAE是0.417,MAPE是5.351,TIC是0.034。结果说明ARIMA模型对我国2013年肺结核逐月发病率的拟合程度优于GRNN模型,ARIMA模型相对误差绝对值仅为GRNN模型的57.19%,提示ARIMA预测模型更适合用于我国肺结核病发病率的预测。
3 讨 论肺结核发病预测研究可以及早发现肺结核发展趋势,为深入开展疾病的预警奠定基础,预测模型可以把肺结核流行趋势的主要特征通过假设、参数、变量及它们之间的联系清晰地揭示出来,为制定防治策略及措施提供理论依据。时间序列预测模型可将各种因素,包括未知因素的综合效应,统一蕴含在时间变量中,且该方法在资料收集上的成本较低,具有较为广阔的应用前景[14, 15, 16]。神经网络模型是基于模仿大脑神经网络结构和功能而建立的一种信息处理系统,具有自组织、自学习、高度并行、可推广性及鲁棒性和抗错误能力的特点,它能根据已学会的知识和处理问题的经验对复杂问题做出合理的判断[17, 18, 19, 20]。
本研究结果支持ARIMA模型对于我国肺结核发病率的预测。ARIMA模型及GRNN模型的拟合值与实际值比较显示:ARIMA模型的拟合值充分逼近发病率的实际值,能准确地预测出发病高峰波,相对误差绝对值仅为GRNN模型的57.19%,提示ARIMA模型比GRNN模型更适合用于我国肺结核发病率的预测。
两种模型各有特点,ARIMA模型作为一种数据处理方法,主要从数据上反映疾病的发展变化趋势。欲进一步提高预测的精度、可信性和抗风险性,可尝试在制定预防控制策略和具体措施时全面收集影响肺结核的发病因素,建立带有其他解释变量的ARIMA组合模型,或者建立以影响因素为网络输入的GRNN组合模型进行预测和分析。
| [1] | 谭慭莘,田考聪.数学模型在人群疾病预测研究中的应用[J].中国医院统计,2005,12:83-85. |
| [2] | 王 燕.应用时间序列分析[M].3版. 北京:中国人民大学出版社,2012:141-160. |
| [3] | Cryer J D, Chan K S.时间序列分析及应用[M].潘红宇,王玲玲,李瑶帆,梁丽英,关 晨,闵 敏,等译. 2版. 北京:机械工业出版社,2011:40-58. |
| [4] | 易丹辉.数据分析与Eviews应用[M].北京:中国人民大学出版社,2008:141-148. |
| [5] | Svensson J, Andersson D E. What role do changes in the demographic composition play in the declining trends in alcohol consumption and the increase of non-drinkers among swedish youth? A time-series analysis of trends in non-drinking and region of origin 1971-2012[J]. Alcohol Alcohol, 2015 Jun 30. pii: agv074. [Epub ahead of print] |
| [6] | Liu D J, Li L. Application study of comprehensive forecasting model based on entropy weighting method on trend of PM2.5 concentration in guangzhou, China [J].Int J Environ Res Public Health, 2015,12: 7085-7099. |
| [7] | Li G Z, Shao F F, Zhang H, Zou C P, Li H H, Jin J. High mean water vapour pressure promotes the transmission of bacillary dysentery [J]. PLoS One, 2015,10: e0124478. |
| [8] | Stadnytska T, Braun S, Wemer J. Comparison of automated procedures for ARMA model identification [J]. Behav Res Methods, 2008, 40: 250-262. |
| [9] | 飞思科技产品研发中心.神经网络理论与MATLAB7实现[M].北京:电子工业出版社, 2005:123-125. |
| [10] | 张德丰, 周 品,许绍兴.MATLAB神经网络应用设计[M].北京:机械工业出版社,2009:158-180. |
| [11] | 张 磊,毕 靖,郭莲英.MATLAB实用教程[M].北京:人民邮电出版社,2008:26-172. |
| [12] | Zhang G, Huang S, Duan Q, Shu W, Hou Y, Zhu S, et al. Application of a hybrid model for predicting the incidence of tuberculosis in Hubei, China [J]. PLoS One, 2013, 8: e80969. |
| [13] | Li H Z, Tao W, Gao T, Li H, Lu Y H,Su Z M. Improving the accuracy of Density Functional Theory (DFT) calculation for homolysis bond dissociation energies of Y-NO bond: generalized regression neural network based on grey relational analysis and principal component analysis [J].Int J Mol Sci, 2011, 12: 2242-2261. |
| [14] | 陈友春,朱文婕.季节ARIMA模型在我国肺结核发病率预测中的应用[J].太原师范学院学报(自然科学版),2012,11:46-49. |
| [15] | Wakefield M A, Coomber K, Durkin S J, Scollo M, Bayly M, Spittal M J, et al. Time series analysis of the impact of tobacco control policies on smoking prevalence among Australian adults, 2001-2011 [J].Bull World Health Organ, 2014, 92:413-422. |
| [16] | Zhang X, Zhang T, Young A A, Li X. Applications and comparisons of four time series models in epidemiological surveillance data [J]. PLoS One, 2014, 9: e88075. |
| [17] | Hamdy K E, Yosry A A, Farag I Y. Prediction of hourly and daily diffuse fraction using neural network, as compared to linear regression models[J]. Energy, 2007, 32: 1513-1523. |
| [18] | Baker B D, Richards C E. A comparison of conventional linear regression methods and neural networks for forecasting educational spending[J]. Econom Edu Rev, 1999, 18: 405-415. |
| [19] | Guan P, Huang D S, Zhou B S. Forecasting model for the incidence of hepatitis A based on artificial neural network. World J Gastroenterol, 2004, 10:3579-3582. |
| [20] | Yan W, Xu Y, Yang X, Zhou Y. A hybrid model for short-term bacillary dysentery prediction in Yichang City, China [J]. Jpn J Infect Dis, 2010,63:264-270. |
 2016, Vol. 37
2016, Vol. 37


