线性回归分析中，研究者通常需了解每个自变量对因变量变异的贡献大小即自变量的相对重要性。当自变量间不相关或相关性较弱时，自变量的相对重要性可由一些传统的、简单的指标表示，如标准回归系数的平方、偏相关系数的平方以及半偏相关系数的平方等。但在实际问题中，自变量间不相关的数据并不常见。近年来，国际学者提出几种关于自变量的相对重要性的估计方法，如优势分析法^{[ 1,2,3,4 ]}、比例边界方差分解法^{[ 5 ]}和相对权重^{[ 6,7,8 ]}等。但大多数学者对这些方法的使用仍存在较大的分歧，原因是这些方法构建前提条件不同，有时结果也不尽相同。本研究引用Shapley在1953年提出的对策理论(game theory)法求解当自变量间存在多重共线性时自变量的相对重要性，并用实际的医学数据探讨对策理论在医学领域中的意义和作用。

1 统计方法原理 1.1 自变量的序列重要性偏R²值计算 下面给出本研究提出的自变量的序列重要性偏R²值的概念。 假设有3个自变量，记为X_i，X_j和X_k，自变量依次以ijk次序引入回归方程，分别计算其在不同自变量构成的回归模型中相应的R²，分别记为R²₁、R²₂、R²₃，则R²₁为X_i的单独贡献值，R²₂为在已经引入X_i后再引入X_j时X_i和X_j的联合贡献值，R²₃看作是3个自变量的总的贡献值。那么(R²₂-R²₁)表示自变量X_j对对应子集的序列重要性偏R²值，同理(R²₃-R²₂)表示自变量X_k对对应子集的序列重要性偏R²值。一般地，假设对因变量有影响的自变量的个数有p个，对于某一特定的进入序列，当i=1,2,…,p时，(R²_i-R²_i-1)为第i个自变量在对应序列中的序列重要性偏R²值。当自变量个数为3时，所有自变量在不同序列中的序列重要性偏R²值计算如表 1所示。表 1中，同一自变量在不同序列中的序列重要性偏R²值不同。

表 1(Table 1)

表 1 自变量的序列重要性偏R2值计算 Tab 1 Calculation of sequence importance partial R2 of each variable Enter the model order Sequence importance partial R2 of each variable Xi Xj Xk ijk R2i R2ij-R2i R2ijk-R2ij ikj R2i R2ik-R2i R2ikj-R2ik jik R2ji-R2j R2j R2jik-R2ji jki R2jki-R2jk R2j R2jk-R2j kij R2ki-R2k R2kij-R2ki R2k kji R2kji-R2kj R2kj-R2k R2k

表 1 自变量的序列重要性偏R2值计算 Tab 1 Calculation of sequence importance partial R2 of each variable

从表 1可以看出，对于p个自变量，有p！个不同的进入序列，例如，当自变量个数为3时，就有6个不同的进入序列。上表列出当自变量个数为3时所有自变量以不同的次序进入回归模型时每个自变量的序列重要性偏R²值。 1.2 自变量重要性的估计

在实际问题中，应用线性回归模型研究影响因变量的一些因素之间往往存在多重共线性，研究者也关心在自变量的排序未知情况下影响因变量的自变量中每个自变量对因变量变异的贡献大小，也就是将模型的R²如何公平、有效地分配给每个自变量。解决这一问题的方法是对某一自变量在所有引入序列中估计的序列重要性求平均，其原理是以R²作为特征函数利用对策理论求解得出。

对策理论旨在解决的问题是：在一次多人联合参与的工作中，找到一个分配函数将合作产生的总效益公平、有效地分配给联盟中的每位参与者。Shapley在1953年首先提出了具体的解法^{[ 9 ]}，因此也被称为Shapley值法。后在1960年Roberts利用若干公理对此方法给出了严格、详细的公式证明与推导，也使得这作为一个公理被研究者广泛使用。在考虑公平、有效地分配总效益时，首先应该注意的问题是在这项工作中的每个参与者的效益之和应该等于所有参与者通过合作产生的总效益。在评估每个参与者的效益时，不能只单独考虑每个参与者单独个人的效益，还应综合考虑与其他参与者的联合贡献。理论上，根据自变量相对重要性概念，在线性回归模型中求解自变量相对重要性可以看作是这一问题的同构问题，同构性解释如下：(1)参与者看作线性回归模型中影响因素或自变量；(2)联盟看作是各个影响因素或自变量的组合；(3)特征函数看作是线性回归模型的R²；(4)效益分配看作是线性模型总变异R²的分解；(5)哑参与者看作是与因变量无关的因素或自变量。根据同构性解释，下面首先分析求解自变量重要性的Shapley值必须满足的4个公理^{[ 9 ]}，然后再给出自变量相对重要性的Shapley值定理。

假设在回归模型中有p个自变量，记为X=｛X₁,X₂,…,X_p｝；设S为自变量X中任意s(s≤p)个自变量组成的一子集；R²为用于估计每个子集的效用的实值特征函数；SV为贡献分配函数，SV=(SV₁,SV₂,…,SV_p)。

公理1(对称性公理)：如果SV_i为在S中第i个因素的贡献值，当这个因素在S中记为第j个因素时，假定这时子集记为S′，那么SV_i[R²,S]=SV_j[R²,S′]。解释为，在一个特定的子集中因素的名称对贡献值的确定无影响，贡献值的确定仅对在子集中选择的自变量和特征函数敏感。

公理2(有效性公理)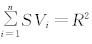：解释为，各个因素的贡献总和等于模型总变异R²，或者各个因素的贡献只能在模型的总变异R²中进行分解。

公理3(线性公理)：如果X₁和X₂是针对同一自变量集X的两个子集，有X=X₁∪X₂且X₁∩X₂=，R²₁是对X₁的任意特征值函数，R²₂是对X₂的任意特征函数，且有R²=R²₁+R²₂，则有SV[X，R²]=SV[X₁，R²₁]+SV[X₂，R²₂]。解释为，如果将自变量集X分为两个独立且完备的子集，则由该两个子集分别构成的模型的贡献和等于总模型的变异R²。

公理4(哑公理)：如果自变量X_i为在S中一个哑变量，则SV_Xi[S,R²]=0。解释为，在回归模型中，与因变量不相关性的自变量的重要性也为零。

Shapley值定理：在p个自变量X=｛X₁,X₂,…,X_p｝和以R²为特征函数的条件下，让SV=(SV₁,SV₂,…,SV_p)表示在R²上的一组值，假设每个SV_i都满足线性和哑性公理，

且SV满足对称性和有效性公理，则在SV的范围内对任意的X_i∈X都有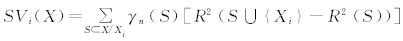，γ_n(S)= s!(p-s-1)!/p! 。 其中S为不包括自变量X_i的子集，S∪｛X_i｝为包含自变量X_i的子集，s为子集S中自变量的个数，p为所有自变量的个数。经证明R²是唯一一个满足公理1至公理4的特征函数^{[ 9 ]}。

2 实际案例分析 2.1 影响血红蛋白的因素的相关矩阵和回归分析结果

现有757例不同年龄正常人的白细胞(WBC)、红细胞(RBC)、血小板(PLT)、红细胞压积(HCT)和血红蛋白(HB)5项血常规指标，利用SAS 9.2统计分析软件，以HB为因变量，其他变量为自变量进行回归分析。因变量和自变量的相关系数矩阵见表 2。从表 2可以看出，影响HB的各个影响因素之间存在显著的相关性。首先利用逐步回归法、调整R²、C_p统计量筛选自变量，最后进入回归模型的自变量为RBC、PLT、HCT。最后估计的回归方程为：HB=－5.048 8+2.497 7RBC－0.006 5PLT+3.336 8HCT,R²=0.921 5,对方程检验F=2 940.61,P<0.000 1，说明模型具有统计学意义。

表 2(Table 2)

表 2 因变量和自变量的相关系数矩阵 Tab 2 Correlation matrix between dependent variables and independent variables WBC RBC PLT HCT HB WBC 1 - - - - RBC 0.181 4** 1 - - - PLT 0.254 9** －0.090 1* 1 - - HCT 0.198 9** 0.861 4** －0.163 0** 1 - HB 0.176 2** 0.846 1** －0.176 6** 0.958 8** 1 WBC: White blood cell; RBC: Red blood cell；PLT: Platelet；HCT : Hematocrit; HB: Hemoglobin.*: Correlation is significant at the 0.05 level (2-tailed); **: Correlation is significant at the 0.01 level (2-tailed)

表 2 因变量和自变量的相关系数矩阵 Tab 2 Correlation matrix between dependent variables and independent variables

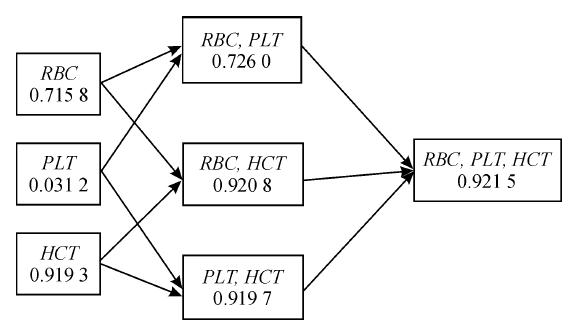
利用SAS 9.2软件，分别计算影响HB的3个自变量单独的R²、不同组合的R²以及3个自变量的总R²，计算结果如图 1所示；利用图 1计算各个自变量的序列重要性偏R²值，结果见表 3。

表 3(Table 3)

表 3 各自变量的序列重要性偏R2值 Tab 3 Sequence importance partial R2 value of RBC,PLT and HCT Enter the model order Sequence importance partial R2 value of each variable RBC PLT HCT RBC,PLT,HCT 0.715 8 0.010 2 0.195 5 RBC,HCT,PLT 0.715 8 0.000 7 0.205 0 PLT,RBC,HCT 0.694 8 0.031 2 0.195 5 PLT,HCT,RBC 0.001 8 0.031 2 0.888 5 HCT,RBC,PLT 0.001 5 0.000 7 0.919 3 HCT,PLT,RBC 0.001 8 0.000 4 0.919 3 Average value 0.355 3 0.012 4 0.553 8 RBC: Red blood cell；PLT: Platelet；HCT: Hematocrit

表 3 各自变量的序列重要性偏R2值 Tab 3 Sequence importance partial R2 value of RBC,PLT and HCT

从表 3可以看出同一个自变量以不同的次序进入回归模型时的序列重要性偏R²值不同。如本例中由3个自变量组成的6个不同序列中，同一自变量(如RBC)的边缘贡献值的变化是从0.001 5到0.715 8。从表中也可以看出对因变量影响最大的自变量是HCT，最大达到0.919 3，在测量选择上应首先考虑对HCT测量。

图 1 影响血红蛋白的自变量以不同次序进入模型的R2 Fig 1 R2 of variables entering the model in different orders

结合Shapley值定理给出的公式，利用SAS 9.2软件编写相应的程序分别计算3个自变量重要性的估计值，事实上，自变量相对重要性估计值是自变量序列重要性偏R²估计值的平均值。同时分别应用标准回归系数的平方(β²_iy)、 偏相关系数的平方(partial ρ²)、 乘积尺度(β_ir_iy)、相对权重(ε_i)、优势分析(C_i)和对策理论Shapley值(SV_i)6种方法估计每个自变量的相对重要性。结果见表 4，表中同时给出传统的自变量相对重要性测量方法结果。

表 4(Table 4)

表 4 不同方法计算的自变量相对重要性值(R2=0.921 5) Tab 4 Relative importance of variables by different methods(R2=0.921 5) Variable β2iy Partial ρ2 βiｒiy εi Ci SVi RBC 0.006 9 0.021 9 0.070 2 0.356 5 0.355 3 0.355 3 PLT 0.000 6 0.007 7 0.004 4 0.013 9 0.012 4 0.012 4 HCT Total 0.780 1 0.713 3 0.846 8 0.550 7 0.553 8 0.553 8 0.787 6 0.743 0 0.921 5 0.921 5 0.921 5 0.921 5 RBC: Red blood cell；PLT: Platelet；HCT: Hematocrit; β2iy: Suqare of standard regression coefficient；Partial ρ2: Suqare of partial correlation coefficient；βiｒiy: Product measure； εi : Relative weight；Ci : Dominance analysis；SVi: Shapley value

表 4 不同方法计算的自变量相对重要性值(R2=0.921 5) Tab 4 Relative importance of variables by different methods(R2=0.921 5)

线性回归模型应用中，自变量之间存在多重共线性时，传统的统计量确定自变量的相对重要性是不完全和失效的^{[ 10 ]},例如，本研究结果显示用标准回归系数平方和偏相关系数的平方计算的3个自变量的重要性之和分别等于0.787 6和0.743 0，都与模型总变异相差较大。其他的自变量相对重要性的估计方法所估计的自变量的重要性值总和等于模型R²。从分析结果也可以看出，优势分析和对策理论的估计结果几乎一致，原因是优势分析所用的基本思想和对策理论的基本思想一致。自变量间存在多重共线性对回归方程的预测能力并没有太大影响，但却对回归系数的估计和自变量重要性估计影响较大，从而在解释和衡量单个自变量对因变量的作用时产生较大的偏差，特别是自变量之间的共线性水平越高时，造成偏差就越大。本研究在计算序列重要性偏R²值的基础上，借助于对策理论求平均重要性的方法，这样客观、贴切地反映了各个自变量在模型中的作用大小。本研究通过利用影响HB含量的实例分析发现，在影响HB的自变量中，HCT对HB含量的影响最大，重要性估计值为0.553 8，占模型总变异的60.10%，其次是RBC，重要性估计值为0.355 3，占模型总变异的38.55%，PLT的影响不大，估计值为0.012 4，占总变异的1.34%，重要性的排序与相关性排序一致，说明分析结果是合理的。

本研究提出了序列重要性偏R²值的概念，结果显示同一自变量以不同的次序进入模型时计算的序列重要性偏R²值不同，这对一些实际的应用，如疾病的预后影响因素及在疾病预防或控制策略的选择上提供了定量的依据。另外从序列重要性偏R²值中可以找出影响因变量的自变量中，对因变量的贡献值最大的自变量(即在所有的p！个进入序列中R²_{i|1,2,…k-1,k+1,…,p}达到最大)，在构建回归模型时应首先考虑将其纳入，依次直到所有的影响因素都纳入为止，可以提高回归模型预测能力^{[ 11 ]}。

最后引用Shapley值求解自变量重要性的最重要的原因是：它不是一个探索式的理论方法而是基于4个公理推导且已经作为1个定理使用的方法^{[ 9 ]}。另外，Shapley值法为更加复杂的问题提供了一个比较接近实际的模型，原因是它比较和平均了自变量所有可能的子集构成模型的总变异R^{2[ 12 ]}。

4 利益冲突

所有作者声明本文不涉及任何利益冲突。