扩展功能
文章信息
- 林志鹏, 单敬福, 陈乐, 孙千军, 王义武, 汪菲
- LIN ZhiPeng, SHAN JingFu, CHEN Le, SUN QianJun, WANG YiWu, WANG Fei
- 基于地貌形态学交融的现代曲流河道迁移构型表征
- Geomorphology Processes of Channel Planform Migration on Modern Meandering Rivers
- 沉积学报, 2018, 36(3): 427-445
- ACTA SEDIMENTOLOGICA SINCA, 2018, 36(3): 427-445
- 10.14027/j.issn.1000-0550.2018.045
-
文章历史
- 收稿日期:2017-05-19
- 收修改稿日期: 2017-08-22
2. 长江大学地球科学学院, 武汉 430100;
3. 中国地质大学能源学院, 北京 100083;
4. 北京大学地球与空间科学学院, 北京 100871;
5. 大庆油田采气分公司, 黑龙江大庆 163000
2. School of Geosciences, Yangtze University, Wuhan 430100, China;
3. School of Energy Resources, China University of Geosciences, Beijing 100083, China;
4. School of Earth and Space Sciences, Peking University, Beijing 100871, China;
5. Gas Production Company of Daqing Oilfield Limited Company, Daqing, Heilongjiang 163000, China
推演重建曲流河道构型及其沉积演化过程需重点把握地貌形态迁移结构和演化规律,现阶段这项基础性理论研究相对不足。对现代曲流河地貌迁移规律的认知是深入解剖地下河流储层构型的钥匙,也是恢复古河道历史演化过程的一种重要科学方法[1-5],且河流相砂体内部结构十分复杂,传统方法难以精确揭示储层内部结构单元分布和预测油气的运移模式[6-10]。通过曲流河道地貌迁移规律的构型表征,有助于指导古河道砂体地下空间构型的分布特征[11-14]。结合地貌形态学的理论和方法则是其中至关重要的研究手段之一。尽管对古代和现代河流沉积体系已存大量研究,但曲流河动态地貌的过程演化分析依然是极具挑战的任务[13, 15]。国内外许多经典文章从河道的规模估算到水动力学及数值模拟等方面尝试对河流三维动态迁移结构进行深层次解析,如Leopold et al.[16]对河道水动力学特征、曲流结构、模式[17]以及河流地貌学特征[18]等做过详细研究,并取得一定的成果;Wolman et al.[19]通过对地貌过程分析认为河流周期性的流量变化是控制河流形态的重要因素,并结合实例追踪研究河流演化过程;Williams[20]通过对水流通量的研究提出满岸流量的定义和算法;Brice[21]提出曲流环的4种迁移模式,包括对称、不对称、复合对称和复合不对称模式;Hooker[22-24]对曲流河道地貌形态学做了大量研究,总结并提出了河弯变形的7种基本类型和3种复合类型;Miall[25-28]对河流体系的研究得出最好的线索还是结合野外露头的结论,从构型要素到沉积演化的不断深入重建历史过程。Willis et al.[13]通过三维模拟河道迁移模式,进一步提出曲流环的平移、旋转、扩张和复杂模式。Ielpi et al.[15], Ghinassi et al.[29]和Wu et al.[30]近年来则开始尝试通过结合地貌形态学的方法来恢复古河道特征,实现动态地貌过程演化分析。相比国外,国内则更多是关注地下储层结构,对曲流河形态的研究主要集中在侧积体的概念性划分。裘怿楠[31]对河流形态对河型的控制做了详细说明;薛培华[14]将曲流点坝沉积建造单元分为侧积面、侧积层、侧积体,结合拒马河现代沉积剖面对侧积体发育与演化过程进行解剖;尹燕义等[32]通过对现代饮马河点坝的三维解剖,对其内部侧积体沉积特征进行了详细研究;岳大力等[33]提出地下点坝识别及内部结构精细解剖的方法,并将其应用于识别古代点坝沉积;周银邦等[34]通过现代露头与构型研究分析了点坝侧积体结构形成的控制因素;单敬福等[35]结合对点坝内部侧积体“成因”的研究,探讨了曲流河道现代沉积的规律对再现古代沉积演化过程的意义;林志鹏等[3, 36]通过结合曲流河地貌动力学理论,对曲流河道迁移构型结构提出了新的量化表征思路。综合看来,对于曲流河迁移构型的研究,国外起步虽早,但总体较为分散,国内则稍显欠缺,大部分研究尚未有效结合地貌形态学理论,在没有弄清河道迁移演化规律的基础上进行的储层表征思路,需要得到纠正。
对现代曲流河道迁移结构的精细表征是解剖河流沉积过程和恢复古河道的重要方法和参考依据。曲流河道地貌迁移演化规律的不同,会影响储层单元的岩性和储集物性,河道平移、旋转、扩张等变化都会引起河道形态的改变,进而影响储层构型[23, 37-38]。近年来诸多学者着手河流地貌形态学理论,取得了显著的成果,如Ielpi et al.[15]通过对英国约克郡斯卡伯勒北部曲流河构型和动态地貌学的分析,结合现代露头的平面和剖面特征,提出了适用于该流域的一套综合河道迁移结构模型;Wu et al.[30, 39]通过对复合点坝露头地貌迁移形态的重建分析了河流沉积演化过程,并建立了一种半定量的河道迁移模式;Ghinassi et al.[29, 40]通过研究曲流河道的迁移模式,探讨了重建古河流系统和开发河流相油气藏的重要方法;吴胜和等[41]提出“层次约束、模式拟合和多维互动”的构型分析与建模思路,论述地下古河道储层结构的演化方法;单敬福等[42]通过探讨“初末流线包络线法”还原古河流迁移形态,重建河道演化过程。近年来也有大量成果通过数值模拟技术加以研究,如Asahi et al.[43]通过数值模拟计算曲流河繁复的演化过程,并探讨河道演化过程的可预测性。Schuurman[44]结合河流动力学数值模拟技术解释河流地貌演化过程;Rousseau et al.[45]通过给定曲流河初始的水流参数和地形条件,同时改变相关河流参数进行数值模拟,从而得到多种演化模型以指导和预测同等地质条件下的河道形态演化。Schuurman et al.[5]通过建立地形数值模型实验来观测曲流河点坝的形态变化和迁移状况。由此进一步证明,揭示河道过程演化离不开河流地貌形态学与沉积学科的交融。
鉴于此,本文通过Google Earth和ACME Mapper(基于Google Earth的高精度通用绘图应用程序)获取高分辨率历史卫星图像,结合两条天然曲流河道的迁移结构,采用新的精细构型表征参数法,实现河道地貌迁移构型表征,得出其迁移规律与模式。拟主要解决以下四个问题:1)提出一套完善的曲流河地貌迁移形态构型表征方案;2)结合不同曲流河道迁移特征进行历史演化过程形态学分析,并对其结构加以详细刻画;3)针对不同迁移结构,应用表征参数归纳一套完整的曲流河道迁移模型;4)探讨迁移结构对地下储层构型的重要指导意义。
1 地质背景天然河道的选择需要着重考虑人类活动因素,且不同地区不同曲流河具有的特征差异性也需要加以研究,为更好展示不同地域河流的特征,本文选取2条来自不同国家、人口分布分散、自然环境和河道结构保存较为完整、易于观察的典型曲流河作为研究对象,每条河流各选取50条河曲进行统计分析,并选取其中12段河曲进行精细表征。这2条河流分别为额尔齐斯河和诺威特纳河。
额尔齐斯河(Irtysh River)是鄂毕河(Ob River)最大的支流之一,全长约4 248 km,源起中国新疆维吾尔自治区阿尔泰山南坡,自东南向西北流出中国,经哈萨克斯坦向北流入俄罗斯,在汉特—曼西斯克汇入鄂毕河。研究河段南起托博尔斯克北部,坐标为60°56′N,69°19′E,如图 1中IR:Ⅰ-Ⅱ,河段长44.51 km,直线距离为22.99 km。该河段曲流河结构保存较好,易于观察。

|
| 图 1 额尔齐斯河与诺威特纳河研究区位置图 A.额尔齐斯河,IR:Ⅰ-Ⅱ为研究河段;B.诺威特纳河,NR:Ⅰ-Ⅱ为研究河段;坐标信息源于Google Earth和ACME Mapper Figure 1 Location map of the Irtysh River and Nowitna River |
诺威特纳河(Nowitna River)位于美国阿拉斯加州国家野生动物保护区,为育空河(Yukon River)一支流,属于典型的曲流河,自北部卡斯科奎姆山流经诺威特纳国家野生动物保护区一直流向塔纳诺西南地区汇入育空河。全长约455.45 km,流域面积达到576.27 km2,拥有众多的湖泊和沼泽,周围地形平坦,或有连绵起伏的山川丘陵,河岸植被茂盛;其中362 km被指定为野生河流,也因此现阶段很少受到人为因素的干扰,河流结构保存十分完好。研究河段北起诺威特纳河与育空河分流河口处,坐标为64°53N,205°45′E,南抵坐标为64°36′N,205°33′E的位置,如图 1中NR:Ⅰ-Ⅱ,河段长97.89 km,直线距离为35.53 km。该河段河道迁移现象显著,特征明显,有利于对原生态曲流河的迁移结构特征等进行深入研究。
2 迁移构型表征尽管现代冲积平原上大量曲流河的形态特征已被识别,但在沉积学领域对河道的刻画依然停留在沉积微相的解释中[46-48],结合地貌形态学加以精细表征的体现较少,故此结合地貌形态学与河流沉积学理论,系统完善曲流河道平面结构的构型表征。综合前人的分析[11, 13, 21, 49],将曲流河道迁移构型要素具体分为静态要素、动态要素和表征参数三大类。
2.1 静态要素静态要素指对曲流河形态结构进行定性描述的地貌沉积单元和抽象概念流线,主要包括河道内要素:河道、深洼、浅滩、深泓线、中心线、曲流环转折端和曲率顶点;河道外要素:曲流带、点坝(上游坝、中游坝、下游坝)、串沟河道、外岸(凹岸)、内岸(凸岸)、曲流环(河弯)、废弃河道、河漫滩、曲率圆和曲流环顶点等。其中对迁移结构起到重要表征作用的主要是曲流环(河弯)、中心线、曲流环转折端、曲率顶点、曲率圆、点坝(上游坝、中游坝、下游坝)和深泓线。
曲流环(Meander loop),又称河弯,是河道蜿蜒过程中的某段环状弯曲,如图 2中(4)和(5)所限定的范围就是一个单一曲流环,是曲流河道的基本构成单元。一条曲流河本质上总是可以分为数段连续的曲流环。中心线(Centerline)是河道所有横截面外岸与内岸边缘中点的连线,是抽象概念线条,其长度表示为LC(图 2);线上每点都能代表河道某个横截面的平面几何中心,在对河道进行线性研究和形态学研究时,可近似将中心线作为河道本身,此概念的使用使得对河道流线的研究和迁移轨迹有了更加便捷和明确的表示,不用考虑外岸与内岸距离的差异。曲流环转折端(Bend inflection)是两相邻曲流环的过渡位置,形态学上即是曲流带轴向线与中心线的交点(图 2);转折端的出现表明河道的迁移方向发生改变,是识别不同曲流环的重要标志。曲率顶点(Curvature apex)是曲流环外岸顶点与内岸顶点连线的中点,也是曲流环轴向线与中心线的交点(图 2);其迁移方向也可指示曲流环的迁移方向。曲率圆(Curvature circle)是表示单一曲流环弯曲程度的几何圆(图 2),为相邻两个曲流环转折端连线的中点,以连接该中点和曲率顶点之间的线段作为直径所的圆就是曲率圆,其圆心一般落在点坝中游坝附近,圆周越大,表示曲流环弯曲程度越大;圆周越小,表示曲流环弯曲程度越小。点坝(Point bar)又称心滩,是河道迁移摆动和沉积物堆积的重要沉积单元,发育于河道内岸,是曲流环的主体(图 2),据其形态位置又可定性分为上游坝(Upstream bar)、中游坝(Central bar)和下游坝(Downstream bar),其水流强度和沉积物颗粒大小与种类各有差异。深泓线(Thalweg),也称最深谷底线,是河道内海拔最低点的连线(图 2);是抽象概念线条,所代表的流域流速相对较高,谷底遭受冲蚀程度最大,总是偏向外岸一侧。
动态要素指从静态要素中提取出来的动态参数,是河道结构的量化反映,其数值变化一定程度上可指示河道演化过程。包括标量要素:曲流带宽、曲流带长、单一曲流带宽、单一曲流带长、单一曲流环宽、单一曲流环长、中心线长和曲率半径;矢量要素:曲流带轴向、曲流环轴向、上游偏转角和下游偏转角(表 1、图 2)。
| 河流河曲编号 | 额尔齐斯河 | 诺威特纳河 | |||||||||||
| 1 | 2 | 11 | 18 | 31 | 38 | 18 | 29 | 30 | 36 | 41 | 50 | ||
| 纬度 | 58°52′N | 58°56′ N | 59°20′ N | 59°34′ N | 60°14′ N | 60°40′ N | 64°45′N | 64°41′N | 64°42′N | 64°40′N | 64°39′N | 64°35′N | |
| 经度 | 68°47′E | 68°50′E | 68°52′E | 69°17′E | 69°48′E | 69°52′E | 205°40′E | 205°34′E | 205°32′E | 205°27′E | 205°30′E | 205°39′E | |
| WM/m | 16 520.9 | 14 479.6 | 13 068.9 | 14 855.1 | 10 522.0 | 22 592.7 | 9 299.9 | 10 283.3 | 10 327.0 | 12014.7 | 10 044.3 | 8770.7 | |
| LM /m | 302 741 | 302 741 | 302 741 | 302 741 | 302 741 | 302 741 | 55 458.0 | 55 458.0 | 55 458.0 | 55 458.0 | 55 458.0 | 55 458.0 | |
| WSM/m | 12 263.0 | 9 765.0 | 2 467.3 | 12 230.8 | 7 394.3 | 13 075.5 | 1 774.7 | 4 111.8 | 3 941.5 | 1 873.8 | 3 201.4 | 2 217.4 | |
| LSM/m | 11 094.8 | 11 813.2 | 8 409.4 | 23 525.6 | 17 068.8 | 18 441.5 | 3 660.9 | 6 970.9 | 7 339.3 | 6 217.5 | 7 918.2 | 3 336.5 | |
| WML/m | 3 821.3 | 2 541.6 | 1 758.1 | 3 225.5 | 2 642.6 | 3 309.8 | 654.8 | 1 022.0 | 2 269.6 | 700.2 | 715.9 | 592.0 | |
| LML/m | 919.7 | 2 472.9 | 3 551.9 | 7 637.9 | 2 282.7 | 3 145.0 | 727.9 | 1 078.1 | 1 186.1 | 684.8 | 1 221.3 | 425.6 | |
| LC/m | 10 166.9 | 7 305.9 | 4 626.3 | 11 994.3 | 6 999.2 | 6 315.5 | 1 608.9 | 2 487.3 | 4 578.9 | 1 884.5 | 2 300.0 | 1 547.8 | |
| R/m | 2 155.3 | 1 389.6 | 729.7 | 2148.5 | 1318.1 | 1 311.9 | 300.1 | 465.8 | 866.5 | 355.3 | 456.6 | 296.9 | |
| |AXMB|/m | 919.7 | 2 472.8 | 3 551.9 | 7 637.9 | 2 282.7 | 3 145.0 | 727.9 | 1 078.1 | 1 186.1 | 684.8 | 1 221.3 | 425.6 | |
| AXMB/° | 344.3 | 103.7 | 211.8 | 226.9 | 49.7 | 336.5 | 237.2 | 292.3 | 278.6 | 279.8 | 109.8 | 130.9 | |
| AXML/° | 44.0 | 136.9 | 311.9 | 94.4 | 316.8 | 110.1 | 143.7 | 174.2 | 311.2 | 16.8 | 58.5 | 29.3 | |
| θU/° | 9 | 20 | 50 | 18 | 30 | 34 | 32 | 21 | 23 | 26 | 43 | 18 | |
| θD/° | 12 | 13 | 55 | 55 | 28 | 15 | 34 | 46 | 11 | 30 | 22 | 22 | |
| S | 11.05 | 2.95 | 1.30 | 1.57 | 3.07 | 2.01 | 2.21 | 2.31 | 3.86 | 2.75 | 1.88 | 3.64 | |
| C | 0.000 5 | 0.000 7 | 0.001 4 | 0.000 5 | 0.000 8 | 0.000 8 | 0.003 3 | 0.002 1 | 0.001 2 | 0.002 8 | 0.002 2 | 0.003 4 | |
| Δθ/° | -3 | 7 | -5 | -37 | 2 | 19 | -2 | -25 | 12 | -4 | 21 | -4 | |
| Δθ′/° | 3 | -7 | 5 | 37 | -2 | -19 | 2 | 25 | -12 | 4 | -21 | 4 | |
| KM | 0.22 | 0.89 | 2.43 | 1.78 | 0.87 | 1.20 | 1.21 | 1.16 | 0.68 | 0.96 | 1.34 | 0.72 | |
曲流带宽(WM)指完整多期复合河道的迁移摆动宽度,如图 2中(1)宽度所示,包含整个复合河道最宽距离;其值随河流规模不同而不同,范围从几百米到上万米,本研究区WM为8 700~22 000 m。曲流带长(LM)指完整多期复合河道的跨域长度,即一条河流从开始到结束曲流带轴向线的长度,图 3中只能表示所研究的某单一曲流带长,所以没有标注LM;用轴向线代替直线长度融入了河道地貌形态的考虑,其变化范围区间很大,可从数千米到上万米,本研究区两条河流LM分别为302 741 m和55 458 m。单一曲流带宽(W SM)指单一河道的迁移摆动宽度,如图 2中(2)宽度所示,一般大于两倍单一曲流环宽度,其值一般为数百米到上万米,本研究区W SM为1 800~12 000 m。单一曲流带长(LSM)指单一河道的跨域长度,即单一河道轴向线的长度,如图 2中(3)长度所示。其值变化灵活,根据所研究对象规模不同而改变,本研究区LSM为3 300~23 000 m。单一曲流环宽(WML)指曲流环顶点到曲流带轴向的垂直距离,如图 2中(4)宽度所示。其值一般为数百米到上千米,本研究区WML为700~3 800 m。单一曲流环长(LML)指相邻两曲流环转折端之间的直线距离,如图 2中(5)长度所示。其值一般为数十米到上千米,本研究区LML为400~7 600 m。中心线长(LC)即是河道中心线的长度,其值可反映研究河段的实际长度,根据河流规模其值变化范围较大,本研究区LC为1 600~11 000 m。曲率半径(R)即曲率圆的半径,其值为曲率顶点到相邻曲流环转折端中点距离的一半,如图 3中(6)长度所示。其值一般为数十米到上百米,本研究区R为300~2 000 m。曲流带轴向(AXMB)指曲流带蜿蜒摆动的中心轴,是各曲流环转折端的连线,其方向指向河流流动方向,当研究某单一曲流环时,其长度近似等于LML长度。本研究区AXMB长度为400~7 600 m,方向为50°~340°。曲流环轴向(AXML)指曲流环流动的中心轴,是曲流环顶点与对应两转折端中点的连线,其方向指向外岸扩张方向,本研究区AXML方向为44°~310°。上游偏转角(θU)指曲率顶点和对应上游曲流转折端连线与曲流环轴向的夹角,如图 2中(9)角度所示;下游偏转角(θD)指曲率顶点和对应下游曲流转折端连线与曲流环轴向的夹角,如图 2中(10)角度所示,根据曲流环形态的不同,夹角范围介于0°~90°之间,且上游偏转角和下游偏转角的差值是判断迁移结构的重要依据。本研究区θU为9°~50°,θD为12°~55°。

|
| 图 3 对称扩张结构迁移构型表征 IR1为额尔齐斯河研究区内河曲11近30年来通过Google Earth拍摄的卫星图像,坐标为59°20′N,68°52′E,选取4张,其中①摄于1984年12月,②摄于1994年12月,③摄于2004年12月,④摄于2014年12月;IR2为对IR1中河曲11迁移结构要素的平面刻画;IR3为河曲11的迁移结构表征参数统计数据。NR1为诺威特纳河研究区内河曲18近2年来通过Google Earth拍摄的卫星图像,坐标为64°45′N,205°40′E,选取2张,其中①摄于2011年3月,②摄于2012年6月;NR2为对NR1中河曲18迁移结构要素的平面刻画;NR3为河曲18的迁移结构表征参数统计数据 Figure 3 Planform migration architecture of the symmetrical expansion structure |
静态要素和动态要素可刻画河道形态结构,但地貌迁移特征的量化表征与规律性模式,还需要对结构参数做特征分析,得到河道结构动态演化的变量,即表征参数。依据结构要素,提炼出5个曲流河道迁移构型表征参数:弯度指数、曲率、顺流偏转角差、逆流偏转角差和扩张系数,其中顺流偏转角差、逆流偏转角差和扩张系数为本文首次提出的表征参数;同时弯度指数与曲率的定义也更为精确。
弯度指数(S)是指研究河道范围内,中心线长度与曲流带轴向线长的比值。前人对弯度指数的定义是河道长度与河谷长度的比值,但这一定义存在的问题是,河道与河谷长度区分不清晰,是外岸线、内岸线、深泓线、中心线长度,还是河道起点和终点的直线段长度,容易引起混淆。采用中心线长度代表河道长度可统一内、外岸线的问题,曲流带轴向线长度代表河谷长度,其一不会引起概念模糊;其二,轴向线长度比河道起点和终点的直线段长度能更真实地反映地貌迁移情况,因为它考虑了河道随地形蜿蜒变化的因素,而非单一简化地当做一条直线处理。用公式表示为:
 (1)
(1)
曲率(C)指曲率半径的倒数,表示河弯的弯曲程度,曲率越小,表示河弯程度越大;反之则越小。已有通过点坝弧长直接除点坝直径计算曲率的方法[50],因为点坝形态不规则,提取的直径和弧长很不明确,误差较大。选择曲率半径,通过转折端来确定河曲开始迁移的起点,再结合曲率顶点,控制整个曲流环形态,最终以曲率顶点和对应两转折端3点确定的曲率圆则能更有效反映曲率的真实情况。用公式表示为:
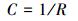 (2)
(2)
顺流偏转角差(Δθ)指上游偏转角与下游偏转角的差值,用以反映河弯对称性。差值越接近于0,表明曲流环对称性越高,差值为正且越大,表明曲率顶点更靠近上游转折端,呈逆流旋转趋势;差值为负且越小,表明曲率顶点更靠近下游转折端,呈顺流旋转趋势。用公式表示为:
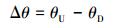 (3)
(3)
逆流偏转角差(Δθ′),与顺流偏转角差对应相反,指下游偏转角与上游偏转角的差值,差值越接近于0,表明曲流环对称性越高,差值为正且越大,表明曲率顶点更靠近下游转折端,呈顺流旋转趋势;差值为负且越小,表明曲率顶点更靠近上游转折端,呈逆流旋转趋势。用公式表示为:
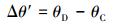 (4)
(4)
扩张系数(KM)指单一曲流环长与曲率直径(2R)的比值,因为它们都由转折端和曲率顶点控制,所以基本能控制曲流环形态,曲流环若不断往外扩张,受转折端控制,曲率直径会逐渐变大,而曲流环长则改变幅度较小;当曲流环扩大到一定程度开始收敛,走向截弯趋势时,受转折端控制,曲率直径一般会大于曲流环长。因此,他们可以对河道的扩张收敛情况提供基本的量化反映。比值大于1,则说明处于扩张期,比值越大,扩张程度越小;比值小于1,则说明处于收敛期,比值越小,收敛程度越大。用公式表示为:
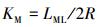 (5)
(5)
研究河段的基本结构表征要素和参数数据可见表 1。
3 地貌形态迁移构型特征对点坝侧积形态和河道演化的定性描述缺乏量化表征,本文结合形态结构表征参数,对研究区曲流河道迁移演化规律进行定量研究。因为河流对堤岸的作用总是侵蚀凹岸,堆积凸岸,当点坝侧向堆积至一定程度时易发生截弯取直,随之重复新一轮侧积侵蚀过程,所以曲流河道整体迁移构型宏观上总呈现出重复性不断向外扩展的趋势。具体根据迁移前后河道地貌形态演化特征,并结合表征参数的定量刻画,可将曲流河道迁移构型具体分为扩张结构和收敛结构两大类。
3.1 扩张结构曲流河扩张结构(Expansion Structure,ES)指河道向外不断侧积侵蚀迁移,KM通常大于1。根据曲流环和点坝向上游和下游摆动的幅度与Δθ值的差异,可细分为对称扩张结构、上游旋转(逆流旋转)扩张结构和下游旋转(顺流旋转)扩张结构。
3.1.1 对称扩张结构曲流环不断向外岸侧积侵蚀,对称性好,KM大于1,Δθ靠近0°,此为曲流河对称扩张结构(Symmetrical Expansion Structure,SES)。如图 3中IR1表明从1984年到2014年,额尔齐斯河研究区内河曲11迁移不明显,通过IR2迁移结构表征和IR3表征参数的计算分析,可见该曲流环S为1.3,C为0.001 4,反映弯曲程度较低;Δθ为-5°,表明曲流环对称性较好,呈弱顺流旋转趋势;KM为2.43,表明河弯处于扩张期,且扩张程度较小。综合表明河曲11为SES。NR1中诺威特纳河2011年到2012年的卫星图像显示河曲18几乎没有发生迁移,通过NR2迁移结构表征和NR3表征参数的计算分析,可见该曲流环S为2.21,C为0.003 3,反映弯曲程度较大;Δθ为-2°,表明曲流环对称性较好,呈弱顺流旋转趋势;KM为1.21,表明河弯处于扩张期,且扩张程度较大。综合表明河曲18为SES。
3.1.2 上游旋转(逆流旋转)扩张结构曲流环不断向外岸侧积侵蚀,且曲率顶点更靠近上游转折端,呈逆流旋转趋势,KM大于1,Δθ大于0°,此为曲流河上游旋转(逆流旋转)扩张结构(Upstream Rotation Expansion Structure,URES)。如图 4中IR4表明从1984年到2014年,额尔齐斯河研究区内河曲38迁移不明显,通过IR5迁移结构表征和IR6表征参数的计算分析,可见该曲流环S为2.01,C为0.000 8,反映弯曲程度较大;Δθ为19°,表明曲率顶点更靠近上游转折端,呈逆流旋转趋势;KM为1.20,表明河弯处于扩张期,且扩张程度较大。综合表明河曲38为URES。NR4中诺威特纳河2011年到2013年的卫星图像显示河曲41迁移不明显,通过NR5迁移结构表征和NR6表征参数的计算分析,可见该曲流环S为1.88,C为0.002 8,反映弯曲程度较大;Δθ为21°,表明曲率顶点更靠近上游转折端,呈逆流旋转趋势;KM为1.34,表明河弯处于扩张期,且扩张程度较大。综合表明河曲41为URES。

|
| 图 4 上游旋转(逆流旋转)扩张结构迁移构型表征 IR4为额尔齐斯河研究区内河曲38近30年来通过Google Earth拍摄的卫星图像,坐标为60°40′N,69°52′E,选取4张,其中①摄于1984年12月,②摄于1994年12月,③摄于2004年12月,④摄于2014年12月;IR5为对IR4中河曲38迁移结构要素的平面刻画;IR6为河曲38的迁移结构表征参数统计数据。NR4为诺威特纳河研究区内河曲41近2年来通过Google Earth拍摄的卫星图像,坐标为64°39′N,205°30′E,选取2张,其中①摄于2011年3月,②摄于2013年3月;NR5为对NR4中河曲41迁移结构要素的平面刻画;NR6为河曲41的迁移结构表征参数统计数据 Figure 4 Planform migration architecture of the upstream rotation expansion structure |
曲流环不断向外岸侧积侵蚀,且曲率顶点更靠近下游转折端,呈顺流旋转趋势,KM大于1,Δθ小于0°,此为曲流河下游旋转(顺流旋转)扩张结构(Downstream Rotation Expansion Structure,DRES)。如图 5中IR7表明从1984年到2013年,额尔齐斯河研究区内河曲18迁移缓慢,通过IR8迁移结构表征和IR9表征参数的计算分析,可见该曲流环S为1.57,C为0.000 5,反映弯曲程度较大;Δθ为-37°,表明曲率顶点更靠近下游转折端,呈顺流旋转趋势;KM为1.78,表明河弯处于扩张期,且扩张程度较大。综合表明河曲18为DRES。NR7中诺威特纳河2011年到2012年的卫星图像显示河曲29河道迁移缓慢,通过NR8迁移结构表征和NR9表征参数的计算分析,可见该曲流环S为2.31,C为0.002 1,反映弯曲程度较大;Δθ为-25°,表明曲率顶点更靠近下游转折端,呈顺流旋转趋势;KM为1.16,表明河弯处于扩张期,且扩张程度较大。综合表明河曲29为DRES。

|
| 图 5 下游旋转(顺流旋转)扩张结构迁移构型表征 IR7为额尔齐斯河研究区内河曲18近30年来通过Google Earth拍摄的卫星图像,坐标为64°45′N,154°20′E,选取4张,其中①摄于1984年12月,②摄于1994年12月,③摄于2004年12月,④摄于2013年12月;IR8为对IR7中河曲18迁移结构要素的平面刻画;IR9为河曲18的迁移结构表征参数统计数据。NR7为诺威特纳河研究区内河曲29近2年来通过Google Earth拍摄的卫星图像,坐标为64°41′N,205°34′E,选取2张,其中①摄于2011年3月,②摄于2012年3月;NR8为对NR7中河曲29迁移结构要素的平面刻画;NR9为河曲29的迁移结构表征参数统计数据 Figure 5 Planform migration architecture of the downstream rotation expansion structure |
曲流河收敛结构(Constriction Structure,CS)指河道在向外扩张过程到达一定阶段,开始发生向曲流带轴向截弯侵蚀的过程,表现为河道扩张趋势明显减缓,并在转折端附近侵蚀程度加深,最终截弯废弃。这种结构截弯KM通常小于1。根据曲流环和点坝向上游和下游摆动幅度与Δθ值的差异,可细分为对称收敛结构、上游旋转(逆流旋转)收敛结构和下游旋转(顺流旋转)收敛结构。
3.2.1 对称收敛结构曲流环向外扩张过程减缓,在转折端附近开始侵蚀截弯,KM小于1,Δθ靠近0°且形态对称,此为曲流河对称收敛结构(Symmetrical Constriction Structure,SCS)。如图 6中IR10表明从1984年到2015年,额尔齐斯河研究区内河曲31河道迁移较缓,通过IR11迁移结构表征和IR12表征参数的计算分析,可见该曲流环S为3.07,C为0.000 8,反映弯曲程度较大;Δθ为2°,形态近似对称,表明曲流环对称性较好,呈微弱逆流旋转趋势;KM为0.87,表明河弯处于收敛期,且收敛程度较小。综合表明河曲31为SCS。NR10中诺威特纳河2011年到2013年的卫星图像显示河曲36河道迁移不显著,通过NR11迁移结构表征和NR12表征参数的计算分析,可见该曲流环S为2.75,C为0.002 8,反映弯曲程度较大;Δθ为-4°,形态近似对称,表明曲流环对称性较好,呈微弱顺流旋转趋势;KM为0.96,表明河弯处于收敛期,且收敛程度较小。综合表明河曲36为SCS。

|
| 图 6 对称收敛结构迁移构型表征 IR10为额尔齐斯河研究区内河曲31近30年来通过Google Earth拍摄的卫星图像,坐标为60°14′N,69°48′E,选取4张,其中①摄于1984年12月,②摄于1994年12月,③摄于2004年12月,④摄于2015年7月;IR11为对IR10中河曲31迁移结构要素的平面刻画;IR12为河曲31的迁移结构表征参数统计数据。NR10为诺威特纳河研究区内河曲36近2年来通过Google Earth拍摄的卫星图像,坐标为64°40′N,205°27′E,选取2张,其中①摄于2011年12月,②摄于2013年3月;NR11为对NR10中河曲36迁移结构要素的平面刻画;NR12为河曲36的迁移结构表征参数统计数据 Figure 6 Planform migration architecture of the symmetrical constriction structure |
曲流环向外扩张过程减缓,在转折端附近开始侵蚀截弯,且曲率顶点更靠近上游转折端,呈逆流旋转趋势,KM小于1,Δθ大于0°,此为曲流河上游旋转(逆流旋转)收敛结构(Upstream Rotation Constriction Structure,URCS)。如图 7中IR13表明从1984年到2016年,额尔齐斯河研究区内河曲2河道迁移较缓,通过IR14迁移结构表征和IR15表征参数的计算分析,可见该曲流环S为2.95,C为0.000 7,反映弯曲程度较大;Δθ为7°,曲率顶点更靠近上游转折端,呈逆流旋转趋势;KM为0.89,表明河弯处于收敛期,且收敛程度较大。综合表明河曲2为URCS。NR13中诺威特纳河2011年到2013年的卫星图像显示河曲30河道迁移不明显,通过NR14迁移结构表征和NR15表征参数的计算分析,可见该曲流环S为3.86,C为0.001 2,反映弯曲程度较大;Δθ为12°,曲率顶点更靠近上游转折端,呈逆流旋转趋势;KM为0.68,表明河弯处于收敛期,且收敛程度较大。综合表明河曲30为URCS。
3.2.3 下游旋转(顺流旋转)收敛结构曲流环向外扩张过程减缓,在转折端附近开始侵蚀截弯,且曲率顶点更靠近下游转折端,呈顺流旋转趋势,KM大于1,Δθ小于0°,此为曲流河下游旋转(顺流旋转)收敛结构(Downstream Rotation Constriction Structure,DRCS)。如图 8中IR16表明从1984年到2016年,额尔齐斯河研究区内河曲1河道迁移过程较缓,通过IR17迁移结构表征和IR18表征参数的计算分析,可见该曲流环S为11.05,C为0.000 5,反映弯曲程度很大;Δθ为-3°,曲率顶点更靠近下游转折端,呈顺流旋转趋势;KM为0.22,表明河弯处于收敛期,且收敛程度较大。综合表明河曲1为DRCS。NR16中诺威特纳河2010年到2013年的卫星图像显示河曲50河道迁移较缓,通过NR17迁移结构表征和NR18表征参数的计算分析,可见该曲流环S为3.64,C为0.003 4,反映弯曲程度较大;Δθ为-4°,曲率顶点更靠近下游转折端,呈顺流旋转趋势;KM为0.72,表明河弯处于收敛期,且收敛程度较大。综合表明河曲50为DRCS。

|
| 图 7 上游旋转(逆流旋转)收敛结构迁移构型表征 IR13为额尔齐斯河研究区内河曲2近30年来通过Google Earth拍摄的卫星图像,坐标为58°56′N,68°50′E,选取4张,其中①摄于1984年12月,②摄于1994年12月,③摄于2005年8月,④摄于2016年8月;IR14为对IR13中河曲2迁移结构要素的平面刻画;IR15为河曲2的迁移结构表征参数统计数据。NR13为诺威特纳河研究区内河曲30近2年来通过Google Earth拍摄的卫星图像,坐标为64°42′N,205°32′E,选取2张,其中①摄于2011年12月,②摄于2013年3月;NR14为对NR13中河曲30迁移结构要素的平面刻画;NR15为河曲30的迁移结构表征参数统计数据 Figure 7 Planform migration architecture of the upstream rotation constriction structure |
通过对迁移构型表征的刻画与分析,可以对曲流河道迁移模式的普适性规律进行探讨。由于河道中心线可近似代替主河道,故本文采用中心线代表河道结构以简化表示曲流河迁移过程和建立迁移构型模式的目的;结合上述构型表征的特征,建立如下曲流河道理想化条件下迁移构型模式的6种常规模式和3种基本复合模式(图 9)。

|
| 图 9 理想条件下曲流河道地貌迁移模式 SEM为对称扩张迁移模式,UREM为上游旋转扩张迁移模式,DREM为下游旋转扩张迁移模式,SCM为对称收敛迁移模式,URCM为上游旋转收敛迁移模式,DRCM为下游旋转收敛迁移模式,SE-CM为对称扩张—收敛迁移模式,URE-CM为上游旋转扩张—收敛迁移模式,DRE-CM下游旋转扩张—收敛迁移模式。A为河道迁移过程简化示意图,B为迁移结构表征参数值随河道迁移的变化趋势示意图 Figure 9 Planform migration model of the meandering channel under the ideal condition |
曲流河道不断侧向迁移,曲率顶点近似呈直线迁移,LC逐渐增大,|AXMB|保持相对稳定,缓慢减小,S逐渐增大;R逐渐增加,C逐渐减小;θU和θD基本保持稳定不变,Δθ和Δθ′基本维持在0°左右;LML保持相对稳定,缓慢减小,KM始终大于1;如图 9中SEM,此为曲流河对称扩张迁移模式(Symmetrical Expansion Migration,SEM),见图 3中IR1和NR1。
4.1.2 上游旋转(逆流旋转)扩张迁移模式曲流河道不断侧向迁移,曲率顶点向上游方向呈曲线迁移,LC逐渐增大,|AXMB|保持相对稳定,缓慢减小,S逐渐增大;R逐渐增加,C逐渐减小;θU逐渐增大,θD逐渐减小,Δθ大于0°且逐渐增大,Δθ′小于0°且逐渐减小;LML保持相对稳定,缓慢减小,KM始终大于1;如图 9中UREM,为曲流河上游旋转(逆流旋转)扩张迁移模式(Upstream Rotation Expansion Migration,UREM),见图 4中IR4和NR4。
4.1.3 下游旋转(顺流旋转)扩张迁移模式曲流河道不断侧向迁移,曲率顶点向下游方向呈曲线迁移,LC逐渐增大,|AXMB|保持相对稳定,缓慢减小,S逐渐增大;R逐渐增加,C逐渐减小;θU逐渐减小,θD逐渐增大,Δθ小于0°且逐渐减小,Δθ′大于0°且逐渐增大;LML保持相对稳定,缓慢减小,KM始终大于1;如图 9 DREM,此为曲流河下游旋转(顺流旋转)扩张迁移模式(Downstream Rotation Expansion Migration,DREM),见图 5中IR7和NR7。
4.2 收敛迁移模式 4.2.1 对称收敛迁移模式曲流河道向外扩张过程减缓,在转折端附近开始侵蚀截弯,曲率顶点近似呈直线迁移,LC逐渐增大,|AXMB|逐渐减小,S逐渐增大;R逐渐增加,C逐渐减小;θU和θD基本保持稳定不变,Δθ和Δθ′基本维持在0°左右;LML逐渐减小,KM始终小于1;如图 9中SCM,此为曲流河对称收敛迁移模式(Symmetrical Constriction Migration,SCM),见图 6中IR10和NR10。
4.2.2 上游旋转(逆流旋转)收敛迁移模式曲流河道向外扩张过程减缓,在转折端附近开始侵蚀截弯,曲率顶点向上游方向呈曲线迁移,LC逐渐增大,|AXMΒ|逐渐减小,S逐渐增大;R逐渐增加,C逐渐减小;θU先增大后减小,θD先减小后增大再减小,Δθ大于且靠近0°,Δθ′小于且靠近0°;LML逐渐减小,KM始终小于1;如图 9中URCM,此为曲流河上游旋转(逆流旋转)收敛迁移模式(Upstream Rotation Constriction Migration,URCM),见图 7中IR13和NR13。
4.2.3 下游旋转(顺流旋转)收敛迁移模式曲流河道向外扩张过程减缓,在转折端附近开始侵蚀截弯,曲率顶点向下游方向呈曲线迁移,LC逐渐增大,|AXMΒ|逐渐减小,S逐渐增大;R逐渐增加,C逐渐减小;θU先减小后增大再减小,θD先增大后减小,Δθ小于且靠近0°,Δθ′大于且靠近0°;LML逐渐减小,KM始终小于1;如图 9 DRCM,此为曲流河下游旋转(顺流旋转)收敛迁移模式(Downstream Rotation Constriction Migration,DRCM),见图 8中IR16和NR16。

|
| 图 8 下游旋转(顺流旋转)收敛结构迁移构型表征 IR16为额尔齐斯河研究区内河曲1近30年来通过Google Earth拍摄的卫星图像,坐标为58°52′N,68°47′E,选取4张,其中①摄于1984年12月,②摄于1994年12月,③摄于2005年8月,④摄于2016年8月;IR17为对IR16中河曲1迁移结构要素的平面刻画;IR18为河曲1的迁移结构表征参数统计数据。NR16为诺威特纳河研究区内河曲50近2年来通过Google Earth拍摄的卫星图像,坐标为64°35′N,205°39′E,选取2张,其中①摄于2000年12月,②摄于2013年3月;NR17为对NR16中河曲50迁移结构要素的平面刻画;NR18为河曲50的迁移结构表征参数统计数据 Figure 8 Planform migration architecture of the downstream rotation constriction structure |
河道的迁移演化伴随着地貌、水动力、沉积环境等改变而不断变化,在实际迁移过程中更多是上述6种模式的复合,其中基本的复合模式主要可分为对称扩张—收敛迁移模式(Symmetrical Expansion-Constriction Migration, SE-CM)、上游旋转扩张—收敛迁移模式(Upstream Rotation Expansion-Constriction Migration,URE-CM)、下游旋转扩张—收敛迁移模式(Downstream Rotation Expansion-Constriction Migration,DRE-CM)。理论上其他更为复杂的迁移构型都可厘定为这些模式。
5 讨论以地貌形态学基础,揭示地质要素历史演化规律,进而指导认识古代沉积的过程演绎法正成为国内外地球科学研究发展的新趋势,并逐渐渗透到各地质学科。本文研究旨在融入地貌形态学的理论,深入分析和探讨曲流河道迁移演化规律,针对结构要素提出一种新的具体可行的表征参数来定量表征曲流河道迁移构型。这种基于地貌形态学与河流沉积学交融的迁移构型表征法对现代和古代河流沉积的预测与重建意义最主要体现在两方面:
5.1 现代河流迁移构型表征与预测河道的迁移演化过程受多因素控制,包括流量、堤岸抗蚀性强度、水流强度、坡度和气候等,在此多变量影响下,河流宏观迁移规律在陆相环境中的呈现方式就尤为重要;什么环境下发育哪种迁移模式,什么因素决定了某种迁移过程,迁移结构对沉积环境具有什么指示作用?而且这种因素对于曲流河和辫状河是具有普适性的,是否能对曲辫转换和共存研究提供新思路?从曲流河迁移构型衍生运用到整个河流沉积迁移体系中去。
以上这些思考都有助于深入解剖现代沉积过程。进一步考虑不同沉积体系下河道迁移构型模式的差异(图 10),这种差异性能否反馈沉积环境的特殊性?在整个分流体系(DFS)中[51-52],近物源区河道迁移改道十分迅速,且受阻于局限环境,是否迁移结构较为单一,以SE-CM为主;平原区河岸抗侵蚀性相对较差,是否迁移结构多样化,以URE-CM和DRE-CM复合为主;入海口地区,受控于三角洲河流与潮汐相互作用,迁移结构是否具有特殊性;深海河流体系中,如墨西哥海底的水下河流(图 10G),受海底地貌和洋流作用,河道演化是否遵循陆相河流迁移构型模式,亟待深究。

|
| 图 10 不同沉积体系下河流迁移构型模式分布图 河流露头照片源于现代4K超高清分辨率图像截取,A、B摄于冰岛,C摄于美国黄石国家公园,D摄于阿根廷巴塔哥尼亚高原,E摄于智利孔吉利奥国家公园,F摄于美国密西西比河三角洲,G摄于墨西哥尤卡坦半岛 Figure 10 Distribution patterns of river migration under different depositional systems |
地下古河道储层构型研究虽已蔚然成风,但正如前文所言,由于对地貌迁移规律认知不清,在进行河道内部砂体解剖时,容易采用错误的理论模型,形而上学。此处仅以一例加以说明,如图 11中,A为2013年发表的地下点坝内部结构解剖与河道演化特征分析成果,可参见原文献图 7[53]。图A为原文整篇文章的成果图,然而,通过对其河流历史演化的过程还原,如图B;可明显看出矛盾所在,第0期河道期次对应缺失,在第1期河道到第11期河道的演化过程中,河流结构明显与天然河流的演化结构相违背,自然条件下,河流不可能出现像第1期河道这样的迁移结构。由此可见,此处对点坝构型表征的结果整个不符合自然规律,而这还是在基于该区较密的井网条件下得出的结果。无疑将引起质疑,是否整套研究方法与思路都存在问题?如果结合本文的研究思路与方法,结合地貌形态学理论,考虑河道的迁移构型模式,理论上应该得出图C和D结果,如果文章还对古流向或者表征参数有测量,那么还可以对古河道的演化进行量化表征与精确重建。这也同时反映了基于地貌形态学交融的曲流河道迁移构型表征方法对河流储层构型的重要指导、重建与预测意义。

|
| 图 11 基于曲流河道地貌迁移构型模式的储层表征 Figure 11 Reservoir characterization based on the pattern of meandering channel migration |
基础理论架构的不足很可能导致方法甚至最终结果的错误,并进一步误导深入研究,2017年最新发表的成果中还依然存在该案列呈现的问题,所以本文的研究十分必要。张昌民等[54]通过回顾20年来河流沉积学的研究也指出国内河流相研究重视应用而轻视基础理论研究的问题。今后的研究也应当积极重视基础研究,贯彻从实践到理论,理论到实践的思想路线,将河流沉积学与地貌学联系起来,相互印证指导,以期进一步推进河流研究领域各学科间的交融与共同发展。
然而,本文也具有一定局限性,虽然针对两个国家典型天然河流地貌构型进行识别与研究,但对之世界繁不甚数的河流而言,只是冰山一角,且迁移构型模式的表征方法过于理想化,在实际运用中必须加以考虑具体因素具体分析。并且,由此衍生出的以下四点问题将在今后工作中加以深入研究:1)不同迁移模式之间的内在联系,2)迁移构型与垂向沉积结构之间的对应关系,3)河道迁移模式形成的主控因素,4)曲流河迁移结构中平移结构存在的争议。因此,本研究所得出的构型表征法与迁移模式对于河流的普遍应用,仍需在今后更多实践工作基础上加以深入佐证。
6 结论通过对额尔齐斯河和诺威特纳河典型河曲采用Google Earth和ACME Mapper现代卫星图像分析,结合地貌形态学与河流沉积学,对曲流河道迁移构型表征结构主要得出如下几点认识:
(1) 刻画河道迁移结构是分析其演化规律的前提。曲流河地貌形态结构表征可分细为17个静态要素、11个动态要素,深入定义了弯度指数与曲率,提出并运用了3种新构型表征参数:顺流偏转角、逆流偏转角和扩张系数。
(2) 5个表征参数S、C、Δθ、Δθ′和KM可对曲流河迁移结构做定量表征,并据此综合提炼出6种迁移结构,分别是对称扩张结构(SES)、上游旋转(逆流旋转)扩张结构(URES)、下游旋转(顺流旋转)扩张结构(DRES)、对称收敛结构(SCS)、上游旋转(逆流旋转)收敛结构(URCS)和下游旋转(顺流旋转)收敛结构(DRCS)。
(3) 通过对研究区12段河曲的精细结构表征,提出曲流河道理想化条件下迁移构型的6种常规模式和3种基本复合模式,分别是对称扩张迁移模式(SEM)、上游旋转(逆流旋转)扩张迁移模式(UREM)、下游旋转(顺流旋转)扩张迁移模式(DREM)、对称收敛迁移模式(SCM)、上游旋转(逆流旋转)收敛迁移模式(URCM)、下游旋转(顺流旋转)收敛迁移模式(DRCM)、对称扩张—收敛迁移模式(SE-CM)、上游旋转扩张—收敛迁移模式(URE-CM)和下游旋转扩张—收敛迁移模式(DRE-CM)。
(4) 河流沉积学与地下储层构型的研究方兴未艾,而跨学科结合地貌形态学理论综合表征河流演化结构的发展势在必行,在现代河流迁移构型表征预测和地下古河道过程重建的讨论中,进一步明确将来发展要结合地貌形态学规律,综合多因素动态分析河流演化过程,以辩证思想真正实现将今论古、以古鉴今的科学研究。
| [1] | Blum M, Martin J, Milliken K, et al. Paleovalley systems:insights from quaternary analogs and experiments[J]. Earth-Science Reviews, 2013, 116: 128–169. DOI: 10.1016/j.earscirev.2012.09.003 |
| [2] | Kasvi E, Laamanen L, Lotsari E, et al. Flow patterns and morphological changes in a sandy meander bend during a flood:spatially and temporally intensive ADCP measurement approach[J]. Water, 2017, 9(2): 106. DOI: 10.3390/w9020106 |
| [3] | Lin Z P, Shan J F, Chen L. Geomorphology processes of channel planform migration on meandering rivers[J]. Acta Geographica Sinica (English Edition), 2017, 91: 134–135. DOI: 10.1111/acgs.2017.91.issue-s1 |
| [4] | Lin Z P, Shan J F, Chen L. Meticulous depiction and genetic mechanism of unconformity belt structure[J]. Earth Science Research, 2017, 6(2): 19. DOI: 10.5539/esr.v6n2p19 |
| [5] | Schuurman F, Kleinhans M G, Middelkoop H. Network response to disturbances in large sand-bed braided rivers[J]. Earth Surface Dynamics, 2016, 4(1): 25–45. DOI: 10.5194/esurf-4-25-2016 |
| [6] | 胡光义, 范廷恩, 陈飞, 等. 从储层构型到"地震构型相":一种河流相高精度概念模型的表征方法[J]. 地质学报, 2017, 91 (2): 465–478. [ Hu Guangyi, Fan Ting'En, Chen Fei, et al. From reservoir architecture to seismic architecture facies:characteristic method of a high-resolution fluvial facies model[J]. Acta Geologica Sinica, 2017, 91(2): 465–478. ] |
| [7] | 胡浩. 基于砂体结构的剩余油挖潜调整措施研究[J]. 岩性油气藏, 2016, 28 (4): 113–120. [ Hu Hao. Adjustment measures of remaining oil tapping based on sand body structure[J]. Lithologic Reservoirs, 2016, 28(4): 113–120. ] |
| [8] | 穆龙新. 油藏描述的阶段性及特点[J]. 石油学报, 2000, 21 (5): 103–108. [ Mu Longxin. Stages and characteristic of reservoir description[J]. Acta Petrolei Sinica, 2000, 21(5): 103–108. DOI: 10.7623/syxb200005021 ] |
| [9] | 吴胜和, 王仲林. 陆相储层流动单元研究的新思路[J]. 沉积学报, 1999, 17 (2): 252–257. [ Wu Shenghe, Wang Zhonglin. A new method of non-marine reservoir flow unit study[J]. Acta Sedimentologica Sinica, 1999, 17(2): 252–257. ] |
| [10] | 尹太举, 张昌民, 赵红静, 等. 依据高分辨率层序地层学进行剩余油分布预测[J]. 石油勘探与开发, 2001, 28 (4): 79–82. [ Yin Taiju, Zhang Changmin, Zhao Hongjing, et al. Remaining oil distribution prediction based on high-resolution sequence stratigraphy[J]. Petroleum Exploration and Development, 2001, 28(4): 79–82. ] |
| [11] | Deb M, Das D, Uddin M. Evaluation of meandering characteristics using RS & GIS of Manu River[J]. Journal of Water Resource and Protection, 2012, 4(3): 163–171. DOI: 10.4236/jwarp.2012.43019 |
| [12] | 隋新光. 曲流河道砂体内部建筑结构研究[D]. 大庆: 大庆石油学院, 2006. [ Sui Xinguang. A study on internal architecture of channel sand in meandering river[D]. Daqing: Daqing Petroleum Institute, 2006. ] |
| [13] | Willis B J, Tang H. Three-dimensional connectivity of point-bar deposits[J]. Journal of Sedimentary Research, 2010, 80(5): 440–454. DOI: 10.2110/jsr.2010.046 |
| [14] | 薛培华. 河流点坝相储层模式概论[M]. 北京: 石油工业出版社, 1991. [ Xue Peihua. An introduction to reservoir models of point bar facies[M]. Beijing: Petroleum Industry Press, 1991. ] |
| [15] | Ielpi A, Ghinassi M. Planform architecture, stratigraphic signature and morphodynamics of an exhumed Jurassic meander plain (Scalby Formation, Yorkshire, UK)[J]. Sedimentology, 2014, 61(7): 1923–1960. DOI: 10.1111/sed.12122 |
| [16] | Leopold L B, Maddock T Jr. The hydraulic geometry of stream channels and some physiographic implications: Professional paper 252[M]. Washington D C: U. S. Government Printing Office, 1953. |
| [17] | Leopold L B, Wolman M G. River channel patterns: braided, meandering, and straight: Professional paper 282-B[M]. Washington DC: U. S. Government Printing Office, 1957. |
| [18] | Leopold L B, Bagnold R A, Wolman M G, et al. Flow resistance in sinuous or irregular channels: Professional paper 282-D[M]. Washington D C: U. S. Government Printing Office, 1960. |
| [19] | Wolman M G, Miller J P. Magnitude and frequency of forces in geomorphic processes[J]. The Journal of Geology, 1960, 68(1): 54–74. DOI: 10.1086/626637 |
| [20] | Williams G P. Bank-full discharge of rivers[J]. Water Resources Research, 1978, 14(6): 1141–1154. DOI: 10.1029/WR014i006p01141 |
| [21] | Brice J C. Evolution of meander loops[J]. GSA Bulletin, 1974, 85(4): 581–586. DOI: 10.1130/0016-7606(1974)85<581:EOML>2.0.CO;2 |
| [22] | Hooke J M. Changes in river meanders:a review of techniques and results of analyses[J]. Progress in Physical Geography, 1984, 8(4): 473–508. |
| [23] | Hooke J M. Processes of channel planform change on meandering channels in the UK[M]//Gurnell A, Petts G E. Changing River Channels. Chichester: John Wiley and Sons, 1995: 87-115. |
| [24] | Hooke J M. The distribution and nature of changes in river channel pattern[M]//Gregory K J. River Channel Changes. Chichester: John Wiley, 1997: 265-280. |
| [25] | Miall A D. Architectural-element analysis:a new method of facies analysis applied to fluvial deposits[J]. Earth-Science Reviews, 1985, 22(4): 261–308. DOI: 10.1016/0012-8252(85)90001-7 |
| [26] | Miall A D. The geology of fluvial deposits:sedimentary facies, basin analysis, and petroleum geology[M]. Berlin Heidelberg: Springer, 1996. |
| [27] | Miall A D. Fluvial depositional systems[M]. Cham: Springer, 2014. |
| [28] | Miall A D. Facies models[M]//MIALL A D. Stratigraphy: A Modern Synthesis. Cham: Springer, 2016: 161-214. |
| [29] | Ghinassi M, Nemec W, Aldinucci M, et al. Plan-form evolution of ancient meandering rivers reconstructed from longitudinal outcrop sections[J]. Sedimentology, 2014, 61(4): 952–977. DOI: 10.1111/sed.12081 |
| [30] | Wu C L, Ullan M S, Lu J, et al. Formation of point bars through rising and falling flood stages:evidence from bar morphology, sediment transport and bed shear stress[J]. Sedimentology, 2016, 63(6): 1458–1473. DOI: 10.1111/sed.12269 |
| [31] | 裘亦楠. 河流沉积学中的河型分类[J]. 石油勘探与开发, 1985, 12 (2): 72–74. [ Qiu Yinan. River type classification in fluvial sedimentology[J]. Petroleum Exploration and Development, 1985, 12(2): 72–74. ] |
| [32] | 尹燕义, 王国娟, 祁小明. 曲流河点坝储集层侧积体类型研究[J]. 石油勘探与开发, 1998, 25 (2): 37–40. [ Yin Yanyi, Wang Guojuan, Qi Xiaoming. A study on the lateral accretion body type of the meandering river point bar reservoirs[J]. Petroleum Exploration and Development, 1998, 25(2): 37–40. ] |
| [33] | 岳大力, 吴胜和, 刘建民. 曲流河点坝地下储层构型精细解剖方法[J]. 石油学报, 2007, 28 (4): 99–103. [ Yue Dali, Wu Shenghe, Liu Jianmin. An accurate method for anatomizing architecture of subsurface reservoir in point bar of meandering river[J]. Acta Petrolei Sinica, 2007, 28(4): 99–103. DOI: 10.7623/syxb200704020 ] |
| [34] | 周银邦, 吴胜和, 岳大力, 等. 点坝内部侧积层倾角控制因素分析及识别方法[J]. 中国石油大学学报(自然科学版), 2009, 33 (2): 7–11. [ Zhou Yinbang, Wu Shenghe, Yue Dali, et al. Controlling factor analysis and identification method of lateral accretion shale beddings angle in point bar[J]. Journal of China University of Petroleum, 2009, 33(2): 7–11. ] |
| [35] | 单敬福, 张吉, 赵忠军, 等. 地下曲流河点坝砂体沉积演化过程分析:以吉林油田杨大城子油层第23小层为例[J]. 石油学报, 2015, 36 (7): 809–819. [ Shan Jingfu, Zhang Ji, Zhao Zhongjun, et al. Analysis of sedimentary and evolution process for underground meandering river point bar:A case study from No.23 thin layer of Yangdachengzi oil reservoir in Jilin oilfield[J]. Acta Petrolei Sinica, 2015, 36(7): 809–819. DOI: 10.7623/syxb201507005 ] |
| [36] | Lin Z P. Channel planform migration architecture of meandering rivers[J]. Journal of Geology & Geophysics, 2017, 6(S3): 63. |
| [37] | Gilvear D, Winterbottom S, Sichingabula H. Character of channel planform change and meander development:Luangwa River, Zambia[J]. Earth Surface Processes and Landforms, 2000, 25(4): 421–436. DOI: 10.1002/(ISSN)1096-9837 |
| [38] | Hooke J M. Magnitude and distribution of rates of river bank erosion[J]. Earth Surface Processes and Landforms, 1980, 5(2): 143–157. DOI: 10.1002/(ISSN)1931-8065 |
| [39] | Wu C L, Bhattacharya J P, Ullah M S. Paleohydrology and 3D facies architecture of ancient point bars, ferron sandstone, notom delta, South-Central Utah, U.S.A.[J]. Journal of Sedimentary Research, 2015, 85(4): 399–418. DOI: 10.2110/jsr.2015.29 |
| [40] | Ghinassi M, Ielpi A, Aldinucci M, et al. Downstream-migrating fluvial point bars in the rock record[J]. Sedimentary Geology, 2016, 334: 66–96. DOI: 10.1016/j.sedgeo.2016.01.005 |
| [41] | 吴胜和, 岳大力, 刘建民, 等. 地下古河道储层构型的层次建模研究[J]. 中国科学D辑:地球科学, 2008, 38 (增刊1): 111–121. [ Wu Shenghe, Yu Dali, Liu Jianmin, et al. Hierarchy modeling of subsurface palaeochannel reservoir architecture[J]. Science in China Series D:Earth Sciences, 2008, 38(Suppl.1): 111–121. ] |
| [42] | 单敬福, 李占东, 葛雪, 等. 一种古沉积期曲流河道演化过程重建方法[J]. 中国矿业大学学报, 2015, 44 (5): 843–852. [ Shan Jingfu, Li Zhandong, Ge Xue, et al. A method of reconstructing evolutionary process of meandering channel in paleo-sedimentary period[J]. Journal of China University of Mining & Technology, 2015, 44(5): 843–852. ] |
| [43] | Asahi K, Shimizu Y, Nelson J, et al. Numerical simulation of river meandering with self-evolving banks[J]. Journal of Geophysical Research:Earth Surface, 2013, 118(4): 2208–2229. DOI: 10.1002/jgrf.20150 |
| [44] | Schuurman F. Bar and channel evolution in meandering and braiding rivers using physics-based modeling[D]. Utrecht: Utrecht University, 2015. |
| [45] | Rousseau Y Y, Biron P M, van De Wiel M J. Sensitivity of simulated flow fields and bathymetries in meandering channels to the choice of a morphodynamic model[J]. Earth Surface Processes and Landforms, 2016, 41(9): 1169–1184. DOI: 10.1002/esp.v41.9 |
| [46] | 冯增昭. 中国沉积学[M]. 2版. 北京: 石油工业出版社, 2013. [ Feng Zengzhao. Sedimentology of China[M]. 2nd ed. Beijing: Petroleum Industry Press, 2013. ] |
| [47] | 何幼斌, 王文广. 沉积岩与沉积相[M]. 北京: 石油工业出版社, 2008. [ He Youbin, Wang Wenguang. Sedimentary rocks and sedimentary facies[M]. Beijing: Petroleum Industry Press, 2008. ] |
| [48] | 朱筱敏. 沉积岩石学[M]. 4版. 北京: 石油工业出版社, 2008. [ Zhu Xiaomin. Sedimentary petrology[M]. 4th ed. Beijing: Petroleum Industry Press, 2008. ] |
| [49] | Bluck B J. Sedimentation in the meandering river endrick[J]. Scottish Journal of Geology, 1971, 7(2): 93–138. DOI: 10.1144/sjg07020093 |
| [50] | 石书缘, 胡素云, 冯文杰, 等. 基于Google Earth软件建立曲流河地质知识库[J]. 沉积学报, 2012, 30 (5): 869–878. [ Shi Shuyuan, Hu Suyun, Feng Wenjie, et al. Building geological knowledge database based on google earth software[J]. Acta Sedimentologica Sinica, 2012, 30(5): 869–878. ] |
| [51] | Hartley A J, Weissmann G S, Nichols G J, et al. Large distributive fluvial systems:characteristics, distribution, and controls on development[J]. Journal of Sedimentary Research, 2010, 80(2): 167–183. DOI: 10.2110/jsr.2010.016 |
| [52] | Weissmann G S, Hartley A J, Nichols GJ, et al. Fluvial form in modern continental sedimentary basins:distributive fluvial systems[J]. Geology, 2010, 38(1): 39–42. DOI: 10.1130/G30242.1 |
| [53] | 张昌民, 尹太举, 喻辰, 等. 基于过程的分流平原高弯河道砂体储层内部建筑结构分析:以大庆油田萨北地区为例[J]. 沉积学报, 2013, 31 (4): 653–662. [ Zhang Changmin, Yin Taiju, Yu Chen, et al. Reservoir architectural analysis of meandering channel sandstone in the delta plain based on the depositional process[J]. Acta Sedimentologica Sinica, 2013, 31(4): 653–662. ] |
| [54] | 张昌民, 张尚锋, 李少华, 等. 中国河流沉积学研究20年[J]. 沉积学报, 2004, 22 (2): 183–192. [ Zhang Changmin, Zhang Shangfeng, Li Shaohua, et al. Advances in Chinese fluvial sedimentology from 1983 to 2003[J]. Acta Sedimentologica Sinica, 2004, 22(2): 183–192. ] |
 2018, Vol. 36
2018, Vol. 36



