针对多用户无线供电通信网络系统中的交叉耦合干扰问题,提出了一种基于时间反演技术联合优化上、下行时间分配和功率分配方案,以最大化上行加权和速率.利用时间反演特有的空时聚焦性抑制交叉耦合干扰;然后建立优化模型,将难以求解的加权和速率问题转化为最小均方误差问题;最后通过分级逐次优化变量,分别求出功率和时间的最优解.仿真结果表明,在引入时间反演技术抑制系统的交叉耦合干扰后,系统的平均加权和速率明显提升.
A jointly optimize time and power allocation in uplink and downlink scheme combined with time reversal technique is proposed to solve the cross-link interference problem in multi-user wireless powered communication networks and maximize the uplink weighted sum-rate.Using the unique time-space focusing of time reversal to suppress the cross-link interference firstly, an optimization model is then established, thus the non-convex weighted sum-rate problem transformed into weighted minimum mean square error problem is solved.The optimal solution of power and time can be obtained separately by grading optimize variables sequentially.Simulations show that the system average sum-rate significantly improved after introducing the time reversal technique to suppress the cross-link interference.
无线供电通信网络(WPCN,wireless powered communication networks)可利用射频能量传输技术,通过将射频信号向低功耗的物联网终端传输能量来实现系统的“自我可持续”[1-2].在WPCN中,无线通信设备将下行捕获的射频能量信号用于上行链路的信息传输.
Ju等[3]于2014年提出基于射频能量传输的WPCN系统,在单小区中,通过时分多址接入(TDMA,time division multiple access)方式避免了用户间干扰并提出了基于用户吞吐量最大化的时间分配方案.在此基础上,Liu等[4]提出了空分多址接入(SDMA,space division multiple access)方式,通过对下行链路波束赋形以及对上行链路功率分配,最大化用户的最小吞吐量. Lee等[5]在单个小区场景下,利用预编码矩阵对多输入多输出(MIMO,multiple input multiple output)WPCN系统进行上、下行传输,并利用逐次干扰消除技术进行信息解码,以实现系统吞吐量最大. Kim等[6]将WPCN应用到了多小区环境中,在分布式大规模MIMO系统中考虑了小区间干扰,并提出了使系统能效最大化的优化算法. Kim等[7]将WPCN应用到N个用户的干扰信道中. Rezaei等[8]在干扰信道下,分析了MIMO WPCN系统的吞吐量优化问题.
针对多用户干扰信道下的WPCN系统,在异步情况下会产生交叉耦合干扰的问题,Kim等[7]虽然提出了一种基于TDMA的分配方案以避免交叉耦合干扰的产生,但其方案在相同条件下系统的和速率有所降低.基于此,采用时间反演技术抑制交叉耦合干扰,构建了包含多维时间参数及上、下行功率分配的优化模型,最后通过分级逐次优化,求出时间和功率的最优解.同时基于所提优化模型,分析了小区个数、发射功率等参数与系统加权和速率的关系,证明了所提方案可有效抑制交叉耦合干扰,提升系统加权和速率.
1 系统模型考虑一个具有N个用户干扰信道下的WPCN系统,其中第j个混合接入点(H-AP,hybrid access point)为第j个小区的一个用户服务,j∈{1, 2, …, N}.在WPCN系统中,H-AP首先向用户进行无线能量传输(WET,wireless energy transfer),用户接收到能量后将其储存在可蓄电电池中.与传统WPCN系统不同的是,在H-AP向用户发送WET信号后,会继续发送时间反演探测信号,用户在接收到探测信号后,再上行进行无线信息传输(WIT,wireless information transfer).假定所有的H-AP和用户都是单天线并且工作在同一频段内.
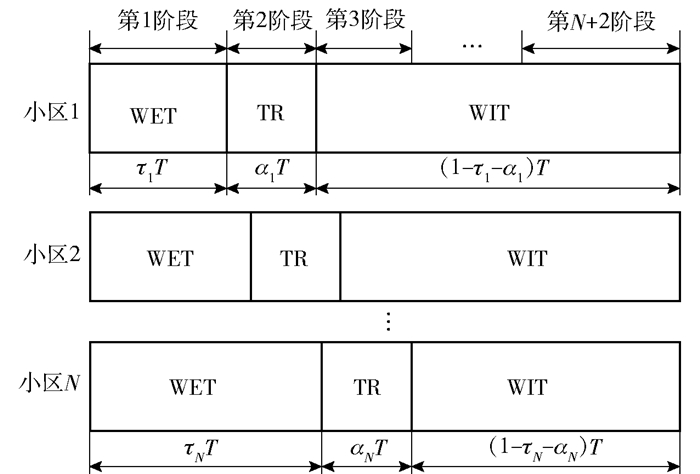
在实际情况中,各个小区发送WET信号和WIT信号的时间可能不是同步的,因此,不对称的时间分配会导致交叉耦合干扰的产生[9].为抑制这种交叉耦合干扰,在原有的收获-传输(HTT,harvest then transfer)协议基础上,划分了一个时间反演探测阶段,如图 1所示.
|
图 1 各个小区时间分配框图 |
把一个时间周期T分成了N+2个阶段,τj、αj和1-τj-αj分别表示第j个小区的下行WET传输时间、时间反演探测时间和上行WIT传输时间.
假定所有小区的信道状态信息已知,且具有信道互易性,令τ1≤τ2≤…≤τN,且α1=α2=…=αN.在第1个阶段0≤t≤τ1,所有的H-AP都在进行下行WET信号传输,用户进行能量收集.在多径信道下,定义第j个H-AP和第i个用户之间的下行信道冲激响应为hij(t),i, j∈{1, 2, …, N},对其建立抽头延迟线模型,有
| $ {h_{ij}}(t) = \sum\limits_{l = 0}^{L - 1} {{\delta _{ij,l}}} \delta (t - {\sigma _{ij,l}}),1 \le l \le L $ | (1) |
其中:δij, l为多径信道的第l条多径的幅度,σij, l为多径信道的第l条多径的时延.当hij(t)离散化为hij∈ CL×1时
| $ {h_{ij}} = {\{ {h_{ij}}[0],{h_{ij}}[1], \cdots ,{h_{ij}}[L - 1]\} ^{\rm{T}}} $ | (2) |
对信道冲激响应进行时域离散化操作有E(hij[l])=0和E(|hij[l]|2)=δij, l2.
令riuser[n]表示第i个用户在第n个阶段接收到的信号,n∈{1, 2, …, N+1},因此,用户i在n=1阶段时接收到的信号为
| $ \begin{array}{*{20}{l}} {r_i^{{\rm{ user }}}[1] = \sum\limits_{j = 1}^N {\sum\limits_{l = 0}^{L - 1} {\sqrt {{p_{d,j}}[1]} } } {h_{ij}}[l]{x_{d,j}}[1] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z_i^{{\rm{ user }}}[1],\forall i} \end{array} $ | (3) |
其中:pd, j[n]表示第j个H-AP在第n个阶段下行传输功率;xd, j[n]表示第j个H-AP在第n个阶段传输的WET信号,且E[|xd, j[n]|2]=1;ziuser[n]表示第i个用户的复高斯白噪声.因此,在第1阶段用户i收集到的能量Ei, 1为
| $ {E_{i,1}} = \eta {\tau _1}\sum\limits_{j = 1}^N {\sum\limits_{l = 0}^{L - 1} {{p_{d,j}}} } [n]|{h_{ij}}[l]{|^2},\forall i $ | (4) |
其中η表示能量收集转换效率.与pd, j[n]相比,式(3)中的白噪声功率可忽略不计.
当n=2阶段时,j∈{1, 2, …, N}个H-AP中开始有部分H-AP下行发送探测信号,获取目标用户的信道状态信息,此时目标用户端对信号进行时间反演预处理,接着目标用户上行沿相同信道传输信号,信号会在对应的H-AP处聚焦,最后进行归一化处理.因此,经时间反演操作后,第i个用户和第j个H-AP之间的上行等效信道为
| $ {h_{ij}} = {\{ h_{ij}^{{\rm{tr}}}[0],h_{ij}^{{\rm{tr}}}[1], \cdots ,h_{ij}^{{\rm{tr}}}[L - 1]\} ^{\rm{T}}} $ | (5) |
其中hijtr的每个抽头值可以写为
| $ h_{ij}^{{\rm{tr}}}[l] = \frac{{h_{ij}^*[L + 1 - l]}}{{\sqrt {E\left[ {\sum\limits_{l = 1}^{L - 1} {{{\left\| {{h_{ij}}[l]} \right\|}^2}} } \right]} }} $ | (6) |
剩余的n∈{3, …, N}会产生交叉耦合干扰.当第j2∈{n1+1, n1+2,…,N}个H-AP发送下行WET信号时,第j1∈{n0+1, n0+2,…,n1}个H-AP发送TR探测信号,而剩余的j0∈{1, 2,…, n0}个H-AP会接收到来自第i个用户的WIT信息.
rjH-AP[n]表示第j个H-AP,j∈{1, 2, …, n0},在第n个阶段收到的信号可表示为
| $ \begin{array}{*{20}{c}} {r_j^{{\rm{H - AP}}}[n] = \sum\limits_{l = 0}^{2L - 2} {\sqrt {{p_{u,i}}[n]} } ({h_{ij}}*h_{ij}^{{\rm{tr}}})[l]{x_{u,i}}[n]{|_{(i = j)}} + }\\ {\sum\limits_{i = 1,i \ne j}^{{n_0}} {\sum\limits_{l = 0}^{L - 1} {\sqrt {{p_{u,i}}[n]} } } h_{ij}^{{\rm{tr}}}[l]{x_{u,i}}[n] + }\\ {\sum\limits_{k = {n_0} + 1}^{{n_1}} {\sum\limits_{l = 0}^{L - 1} {\sqrt {{p_{{\rm tr},k}}[n]} {g_{jk}}[l]{x_{{\rm tr},k}}[n] + } } }\\ {\sum\limits_{k = {n_1} + 1}^N {\sum\limits_{l = 0}^{L - 1} {\sqrt {\beta {p_{d,k}}[n]} } {g_{jk}}[l]{x_{d,k}}[n] + } }\\ {z_j^{{\rm{H - AP}}}[n]} \end{array} $ | (7) |
其中:pu, i[n]表示第i个用户在第n个阶段上行传输的功率;xu, i[n]表示WIT信号且E[|xu, i[n]|2]=1;β是WET信号的衰减系数;gjk表示第j个H-AP和第k个H-AP的信道相关性;zjH-AP[n]是第j个H-AP的复高斯白噪声,其均值为0,方差为σ2.
第j个H-AP,j∈{1, 2, …, n0},在第n个阶段的可达信息速率如式(8)(9)所示.
| $ {R_j}[n] = ({\tau _n} - {\tau _{n - 1}})]{\rm{lb}}(1 + {A_j}) $ | (8) |
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{A_j} = {p_{u,i}}[n]|{h_{ij}}[L - 1]{|^2}|h_{ij}^{{\rm{tr}}}[L - 1]{|^2}{|_{(i = j)}}/({\sigma ^2} + }\\ {\sum\limits_{m = 0,m \ne L - 1}^{2L - 2} {{p_{u,i}}} [n]|{h_{ij}}[m]{|^2}|h_{ij}^{{\rm{tr}}}[m]{|^2}{|_{(i = j)}} + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} {\sum\limits_{i = 1,i \ne j}^{{n_0}} {\sum\limits_{l = 0}^{L - 1} {{p_{u,i}}} } [n]|h_{ij}^{\rm tr}[l]{|^2} + }\\ {\sum\limits_{k = {n_0} + 1}^{{n_1}} {\sum\limits_{l = 0}^{L - 1} {{p_{{\rm{tr}},k}}} } [n]|{g_{jk}}[l]{|^2} + }\\ {\sum\limits_{k = {n_1} + 1}^N {\sum\limits_{l = 0}^{L - 1} \beta } {p_{d,k}}[n]|{g_{jk}}[l]{|^2}} \end{array} \end{array} $ | (9) |
此时,用户i仍在第n个阶段收集能量,i∈{n1+1, n1+2, …, N},其接收到的信号为
| $ \begin{array}{l} r_i^{{\rm{user}}}[n] = \sum\limits_{k = {n_1} + 1}^N {\sum\limits_{l = 0}^{L - 1} {\sqrt {{p_{d,k}}[n]} } } {h_{ik}}[l]{x_{d,k}}[n] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} {\sum\limits_{k = {n_0} + 1,k \ne i}^{{n_1}} {\sum\limits_{l = 0}^{L - 1} {\sqrt {{p_{{\rm tr},k}}[n]} } } g_{ik}^{{\rm{user}}}[l]{x_{{\rm tr},k}}[n] + }\\ {\sum\limits_{k = 1,k \ne i}^{{n_0}} {\sum\limits_{l = 0}^{L - 1} {\sqrt {{p_{u,k}}[n]} } } g_{ik}^{{\rm{user}}}[l]{x_{u,k}}[n] + }\\ {z_i^{{\rm{user}}}[n]} \end{array} \end{array} $ | (10) |
其收集的能量表示为
| $ \begin{array}{*{20}{c}} {{E_{i,n}} = \eta ({\tau _n} - {\tau _{n - 1}})\left( {\sum\limits_{k = {n_1} + 1}^N {\sum\limits_{l = 0}^{L - 1} {{p_{d,k}}} } [n]|{h_{ik}}[l]{|^2} + } \right.}\\ {\sum\limits_{\begin{array}{*{20}{c}} {k = {n_0} + 1}\\ {k \ne i} \end{array}}^{{n_1}} {\sum\limits_{l = 0}^{L - 1} {{p_{{\rm{tr}},k}}} } [n]|g_{ik}^{{\rm{user}}}[l]{|^2} + }\\ {\left. {\sum\limits_{\begin{array}{*{20}{c}} {k = 1}\\ {k \ne i} \end{array},}^{{n_0}} {\sum\limits_{l = 0}^{L - 1} {{p_{u,k}}} } [n]|g_{ik}^{{\rm{user}}}[l]{|^2}} \right)} \end{array} $ | (11) |
当n=N+2,所有的用户上行发送信息,第j个H-AP接收到的信息为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r_j^{{\rm{H - AP}}}[N + 2] = \\ \sum\limits_{l = 0}^{L - 1} {\sqrt {{p_{u,i}}[N + 2]} } ({h_{ij}}*h_{ij}^*)[l]{x_{u,i}}[N + 2]{|_{(i = j)}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1,k \ne j}^N {\sum\limits_{l = 0}^{L - 1} {\sqrt {{p_{u,k}}[N + 2]} } } {h_{kj}}[l]{x_{u,k}}[N + 2] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z_j^{{\rm{H - AP}}}[N + 2] \end{array} $ | (12) |
第j个H-AP在第(N+2)个阶段的可达信息速率为
| $ \begin{array}{*{20}{c}} {{R_j}[N + 2] = (1 - {\tau _j} - {\alpha _j}) \times }\\ {{\rm{lb}}\left( {1 + \frac{{{p_{u,i}}[N + 2]|{h_{ij}}[L - 1]{|^2}|h_{ij}^{{\rm{tr}}}[L - 1]{|^2}{|_{(i = j)}}}}{{{B_j}}}} \right)} \end{array} $ | (13) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {B_j} = \sum\limits_{k = 1,k \ne j}^N {\sum\limits_{l = 0}^{L - 1} {{p_{u,k}}} } [N + 2]|{h_{kj}}[l]{|^2} + \\ \sum\limits_{m = 0,m \ne L - 1}^{2L - 2} {{p_{u,i}}} [N + 2]|{h_{ij}}[m]{|^2}|h_{ij}^{{\rm{tr}}}[m]{|^2}{|_{(i = j)}} + {\sigma ^2} \end{array} $ | (14) |
对于用户i而言,其总可达速率为
各个小区时间反演探测时长相同,因此各个小区时间反演功率分配变量{ptr, j[n]}相等,且需要满足距离最远的小区可以接收到探测信号.
联合时间变量{τi, αi}、下行功率变量{pd, j[n]}及上行功率分配变量{pu, i[n]}最大化系统加权速率和问题可描述为
| $ \begin{array}{l} \mathop {{\rm{max}}}\limits_{\begin{array}{*{20}{c}} {\{ {\tau _i},{\alpha _i}\} }\\ {\{ {p_{u,i}}[n]\} }\\ {\{ {p_{d,j}}[n]\} } \end{array}} R(\{ {\tau _i},{\alpha _i}\} ,\{ {p_{u,i}}[n]\} ,\{ {p_{d,j}}[n]\} ) \buildrel \Delta \over = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^N {\sum\limits_{n = i + 2}^{N + 2} {{\psi _i}} } {R_i}[n]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1}}:\sum\limits_{n = i + 2}^{N + 2} {({\tau _n} - {\tau _{n - 1}})} {p_{u,i}}[n] \le {E_i},\quad \forall i,\\ \begin{array}{*{20}{l}} {{\rm{C2}}:{p_{d,j}}[n] \le {p_{{\rm{ peak }},j}},\forall j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} n \in \{ 1,2, \cdots ,j\} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C3}}:{\alpha _i} \ge {s_{{\rm{max}}}}/c,} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C4}}:{\tau _1} \le {\tau _2} \le \cdots \le {\tau _N} \le 1,{\tau _0} = 0,{\tau _{N + 2}} = 1 \end{array} $ | (15) |
其中:ψi表示系统中用户i的加权系数;C1表示上行传输功率约束,即用户发送信息所消耗的能量不能多于接收到的能量;ppeak为功率的峰值;smax为用户到H-AP的最远距离;c为信号传输速率.
2.2 问题求解由于目标函数及约束条件C1的非凸性,式(15)的最优解不能直接求出,因此,利用一种逐次分级优化的方法可以求得式(15)的局部最优解.通过将WRS问题转换为WMMSE问题[10],先固定{τi, αi},更新{pu, i[n], pd, j[n]},然后固定{pu, i[n], pd, j[n]},通过内点法计算{τi, αi}.
首先固定变量{τi, αi},然后引入2个新的变量qd, j[n]=(τn-τn-1)pd, j[n](∀j且n∈{1, 2, …, j})和qu, i[n]=(τn-τn-1)pu, i[n](∀i且n∈{i+2, …, N+2}).令{Wi, n}表示第i个用户在第n个阶段的正加权变量,{Ui, n}表示第i个用户在第n个阶段的MMSE接收器,此时式(15)等价于下面的WMMSE问题:
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_{\begin{array}{*{20}{c}} {\{ {W_{i,n}}\} ,\{ {U_{i,n}}\} }\\ {\{ {p_{u,i}}[n]\} ,\{ {p_{d,j}}[n]\} } \end{array}} \sum\limits_{n = 3}^{N + 2} {\sum\limits_{i = 1}^{{n_0}} {{\psi _i}} } ({\tau _n} - {\tau _{n - 1}})({W_{i,n}}{e_{i,n}} - {\rm{lb}}{W_{i,n}})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1}}:\sum\limits_{n = i + 2}^{N + 2} {{q_{u,i}}} [n] \le {E_i},\forall i,\\ {\rm{C2}}:{q_{d,j}}[n] \le ({\tau _n} - {\tau _{n - 1}}){p_{{\rm{peak}},j}},\forall j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} n \in \{ 1,2, \cdots ,j\} \end{array} $ | (16) |
其中:ei, n({Ui, n}, {qu, i[n]}, {qd, j[n]})代表均方误差[10];n∈{i+2, …N+2},表示为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {e_{i,n}}(\{ {U_{i,n}}\} ,\{ {q_{u,i}}[n]\} ,\{ {q_{d,j}}[n]\} ) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left| {\frac{{{\omega _1}U_{i,n}^*}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} - 1}}} \right|^2} + {\left| {\frac{{\sum\limits_{{l^\prime } = 0,{l^\prime } \ne L - 1}^{2L - 2} {{\omega _2}} U_{i,n}^*}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}} \right|^2} + \\ \sum\limits_{k = 1,k \ne i}^{{n_0}} {{{\left| {\frac{{\sum\limits_{l = 0}^{L - 1} {{\omega _3}} U_{i,n}^*}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}} \right|}^2}} + \sum\limits_{k = {n_0} + 1}^{{n_1}} {{{\left| {\frac{{\sum\limits_{l = 0}^{L - 1} {{\omega _4}} U_{i,n}^*}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}} \right|}^2}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = {n_1} + 1}^N {{{\left| {\frac{{\sum\limits_{l = 0}^{L - 1} {{\omega _5}} U_{i,n}^*}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}} \right|}^2}} + {\sigma ^2}|{U_{i,n}}{|^2} \end{array} $ | (17) |
其中:
对于式(17)中的目标函数而言,优化变量{Wi, n},{Ui, n}和{qu, i[n], qd, j[n]}都是凸的,因此通过逐次分级,优化固定其余2个变量,可以求出剩下一个变量的最优值.由此可以得到局部优化的MMSE接收变量{Ui, nopt}和权重{Wi, nopt}为
| $ U_{i,n}^{{\rm{opt}}} = \frac{{\sqrt {{q_{u,i}}[n]} ({h_{i,i}}*h_{i,i}^{{\rm{tr}}})[L - 1]}}{{\frac{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}{{{C_{i,n}}}}}} $ | (18) |
| $ \begin{array}{*{20}{c}} {{C_{i,n}} = \sum\limits_{l = 0}^{2L - 2} {\frac{{{q_{u,i}}[n]|{h_{i,i}}{|^2}|h_{i,i}^{{\rm{tr}}}{|^2}}}{{{\tau _n} - {\tau _{n - 1}}}}} + }\\ {\sum\limits_{k = 1,k \ne i}^{{n_0}} {\sum\limits_{l = 0}^{L - 1} {\frac{{{q_{u,k}}[n]|{h_{ik}}[l]{|^2}}}{{{\tau _n} - {\tau _{n - 1}}}}} } + }\\ {\sum\limits_{k = {n_0} + 1}^{{n_1}} {\sum\limits_{l = 0}^{L - 1} {\frac{{{q_{{\rm{tr}}}}[n]{{\left| {{g_{ik}}[l]} \right|}^2}}}{{{\tau _n} - {\tau _{n - 1}}}}} } + }\\ {\sum\limits_{k = {n_1} + 1}^N {\sum\limits_{l = 0}^{L - 1} {\frac{{\beta {q_{d,k}}[n]|{g_{ik}}[l]{|^2}}}{{{\tau _n} - {\tau _{n - 1}}}}} } + {\sigma ^2}} \end{array} $ | (19) |
| $ W_{i,n}^{{\rm{opt}}} = e_{i,n}^{ - 1},\forall i{\rm{ 且 }}n \in \{ i + 2, \cdots ,N + 1\} $ | (20) |
将{Ui, nopt}和{Wi, nopt}的值代入目标函数式(16),可以看出式(15)和式(16)是等价的,因此式(15)中的优化变量{pu, i[n], pd, j[n]}可以通过求式(16)中的优化变量{qu, i[n], qd, j[n]}得到.将已经得到的{Ui, nopt}和{Wi, nopt}代入式(16)计算可得
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_{\{ {q_{u,i}}[n]\} ,\{ {q_{d,j}}[n]\} } f(\{ {q_{u,i}}[n]\} ,\{ {q_{d,j}}[n]\} )\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1 }}:\sum\limits_{n = i + 2}^{N + 1} {{q_{u,i}}} [n] \le {E_i},\forall i,}\\ {{\rm{C2}}{\kern 1pt} {\rm{:}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {q_{d,j}}[n] \le ({\tau _n} - {\tau _{n - 1}}){p_{{\rm{ peak }},j}},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} n \in \{ 1,2, \cdots ,j\} } \end{array} \end{array} $ | (21) |
其中
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {f(\{ {q_{u,i}}[n]\} ,\{ {q_{d,j}}[n]\} ) \buildrel \Delta \over = }\\ {\sum\limits_{n = 3}^{N + 2} {\sum\limits_{i = 1}^{{n_0}} {{\psi _i}} } ({\tau _n} - {\tau _{n - 1}})W_{i,n}^{{\rm{opt}}} \times } \end{array}\\ \left( {{{\left| {\frac{{{\omega _1}{{(U_{i,n}^{{\rm{opt}}})}^*}}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }} - 1} \right|}^2} + {{\left| {\frac{{\sum\limits_{{l^\prime } = 0,{l^\prime } \ne L - 1}^{2L - 2} {{\omega _2}} {{(U_{i,n}^{{\rm{opt}}})}^*}}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}} \right|}^2} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1,k \ne i}^{{n_0}} {{{\left| {\frac{{\sum\limits_{l = 0}^{L - 1} {{\omega _3}} {{(U_{i,n}^{{\rm{opt}}})}^*}}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}} \right|}^2}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = {n_0} + 1}^{{n_1}} {{{\left| {\frac{{\sum\limits_{l = 0}^{L - 1} {{\omega _4}} {{(U_{i,n}^{{\rm{opt}}})}^*}}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}} \right|}^2}} + \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = {n_1} + 1}^N {{{\left| {\frac{{\sum\limits_{l = 0}^{L - 1} {{\omega _5}} {{(U_{i,n}^{{\rm{opt}}})}^*}}}{{\sqrt {{\tau _n} - {\tau _{n - 1}}} }}} \right|}^2}} } \right) \end{array} $ | (22) |
式(21)可由拉格朗日对偶法求得最优解
| $ \begin{array}{*{20}{l}} {\mathscr{L} = f(\{ {q_{u,i}}[n]\} ,\{ {q_{d,j}}[n]\} ) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^N {{\mu _i}} \left( {\sum\limits_{n = i + 2}^{N + 1} {{q_{u,i}}} [n] - {E_i}} \right)} \end{array} $ | (23) |
其中μi为关于约束条件C1的非负对偶变量,对偶函数为
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g(\{ {\mu _i}\} ) \buildrel \Delta \over = \mathop {{\rm{min}}}\limits_{\{ {q_{u,i}}[n],{q_{d,j}}[n]\} } \mathscr{L}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1}}:{q_{d,j}}[n] \le ({\tau _n} - {\tau _{n - 1}}){p_{{\rm{ peak }},j}},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} n \in \{ 1,2, \cdots ,j\} } \end{array} $ | (24) |
为了得到对偶函数g({μi})的解,需要先求出式(23)中变量{qu, i[n], qd, j[n]}的值.而变量{qu, i[n], qd, j[n]}的值可以通过分别对其求导,并令导数为0得到.因此,有
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{q_{u,i}}[n] = }\\ {({\psi _i}\sqrt {{\tau _n} - {\tau _{n - 1}}} W_{i,n}^{{\rm{opt}}}{\rm{Re}} \{ U_{i,n}^{{\rm{opt}}}({h_{ii}}*h_{ii}^{{\rm{tr}}})[L - 1]\} /} \end{array}\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{\mu _i} + \sum\limits_{s = 1}^{{n_0}} {\sum\limits_{l = 0}^{2L - 2} {{\psi _s}} } W_{s,n}^{{\rm{opt}}}|U_{s,n}^{{\rm{opt}}}{|^2}|({h_{ii}}*h_{ii}^{{\rm{tr}}})[l]{|^2} + } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{s = {n_0} + 1}^{{n_1}} {\sum\limits_{l = 0}^{L - 1} {{\psi _s}} } W_{s,n}^{{\rm{opt}}}|U_{s,n}^{{\rm{opt}}}{|^2}|h_{is}^{{\rm{tr}}}[l]{|^2} - } \end{array}\\ {\left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \eta {\kern 1pt} \sum\limits_{s = {n_1} + 1}^N {\sum\limits_{l = 0}^{L - 1} {{\mu _s}} } |g_{si}^{{\rm{ user }}}{|^2}} \right)} \right)^2} \end{array} $ | (25) |
| $ {q_{d,j}}[n] = \left\{ {\begin{array}{*{20}{l}} {({\tau _n} - {\tau _{n - 1}}){p_{{\rm{ peak }},j}},}&{{\rm{ if }}{\kern 1pt} {{\tilde q}_{d,j}}[n] \le 0}\\ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{else }}}&{} \end{array}} \right. $ | (26) |
其中Re{ ·}表示复数的实部,其中
| $ \begin{array}{*{20}{l}} {{{\tilde q}_{d,j}}[n] = \sum\limits_{k = 1}^{{n_0}} {\sum\limits_{l = 0}^{L - 1} {{\psi _k}} } \beta W_{k,n}^{{\rm{ opt }}}|U_{k,n}^{{\rm{ opt }}}{|^2}|{g_{kj}}[l]{|^2} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \eta \sum\limits_{k = {n_1} + 1}^N {\sum\limits_{l = 0}^{L - 1} {{\mu _k}} } |{h_{kj}}[l]{|^2}} \end{array} $ | (27) |
由式(25)、式(26)结合内点法可以求出式(24)的解.因此,式(21)的最优解{qu, iopt}和{qd, jopt}可通过将μiopt分别代入式(25)、式(26)求出.
当求出最优解{qu, iopt}和{qd, jopt}后,代入式(15)可以求出时间变量{τi, αi}的解,此时问题变为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{max}}}\limits_{{\tau _i},{\alpha _i}} R({\tau _i},{\alpha _i}) \buildrel \Delta \over = \sum\limits_{i = 1}^N {\sum\limits_{n = i + 2}^{N + 2} {{\psi _i}} } {R_i}[n]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1}}:{\alpha _i} \ge \frac{{{s_{{\rm{max}}}}}}{c},\\ {\kern 1pt} {\rm{C2}}:{\tau _1} \le {\tau _2} \le \cdots \le {\tau _N} \le 1,{\tau _0} = 0,{\tau _{N + 2}} = 1 \end{array} $ | (28) |
为使问题简化,令ε =[ε1, ε2, …, εN+1]T,其中εi=τi+1-τi,此时式(28)变为
| $ \begin{array}{*{20}{l}} {\mathop {{\rm{max}}}\limits_{{\alpha _i},\varepsilon } \sum\limits_{i = 1}^N {\sum\limits_{n = i + 2}^{N + 2} {{\psi _i}} } {\varepsilon _{n - 1}}{g_1}(\mathit{\boldsymbol{\varepsilon }})}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{C1}}:{\alpha _i} \ge \frac{{{s_{{\rm{max}}}}}}{c}}\\ {\quad {\rm{ C2 }}:\sum\limits_{n = 1}^{N + 1} {{\varepsilon _n}} \le 1} \end{array} $ | (29) |
其中g1(ε)如式(30)、式(31)所示.式(29)为二次规划问题,可通过内点法得到最优解.
| $ {g_1}(\mathit{\boldsymbol{\varepsilon }}) = {\rm{lb}} \left( {1 + \frac{{{q_{u,i}}[n]|({h_{ii}}*h_{ii}^{{\rm{tr}}})[L - 1]{|^2}}}{{{\varepsilon _{n - 1}}D}}} \right) $ | (30) |
| $ \begin{array}{l} D = \frac{{\sum\limits_{{l^\prime } = 0,{l^\prime } \ne L - 1}^{2L - 2} {{q_{u,i}}} [n]|({h_{ii}}*h_{ii}^{{\rm{tr}}})[{l^\prime }]{|^2}}}{{{\varepsilon _{n - 1}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\sum\limits_{k = 1,k \ne i}^{{n_0}} {\sum\limits_{l = 0}^{L - 1} {{q_{u,k}}} } [n]|h_{ik}^{{\rm{tr}}}[l]{|^2}}}{{{\varepsilon _{n - 1}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\sum\limits_{k = {n_0} + 1}^{{n_1}} {\sum\limits_{l = 0}^{L - 1} {{q_{\rm tr}}} } [n]|{g_{ik}}[l]{|^2}}}{{{\varepsilon _{n - 1}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\sum\limits_{k = {n_1} + 1}^N {\sum\limits_{l = 0}^{L - 1} \beta } {q_{d,k}}[n]|{g_{ik}}[l]{|^2}}}{{{\varepsilon _{n - 1}}}} + {\sigma ^2} \end{array} $ | (31) |
综合上述的功率分配方案和时间分配方案,为解决式(15),求得最大加权和速率,将功率变量和时间变量的值不断迭代更新,直至R({τi, αi}, {pu, i[n]}, {pd, j[n]})收敛,因此式(15)的算法描述如下:
步骤1 初始化{τn, αn}.随机产生一对{τn, αn},且满足τn+αn≤1;
步骤2 初始化{pu, i[n], pd, j[n]},根据式(18)、式(19)计算出{Ui, nopt},然后将{Ui, nopt}代入式(17),根据式(17)、式(20)计算出{Wi, nopt};
步骤3 将算出的{Ui, nopt}、{Wi, nopt}分别代入式(25)、式(26),计算{qu, i[n], qd, j[n]};
步骤4 判断R({qu, i}, {qd, j})是否达到收敛条件;否则,返回步骤2;
步骤5 固定计算出的{qu, i[n], qd, j[n]},使用内点法计算{τn, αn};
步骤6 判断R({τn, αn}, {qu, i}, {qd, j})是否达到收敛条件;否则,返回步骤.
3 仿真结果及分析针对干扰信道下的系统加权和速率进行了仿真分析.在上、下行信道中,信道增益为
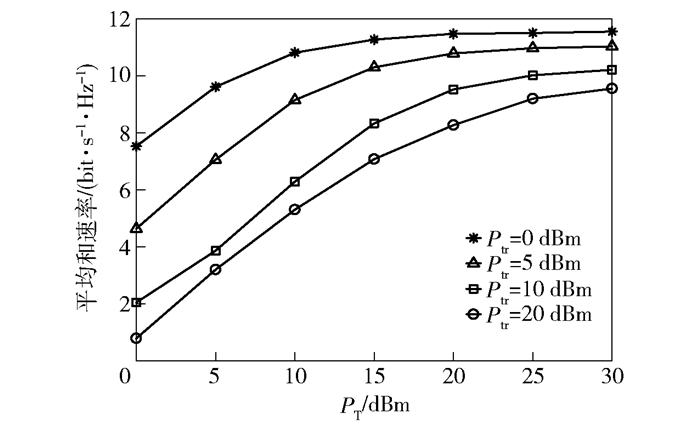
图 2所示为4个Ptr功率下,平均加权和速率随着基站功率PT增大的变化.从图 2可以看出,系统的平均加权和速率随着基站功率的增大而增大,但增大的趋势逐渐减缓.随着时间反演阶段探测信号功率的增大,系统的平均加权和速率逐渐减小,因为时间反演在聚焦信号的同时,也会对其他用户的上行传输产生干扰.
|
图 2 平均加权和速率与基站功率的关系 |
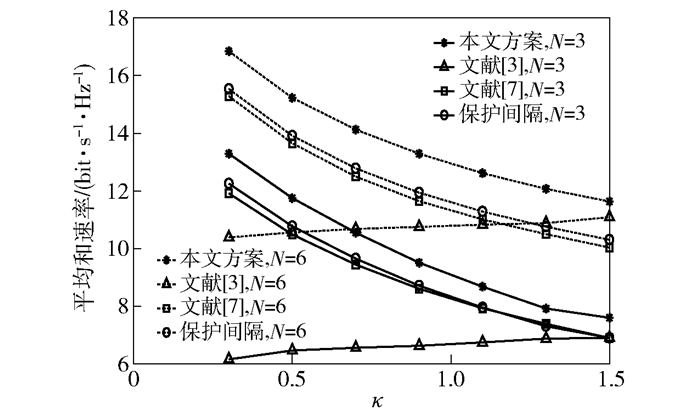
图 3所示为4种方案在不同信道干扰强度下的平均加权和速率.从图 3中可以看出,随着信道干扰强度的增加,所提方案、文献[7]方案及保护间隔方案中系统的平均加权和速率逐渐减小,但减小的趋势逐渐减缓,而文献[3]的TDMA方案中,随着信道干扰强度增加,系统的加权和速率增加,直至稳定.
|
图 3 干扰强度与平均加权和速率的关系 |
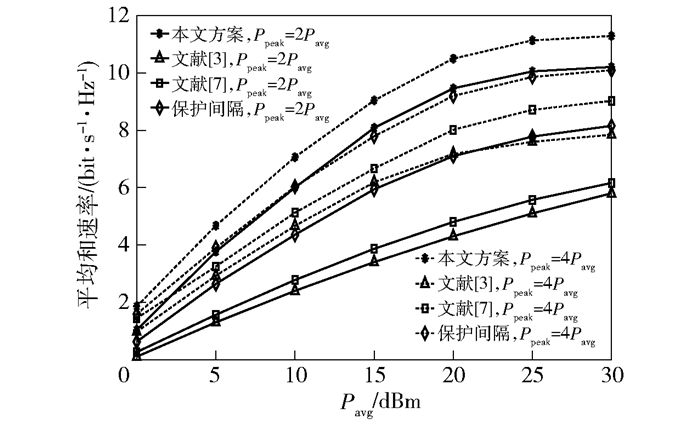
图 4所示为随着平均功率的增加,平均加权和速率的变化.从图 4可以看出,平均加权和速率随平均功率的增大而增大,并且在相同条件下,所提方案的平均加权和速率优于其他3种方案.
|
图 4 平均功率与平均加权和速率的关系 |
在干扰信道下,研究了多用户无线供电通信网络中的加权和速率最大问题.在引入时间反演技术抑制系统的交叉耦合干扰后,对多维时间段及上、下行传输功率进行分配,以求得系统的最大加权和速率,并分析了基站功率、信道干扰强度、平均功率等对平均加权和速率的影响.仿真结果证明了所提方案可以有效地抑制干扰,显著提升系统的平均加权和速率.
| [1] |
杨帆.无线供电的通信网络资源分配方法研究[D].北京: 北京邮电大学, 2019. http://cdmd.cnki.com.cn/Article/CDMD-10013-1019052748.htm
|
| [2] |
Choi K W, Ginting L, Rosyady P A, et al. Wireless-powered sensor networks:how to realize[J]. IEEE Transactions on Wireless Communications, 2016, 16(1): 221-234. |
| [3] |
Ju H, Zhang R. Throughput maximization in wireless powered communication networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(1): 418-428. DOI:10.1109/TWC.2013.112513.130760 |
| [4] |
Liu L, Zhang R, Chua K C. Multi-antenna wireless powered communication with energy beamforming[J]. IEEE Transactions on Communications, 2014, 62(12): 4349-4361. DOI:10.1109/TCOMM.2014.2370035 |
| [5] |
Lee H, Lee K J, Kong H B. Sum-rate maximization for multiuser MIMO wireless powered communication networks[J]. IEEE Trans Veh Technol, 2016, 65(11): 9420-9424. DOI:10.1109/TVT.2016.2515607 |
| [6] |
Kim W, Yoon W. Energy efficiency maximization for WPCN with distributed massive MIMO system[J]. Electronics Letters, 2016, 52(19): 1642-1644. DOI:10.1049/el.2016.2167 |
| [7] |
Kim H, Lee H, Duan Lingjie, et al. Sum-rate maximization methods for wirelessly powered communication networks in interference channels[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6464-6474. DOI:10.1109/TWC.2018.2859976 |
| [8] |
Rezaei O, Naghsh M M, Rezaei Z, et al. Throughput optimization for wireless powered interference channels[J]. IEEE Transactions on Wireless Communications, 2019, 18(5): 2464-2476. DOI:10.1109/TWC.2019.2901491 |
| [9] |
Shen Zukang, Khoryaev A, Eriksson E, et al. Dynamic uplink-downlink configuration and interference management in TD-LTE[J]. IEEE Commun Mag, 2012, 50(11): 51-59. DOI:10.1109/MCOM.2012.6353682 |
| [10] |
Shi Qingjiang, Razaviyayn M, Luo Zhiquan, et al. An iteratively weighted MMSE approach to distributed sum-utility maximization for a MIMO interfering broadcast channel[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4331-4340. DOI:10.1109/TSP.2011.2147784 |


