2. 湖南省铀尾矿库退役治理技术工程技术研究中心, 衡阳 421001
针对无线传感器网络中能耗不均衡问题,提出了一种基于改进萤火虫算法优化反向传播神经网络的非均匀分簇路由协议.通过在萤火虫算法中引进权重因子并增加4个评价指标,来平衡簇内负载和减少簇间的通信距离.结合BP神经网络,优化路径选择和簇首选举方式,达到最佳成簇效果.仿真结果表明,改进萤火虫算法优化BP神经网络的非均匀分簇路由协议能有效延长网络生命周期,节省能量,并均衡能耗.
2. Hunan Province Engineering Technology Research Center of Uranium Tailings Treatment Technology, Hengyang 421001, China
Aiming at solving the problem of uneven energy consumption in wireless sensor networks (WSNs), an uneven clustering routing protocol based on the improved firefly algorithm optimized back propagation(BP) neural network (IFABPUC) is proposed. To balance the intra-cluster load and reduce the inter-cluster communication distances, a weighting factor which takes into account four more evaluation indexes than the conventional firefly algorithm is embedded in the improved firefly algorithm. To achieve the best clustering, BP neural network is combined to optimize the way to path selection and cluster head election. Simulations show that IFABPUC can effectively extend the lifecycle of networks, save energy and balance energy consumption.
无线传感器网络(WSNs,wireless sensor networks)广泛应用于环境监测、生产生活等邻域[1].经典的低功耗自适应集簇分层型(LEACH,low-energy adaptive clustering hierarchy)[2]协议分为簇建立、稳态2个阶段,但其不能保证簇首数目、节点能量及节点位置的均匀分布.为此,提出了WSNs中的LEACH改进协议和分簇融合决策思想[3],验证了该协议对能耗以及时耗的优化效果,提升了融合准确率.高能效非均匀分簇协议(EECS,energy-efficient uneven clustering)[4]采取多跳路由使簇内节点能量与簇头能耗之间趋于平衡,但该协议易发生局部极值且未解决可靠性实时性问题.基于上述情况,采用临时簇首竞争半径构造非均匀分簇,并结合簇间多跳路由,优化网络节点的能耗[5-6];而当簇规模较大时,容易导致簇间信号传输不畅,通信链路断开.蚁群算法(ACO, ant colony optimization)通过改变周期性簇首选举方式也能使非均匀分簇路由得到优化[7],但是在更新速度以及路径质量的选择上有所不足.近年来,反向传播神经网络(BPNN, back propagation neural network)和萤火虫算法得到了快速发展,但存在着网络结构选择容易迟缓、收敛速度慢、局部极值以及泛化能力差等缺陷.
针对上述协议的不足,提出一种基于改进萤火虫算法优化BP神经网络的非均匀分簇路由协议(IFABPUC,uneven clustering routing protocol based on BP neural network optimization by improved firefly algorithm).利用改进萤火虫算法中荧光素浓度更新原则与局部簇首密度、簇首临近距离、簇首位置、节点距离等因子相结合,优化分簇,簇间采用代价函数构造转发树,形成距离基站两级梯度单、多跳传输,优化路径选择和簇首选举,并开展仿真及分析.
1 网络能量消耗模型假设WSNs具有如下性质:
1) 节点随机布置在监测区,ID唯一;
2) 节点和基站部署后位置均固定,节点能量无法补充,基站(sink节点)能量无限;
3) 感知类节点能力相似,地位平等;
4) 所有节点具有位置感知能力,依据接收信号强度判断彼此距离,并借此调整发射功率;
5) 采用数据融合技术减少数据传输量.
WSN节点数据传输能量衰减主要依据发送方和接收方的距离与临界值
| $ {E_{{{\rm{T}}_{\rm{X}}}}}(l,d) = \left\{ {\begin{array}{*{20}{l}} {l{E_{{\rm{elec}}}} + l{\varepsilon _{{\rm{fs}}}}{d^2}}\\ {l{E_{{\rm{elec}}}} + l{\varepsilon _{{\rm{mp}}}}{d^4}} \end{array},d < {d_{{\rm{init}}}}} \right. $ | (1) |
节点接收数据能耗ERx为
| $ {E_{{\rm{Rx}}}}(l) = l{E_{{\rm{elec}}}} $ | (2) |
其中:l为发送二进制位数,d为发送距离,Eelec为射频能耗系数,在自由空间和多径衰落区域中n分别取为2和4. εfs和εmp分别表示2种信道模型下功率放大电路能耗系数.
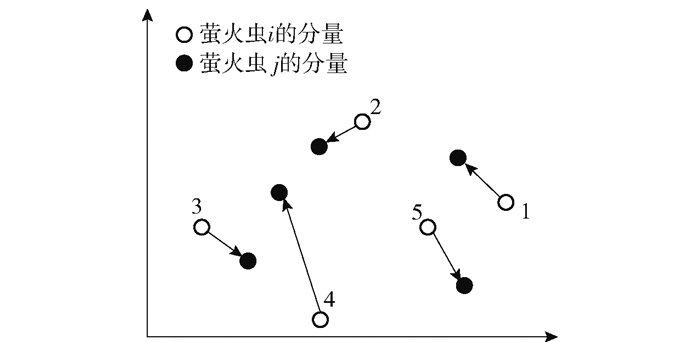
2 萤火虫算法 2.1 基本萤火虫算法萤火虫优化算法是一种模拟萤火虫发光特性并基于群体智能搜索的随机优化算法[9].该算法中,把空间分布的各点视为萤火虫个体.荧光素弱的萤火虫会被荧光素强的萤火虫吸引并向其移动,不断造成位置的更新迭代,完成寻优过程.搜索过程与萤火虫的发光亮度和相互吸引度2个重要参数有关,且都与距离成反比.发光越亮代表所处位置越好,亮度最大萤火虫即代表函数的最优解;发光亮度相同,则萤火虫做随机无规则运动.萤火虫初始位置在选取过程中也存在着随机性,从而使得两个分量间可能无法满足充分辨识度的对应关系,如图 1所示.
|
图 1 萤火虫分量的对应关系 |
FA算法具体优化机制如下所示.
荧光素相对值为
| $ {I_i}(t) = {I_0}{{\rm{e}}^{ - \gamma {r_{ij}}}} $ | (3) |
其中:I0为rij=0处对应最大萤光亮度;γ为光强吸收因子,取值为[0, 1]的常数,通常定义为常数1;rij为萤火虫i与萤火虫j之间的欧几里德距离.
邻域集合更新模型为
| $ {N_i}(t) = \left\| {{x_i}(t) - {x_j}(t)} \right\| = \sqrt {\sum\limits_{d = 1}^D {{{({x_{i,d}} - {x_{j,d}})}^2}} } $ | (4) |
其中:D为空间维数,xi, d与xj, d分别为在t时刻萤火虫xi与xj在空间中的第d个分量.
萤火虫i与萤火虫j之间的吸引度为
| $ {\beta _{ij}} = {\beta _0}{{\rm{e}}^{ - \gamma r_{ij}^2}} $ | (5) |
其中β0为rij=0处即最大吸引度.
萤火虫i被萤火虫j吸引的位置更新模型为
| $ \begin{array}{*{20}{l}} {x_i^{k + 1}(t + 1) = x_i^k(t) + {\beta _0}{e^{ - \gamma r_{ij}^2}}(x_j^k - x_i^k) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha (\varphi - 0.5)} \end{array} $ | (6) |
其中:k为当前迭代次数;xik为迭代到k代时第i只萤火虫对应的位置;α为步长因子,取值为[0, 1]的常数;φ为[0, 1]上的随机因子.
荧光素值更新模型为
| $ {I_i}(t + 1) = (1 - \delta ){I_i}(t) + \gamma f[{x_i}(t)] $ | (7) |
其中:δ为荧光素挥发因子,通常取[0, 1]的常数;f [xi(t)]为在t时刻,萤火虫i所对应的目标函数.
萤火虫个体决策范围更新模型为
| $ \begin{array}{*{20}{c}} {r_d^i(t + 1) = {\rm{min}}\{ {r_s},{\rm{max}}[0,r_d^i(t) + }\\ {\phi ({n_i} - |{N_i}(t)|)]\} } \end{array} $ | (8) |
其中:rdi(t)为在t时刻萤火虫i的决策半径,rs为决策范围,ni为萤火虫邻域阈值,ф为萤火虫邻域变化率.
2.2 改进萤火虫算法萤火虫算法具有一定的局限性.例如算法可能在极值点附近重复振荡,且在k有限的情况下φ存在无法跳出振荡的可能,而当萤火虫距离较远时,容易出现局部最优,也即降低了算法精度[10].为此,提出了一种改进萤火虫算法(IFA,improved firefly algorithm),通过引进权重因子ω(t)进行优化,优化后萤火虫位置更新模型为
| $ \begin{array}{l} x_i^{k + 1}(t + 1) = x_i^k(t) + \omega (t){\beta _0}{{\rm{e}}^{ - \gamma r_{ij}^2}}(x_{{\rm{best}}}^k - x_i^k) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha (\varphi - 0.5) \end{array} $ | (9) |
其中:ω(t)为随迭代次数变化的权重因子,通常取[0, 1]的常数;xbestk为迭代到k代时存在的最优萤火虫个体.
| $ \left. {\begin{array}{*{20}{l}} {{\lambda ^k}(t) = \frac{1}{n}\sum\limits_{i = 1}^m {\{ f[x_i^k(} t)] - f[x_{{\rm{ best }}}^k(t)]{\} ^2}}\\ {f[x_i^k(t)] = f[x_{i,1}^k(t),x_{i,2}^k(t), \cdots ,x_{i,m}^k(t)]}\\ {f[x_{{\rm{ best }}}^k(t)] = {\rm{min}}f[x_i^k(t)],i = 1,2, \cdots ,n} \end{array}} \right\} $ | (10) |
其中:λk(t)为权重因子变化的平滑程度;f[xik(t)]为在t时刻,第i个萤火虫在第k次更新后所对应的目标函数,k=1, 2, …, n;f [xbestk(t)]为在t时刻,第k次更新后最优萤火虫个体所对应的目标函数.
同时,为了平衡迭代时的收敛速度及精度,将步长因子α调整为
| $ \alpha = {\alpha _0}\frac{{\left\| {{x_i} - {x_{{\rm{ best }}}}} \right\|}}{{{l_{{\rm{ max }}}}}} $ | (11) |
其中:α0为初始步长因子,取值为[0, 1]的常数;‖xi-xbest‖为当前时刻第i个萤火虫与最优萤火虫之间的欧几里德距离;lmax为最优萤火虫与邻域萤火虫之间的最大距离.
为了确保算法的全局搜索能力,对超出部分的萤火虫位置调整为
| $ {x_i} = \left\{ {\begin{array}{*{20}{l}} {{x_{{\rm{max}}}},}&{{x_i} > {x_{{\rm{max}}}}}\\ {{x_{{\rm{min}}}},}&{{x_i} < {x_{{\rm{min}}}}} \end{array}} \right. $ | (12) |
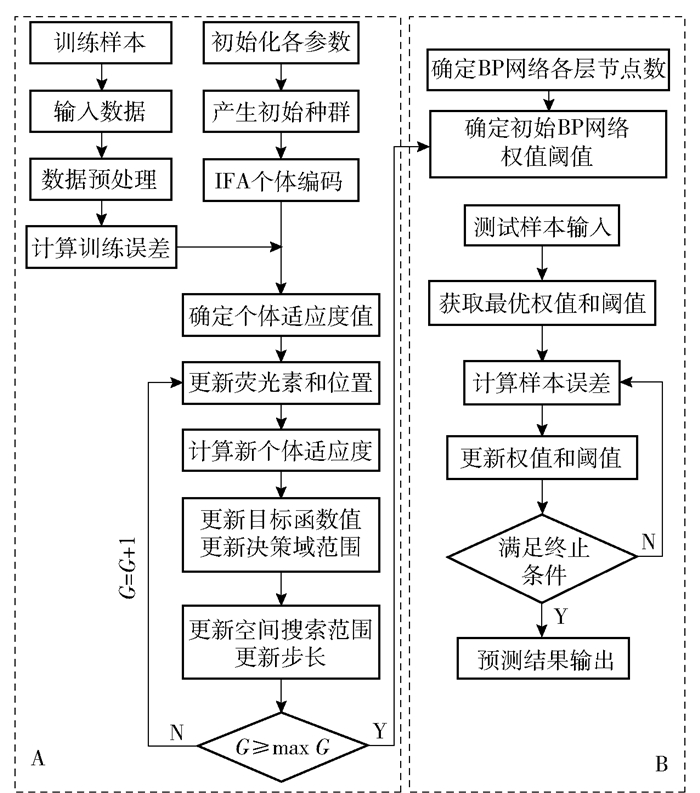
IFABPUC算法流程如图 2所示,该流程包括IFA算法实现(A部分)和BP神经网络实现(B部分)2部分,其中G为迭代次数,直至达到最大迭代次数,输出全局极值点和最优个体值. IFA算法实现步骤如下:
|
图 2 IFABPUC算法流程 |
1) 设置N、γ、β0、k、α等网络参数;
2) 计算萤火虫初始位置处的适应度值即对应的最大萤光亮度I0;
3) 更新荧光素及萤火虫位置,计算新个体的适应度值,进而更新目标函数值及决策域范围;
4) 对超出搜索范围的萤火虫以动态随机局部搜索进行约束,并更新步长;
5) 完成一次迭代过程后,判断是否满足终止条件,若是,则输出最优权重和阈值得到最优个体值;否则重新开始迭代.
BP神经网络具有初步的自组织、自适应能力,关键还展现出极强的非线性映射能力,对外界刺激、输入信息快速的联想记忆能力,对输入样本拥有很强的分辨能力以及优化计算能力. BP神经网络实现步骤如下:
1) 确定BP网络各层节点数、初始网络权值及阈值,对初始种群中的个体进行编码,并进一步在IFA算法中优化、执行;
2) 构造IFABP神经网络,通过训练样本计算系统网络的训练误差,并将其作为适应度值,满足终止条件时停止对系统网络的训练;
3) 通过测试样本开展对IFABP神经网络的检验,从而预测样本输出结果.
3.2 IFABPUC簇生成算法由于分簇算法的复杂性,在进行簇首选举时相关节点之间存在着大量的信息交换,这会给整个网络造成巨大能量开销.为此,综合考虑了簇首的局部密度、簇首临近距离、紧凑性、能量和位置等几方面的因素,提出了适应度函数.在选举簇首时,尽量将簇首予以分散,避免遗漏数据信息,使近距离节点快速加入簇首.介于簇首能耗远大于其他成员节点,为避免簇首能量过早耗尽而死亡,需对簇首能量进行评价.簇首始终由能量最高的节点担任,可有效均衡簇首能耗.簇首为网络中的关键节点,因此要对簇首位置进行规划,尽量减小距离汇聚节点近的簇首规模,以便实现多个簇首承担数据转发任务,提高数据实时性,减少簇首能耗.簇首更新时间为每轮迭代开始时.
假设在某一WSNs中具有N个节点,形成K个簇,候选簇首为M(节点能力相似,都可以担当簇首或簇内节点,则有K≪M),则网络有CNK种分簇方法,在其中选择最优分簇方法则是一个优化问题.利用IFA中适应度函数求解最优分簇方法,同时合理控制簇头因分散性而产生的非均匀网络分簇.
根据网络节点的能量信息,基站计算所有节点平均能量.剩余能量比平均能量大的节点作为本轮的候选簇首.然后,基站运行IFABPUC算法确定最优分簇方法(最大适应值),适应度函数公式为
| $ F = \sum {{\varepsilon _i}} {h_i}({P_j}),i = 1,2,3,4 $ | (13) |
其中:h1为簇首临近距离评价因子,临近距离越大即簇首与局部密度ρi大的簇首越分散,通过限定簇首临近距离能够保证簇首的分散性;h2为簇首紧凑性评价因子,即节点到对应簇首的最小平均距离;h3为簇首能量评价因子,即簇首能量之和与网络所有节点能量之和的比值;h4为簇首位置评价因子;εi为各因子对应的权重系数,∑εi=1.
簇首局部密度ρi通过核函数形式构造为
| $ {\rho _i} = \sum\limits_{j \in {I_S}} {{{\rm{e}}^{ - {{\left( {\frac{{{d_{ij}}}}{{{d_c}}}} \right)}^2}}}} ,S = \{ {a_i}\} _{i - 1}^K $ | (14) |
其中:dij为簇首i到簇首j之间的欧几里德距离,dc为断面距离,S为簇首集合.
h1表达公式为
| $ {h_1} = \left\{ {\begin{array}{*{20}{l}} {\mathop {{\rm{min}}}\limits_{j \in I_S^i} \{ {d_{ij}}\} ,}&{I_S^i \ne \varnothing }\\ {\mathop {{\rm{max}}}\limits_{j \in I_l^i} \{ {d_{ij}}\} ,}&{I_S^i = \varnothing } \end{array}} \right. $ | (15) |
| $ I_S^i = \{ K \in {I_s}:{f_K} > {f_i}\} $ | (16) |
h2表达公式为
| $ {h_2} = 1/\mathop {{\rm{max}}}\limits_{K = 1,2, \cdots ,K} \left\{ {\sum\limits_{\forall \in {C_{{P_j},K}}} {\frac{{d({n_i},{H_{{P_j},K}})}}{{|{C_{{P_j},K}}|}}} } \right\} $ | (17) |
其中:d(ni, HPj, K)为节点ni与相对应簇首之间的欧几里德距离,|CPj, K|为簇CK的节点数目.
h3表达公式为
| $ {h_3} = \frac{{\sum\limits_{K = 1}^K E ({H_{{P_j},K}})}}{{\sum\limits_{i = 1}^N E ({n_i})}} $ | (18) |
h4表达公式为
| $ {h_4} = \frac{{Kd({B_{\rm{S}}},{W_{\rm n}})}}{{\sum\limits_{i = 1}^K d ({B_{\rm{S}}},{H_{{P_j},K}})}} $ | (19) |
其中:BS为基站,Wn为网络中心.
依据适应度函数的设计,最大适应度函数值可同时满足簇首分散性较好、簇几何结构紧凑、簇首能量之和较大、簇首离基站较近的条件.根据适应度函数形成的网络分簇能获得较小簇内能耗,并在基站较近的地方形成较多分散的簇首和规模较小的簇,有效地平衡簇间能耗.
初始化P个萤火虫,每个萤火虫表示一种分簇方式,并包含K个候选簇头.计算节点ni和所有簇首Hi, K的距离d(ni, Hi, K),将节点ni分配至最近簇首,这也就平衡了簇内负载,减少了通信距离.
3.3 IFABPUC簇间转发树簇间是以通信能耗和相临簇首的剩余能量作为代价函数的参考依据,选通信距离较短且剩余能量较大的节点作为下一跳,构建簇间转发树.从能耗模型可知,能耗与传输距离成指数关系,如果簇首采用单跳传输方式,将产生大量能耗.在簇首之间构建生成树,数据以多跳方式传输到汇聚节点,可有效减少能耗.生成树的构成需要所有簇首收集邻居簇首的信息,在簇生成结束之后,簇首以通信半径的2倍(2r)广播公告消息TREE_ADV_MSG (ID, En, d_Qsink),消息中含有簇首ID、剩余能量En和簇首到汇聚节点Qsink的距离d;此外节点接收TREE_ADV_MSG信息时,依据接收信号强度计算相临簇首与其的距离.在簇头接收簇成员发送的JOIN_REQ_MSG(ID)后,进而广播SCHED_MSG并由成员接收.根据簇首接收的信息,簇首选择合适的临簇首作为下一跳.对于簇首节点i而言,假设临簇首的集合为Si,则下一跳的Pi选择条件如式(20)~式(22)所示.
| $ {P^i} = \left\{ {\begin{array}{*{20}{l}} {{Q_{{\rm{ sink }}}},\quad d(i,{Q_{{\rm{ sink }}}}) < 2r}\\ {j,\quad {\rm{ 其他 }}} \end{array}} \right. $ | (20) |
| $ \begin{array}{*{20}{c}} {j = {\rm{argmin}} \{ {\rm{cost}} (k),\forall k \in {S^i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}}\\ {d(k,{Q_{{\rm{ sink }}}}) < d(i,{Q_{{\rm{ sink }}}})\} } \end{array} $ | (21) |
| $ {\rm{ cost}} (k) = \tau \frac{{{d^2}(i,k) + {d^2}(k,{Q_{{\rm{ sink }}}})}}{{{d^2}(i,{Q_{{\rm{ sink }}}})}} + (1 - \tau )\frac{{{{\bar E}_n}(i)}}{{{E_c}(k)}} $ | (22) |
其中:d为簇的距离;r为Qsink的通讯半径;cost(k)为代价函数;τ为权重系数,取值为[0, 1]的常数.
当簇首节点与基站之间的距离小于通讯范围2r时,簇首直接将数据传输给基站; 否则,簇首将选择一个代价函数最小且距离基站较近的临簇首作为下一跳节点.
4 模型仿真与验证 4.1 消息复杂度WSNs中存在N个网络节点,运行前基站向全网广播请求REQMSG(ID, xBS, yBS),内容包含自身位置及ID,之后收到该请求的每个网络节点则相应的发出包含自身位置、ID、初始能量的响应SELF_INTO_MSG(ID, x, y, E0),其中E0为节点初始能量.候选簇首由N×T个网络节点参与消息竞争,竞争过程共广播N×T条COMPETE_CH_START_MSG消息,邻居节点收到消息退出竞争.假设K个候选簇首竞选成功,广播K条FINAL_CH_MSG消息和K条CH_ADV_MSG消息,其余节点广播N-K条JOIN_CLUSTER_MSG消息.综上所述,该阶段网络中总开销为
| $ NT + K + K + N - K = K + N(1 + T) $ | (23) |
EEUC消息复杂度为N(1+2T),则IFABPUC的总开销比EEUC小(TN-K).
4.2 仿真参数设置利用Matlab对LEACH、EEUC和IFABPUC协议在相同参数条件下进行仿真,比对三者中存活节点数、剩余能量均值、方差、数据传输时延、单轮平均消息数及簇首变化情况.仿真参数设置如表 1所示.
|
|
表 1 主要参数设置 |
|
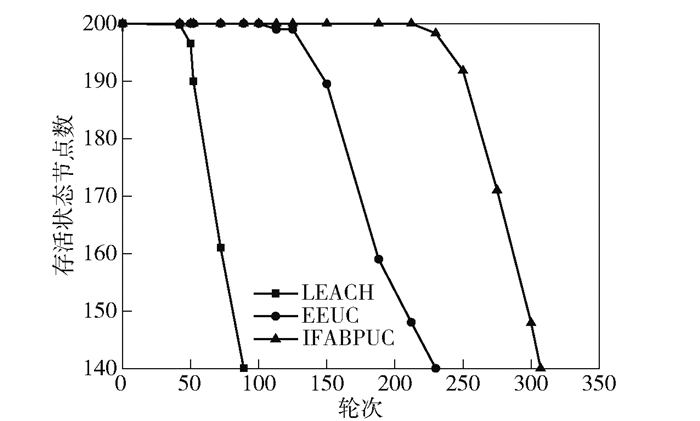
图 3 网络生命周期对比 |

|
图 4 网络剩余能量均值对比 |
|
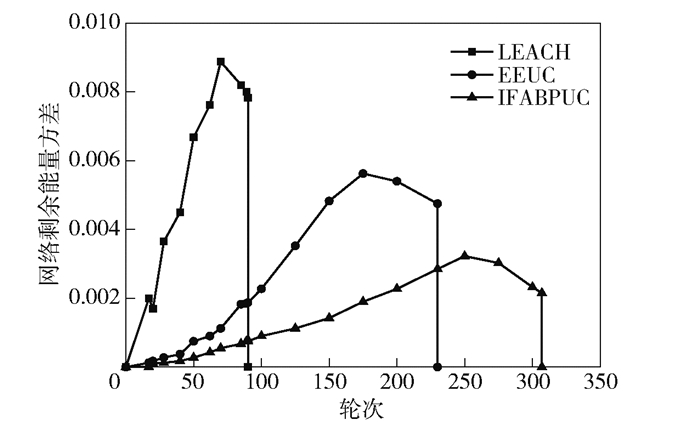
图 5 网络剩余能量方差对比 |
|
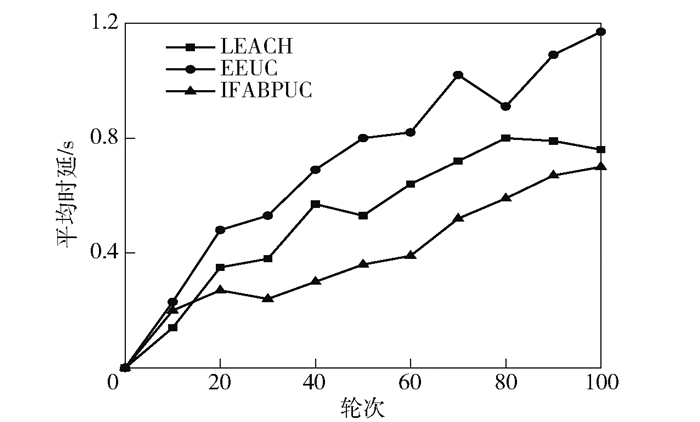
图 6 数据传输平均时延对比 |

|
图 7 不同规模网络单轮平均消息数对比 |
|
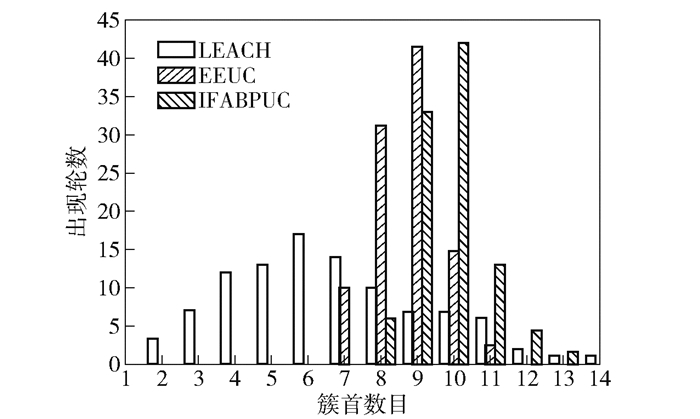
图 8 簇首数目变化统计 |
网络生命周期对比如图 3所示.图中LEACH、EEUC和IFABPUC三种协议的首个死亡节点分别出现在第37轮、第113轮和第215轮.此处将死亡节点数超过节点总数30%的时间定义为整个系统网络有效死亡时间te,则上述3种协议te分别出现在第89轮、第234轮和第307轮,IFABPUC协议相对于LEACH协议和EEUC协议,网络生命周期分别延长244.9%和31.2%.这是由于IFABPUC采用优化后的局部候选簇首竞争方法,控制了簇首节点数目及簇规模,避免了随机选举能耗过大的缺陷,具有良好的稳定性和可靠性,从而缓解了节点数据传输压力,均衡了整体能耗.
图 4和图 5所示为网络节点剩余能量均值和节点剩余能量方差对比. IFABPUC的节点剩余能量均值一直高于LEACH和EEUC,明显处于优势,表明IFABPUC能够有效节省能量. 图 5显示IFABPUC的网络节点剩余能量方差低于LEACH和EEUC,并处于相对平稳的状态.由于IFABPUC利用适应度函数优化后,使网络拥有了更长的存活时间,表明IFABPUC协议可以更有效地实现网络节点能量均衡,进而实现更优异的网络监控性能.
图 6中,LEACH协议的平均时延小于EEUC协议,IFABPUC协议的数据传输平均时延最小,特别是20轮后的效果更佳.通过优化网络路径选择及簇首选举方式,可使簇头与簇内节点之间的通信更加畅通,保证了网络中传感器节点数据发送的公平性,表明IFABPUC网络整体稳定性最好.
图 7所示为不同规模网络单轮平均消息数对比,当轮数少于120时,IFABPUC的平均消息数与EEUC之间的差距并不大,之后的表现也比较平稳,数据信息的传输效益较高,消息复杂度变化并不明显.
当网络拓扑结构固定时,稳定的分簇路由算法会产生相对一致的簇头数,以此优化网络的能耗. 图 8所示为3种协议在随机选取的100轮中簇首节点数目统计情况.图中,LEACH簇首数目较小,波动范围较大,这是因为其只通过随机数及阈值机制来选举簇首;EEUC生成的簇首数目相对于LEACH更稳定、集中,但IFABPUC生成的簇首数目较EEUC明显更多一点,这是因为IFABPUC通过适应度函数确定最优分簇方法(最大适应值),使得近基站生成比较分散的簇头,簇首数目较多,簇规模小,产生簇内能耗更少,可更有效地转发数据.
综上所述,LEACH采用主路径传输数据,会导致主路径中节点的能耗加剧,而通过周期性等概率随机选举产生的簇头所构建出的规模相同的簇所达成的局部能耗会优先消耗掉远基站簇头能量,且造成簇首数目波动明显. EEUC通过采用局部候选簇首竞争的方法,使得近基站簇规模较小,数据传输过程消耗的能量较低,缓解了能耗不均衡.而IFABPUC通过适应度函数形成的网络非均匀分簇产生了更稳定的簇首数目.更分散的簇首节点以及更合适的簇群规模,在簇内实现了较小的能量消耗,有效增强了网络的可靠性和稳定性,并大幅延长了网络的生命周期,节省了能量,实现了网络节点能量的均衡.
5 结束语根据现实路由网络的需要,针对WSNs能耗不均衡的问题,提出了IFABPUC路由协议.通过在IFA和BPNN理论中引入网络簇首影响因子,构成非均匀簇,优化路径选择实现簇首能耗均衡.通过对网络生命周期、网络剩余能量、数据传输时延、簇首变化情况等几方面进行仿真,结果表明,IFABPUC路由协议与LEACH、EEUC协议相比能更好地实现能耗均衡,保持网络的可靠性和稳定性,同时也能更有效地节省节点能量,并在一定程度上提升网络生存周期.
| [1] |
胡长俊, 袁树杰. 矿井WSN自适应能量有效及能耗均衡的数据收集方法[J]. 北京邮电大学学报, 2018, 41(2): 86-91. Hu Changjun, Yuan Shujie. An adaptive data collection method of energy efficiency and energy consumption balance in WSN for coal mines[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(2): 86-91. |
| [2] |
Singh S K, Kumar P, Singh J P. A survey on successors of LEACH protocol[J]. IEEE Access, 2017, 5(99): 4298-4328. |
| [3] |
黄利晓, 王晖, 袁利永, 等. 基于能量均衡高效WSN的LEACH协议改进算法[J]. 通信学报, 2017, 38(S2): 164-169. Huang Lixiao, Wang Hui, Yuan Liyong, et al. Improved LEACH protocol algorithm for WSN based on energy balance and high efficiency[J]. Journal on Communications, 2017, 38(S2): 164-169. |
| [4] |
Chen Guihai, Li Chengfa, Ye Mao, et al. EECS:an energy efficient clustering scheme in wireless sensor networks[J]. Journal of Frontiers of Computer Science & Technology, 2007, 3(2-3): 99-119. |
| [5] |
刘伟, 杜佳鸿, 贾素玲, 等. 能量有效的无线传感器网络分簇路由协议[J]. 北京航空航天大学学报, 2019, 45(1): 50-56. Liu Wei, Du Jiahong, Jia Suling, et al. Energy efficient clustering routing protocol for wireless sensor networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(1): 50-56. |
| [6] |
Dutta R, Gupta S, Das M K. Low-energy adaptive unequal clustering algorithm using fuzzy c-means in wireless sensor networks[J]. Wireless Personal Communications, 2014, 79(2): 1187-1209. DOI:10.1007/s11277-014-1924-7 |
| [7] |
刘宏, 李好威. 基于蚁群优化的非均匀分簇路由算法[J]. 华中科技大学学报(自然科学版), 2018, 46(8): 50-54. Liu Hong, Li Haowei. Uneven clustering routing algorithm based on ant colony optimization[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(8): 50-54. |
| [8] |
Heinzelman W B, Chandrakasan A P, Balakrishnan H. An application-specific protocol architecture for wireless microsensor networks[J]. IEEE Transactions on Wireless Communications, 2002, 1(4): 660-670. DOI:10.1109/TWC.2002.804190 |
| [9] |
Shindo T, Xiao J, Kurihara T, et al. Analysis of the dynamic characteristics of firefly algorithm[C]//2015 IEEE Congress on Evolutionary Computation (CEC 2015). Sendai: IEEE, 2015: 2647-2652. https://www.researchgate.net/publication/322062141_Analysis-of-the-Dynamical-Characteristics-of-the-Firefly-Algorithm
|
| [10] |
Wang Yong, Cai Zixing, Zhou Yuren, et al. Constrained optimization based on hybrid evolutionary algorithm and adaptive constraint-handling technique[J]. Structural and Multidisciplinary Optimization, 2009, 37(4): 395-413. |


