2. 北京邮电大学 灾备技术国家工程实验室, 北京 100876
互联网的发展导致各种信息传输量的激增,对于大数据的处理,奈奎斯特采样定律已经不能满足许多实际工程应用的需要,而压缩感知的出现解决了这个问题.压缩感知理论指出稀疏信号可以用远小于奈奎斯特采样定律的采样数进行采样,并将原始数据恢复出来.压缩感知不仅可以将数据进行压缩,而且还具有加密功能,被广泛应用到信息和网络的安全理论中.为了实现更好的加密效果,对压缩感知与其他多种技术相结合(如混沌系统、置乱和扩散等)的安全方案进行汇总,并对现有的多种方案的对比结果进行了对比分析.结果表明,现有的这些压缩感知安全方案都可以达到良好的加密效果,可以抵抗暴力攻击、统计攻击、已知明文攻击等多种攻击,具有良好的安全性.
2. National Engineering Laboratory for Disaster Backup and Recovery, Beijing University of Posts and Telecommunications, Beijing 100876, China
The rapid development of Internet induces huge requirement on transmission, which calls for much more efficient techniques to compress information. Compressive sensing method can sample sparse signals with much less samples than Nyquist's sampling law with payload of recovery quality and computation complexity. Compressive sensing can not only compress data, but also encrypt them, and thus can be applied to encrypt the information and network. The article reviews the compressive sensing-based encryption methods, which combines other technologies (such as chaotic system, scrambling and diffusion). After analyzing the performance comparison of existing methods, the compressive sensing-based schemes is verified to achieve a great security capability to resist brute-force attack, statistical attack, known plaintext attack and other attacks.
信息传输量的增大,传输速度的要求增加,需要更有效地压缩采样方法来实现更高的采样速率和信号处理速度,压缩感知的出现使这个问题得以解决. 2006年,Candes[1]、Romberg[1]、Taos[1]和Donoho[2]正式提出了压缩感知(CS, compressive sensing)理论,并被广泛应用到无线传感网络、图像加密、图像数据隐藏、医疗监控等方面.
使用CS进行加密,则需要存储整个测量矩阵,需要很大的存储空间.然而,利用混沌系统则只需存储矩阵的生成参数,减少了存储空间,而且利用混沌系统对初始值和控制参数的敏感性可以实现“一次一密”的效果,所以研究人员将混沌系统和CS结合起来,设计了许多基于混沌压缩感知(CCS, chaos-based compressed sensing)的加密算法[3-5].混沌映射可以分为一维和高维混沌映射两类.由于一维映射结构简单,可以使用混沌信号估计技术预测其混沌值,从而容易受到安全威胁,因此一些高维的混沌映射或耦合的混沌系统被使用在加密方案中[6-8].
由于CS是线性操作的过程,易受选择明文攻击和已知明文攻击,将置乱和扩散技术与CCS进行结合,则可以打破线性操作,使之能够抵抗这2种攻击.常用的置乱和扩散技术有Arnold干扰[9]、3D cat map[10]、Zigzag混淆[11]和细胞自动机[12]等.置乱和扩散技术的作用是通过改变像素的位置,使原始数据看起来杂乱无章,从而达到加密的效果.
笔者首先对CS安全理论方案进行总结,分析其所用的方法和改进思路;其次对所提到的CS安全方案进行对比和评估,证明这些方案有良好的安全性能;最后进行总结及展望.
1 CS安全理论方案下面对经典CS方案的改进方案进行描述,使CS可以实现更好的加密效果.
1.1 基于CS的安全网络编码方案Xie等[13]提出了基于CS的安全网络编码方案,不仅解决了网络编码易受污染攻击的问题,同时可以保护传输数据的隐私.
该方案构建一种有效且简单的密钥分发中心,并使用Logistic映射来生成密钥,可信第三方可以通过安全通信信道将密钥分发给网络中的所有节点,且只需产生2个密钥:一个通过安全通道发送给源节点和宿节点,用来产生混沌映射构造测量矩阵;另一个秘密传送给源节点生成秘密向量.
基于CS的安全网络编码方案是利用混沌系统的敏感性来实现更好的加密效果的,可以抵抗污染攻击、标签攻击,且保护数据隐私.但该方案只使用一个测量矩阵来加密数据,而下面则使用2个混沌测量矩阵进行加密,提高了加密性能和安全性.
1.2 基于CCS的无线体域网安全节能数据传输方案无线体域网如今面临2个问题:节能和安全. Peng等[5]提出基于CCS的无线体域网安全节能数据传输系统,在解决节能问题的同时解决数据安全问题.
Peng等[5]使用混沌系统,只需存储矩阵生成参数,节省了存储空间,解决了无线体域网中的节能问题,并且使用Chebyshev映射、Logistic映射、Tent映射中的任意一个混沌映射生成2个混沌矩阵进行加密,增加了安全性,解决了无线体域网中的安全问题.
该方案使用混沌系统只需存储测量矩阵的生成参数,且利用混沌系统的敏感性,可以实现更好的加密效果.但该方案只是在地面上降低无线传感器采样的耗能,并没有将无线传感器的安全应用领域从地面扩展到水下.下面提出水下无线传感器网络的安全节能方案.
1.3 基于CCS的水下无线传感器网络安全节能传输方案CS一直被用于降低无线传感网络采样的耗能,但由于水下环境存在有限带宽、时变多径传播和高延迟的复杂性,它尚未被用在水下无线传感网络.
Li等[14]提出基于CCS的水下无线传感器网络节能安全传输方案.该方案首先用CS进行压缩采样数据,然后用CCS进行加密,此阶段利用了传感器的ID,根据传感器的ID生成混沌参数和初始值,通过Logistic映射来生成测量矩阵进行加密.该方案可确保测量矩阵与每个传感器的ID相关联,使不同的传感器有不同的测量矩阵.使用不同的测量矩阵来加密每个传感器的数据,避免了通过解密其中一个测量矩阵来窃取所有传感器的加密数据的风险.
该方案将无线体域网的安全领域应用扩展到了水下,并利用传感器的ID来确保测量矩阵与传感器相关联,使不同的传感器有不同的测量矩阵,增强了系统的安全性.但该方案只使用了传统的一维混沌映射,此混沌系统的混沌范围较小.下面将一维混沌映射进行结合,形成一个新的一维混沌映射,增加了混沌系统的混沌范围.
1.4 基于新的一维混沌映射与CS结合的压缩加密技术Ponuma等[6]提出了新的一维混沌映射与CS结合的压缩加密技术.结合Logistic、Sine、Tent映射形成的Logistic-Sine-Tent(STL)一维混沌映射,其混沌效果比传统的一维混沌映射效果好. STL是在3个一维混沌映射上执行融合和级联操作.首先将Logistic和Tent映射进行异或来进行融合操作,来动态生成新的混沌映射,然后将生成的新映射与Sine映射进行串联完成级联操作.根据输入的原始图像用SHA-256函数来获得密钥,进而得到混沌参数,生成混沌序列,来构造测量矩阵.使用SHA-256函数使得不同的数据有不同的密钥.干扰时,首先用Arnold干扰进行块干扰,然后根据混沌序列生成的索引序列来进行行干扰和列干扰,最后用混沌系统生成的整数序列与列干扰后进行光栅化后的序列进行异或来生成密码图像.该方案使用耦合的一维混沌系统,扩大了混沌系统的参数空间,提高了混沌性能.但该方案使用的混沌系统仍是一维的,参数和变量仍较少.使用超混沌系统,将混沌系统从二维空间扩展到三维空间.
1.5 基于超混沌、CS和循环移位的压缩加密方案Zhu等[7]将超混沌和CS进行结合,并用循环移位的方法进行再次加密.该过程包含2个阶段,第1阶段是CS阶段,第2阶段是循环移位和扩散操作阶段.在第1阶段中,Chebyshev映射用于生成服从高斯分布的测量矩阵,使用Sigmoid函数将压缩后的加密图像的测量值范围调整到0~255中.在第2阶段中,用超混沌映射生成4个混沌序列来进行干扰和扩散.
该方案通过使用CS可以迅速有效地发送和存储数据,超混沌、循环移位和扩散操作进一步增强了系统的安全性.但该方案使用的超混沌的参数空间仍不够大,且超混沌系统用在了干扰阶段,并未用于测量矩阵的生成.下面将磁控忆阻混沌系统与CS进行结合,将磁控忆阻混沌系统用于测量矩阵的生成,扩大了混沌系统的混沌范围.
1.6 基于磁控忆阻混沌系统和CS的图像加密方法Chai等[8]提出基于磁控忆阻混沌系统和CS结合的图像加密方法,此方案使用磁控忆阻混沌系统、SHA-512和细胞自动机等技术.
为了减少原始图像与加密图像的相关性,采用SHA-512来计算混沌系统的初始值,和1.4节中使用SHA-256达到了相同的效果,均使得在加密不同的数据时所使用的测量矩阵是不同的.该方案可以提高原始图像与算法的相关性,可抵抗已知明文攻击和选择明文攻击.
该方案使用的磁控忆阻混沌系统,将混沌范围大大扩大,并且使用细胞自动机等技术来进一步加强安全性.但该方案中及1.1~1.5节中所使用的测量矩阵必须满足矩阵相乘维数匹配条件,即传感矩阵的列数必须等于信号的长度,这样就对测量矩阵进行了限制.因此,引入半张量积CS(STP-CS, semi-tensor compressive sensing)来解决这个问题.
1.7 基于STP-CS的无线体域网安全数据传输方案Li等[9]提出将STP-CS应用在安全数据传输系统,使用混沌、半张量积、Arnold干扰、混沌干扰、SHA-256等技术,此方案是对1.2节的改进.
首先输入原始图像,根据原始图像计算SHA-256值.与1.4节中使用SHA-256来计算混沌参数的初始值不同,该方案使用SHA-256函数计算Arnold干扰数和干扰参数,并对稀疏图像进行Arnold干扰.然后用Logistic映射和Tent映射生成2个测量矩阵进行半张量积压缩,得到压缩图像.使用半张量积可以用同一测量矩阵压缩不同长度的信号,也可以使用更小的测量矩阵压缩同一信号.最后用混沌系统生成的混沌序列对压缩图像进行混沌干扰得到密码图像.
该方案使用了半张量积技术,可以使用更小的测量矩阵压缩同一信号,大大减少了存储空间.但该方案及1.1~1.6节的加密是在整个数据中进行的,从而处理速度相对较慢.为了提高CS的处理速度,下面提出基于并行压缩感知(PCS, parallel compressive sensing)的图像加密方案.
1.8 基于PCS的可视化安全图像加密方案Wang等[10]利用PCS计数器模式和嵌入技术设计了一种可视化安全加密方案.为了实现更高的安全级别,此方案引入Logistic-Tent混沌系统和3D cat map来构建测量矩阵,并使用Zigzag混淆进行干扰.
该方案使用并行技术,大大提高了加密速度,并且使用Zigzag混淆、3D cat map等技术来提高加密效果,做到了在提高加密速度的同时也提高了安全性.但该方案加密每列所使用的测量矩阵是相同的测量矩阵,且对于数据量非常大的信号或图像来说,经过一轮压缩后,数据还是非常大的,传输速度和处理速度仍比较慢,并且对传输带宽和存储空间也有限制.
表 1列出了以上所描述的CS安全理论研究方案的对比结果.
|
|
表 1 CS安全理论研究方案对比 |
下面对第1节中所提到的方案进行性能对比分析,分别选取文献[5]中的“Lena”、文献[6]中的“Baboom”、文献[7]中的“Rice”、文献[8]中的“Finger”、文献[10]中的“Brain”以及文献[9]中的512×512的“Lena”作为原始测试图像,测量矩阵维数为128×256.
2.1 加密和解密结果以文献[6]中的“Baboom”作为原始图像给出加密和解密结果. 图 1所示为加密和恢复结果.从图 1中可以看出,对加密图像进行了压缩,且无法从中识别出有关原始图像的信息.

|
图 1 文献[6]的加密和恢复结果 |
下面分别从直方图、相关性、信息熵来对所提出的CS安全理论方案进行统计分析.
1) 直方图分析
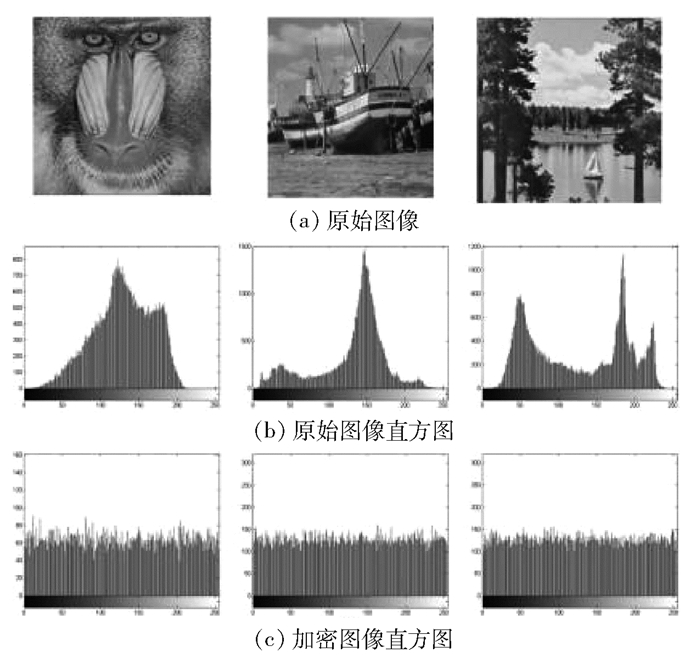
直方图可以直观地看出原始图像与加密图像的像素分布状态.原始图像的直方图是唯一的,易遭受统计攻击,为了阻止这种攻击,加密图像的直方图必须相对均匀且与原始图像的直方图不同.
以文献[6]中的“Baboom”、“Boat”、“Lake”分别作为原始图像. 图 2为原始图像的直方图和加密图像的直方图.从图 2中可以看出,加密图像的直方图相对均匀,且与原始图像的直方图不同.
|
图 2 文献[6]的原始图像和加密图像的直方图 |
2) 相关性分析
相关性分析是指对2个或多个具备相关性的变量元素进行分析,从而衡量2个变量因素的相关密切程度.对于加密图像来说,相邻像素相关性理论上应该趋近于0.
表 2给出了文献[5-7]、文献[9-10]中原始图像和加密图像在水平、垂直、对角方向上的相关系数.从表 2中可以看出,这些文献所述的加密图像在各方向上的相关系数均接近0,表明这些文献所述的安全方案加密效果好.
3) 信息熵分析
信息熵用来测量图像的灰度分布,信息熵越大,则灰度分布越一致.对于256×256的灰度图像,有效的加密系统加密后的图像的信息熵应接近理论值8.
表 3显示了文献[5-7]、文献[9-10]中原始图像和加密图像的信息熵.从表 3中可以看出这些文献中的加密图像的信息熵接近8,表明这些文献中给出的加密方案性能优越.
2.3 差分攻击差分攻击的思想是对原始测试图像进行细微的修改,并使用相同的加密算法分别加密原始图像和修改后的图像,找出这2个原始图像和对应的加密图像之间的联系.
测试原始图像的改变用像素变化率(NPCR,number of pixels change rate)和统一平均变化强度(UACI,unified averaged changed intensity).对于256× 256的灰度图像来说,它的加密图像的NPCR和UACI值要分别接近理论值99.61%,33.46%.
从表 4可以看出,文献[6-8]中的加密方案的NPCR均比较接近理论值99.61%,文献[6-7]中的加密方案的UACI均比较接近理论值33.46%.
2.4 密钥空间分析在密码学中,密钥空间是衡量加密算法的一个重要属性.密钥空间要够大,才能抵抗暴力攻击.通常情况下,密钥空间应大于2100.
表 5列出了文献[6-10]中的密钥空间大小,这些文献中给出的方案的密钥空间均足够大,可以抵抗暴力攻击.
2.5 密钥敏感度分析一个好的加密算法应该有良好的密钥敏感度,即发生一点小的改变,密钥就会发生改变,就会生成不同的密文,增大了攻击者的攻击难度.
第1节中提到的方案均使用了混沌系统,以文献[5]中的Chebyshev映射为例,来分析混沌系统的敏感性. Chebyshev映射可表示为
| $ z_{k+1}=\cos(ω\arccos \;z_{k}) $ | (1) |
其中:ω>2,zk∈[-1, 1]. z(k)混沌序列的初始值为0.32,z1(k)序列的初始值为0.320 000 000 000 01,2个混沌序列的混沌参数均为20,混沌序列长度均为256,d(k)为2个序列之间的差值. z(k)和z1(k)的初始值相差0.000 000 000 000 01,在k < 10时,2个序列几乎没有差别,但当k>10时,2个序列有很大的不同.从而可以看出混沌系统的灵敏度很高,适合加密.
2.6 选择明文攻击和已知明文攻击由于CS是线性操作,缺乏扩散机制,所以易遭受选择明文攻击和已知明文攻击.因此,可以通过扩散CS测量的线性度来阻止选择明文攻击和已知明文攻击.
第1节中提到的方案均在一定程度上使用扩散机制来破坏CS的线性操作.如Zhu等[7]使用循环移位、Li等[9]使用Arnold干扰和混沌干扰. Chai等[8]使用SHA函数和Li等[14]将传感器的ID和混沌系统相关联来生成混沌参数,均可以根据不同的原始数据来生成不同的测量矩阵进行加密. Wang等[10]对数据中的每个列进行加密,加密每列所使用的测量矩阵可以不同,攻击者即使得到测量矩阵,也无法获得有用的信息.因此,文献[7-10]、文献[14]中的方案均能有效地抵抗选择明文攻击和已知明文攻击.
3 结束语对CS安全理论研究的常用方法进行了归纳和总结,对现有的多种方案的性能进行对比分析,表明了现有的多种方案具有良好的加密效果,能抵抗暴力攻击、统计攻击等多种攻击,从而说明现有的多种方案都有良好的安全性.
重构算法是CS理论研究的核心问题.现阶段尽管有多种重构算法及改进方案,但是仍然满足不了现代社会的发展要求.为此,对CS的重构算法进行深入研究,尽可能地降低图形重建的观测值、简化图像重构的算法是需要一直关注和深入研究的问题.本研究为继续深入研究CS安全理论提供了一定的参考和借鉴.
| [1] |
Candes E J, Romberg J, Tao T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [2] |
Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [3] |
Zhang Yushu, Zhou Jiantao, Chen Fei, et al. Embedding cryptographic features in compressive sensing[J]. Neurocomputing, 2016, 205: 472-480. DOI:10.1016/j.neucom.2016.04.053 |
| [4] |
Xiao Di, Deng Mimi, Zhu Xinyi. A reversible image authentication scheme based on compressive sensing[J]. Multimedia Tools and Applications, 2015, 74(18): 7729-7752. DOI:10.1007/s11042-014-2017-z |
| [5] |
Peng Haipeng, Tian Ye, Kurths J, et al. Secure and energy-efficient data transmission system based on chaotic compressive sensing in body-to-body networks[J]. IEEE Transactions on Biomedical Circuits and Systems, 2017, 11(3): 558-573. DOI:10.1109/TBCAS.2017.2665659 |
| [6] |
Ponuma R, Amutha R. Compressive sensing based image compression-encryption using novel 1D-chaotic map[J]. Multimedia Tools and Applications, 2018, 77(15): 19209-19234. DOI:10.1007/s11042-017-5378-2 |
| [7] |
Zhu Shuqin, Zhu Congxu. A new image compression-encryption scheme based on compressive sensing and cyclic shift[J]. Multimedia Tools and Applications, 2019, 78(15): 20855-20875. DOI:10.1007/s11042-019-7405-y |
| [8] |
Chai Xiuli, Zheng Xiaoyu, Gan Zhihua, et al. An image encryption algorithm based on chaotic system and compressive sensing[J]. Signal Processing, 2018, 148: 124-144. DOI:10.1016/j.sigpro.2018.02.007 |
| [9] |
Li Lixiang, Liu Lifei, Peng Haipeng, et al. Flexible and secure data transmission system based on semi-tensor compressive sensing in wireless body area networks[J]. IEEE Internet of Things Journal, 2019, 6(2): 3212-3227. DOI:10.1109/JIOT.2018.2881129 |
| [10] |
Wang Hui, Xiao Di, Li Min, et al. A visually secure image encryption scheme based on parallel compressive sensing[J]. Signal Processing, 2019, 155: 218-232. DOI:10.1016/j.sigpro.2018.10.001 |
| [11] |
Murillo E M A, Cruz H C, Abundiz P F, et al. A RGB image encryption algorithm based on total plain image characteristics and chaos[J]. Signal Process, 2015, 109: 119-131. DOI:10.1016/j.sigpro.2014.10.033 |
| [12] |
Souyah A, Faraoun K M. An image encryption scheme combining chaos-memory cellular automata and weighted histogram[J]. Nonlinear Dynamics, 2016, 86(1): 639-653. |
| [13] |
Xie Dong, Peng Haipeng, Li Lixiang, et al. An efficient privacy-preserving scheme for secure network coding based on compressed sensing[J]. International Journal of Electronics and Communications (AEU), 2017, 79: 33-42. DOI:10.1016/j.aeue.2017.05.028 |
| [14] |
Li Xinbin, Wang Chao, Yang Zijun, et al. Energy-efficient and secure transmission scheme based on chaotic compressive sensing in underwater wireless sensor networks[J]. Digital Signal Processing, 2018, 81: 129-137. DOI:10.1016/j.dsp.2018.07.006 |



