2. 广西交科集团有限公司, 南宁 530007
为满足海量数据处理要求,提出了一种基于网格的K-means快速聚类算法(SPGK).设计基于网格质心的聚类簇个数选取算法,对数据进行网格划分得到每个网格的质心,将质心作为K-means聚类的样本点,从而减少K-means的欧氏距离计算次数.该算法基于Spark平台实现并行计算,进一步地提高了算法的运行效率.SPGK不但能够获得良好的聚类效果,而且缩减了欧氏距离计算次数,适用于海量数据的快速聚类.在千万级数据集上的实验结果表明,SPGK的性能明显优于现有的K-means++和基于K均值聚类的递归划分方法.
2. Guangxi Jiaoke Group Company Limited, Nanning 530007, China
To meet the requirements of massive data processing, a grid-based K-means fast clustering algorithm (SPGK) is proposed. Selection for optimal clustering initial point and the number of clusters algorithm is presented. The grids of different clusters are meshed to obtain the centroid of each grid. These centroid points are used as sample points for K-means clustering, thereby reducing the number of Euclidean distance calculations of K-means. SPGK realizes parallel computation based on Spark platform, which further improves the running efficiency of the algorithm. SPGK not only obtains good clustering effect but also greatly reduces the number of Euclidean distance calculations, which is suitable for fast clustering of mass data. With 10 millions of data, the experiments show that SPGK is superior to the existing K-means++ and recursive partition based K-means clustering algorithms obviously.
随着数据的大规模增长和信息系统的云服务化, 如何利用海量数据(笔者认为数据量至少达到107以上)进行聚类挖掘从而获取有用价值, 成为目前企业取得竞争优势的重点[1].为适应107级别的数据处理, 不仅需要很大的存储空间, 而且分析、处理和检索操作都非常困难[2].如何实现海量数据的快速聚类成为当前聚类算法的研究重点.
在目前的聚类算法中, 有基于密度的带噪声的密度聚类方法[3] (DBSCAN, density-based spatial clustering of applications with noise)算法、基于空间网格的统计信息网格[4] (STING, statistical information grid)算法、层次聚类以及距离划分的K-means[5]算法.这些算法尽管理论上可以实现数据的聚类分析工作, 但是由于算法本身的特性以及技术的限制还不能适用于海量数据的处理.
K-means聚类速度快, 具有算法简单、易于实现等优势, 如今仍然广泛使用, 被列为机器学习的十大聚类算法[6]之一.然而, 随着数据量的不断增长, K-means本身的计算特点严重影响了它的聚类效果以及执行效率.首先, K-means算法和K-means++[7]等其他改进算法都面临着一个共同问题:K值的选取是随机性的.因此导致聚类无法实现快速收敛而需要多次迭代计算, 从而大幅度降低了算法执行效率.其次, K值的选择存在盲目性, 完全凭借经验或者使用其他方法, 都不高效.
近年来, 数据处理平台性能不断提升. Apache Spark[8]使用弹性分布式数据集(RDD, resilient distributed datasets)的抽象数据结构以及基于有向无环图的抽象计算流程, 极大提升了复杂机器学习和数据挖掘分析的计算性能. He等[9]提出了一种基于Spark的并行化移动对象聚集模式挖掘的RDD-DBSCAN+聚类算法, 很好地提高了聚类算法的效率.
针对当前K-means以及相关改进算法存在的不足, 笔者提出一种基于网格的K-means快速聚类算法(SPGK, Spark based parallel grid K-means).设计聚类簇的个数确定和最佳聚类初始点选取算法(GCM, grid centroid method), 在GCM基础上依据不同类簇之间的最小距离进行网格划分, 计算每个网格的质心作为K-means聚类的样本点.针对K-means需要大量计算欧氏距离的问题, 优化K-means算法聚类初始点、K值的随机选取以减少欧氏距离的计算量.基于Spark平台实现整个快速聚类算法.
1 相关工作K-means系列算法优化的研究工作主要集中在降低计算复杂度方面, 包括基于确定K值的优化方法、基于减少欧氏距离计算次数的优化方法和基于并行化的优化方法等.基于确定K值的优化方法通过提前计算获得合适的K值, 从而避免枚举K值的尝试和过多的迭代计算, 达到减少计算量的目标.确定K值的方法有手肘法[7]、Gap Statistic[10]、基于混合距离的方法(MBHD,method based on hybrid distance)[11]等算法.基于减少欧氏距离计算次数的优化方法注意到在对海量数据进行聚类时, K-means聚类算法的计算量增长很快, 其中衡量样本点间相似度的欧氏距离计算所占比例较高.为了降低K-means的算法复杂度, Capo等[12]从减少欧氏距离计算次数的角度出发, 结合网格聚类的特点, 将网格内的样本点近似成一个网格质心进行K-means聚类, 实现K-means在海量数据下的快速聚类.基于并行化的优化方法针对大数据背景下串行K-means聚类效率低下的问题, 通过对聚类过程中每一次迭代的聚类中心相关计算的并行化, 提高了K-means的可靠性和效率. Wu等[13]将K-means并行化编程后在Hadoop分布式系统中运行, 提高了算法的运行效率. Wang等[14]通过研究K-means的聚类边界问题, 使用Spark实现数据样本点间的距离计算和类簇中心点更新的并行计算.
与K-means不同, 网格聚类是一种空间数据结构聚类算法, 因而计算效率很高.通过结合网格实现海量数据的快速聚类是一种有效降低原有聚类算法复杂度的途径.徐晓等[15]在密度峰值聚类算法基础上结合网格聚类, 极大地降低了计算复杂度.于彦伟等[16]提出了一种基于网格的DBSCAN, 以实现DBSCAN的快速聚类.因此, 笔者提出方法将网格聚类思想引入K-means聚类, 提高了K值和聚类初始点选取效率, 降低了欧氏距离计算次数.
2 基于网格的K-means算法 2.1 问题描述K-means算法时间复杂度问题可以描述为
| $ t=m[ndK+ \sum\limits^ K_{ i=1} \sum\limits^ n_{ j=1} (x_{j}-c_{i})^{2}] $ | (1) |
其中:m为迭代次数, n为数据量, d为数据集维数, K为类簇个数, xj、ci分别为数据集样本点和类簇中心点.由式(1)可以得出, 当数据量级别达到107以上时, K-means对于欧氏距离的计算量达到108以上, 相当于1010级别以上的加减操作计算量.同时, K-means的聚类效果也非常依赖于K值以及聚类初始点的选取.不合适的K值和过于接近的聚类初始点都会导致迭代次数增加, 从而导致更多的计算量.
网格聚类算法复杂度只与网格个数r相关.因为r≪n, 所以网格聚类相比K-means算法速度更快.但是, 网格聚类也存在着网格划分大小选择的问题, 当划分的网格足够大时, 会出现不同类簇的样本点划分到同一簇类中心, 将增大聚类误差.
基于网格的距离划分必须考虑权重问题, 在密度不同的网格中, 聚类中心应当偏向密度较大的网格而远离密度较小的网格, 并且权值系数与密度有关.设聚类中心为ck, 网格g1、g2的密度为|g1|、|g2|且|g1|≥|g2|, 则聚类中心的计算公式为
| $ c_{i}=(g_{2}+g_{1}) \frac{{|g_{1}|}}{{ |g_{1}|+|g_{2}|}} $ | (2) |
数据集合:在一个未知簇的个数的数据集样本U中, 有U={u1, u2, …, un}, 其中un代表一个类簇集合, n为集合中数据总个数.
网格集合:将数据集合U的数据区域划分成大小相对的网格区域而得到网格集合G={g1, g2, …, gn}, 其中gx表示在网格集合G中的坐标位置且gx⊆G, x∈{1, 2, …, n}, |gx|表示gx的密度大小.
网格质心:对于网格集合G中的任意网格gx, 其网格质心计算公式为
| $ c_{i}= \frac{{1}}{{ |g_{x}|}} \sum\limits^ n_{ j=1} x_{j} $ | (3) |
其中n为网格gx的样本点个数.
簇:在集合U中, 由属于同一类的样本点xj(xj⊆U)组成的样本点集合叫作簇.而在网格集合G中, 网格的簇gk是由属于同一类网格gx的质心点构成的, 有gk={c1, c2, …, cn}.
质心中心区域:对于任意2个相邻的质心cn-1、cn都存在一个密度加权的中心距离区域, 称为质心中心区域ac.其计算公式为
| $ a_{c}=(c_{n-1}+c_{n}) \frac{{ |c_{n}|}}{{ |c_{n-1}|+|c_{n}|}} $ | (4) |
其中|gn-1|≥|gn|.
类簇中心:由属于同一簇的网格质心通过加权求得的值为类簇中心.其计算公式为
| $ s_{n}= \frac{{ 1}}{{ |s_{n}|}} \sum\limits^ n_{ x=1} |c_{x}|c_{x} $ | (5) |
其中|sn|为该簇的质心总数.
距离均方误差:由各个数据集中的样本点xj与选取中心ci的距离平方和误差得到, 用于分配样本点到最小距离的类簇中心点, 计算公式为
| $ E= \sum\limits^ K _{i=1} \sum\limits^ n_{ j=1} \min ‖x_{j}-c_{i}‖^{2} $ | (6) |
其中K为聚类个数.
2.3 网格K值和聚类中心选取算法基于网格的K值和聚类中心选取算法GCM的核心思想是:将所有的数据样本点都映射到网格中, 去除密度低于阈值的网格, 合并相似的网格, 剩下的网格数即为K值.算法步骤如下:
1) 将数据映射到初始大网格中, 求网格质心;
2) 选择任意一个未被标记的质心并标记, 搜索该质心所在网格的密度是否不低于阈值, 是则进行步骤3), 否则进行步骤4);
3) 将该网格通过四叉树算法分裂成4个新网格, 重新计算它们的质心, 然后跳转到步骤2);
4) 计算质心与其相邻的质心距离, 并通过权值距离得到中心位置区域, 判断该中心位置区域密度是否不低于密度阈值, 如果满足则标记这2个质心属于同一个簇, 否则标记为不同簇的质心;
5) 重复步骤2), 直到所有质心遍历完毕;
6) 计算得到标记为同一样本的质心之间的权值距离中心点, 得到的中心点个数为K值, 中心所在的位置为初始聚类中心点.
算法伪代码如算法1.
算法1 网格K值和聚类中心选取算法
输入:未知样本个数数据集D
输出:质心和K
1 centroids ci←gi; gi←D
2 While gi hasn’t been mark
3 foreach caculate ci←gi
4 if ci≠∅, center←ci∪ci+1
5 if center≠∅, ci, ci+1∈clusteri
6 else quadtree gi∈(1, 2, 3, 4)←gi, update ci←gi
7 else ci, ci+1∉clusteri
8 endfor
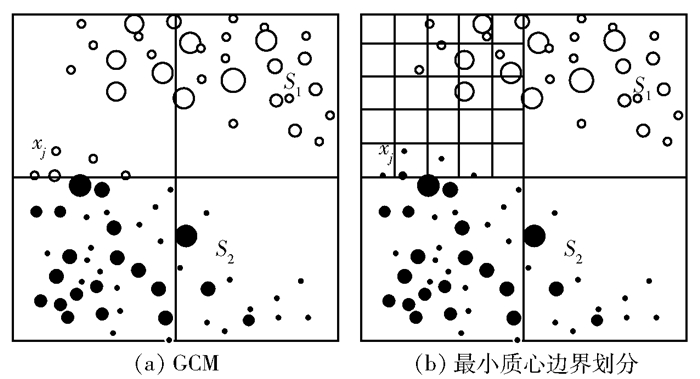
2.4 网格K-means聚类算法GCM得到K值和初始聚类中心之后, 利用初始聚类中心单次聚类可能将样本点错误划分.如图 1(a)所示, 在同一网格中属于不同簇的样本点容易被识别为同一簇, 其中xj为S2的样本点, 但是被划分成了S1的样本点.此外, 大网格划分也存在无法识别噪声点、对数据边缘识别效果差等问题.
|
图 1 网格大小划分 |
为提高聚类的准确性, 需要在原来的基础上进行更加细致的网格划分, 笔者采取基于最小质心的边界划分策略.如在图 1(a)中, xj被错误划分到S1中, 而以xj中最大值为边界进行划分时, xj便能够被正确地划分到S2中, 如图 1(b)所示.
基于网格的K-means聚类算法步骤如下:
1) 将数据样本点映射到网格中, 取得每个网格的质心点和每个网格的密度;
2) 选取最小质心网格并进行网格划分;
3) 根据选取的聚类初始中心点, 计算每个网格质心到聚类中心的欧氏距离;
4) 根据权值距离分配网格到距离最近的聚类中心点;
5) 根据权值距离重新计算新的聚类中心点;
6) 迭代, 直到所有网格到对应聚类中心的权值欧氏距离最小.
算法伪代码如算法2.
算法2 基于网格的K-means聚类算法
输入:轨迹数据集合D
输出:类簇中心和所属类簇中心网格集合
1 centroids gi←gi; gi←D
2 While gi≠∅
3 choose K and centriods ci
4 repeat
5 ci←gi
6 update E
7 until E do not change
8 endfor
2.5 算法分析2.4节设计的算法以网格质心进行K-means聚类, 减少了距离的计算次数.以下证明以质心为代表的聚类效果与基于样本点的聚类效果是一致的.
设数据样本点集合为X={x1, x2, …, xn}, 类簇中心点聚类集合为C={c1, c2, …, ck}, 网格质心集合为G={g1, g2, …, gn}, 样本点和网格质心均方误差分别为Ex、Eg.
| $ \begin{array}{c} E_{g}=\sum\limits^ k_{ i=1} \sum\limits^ n_{j=1} (g_{j}-c_{i})^{2}=\\ \sum\limits^ k_{ i=1} \sum\limits^ n_{j=1} (g^{2}_{j}-2g_{j}c_{i}+c^{2}_{i}) \end{array} $ | (7) |
| $ \begin{array}{c} E_{x}=\sum\limits^ k_{ i=1} \sum\limits^ n_{j=1} ‖x_{j}-c_{i}‖^{2}=\\ \sum\limits^ k_{ i=1} ‖x_{1}-c_{i}‖^{2}+‖x_{2}-c_{i}‖^{2}+…+‖x_{n}-c_{i}‖^{2}=\\ \sum\limits^ k_{ i=1} x^{2}_{1}-2x_{1}c_{i}+c^{2}_{i}+…+x^{2}_{n}-2x_{n}c_{i}+c^{2}_{i}=\\ \sum\limits^ k_{ i=1} \sum\limits^ n_{j=1} (x^{2}_{j}-2x_{j}c_{i}+c^{2}_{i}) \end{array} $ | (8) |
可得Eg=Ex.
2.6 算法复杂度分析1) GCM算法.与Yang等[17]提出的MBHD算法和K-means++算法中的手肘法进行对比.假设在一个数据集合U中, 样本点个数为n, 数据维度为d, 算法执行次数为m, 则3种算法的计算复杂度均可表示为O=m(ndk).假设数据集合U的样本点个数n的数量级达到107, K值为5, 维度为2, 以欧氏距离计算次数衡量算法复杂度, 则MBHD计算次数为6.0×107, 手肘法在每次都能取到最小E的情况下最小计算次数为1×109, 而GCM的最大计算次数仅为48次, 不到MBHD的百万分之一, 手肘法的两千万分之一.
2) 网格K-means聚类算法.与Capo等[12]提出的基于K均值聚类的递归划分方法(RPKM,recursive partition based K-means)以及K-means++算法进行对比.对于一个样本点个数为10 000, 维度为2的集合, K-means++运算次数为6.42×105, RPKM运算次数为2.68×104, 而所提出的算法运算次数为3.97×102, 是K-means++算法的0.062%, RPKM算法的1.5%.
3 实验及分析 3.1 实验环境为验证所提出的基于网格的K-means算法的有效性, 分别采用人工数据集和UCI数据集进行实验.此外, 由于Spark是基于Scala语言设计的, 并且与其他语言相比兼容性更好, 因此实验采用Scala编程实现.实验用到1台普通计算机和4台工作站, 机器配置如表 1所示.实验使用Scala2.11.8进行开发, 集群环境为Spark 2.2.0, 运行模式为Spark on yarn.
|
|
表 1 机器配置表 |
基于K-means++的手肘法、MBHD算法均执行10次以上并选取最小的E作为实验数据, K-means++手肘法的值从2开始选取, 实验结果如图 2所示.
|
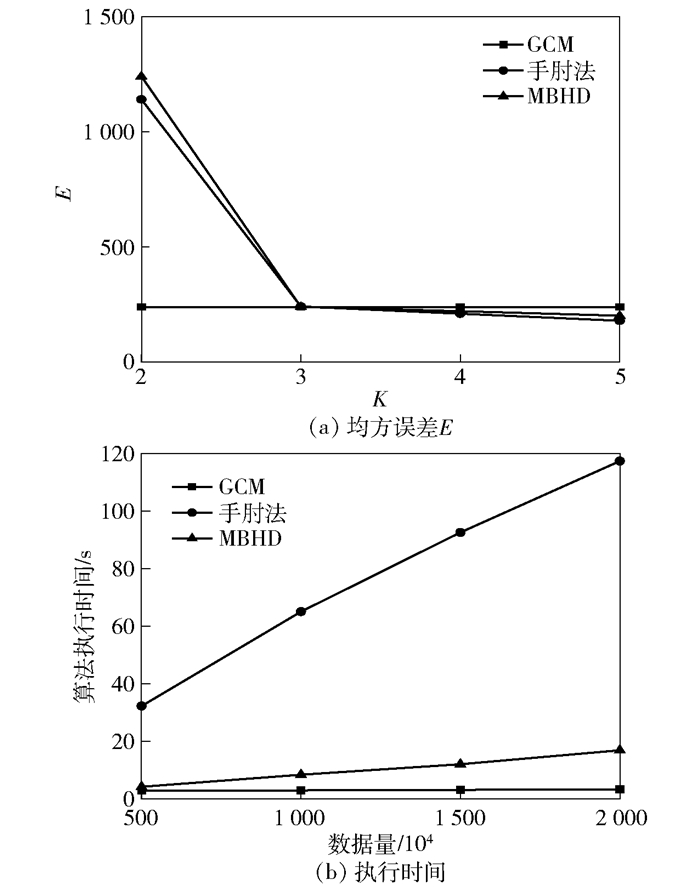
图 2 GCM、手肘法、MBHD算法性能对比 |
由图 2(a)可知, 在手肘法和MBHD的折线中, K=3时E的值快速下降, 选取K值为3.而GCM算法在K=3时与手肘法相交, K值也为3, 从而验证了该算法的准确性.变化数据量分别对500万、1 000万、1 500万以及2 000万进行实验, 由图 2(b)可知GCM执行时间低于手肘法以及MBHD.所以, GCM算法与手肘法、MBHD算法对比, 在准确度相同的情况下缩减了计算时间, 提高了效率.
3.3 SPGK性能分析为验证所提出的SPGK算法性能, 分别采用人工数据集以及UCI库中的葡萄酒数据进行实验, 而且将2种数据都扩大到{104, 105, 106, 107}条.首先在人工数据集下进行实验, 结果如图 3所示.
|
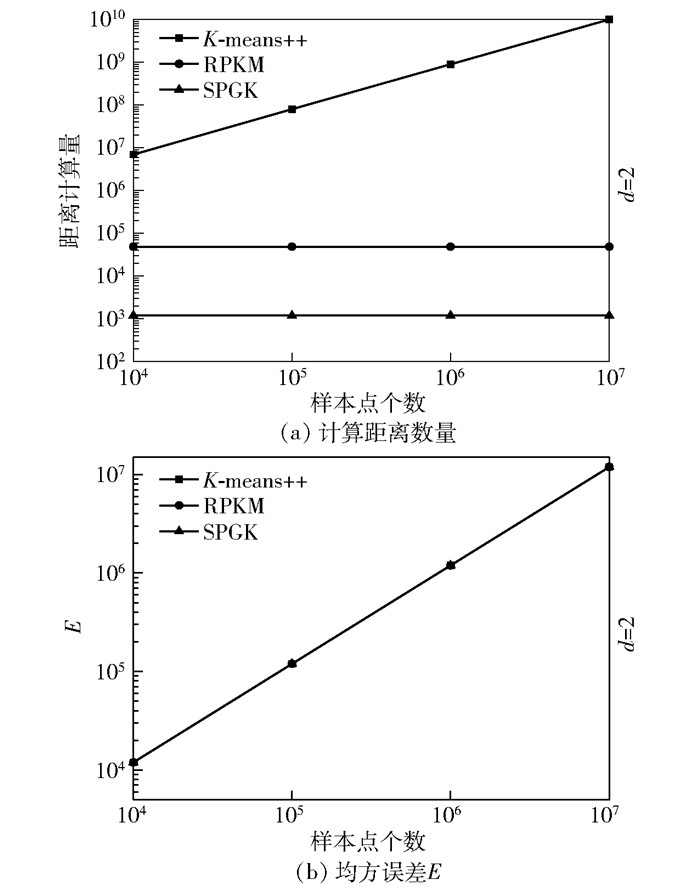
图 3 K-means++、RPKM、SPGK性能对比(人工数据集) |
由图 3(a)可知, SPGK的欧氏距离计算量要小很多, 同时RPKM算法和SPGK算法都能够在数据大量增长的情况下依然保持欧氏距离计算次数不变.这是由于这2种算法都是以网格质心为代表进行K-means聚类的, 网格聚类的复杂度只与网格个数有关, 因而不影响算法的执行效率.
如图 3(b)所示, 对RPKM和K-means++算法进行了10次实验,并取其中最小一次的E作为实验结果, 而SPGK算法只执行了一次, 就取得了与执行多次RPKM、K-means++算法一致的实验结果.其原因是SPGK算法在GCM中已经获得了准确的簇的个数和最佳聚类初始中心点, 所以可以极大地减少K-means在计算欧氏距离时的次数.在图 3中, 当数据量为107个时, K-means++需要运行10次以上, 欧氏距离的计算次数达到108以上;尽管RPKM也采用了网格划分的方式,在一定程度上减小了计算欧氏距离的次数, 但是随着不断地进行二分裂划分, 计算次数呈指数级增长, 计算次数也达到了104次;而SPGK算法一直维持在102级数上.该实验结果说明,RPKM和SPGK算法的时间复杂度都不会随着实验数据的增长而受影响, 两者的时间复杂度只与网格的个数有关, 因此具备处理海量数据的能力, 同时SPGK算法性能更优.值得一提的是, 笔者也对SPGK进行了多次实验, 结果发现SPGK的E值不会改变, 并且E值与RPKM、K-means++的E值相等(在10-13的位数上可能不同).这也进一步验证了SPGK算法在提高计算速度的同时, 仍保持了良好的聚类效果.
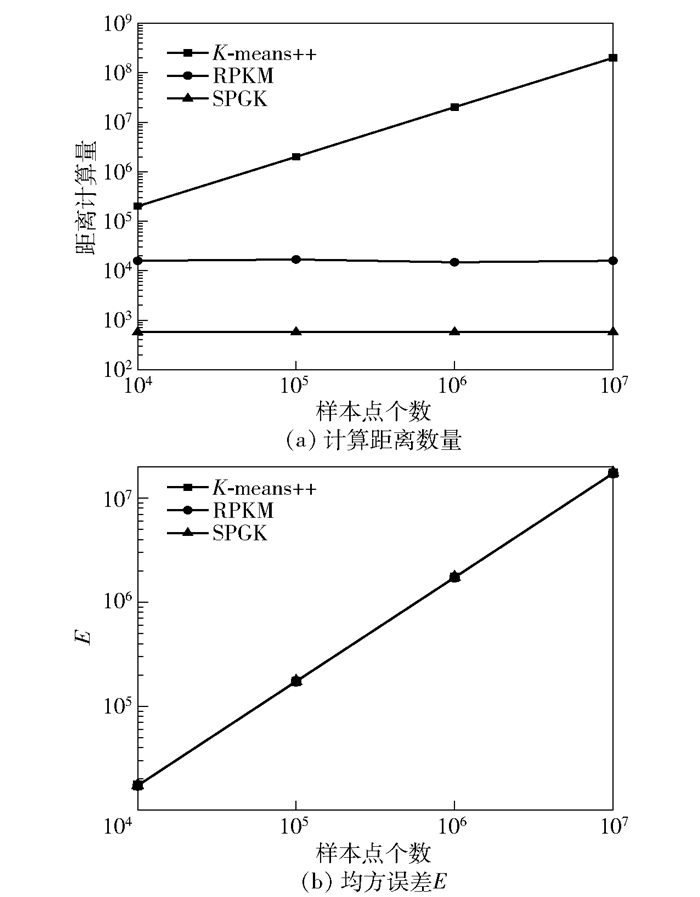
进一步使用UCI中的数据集进行验证, 实验结果如图 4所示. SPGK的计算效率依然比RPKM和K-means++算法高, 和人工数据集分析结果一致.
|
图 4 K-means++、RPKM、SPGK性能对比(UCI数据集) |
针对K-means系列算法在海量数据条件下存在运行效率低、得到的聚类结果可能不是局部最优解等问题, 提出了一种海量数据快速聚类算法.提出聚类簇的个数确定和选取最佳聚类初始点算法, 提高了K-means的聚类效果; 依据不同类簇之间的最小距离对数据进行网格划分, 计算每个网格的质心作为K-means聚类的样本点, 提高了K-means算法的运行速度, 且算法的复杂度与原始数据的数量无关.基于Spark平台实现了整个快速聚类算法, 实验结果表明,SPGK不仅能够处理海量数据并且得到了良好的聚类效果, 明显优于现有的K-means++和RPKM聚类算法, 在大数据分析中具有广阔的应用前景.
| [1] |
Gahar R M, Arfaoui O, Hidri M S, et al. An ontology-driven MapReduce framework for association rules mining in massive data[J]. Procedia Computer Science, 2018, 126: 224-233. DOI:10.1016/j.procs.2018.07.236 |
| [2] |
Hidri M S, Zoghlami M A, Ayed R B. Speeding up the large-scale consensus fuzzy clustering for handling big data[J]. Fuzzy Ets and Systems, 2018(348): 50-74. |
| [3] |
Ester M, Kriegel H P, Xu X. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//International Conference on Knowledge Discovery & Data Mining. New York: ACM, 1996: 226-231. https://www.researchgate.net/publication/221653977_A_Density-Based_Algorithm_for_Discovering_Clusters_in_Large_Spatial_Databases_with_Noise
|
| [4] |
Wang W. STING:a statistical information grid approach to spatial data mining[J]. Proc of Very Large Database Conf, 1997(15): 186-195. |
| [5] |
Hartigan J A, Wong M A. A K-means clustering algorithm[J]. Journal of the Royal Statistical Society:Series C (Applied Statistics), 1979, 28(1): 100-108. |
| [6] |
Wu X, Kumar V, Ross J, et al. Top 10 algorithms in data mining[J]. Knowledge And Information Systems, 2007(14): 1-37. |
| [7] |
Arthur D, Vassilvitskii S. K-means++:the advantages of careful seeding[J]. Proceedings of Theghteenth Annual Acm Siam Symposiumon Discrete Algorithms Society for Industrial & Applied Mathematics, 2007, 11(6): 1027-1035. |
| [8] |
Shmeis Z, Jaber M. Fine and coarse grained composition and adaptation of spark applications[J]. Future Generation Computer Systems, 2018, 629-640. |
| [9] |
He Qian, Chen Yiting, Dong Qinghe, et al. A parallel clustering and test partitioning techniques based mining trajectory algorithm for moving objects[C]//2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD). Guilin: Cuilin University of Electronic Technology, 2017: 455-462. https://www.researchgate.net/publication/326428504_A_parallel_clustering_and_test_partitioning_techniques_based_mining_trajectory_algorithm_for_moving_objects
|
| [10] |
Tibshirani R, Hastie W T. Estimating the umber of clusters in a data Et via the gap statistic[J]. Journal of the Royal Statistical Society, 2001, 63(2): 411-423. DOI:10.1111/1467-9868.00293 |
| [11] |
Ishioka T. Extended K-means with an efficient estimation of the number of clusters[C]//Intelligent Data Engineering & Automated Learning-ideal, Data Mining, Financial Engineering, & Intelligent Agents, Second International Conference. HongKong: Morgan Kautmann Publishs Inc, 2000. https://www.researchgate.net/publication/221253079_Extended_K-means_with_an_Efficient_Estimation_of_the_Number_of_Clusters
|
| [12] |
Capo M, Perez A, Lozano J A. An efficient approximation to the K-means clustering for massive data[J]. Knowledge-Based Systems, 2017, 117(2): 56-69. |
| [13] |
Wu Kehe, Zeng Wenjing, Wu Tingting, et al. Research and improve on K-means algorithm based on hadoop[C]//IEEE International Conference on Software Engineering & Service Science. Piscataway: IEEE, 2015: 334-337. https://www.researchgate.net/publication/308728639_Research_and_improve_on_K-means_algorithm_based_on_hadoop
|
| [14] |
Wang Bowen, Yin Jun, Hua Qi, et al. Parallelizing K-Means Based Clustering on Spark[C]//International Conference on Advanced Cloud and Big Data. Piscataway: IEEE, 2016: 31-36. https://www.researchgate.net/publication/312487404_Parallelizing_K-Means-Based_Clustering_on_Spark
|
| [15] |
徐晓, 丁世飞, 孙统风, 等. 基于网格筛选的大规模密度峰值聚类算法[J]. 计算机研究与发展, 2018, 55(11): 79-89. Xu Xiao, Ding Shifei, Sun Tongfeng, et al. Large-scale density peaks clustering algorithm based on grid screening[J]. Journal of Computer Research and Development, 2018, 55(11): 79-89. |
| [16] |
于彦伟, 贾召飞, 曹磊, 等. 面向位置大数据的快速密度聚类算法[J]. 软件学报, 2018, 29(8): 2470-2484. Yu Yanwei, Jia Zhaofei, Cao Lei, et al. Fast density-based clustering algorithm for location big data[J]. Journal of Software, 2018, 29(8): 2470-2484. |
| [17] |
Yang Jie, Ma Yan, Zhang Xiangfen, et al. An initialization method based on hybrid distance for K-means algorithm[J]. Neural Computation, 2017, 29(11): 3094-3117. DOI:10.1162/neco_a_01014 |


