针对膝关节与假体空间坐标系不一致的问题,提出了一种基于主成分分析(PCA)与迭代最近点(ICP)算法相结合的三段式配准方法.采用PCA结合两次ICP算法的配准策略,对膝关节与关节假体的点云数据进行PCA配准处理,然后对得到的初始配准结果采用ICP算法进行调整,最后对调整好姿态的点云数据再次进行ICP配准,从而将其空间坐标轴调整到一致.实验结果表明,三段式配准方法相较于其他算法,可在保持较高配准精度的同时缩短配准时间.
In view of inconsistency between knee joint and prosthesis in spatial coordinate system, a three-stage registration method based on principal component analysis (PCA) and iterative closest point (ICP) algorithm is proposed, which adopts PCA and ICP twice. Firstly, the point cloud data of knee joint and joint prosthesis is registered by PCA. then ICP algorithm is used to adjust the initial registration results. Finally, ICP registration is carried out again for the adjusted point cloud data, so as to adjust its spatial coordinate axis to be consistent. Experiments show that compared with other algorithms, the three-stage registration method can keep high registration accuracy and shorten the registration time.
目前,人工关节置换术已经成为治疗严重关节病变的常用手段之一,手术采用人造关节假体来替换患者已经破损、坏死的关节组织.标准的关节假体均为系列生产,很难做到按患者骨骼特点“量体裁衣”,因此患者都是在一定的范围内选用.如何选取最适合的人工假体是关节置换手术的一个重要问题.常用的做法是在手术之前,医生通过患者膝关节的二维影像信息结合自身经验来选取适用的假体型号,再对关节进行打磨以适用假体.但是二维图像包含信息有限,利用二维图像重构的三维图像可以为临床提供更丰富的信息,将膝关节与假体的三维图像进行配准,然后对同一坐标系下的二者进行匹配操作,可实现在术前对假体适用度的判断.
三维点云配准问题的本质是空间变换,是求解不同点云间旋转平移矩阵的一个数学计算过程.针对点云的配准问题,Besl等[1]在1992年提出的迭代最近点(ICP, iterative closest point)算法是目前使用最为广泛且最为经典的三维点云配准算法. ICP算法具有较高的精度和较快的配准速度,适用于多种领域,但存在对初始值依赖过高的问题.针对此问题,大多数学者采用将配准流程分为粗配准和精配准两阶段的解决方法,如Chen等[2]采用了两阶段ICP(TICP, two-stage ICP)算法,利用第1阶段的ICP算法结果作为第2阶段ICP配准的初始状态,有效缓解了ICP算法对待配准点云初始状态要求高的问题,同时也减少了配准中迭代循环的次数,降低了时间消耗.随后,盖宇[3]在此基础上采用最大期望ICP算法代替ICP算法作为初始配准,对TICP算法进行了改进,加快了整个配准流程的速度. 2017年,杨飚等[4]在“粗”“精”配准过程中间新加入了“微调”这一过程,对粗配准的结果做进一步的调整和改善,为精确配准阶段提供了更加精准的初始配准状态.实验中采用正太分布变换(NDT, normal distributions transform)算法与2次ICP算法相结合,实现了对点云的快速配准.
基于以上的研究,笔者提出了一种主成分分析(PCA, principal component analysis)和ICP结合的三段式膝关节配准算法.配准流程大致为“PCA粗配准—ICP配准—ICP再次配准”,算法利用PCA的快速配准特性改善ICP耗时长的问题并为ICP提供可靠的初始值,同时ICP的配准精确性也避免了单独使用PCA算法得到的配准结果精度不够的问题.
1 相关基础工作 1.1 PCA算法原理与流程PCA算法是常用的降维方法之一[5-6],它的中心思想是将检测到的n维数据特征映射到k(k<n)维特征空间上,而且对原始数据信息并没有产生破坏,从而实现高维数据的降维处理.其中全新的K维特征称为主成分,是基于原始数据构造出来的. PCA算法的理论推导分为两种:最大方差理论和最小二乘法.依据最大方差理论,PCA的分析过程即是寻求一个最优子空间,在该空间内n维特征转化为k维特征时,得到的每一维方差都很大.具体的算法流程如下.
1) 假设有n维样本集D ={x1, x2, …, xn},首先对样本集中所有样本进行中心化处理:
| $ x_{i}=x_{i}- \frac{{1}}{{ n}} \sum\limits^ n_{ j=1} x_{j} $ | (1) |
2) 然后计算样本集的协方差矩阵XXT,并对矩阵进行特征值分解,得到特征值;
3) 将特征值从大到小排序,取前k个特征值所对应的特征向量(ω1, ω2, …, ωk),对特征向量进行标准化处理,然后组成向量矩阵W;
4) 将原样本集D中的每一个样本xi转化为新样本yi= WTxi;
5) 降维后样本集表示为D ′={y1, y2, …, yk}.
1.2 ICP算法原理与流程ICP算法的本质是基于最小二乘法的最优匹配算法[7].对于浮动图像与参考图像,将其用坐标表示为P =(Pi, i=1, 2, …, N)和Q =(Qj, j=1, 2, …, M),假设2组数据中共存在S对对应点,旋转矩阵表示为R,平移向量表示为T,那么ICP算法的核心就是使所有对应点之间的欧氏距离的二次方和最小,即为式(2)的目标函数最小.
| $ f( \boldsymbol{R}, \boldsymbol{T} )= \frac{{ 1}}{{ S}} \sum\limits^ S_{ l=1 }|Q^{k}_{l}- \boldsymbol{R} P^{k}_{l}- \boldsymbol{T} |^{2} $ | (2) |
其中Qlk与Plk是一对对应点.
算法[8]的步骤主要是一个“寻找对应点—求解变换参数R和T—代入式(1)—结果小于阈值停止,否则继续寻找对应点……”的循环求解过程.首先对浮动图像P上的每一个点,在参考图像Q上找到距离它最近的点作为对应点,得到对应点集合;然后利用四元数法求取变换参数R和T;最后将求取的R和T代入式(2),求取结果小于阈值停止迭代,否则返回求取对应点,继续求取变换参数.
对比2种算法来看,对于2组相似度高的空间数据,PCA获取的主分量之间的变换关系可以近似等于两组数据坐标系之间的变换关系,可以较快地获取转换矩阵,但对于相似度不够大的数据,获取的转换矩阵存在一定偏差,配准结果不够精确;ICP算法通过每次迭代,使浮动数据集更加接近参考数据,但算法本身在寻求对应点时耗费时间久,如果初始情况两组数据相差较大,迭代次数也会相应增加.
针对PCA和ICP算法的原理特性,提出了PCA结合两次ICP算法的三段式三维膝关节配准方法.三段式的配准算法结合了PCA算法的快速配准特性和ICP算法的配准精度高的优点,采用PCA—ICP—再次ICP的配准流程进行配准.首先采用PCA算法对两组经过下采样处理后的点云数据进行粗配准,得到一个初始的转换矩阵;然后依据初始矩阵更新浮动数据,对更新后的浮动数据与参考数据做基于ICP算法的配准处理,调整初始转换矩阵;最后将调整后的初始转换矩阵作用在原始浮动数据上,再次采用ICP算法对原始点云数据进行精确配准,将两组数据的坐标系转换为统一坐标系.
2 三步式配准算法将膝关节和关节假体做三维重建,重建后的数据以点云形式输出.膝关节图像数据作为配准中的参考数据,关节假体图像数据作为浮动数据.其中,浮动数据共有N个点,表示为P =(Pi, i=1, 2, …, N);参考数据共有M个点,表示为Q =(Qj, j=1, 2, …, M).两组数据的点数未必相同.
2.1 基于PCA算法的粗配准对两组图像数据做基于PCA算法的粗配准,算法的主要思想是[9]:先对两组点云数据进行PCA,获得主要组成部分,然后利用主要组成部分和质心坐标构造矩阵,最后计算矩阵之间的变换关系以获得初始变换矩阵.实现步骤如下.
1) 样本中心化.以浮动图像为例,将P中数据点坐标排列成矩阵X,即
| $ \boldsymbol{X} = \left[ \begin{array}{*{35}{l}} {x_{1}} & {…}& {x_{n}} \\ {y_{1}} & {…}& {y_{n}} \\ {z_{1}} & {…}& {z_{n} } \end{array} \right] $ | (3) |
其中每列为1个点坐标.
求解每一行的平均值x, y, z,中心化处理后的矩阵表示为
| $ \boldsymbol{X} _{1}= \left[ \begin{array}{*{35}{l}} {x_{1}- \bar x} & {… }& {x_{n}-\bar x } \\ {y_{1}-\bar y } & {…}& { y_{n}-\bar y } \\ {z_{1}-\bar z} & { …}& {z_{n}-\bar z} \\ \end{array} \right]=\left[ \begin{array}{*{35}{l}} {x′ _{1}} & {…}& {x′ _{n}} \\ {y′ _{1}} & {…}& {y′ _{n}} \\ {z′ _{1}} & {…}& {z′ _{n}} \\ \end{array} \right] $ | (4) |
2) 计算协方差矩阵M = X1X1T.
3) PCA:对M进行特征值分解,因为是三维数据,所以只取最大的前3个特征值即可,记为λ1, λ2, λ3,且λ1>λ2>λ3,对应的特征向量分别为η1, η2, η3.
4) 计算重心坐标,记为x.
5) 计算构造矩阵.依据特征向量和重心坐标构造浮动图像的构造矩阵,表示为
| $ \boldsymbol{W} _{1}=[ \boldsymbol{\eta } _{1}, \boldsymbol{\eta} _{2}, \boldsymbol{\eta} _{3}, \boldsymbol{\bar x} ] $ | (5) |
以此类推,参考图像数据集的最大特征值对应特征向量表示为ξ1, ξ2, ξ3,重心坐标表示为y,则它的构造矩阵表示为W2=[ξ1, ξ2, ξ3, y].那么,即可求得两组点云数据间的转换矩阵为
| $ \boldsymbol{T} _{0}= \boldsymbol{W} ^{-1}_{1} \boldsymbol{W} _{2} $ | (6) |
粗配准阶段主要是为了缩短两组点云数据空间上的距离,校正其空间位置的差异,以便于接下来的配准.所以在此阶段可将两组点云进行下采样处理,减少点云的数据量,缩短粗配准所用时间.
2.2 基于ICP算法的微调使用ICP算法来求解两组数据间的转换关系,首先需要假设输入数据粗略对齐,在此假设下,通过查询目标数据上的最近点,可以得到一组对应关系.在收敛保证前提下,通过交替求解最近的对应关系和最优的刚性变换,计算出局部最优配准. ICP算法需要一个良好的初始值,但是第1阶段的PCA处理结果不能保证将待配准数据调整到最佳状态,因此在第1阶段配准结果的基础上,再次采用ICP算法进行调整,可以确保在接下来的配准中待配准数据处于一个良好的位姿状态.该阶段的目的是为接下来的精确配准提供更加良好的初始配准状态,所以可继续采用精简点云,加快整体配准速度.如果第1阶段的配准结果已经达到要求,那么第2阶段的微调及接下来的第3阶段精确配准会进一步提高配准的精度和速度;如果没有达到要求,那么微调阶段可以对它进行有效的补充和改善,为精细配准提供更加精确的初始值.
基于ICP算法的配准步骤如下.
1) 寻找对应点.依据前一步的粗配准结果,对浮动图像P进行变换,得到新的浮动图像P1,对于P1中的每一个点,在参考图像Q中找寻与之距离最近的点,即为对应点.
2) 优化粗配准得到的转换矩阵.根据步骤1)得到的对应点求取旋转和平移的参数,由于对应点对数量庞大,而旋转和平移的参数只有6个,所以可以利用四元数算法来计算新的旋转平移参数.
3) 算法迭代.根据步骤2)得到的新的旋转矩阵R和平移向量T,更新点集P1= RP+T.
4) 计算目标函数值:
| $ f( \boldsymbol{R}, \boldsymbol{T} )= \frac{{1}}{{ S }} \sum\limits^ S_{ l=1 }|Q^{k}_{l}- \boldsymbol{R} P^{k}_{l}- \boldsymbol{T} |^{2} $ | (7) |
如果结果大于规定的阈值,则返回步骤1);如果低于或迭代次数超过指定的次数,则停止计算.
2.3 基于ICP算法的精确配准ICP算法配准精度高,适用面广泛,但是在不知道精确的对应点前提下,ICP算法只能一步一步迭代地求取最优的对应点对,迭代次数多,计算代价大,所以ICP算法需要有一个良好的初始变换.初始变换的好坏直接影响配准结果的精确度,不好的初始变换会加大迭代所需次数,浪费配准时间,还有可能使点云数据局部收敛,影响配准效果.
经过前2个阶段对待配准点云的调整和处理,待配准点云已经拥有良好的位姿状态,可作为ICP算法的初始值,做基于ICP算法的精确配准.在标准ICP算法中,假设待配准数据是真包含于参考数据中,也就是说待配准数据上的点,在参考数据中有且只有一个对应点.它的工作原理即是不断地更新浮动图像的位置,直到浮动图像上的点与参考图像上对应点之间的距离达到某阈值为止.对于两组点云数据,经过前2个阶段的调整,再次应用ICP算法进行配准,可以使空间中两组点云的坐标系几乎是一致的,即可获得更准确的配准水平.
3 实验结果与分析实验运行的环境如下.
硬件环境:Intel Core i7-4500 CPU @ 1.80 GHz处理器,8 GB内存;
软件环境:Windows 7,64位操作系统;
编程环境:MATLAB R2017a.
实验数据主要是三维重建后人体膝关节的CT数据,可通过对旋转矩阵的误差分析进行测试结果的评估.由于浮动图像是参考图像经过指定的旋转矩阵转换得到的,所以转换矩阵已知,通过配准后得到的转换矩阵与已知矩阵的误差值,可以作为评价所提算法配准效果的标准.
3.1 膝关节图像配准对膝关节三维图像进行配准主要是为了验证所提出算法的可行性.实验1的数据如图 1所示.其中,图 1(a)所示为实验中的浮动数据,图 1(b)所示为图 1(a)中点云模型绕z轴旋转30°、平移向量为[5, 5, 10]转换后的点云模型,可作为实验中的参考数据.
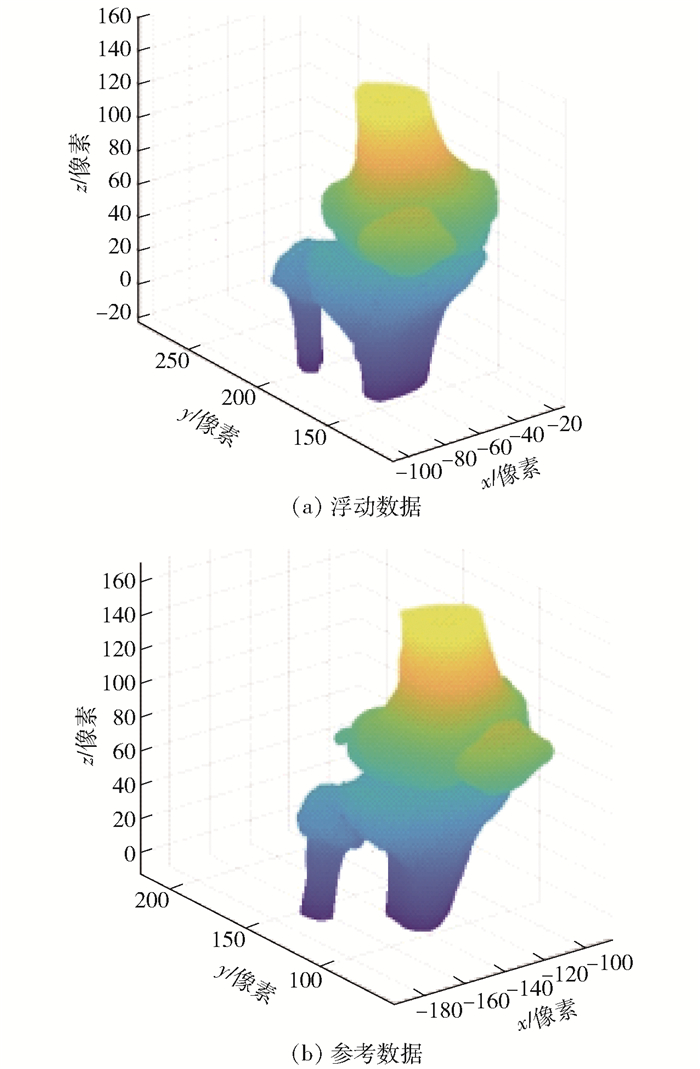
|
图 1 实验1的数据 |
三段式配准算法的配准过程与结果如下.
1) 基于PCA算法的粗配准
第1阶段,首先对两组数据进行下采样,将点云数据量缩小到原点云数据的5%,然后进行基于PCA算法的粗配准,结果如图 2所示.
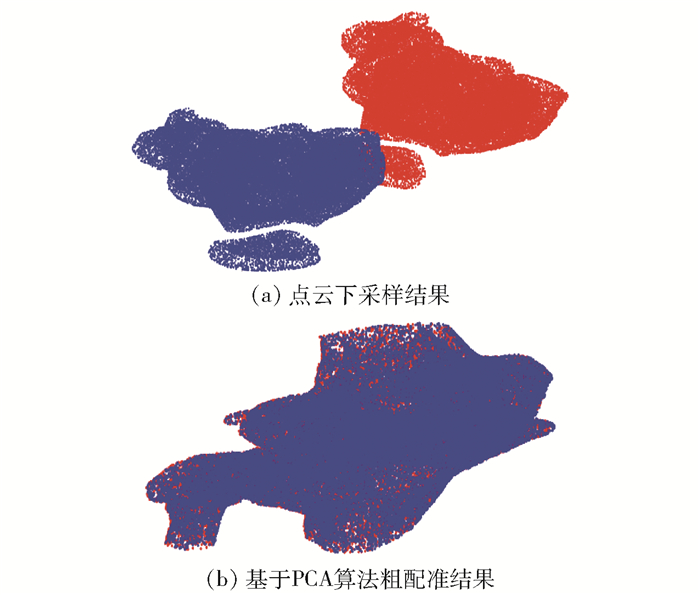
|
图 2 基于PCA算法的粗配准 |
2) 基于ICP算法的微调
第2阶段,在第1阶段的配准结果基础上,采用ICP算法做进一步的调整工作.此阶段中使用的数据仍然是下采样后的数据,结果如图 3(a)所示.
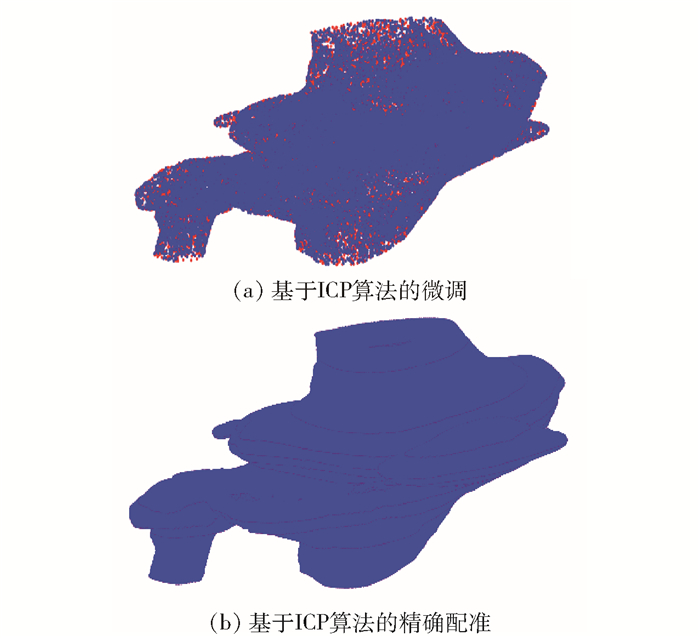
|
图 3 第2、第3阶段配准结果 |
3) 基于ICP算法的精确配准
第3阶段,将在微调阶段中获得的转换矩阵作为初始值,对数据做基于ICP算法的精确配准.在精确配准阶段,浮动数据和参考数据均采用未经过下采样处理的原始数据,结果如图 3(b)所示.
从图 2和图 3中的结果来看,经过粗配准、微调和精确配准3个阶段之后,两组点云数据在空间上基本重合,验证了实验1的可行性.另外,实验1中设定的原始旋转平移矩阵和经过配准之后计算出的旋转平移矩阵分别为
| $ \boldsymbol{A}=\left[\begin{array}{cccc} 0.866\;0 & 0.500\;0 & 0 & 0 \\ -0.500\;0 & 0.866\;0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 5 & 5 & 10 & 1 \end{array}\right] $ |
| $ \boldsymbol{B}=\left[\begin{array}{cccc} 0.866\;0 & 0.500\;0 & 0 & 0 \\ -0.500\;0 & 0.866\;0 & 0 & 0 \\ 0 & 0 & 1.000\;0 & 0 \\ 4.999\;8 & 5.000\;0 & 9.972\;3 & 1 \end{array}\right] $ |
平移误差为[-0.000 2 0 -0.027 7],可满足大部分实际需求,由此可证明所提算法的可行性.
3.2 膝关节与模拟关节假体配准膝关节作为人体最大、解剖结构最为复杂的关节组织,其人工关节假体也由多部分组成,其中的股骨假体贴合于患者的膝关节股骨下端关节面,形状类似于给膝关节的股骨端带上一个套子.以患者股骨下端部分数据建立三维模型,用来模拟膝关节假体中的股骨假体部分,作为实验中的浮动图像;截取膝关节三维点云数据中的股骨部分,绕z轴逆时针旋转30°,平移向量为[5, 5, 10],作为参考图像.实验2的数据如图 4所示.
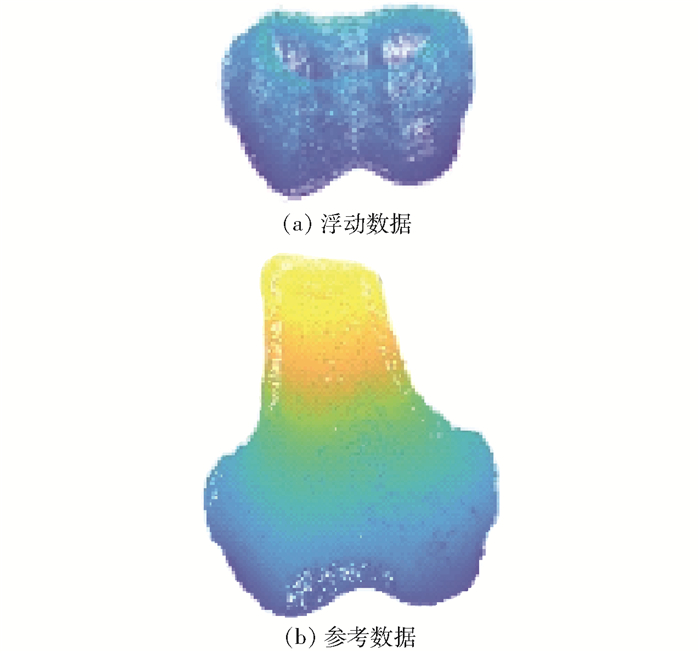
|
图 4 实验2数据 |
所提出的三段式三维膝关节配准方法的配准过程和配准结果如图 5所示.

|
图 5 模拟人工关节假体与膝关节配准过程 |
此外,为了验证所提算法的实用性,将所提算法与经典的ICP算法和杨飚等[4]提出的NDT与TICP相结合的配准(NDT+TICP)算法做了对比,对配准时间与配准精度分别做了记录,3种算法的配准所用时间对比如表 1所示.
|
|
表 1 所用时间对比 |
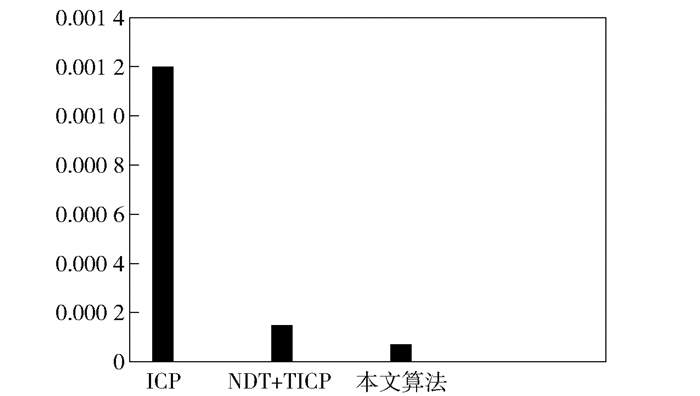
由于实验2中使用的浮动数据是被参考数据截取并按照给定原始变换矩阵变换得到的,所以可用配准后得到的转换矩阵与原始矩阵A做差值,得到变换矩阵的误差值来衡量配准结果的精度:误差值越接近于0,说明浮动数据经过变换后与参考数据越接近,也就表明此种配准算法的配准精度越高. 3种算法得到的变换矩阵误差值对比如图 6所示.
|
图 6 3种算法的变换矩阵误差值对比 |
表 1所示为对配准的时间的记录和对比.从时间来看,3种算法所耗费时间按照从小到大排序为所提算法、NDT+TICP算法、ICP算法. 图 6所示为对配准结果精度的记录和对比.在配准精度方面,所提算法精度较NDT+TICP算法精度稍高,预先不知初始转换矩阵的标准ICP算法精度最差.综合时间与精度来看,所提出的PCA结合ICP的三段式配准算法相较于NDT+TICP算法在配准时间上耗时更短,且配准精度更高.
4 结束语笔者主要研究了基于PCA和ICP的三维膝关节配准问题,结合PCA和ICP算法的特点,提出了基于PCA和ICP的三段式三维膝关节配准算法.首先,通过PCA算法粗略地配准数据以获得初始转换参数,将待配准数据进行转换更新;然后,将更新过后的待配准数据与参考数据作为初始值应用ICP算法进行进一步调整,得到调整之后的数据结果;最后,依据调整之后的结果,采用ICP算法对数据进行最终的配准处理,将膝关节点云数据与关节假体点云数据的空间坐标系调整到一起.通过对膝关节与膝关节的配准应用、膝关节与模拟关节假体的配准应用2组的实验结果表明,所提算法可对膝关节与关节假体的三维点云数据进行精确配准.同时,通过与其他经典配准算法做实验对比来看,所提算法在保证配准精度的同时可以缩短配准的时间.
| [1] |
Besl P J, McKay N D. A method for registration of 3D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. DOI:10.1109/34.121791 |
| [2] |
Chen H, Bhanu B. Contour matching for 3D ear recognition[C]//Proceedings of IEEE Workshop on Application of Computer Vision. California: University of California 2005: 123-128. https://www.researchgate.net/publication/220939515_Contour_Matching_for_3D_Ear_Recognition
|
| [3] |
盖宇. 基于两步式迭代最近点的三维人耳配准算法[J]. 微型机与应用, 2015, 34(15): 22-25. Gai Yu. 3D human ear registration algorithm based on two-step iterative closest point[J]. Microcomputer and Applications, 2015, 34(15): 22-25. |
| [4] |
杨飚, 李三宝, 王力. 基于正态分布变换与迭代最近点的快速点云配准算法[J]. 科学技术与工程, 2017, 17(15): 91-95. Yang Biao, Li Sanbao, Wang Li. Fast point cloud registration algorithm based on NDT and ICP[J]. Science and Technology and Engineering, 2017, 17(15): 91-95. |
| [5] |
严剑锋, 邓喀中. 基于PCA和Delaunay剖分点云配准算法研究[J]. 现代测绘, 2016, 39(1): 29-32. Yan Jianfeng, Deng Kazhong. Research on point cloud registration algorithm based on PCA and delaunay[J]. Modern Surveying and Mapping, 2016, 39(1): 29-32. |
| [6] |
王育坚, 吴明明, 高倩. 基于保局PCA的三维点云配准算法[J]. 光学技术, 2018, 44(5): 562-568. Wang Yujian, Wu Mingming, Gao Qian. 3D point cloud registration algorithm based on locality preserving PCA[J]. Optical Technology, 2018, 44(5): 562-568. |
| [7] |
熊风光.三维点云配准技术研究[D].太原: 中北大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10110-1018186476.htm
|
| [8] |
赵夫群, 贾一婷. 基于几何属性和改进ICP的点云配准方法[J]. 信息技术, 2019, 43(4): 33-38. Zhao Fuqun, Jia Yiting. Point cloud registration method based on geometric attributes and improved ICP[J]. Information Technology, 2019, 43(4): 33-38. |
| [9] |
翁飞, 侯文广, 曾明平. 用于三维医学图像配准的"粗精"混合算法研究[J]. 北京生物医学工程, 2016, 35(1): 12-17. Weng Fei, Hou Wenguang, Zeng Mingping. A 'coarse and fine' hybrid algorithm for three-dimensional medical image registration[J]. Beijing Biomedical Engineering, 2016, 35(1): 12-1. |


