2. 中南大学 自动化学院, 长沙 410083;
3. 中南大学 计算机学院, 长沙 410083
能量受限协作中继网络频谱利用率低,生存周期短,无线信道开放性所带来的物理层安全受到威胁,对此,将功率信标辅助射频能量采集技术、认知无线电技术和协作中继网络相结合,构建了一种新的中继节点分散布置的能量收集2跳认知协作中继网络;引入单窃听节点对第2跳传输进行窃听,并结合主动和被动窃听方式提出了最优中继选择和次优中继选择方式,推导了2种中继选择方式下次网络安全中断概率闭合式.数值计算和仿真结果表明,主接收节点和中继数目、中继和窃听节点位置设置、能量采集比例、能量转换效率以及信道容量和安全容量阈值都会对次网络安全中断性能产生显著影响.最优中继选择方式下的次网络安全中断性能明显优于次优中继选择方式.功率信标信号功率或干扰约束的增大使得次网络安全中断概率降低,并趋于饱和.
2. School of Automation, Central South University, Changsha 410083, China;
3. School of Computer Science and Engineering, Central South University, Changsha 410083, China
Aiming at the problems of low spectrum utilization, short lifetime and the physical layer security caused by the openness of the wireless channel of energy-constrained cooperative relay network, a new two hop cognitive cooperative relay network with distributed relay nodes is constructed by combining power beacon assisted RF energy collection technology, cognitive radio technology and cooperative relay network. Then, a single eavesdropping node is introduced to eavesdrop the second hop transmission, and the optimal relay selection and the sub optimal relay selection are proposed in combination with the active and passive eavesdropping modes respectively, and the closed-form secrecy outage probability expressions of secondary network under two relay selection modes is deduced. It is shown in simulations that the secrecy outage performance of secondary network is significantly affected by the number of primary receiver nodes and relays, the location of relays and the eavesdropping node, the ratio of energy harvesting, the efficiency of energy conversion, and the thresholds of channel capacity and secrecy capacity. The secrecy outage performance of the secondary network under the optimal relay selection scheme is obviously better than that of the suboptimal relay selection scheme. The secrecy outage probability of secondary network is reduced and tends to be saturated by increasing interference constraint or power beacon signals' power.
在认知协作中继网络(CCRN,cognitive cooperative relay network)中,次网络(SN,secondary network)信源节点既能通过选择的中继节点将数据转发给目的节点,从而提高SN传输的可靠性,又能通过与主网络(PN,primary network)共享频谱的方式,提高网络的频谱利用率,因此CCRN引起了研究者们的极大兴趣[1].由于无线通信的开放性,认知协作中继网络正面临着严峻的安全性问题[2].近几年来,以香农信息论为基础的CCRN物理层安全(PLS,physical layer security)性能分析逐渐成为了研究热点之一.
近来,对CCRN的PLS性能研究主要集中在分析网络的安全中断概率(SOP,secrecy outage probability)和窃听中断概率(IOP,intercept outage probability)这两方面. Nasr等[3]采用基于最小安全速率的中继选择方式来降低SN的SOP. Liu等[4]将友好人为干扰机引入CCRN,并推导了在四种中继选择方式下SN的SOP闭合式. Chakraborty等[5]推导了CCRN中SN源节点与目的节点和窃听节点间具有直接链路情况下SN的SOP闭合式. Jia等[6]研究了窃听链路信道状态信息(CSI,channel state information)无法实时获取以及具有人为噪声信号的CCRN,并求出了在2种机会中继选择方式下SN的SOP闭合式. Lei等[7]求导了CCRN在Nakagami-m信道下SN采用最优中继选择(ORS, optimal relay selection)、次优中继选择(SRS,suboptimal relay selection)和多中继合并(MRC,multiple relays combining)等3种中继选择方式的SOP闭合式. Ho-Van等[8]则分析了CCRN在SN源节点和窃听节点间具有直接链路情况下SN的近似和渐近IOP.
为了延长能量受限认知中继网络(CRN,cognitive relay network)的生存期,射频能量采集(RF-EH,radio frequency energy harvesting)技术被引入CRN,构建起了新的RF-EH-CRN.在RF-EH-CRN中,SN中继节点主要从PN发送节点[9]、SN源节点[10]和专用功率信标(PB,power beacon)[11]的射频信号中采集能量.目前,对RF-EH-CCRN的PLS性能研究方兴未艾. Li等[12]构建了一个覆盖式(overlay)RF-EH-CCRN,并得出了基于两个EH协议的最优中继选择方式下PN的精确和渐近SOP闭合式. Maji等[13]则研究了一个衬底式(underlay)RF-EH-CCRN,并在SN非完美CSI条件下对采用被动式中继选择方式的SOP进行了数值计算.现有的研究存在一定的局限性:①文献[12, 13]构建的RF-EH-CCRN中SN中继从PN节点或SN源节点的RF信号中采集能量.由于PN节点或SN源节点的发射功率远低于PB信号功率,导致SN中继从PN节点或SN源节点采集的能量远低于从PB信号中采集的[11]. ② Maji等[13]并未推导出SOP的闭合式.当前,对衬底式RF-EH-CCRN进行PLS性能研究的文献还很少.
在前人研究的基础上,笔者建立一个SN节点从PB信号采集能量的衬底式RF-EH-CCRN,推导出了SN采用ORS和SRS方式的SOP闭合式,并对2种不同中继选择方式下SN的安全中断性能进行了分析.笔者的主要贡献包括:①次网络中各中继节点分散分布,网络信道功率增益为独立非同分布;②推导出了更加科学的SOP闭合式.
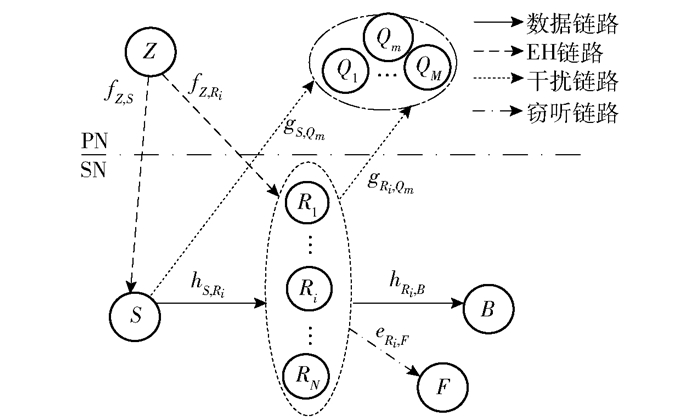
1 网络模型和安全容量 1.1 网络模型网络模型如图 1所示. M个PN接收节点Qm,m∈{1, 2, …, M}构成PN.源节点S、中继节点集合Φ={Ri|i=1, 2, …, N}和目的节点B则构成SN.单窃听节点F被随机设置在中继节点Ri附近,节点F会窃听Ri发送的信号,以图截获信息.假设PN对SN的干扰忽略不计,同时假设S与B和F之间的信道存在严重衰落,因此S与B和F之间不存在直接链路.网络中所有节点均使用单天线和半双工方式工作. SN采用underlay模式与PN共享频谱,即S采用主网络的授权频谱,通过选定的使用DF模式的中继节点Ri*向B转发信息.安装了RF-EH装置的Φ中所有中继和S同时从Z收集能量.网络中的所有链路均为独立Rayleigh块衰落信道,即信道系数在同一个时隙周期T内保持不变,在不同时隙间则独立变化. S到Ri以及Ri到B的数据链路信道系数分别表示为hS, Ri和hRi, B,Z到Ri和S的EH链路信道系数分别表示为fZ, Ri和fZ, S,S和Ri到Qm的干扰链路信道系数分别用gS, Qm和gRi, Qm表示,eRi, F则表示Ri到F的窃听链路信道系数.信道功率增益|hS, Ri|2、|hRi, B|2、|fZ, Ri|2、|fZ, S|2、|gS, Qm|2、|gRi, Qm|2和|eRi, F|2分别服从数学期望为1/λS, Ri、1/λRi, B、1/βRi、1/βS、1/ωS, Qm、1/ωRi, Qm和1/φRi, E的指数分布;例如,λS, Ri=dS, Riξ,其中dS, Ri为节点S到Ri的距离,ξ为路径损耗指数.为了简单起见,假设所有的Q紧绕同一个中心点设置[9].因此,S和Ri到Qm链路的信道增益分别是独立同分布的,即ωS, Qm= ωS和ωRi, Qm=ωRi.
|
图 1 网络系统模型 |
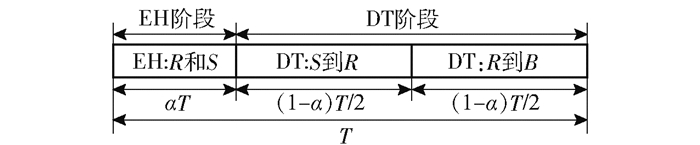
网络系统模型采用的传输协议时隙结构如图 2所示,协议分为EH和数据传输(DT,date transmission)2个阶段.时隙的前αT时段(α为EH比率,0 < α < 1)为EH阶段,节点q,q∈{S, Ri}收集到的能量为
|
图 2 传输协议的时隙结构 |
| $ {E_q} = \eta {P_{\rm{t}}}|{f_{Z,q}}{|^2}\alpha T $ | (1) |
其中:0 < η < 1为能量转换效率,Pt为发射功率.式(1)忽略了q收集的噪声能量.假设q的蓄电池容量无穷大,能将q收集到的能量全部存储,并且蓄电池存在漏电,在时隙结束时因其存储的能量被全部泄露,而不会用于下一时隙中.
在underlay模式下,SN节点发射功率严格受限,以保证Q接收到的SN节点信号功率不大于PN干扰约束PI,因此q的发射功率为
| $ {P_q} = {\rm{min}}\{ \rho {P_{\rm{t}}}{Z_q},{P_{\rm{I}}}/{Y_q}\} $ | (2) |
其中:
在DT阶段的前(1-α)T/2时段,Φ中所有中继均收到S发送的信号,Ri的瞬时接收端信噪比(SNR,signal-to-noise ratio)以及S到Ri的信道容量分别为
| $ {{\gamma _{S,{R_i}}} = {P_S}{X_{S,{R_i}}}/{\sigma ^2}} $ | (3) |
| $ {{C_{S,{R_i}}} = 0.5(1 - \alpha ) {\rm{lb}} (1 + {\gamma _{S,{R_i}}})} $ | (4) |
其中:XS, Ri=|hS, Ri|2,σ2为接收端加性复高斯白噪声方差.在前(1-α)T/2时段最后,Φ中所有中继对接收自S的数据进行译码.根据文献[7, 11],当CS, Ri大于数据传输速率阈值Rd时,Ri能成功译码.将成功译码的中继组成为集合D,由于Φ的基数为N,故集合D有2N种组合方式,即成功译码的结果集Ω={∅, D1, D2, …, Dn, …, D2N-1},其中∅表示空集,Dn则表示非空集合.若Ω=∅,则表明所有中继均未能成功解码S发送的信息,因此在DT阶段的后(1-α)T/2时段,所有中继将保持静默;若Ω=Dn,则在DT阶段的后(1-α)T/2时段,Ri(Ri∈Dn)将译码的S数据转发给B,B的瞬时接收端SNR为
| $ {\gamma _{{R_i},B}} = {P_{{R_i}}}{X_{{R_i},B}}/{\sigma ^2} $ | (5) |
其中XRi, B=|hRi, B|2.与此同时,F也接到Ri发送的信号,其瞬时接收端SNR为
| $ {\gamma _{{R_i},F}} = {P_{{R_i}}}{X_{{R_i},F}}/{\sigma ^2} $ | (6) |
其中XRi, F=|hRi, F|2. Ri到B和F链路信道容量分别为
| $ {{C_{{R_i},B}} = 0.5(1 - \alpha ){\rm{lb}}(1 + {\gamma _{{R_i},B}})} $ | (7) |
| $ {{C_{{R_i},F}} = 0.5(1 - \alpha ){\rm{lb}}(1 + {\gamma _{{R_i},F}})} $ | (8) |
为了降低系统的复杂度和减小SN的SOP,当Ω=Dn时,将采用以下2种中继选择方式.
1.2 ORS方式假设节点F采用主动窃听方式,此时Dn中的元素Ri可以实时获得其到B和F链路的瞬时CSI,此时采用ORS方式从Dn中选出中继Ri*ORS对B进行转发,其选择标准为
| $ {i^*} = {\rm{arg}}\mathop {{\rm{max}}}\limits_{{R_i} \in {D_n}} {[{C_{{R_i},B}} - {C_{{R_i},F}}]^ + } $ | (9) |
其中[x]+=max(x, 0).
| $ \begin{array}{l} C_S^{{\rm{ORS}}} = {[{C_{R_{{i^ * }}^{{\rm{ORS}}},B}} - {C_{R_{{i^ * }}^{{\rm{ORS}}},F}}]^ + } = \\ {\left[ {5(1 - \alpha ){\rm{lb}}\left( {\frac{{1 + {\gamma _{R_{{i^ * }}^{{\rm{ORS}}},B}}}}{{1 + {\gamma _{R_{{i^ * }}^{{\rm{ORS}}},F}}}}} \right)} \right]^ + } \end{array} $ | (10) |
其中:CRi*ORS, B和γRi*ORS, B分别表示Ri*ORS到B链路的信道容量以及B的接收端SNR,CRi*ORS, F和γRi*ORS, F则分别表示Ri*ORS到F链路的信道容量以及F的接收端SNR.
1.3 SRS方式假设节点F采用被动窃听方式,即F在窃听过程中始终保持静默,因此Dn中的元素Ri只能实时获得其到B链路的瞬时CSI,而无法实时获得其到E链路的瞬时CSI.此时,选择Dn中到B链路信道功率增益最大的中继Ri*SRS对B进行转发,其选择标准可以写为
| $ {i^*} = {\rm{arg}}\mathop {{\rm{max}}}\limits_{{R_i} \in {D_n}} {X_{{R_i},B}} $ | (11) |
采用SRS方式的SN安全容量为
| $ \begin{array}{l} C_S^{{\rm{SRS}}} = {[{C_{R_{{i^ * }}^{{\rm{SRS}}},B}} - {C_{R_{{i^ * }}^{{\rm{SRS}}},F}}]^ + } = \\ {\left[ {5(1 - \alpha ){\rm{lb}}\left( {\frac{{1 + {\gamma _{R_{{i^ * }}^{{\rm{SRS}}},B}}}}{{1 + {\gamma _{R_{{i^ * }}^{{\rm{SRS}}},F}}}}} \right)} \right]^ + } \end{array} $ | (12) |
其中:CRi*SRS, B和γRi*SRS, B分别表示Ri*SRS到B链路的信道容量以及B的接收端SNR,CRi*SRS, F和γRi*SRS, F则分别表示Ri*SRS到F链路的信道容量以及F的接收端SNR.
2 SN的SOP分析SOP是评价无线网络系统安全性能的重要指标之一,将瞬时安全容量低于预设目标速率阈值Rs的概率定义为SOP.根据全概率公式,SOP可以表示为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {P_{{\rm{ out }}}} = {\rm{Pr}}\{ {C_S} < {R_s}\} = \\ {\rm{Pr}} \{ {C_S} < {R_s},\varOmega = \varnothing \} + \sum\limits_{n = 1}^{{2^N} - 1} { {\rm{Pr}} } \{ {C_S} < {R_s},\varOmega = {D_n}\} \end{array} $ | (13) |
其中:Pr { ·}表示求概率运算.当Ω=∅时,Φ中所有中继均因未成功解码而无法向B转发数据,导致CS=0.因此,式(13)可以简化为
| $ {P_{{\rm{ out }}}} = {\rm{Pr}} \{ \varOmega = \varnothing \} + \sum\limits_{n = 1}^{{2^N} - 1} { {\rm{Pr}} } \{ {C_S} < {R_s},\varOmega = {D_n}\} $ | (14) |
为了简化SOP的计算,本节首先给出Yq和Uq=Pq/σ2,q∈{S, Ri}的累积分布函数(CDF,cumulative distribution function)和概率密度函数(PDF,probability density function).由于Yq是M个独立同分布的|gq, PRm|2,m∈{1, 2, …, M}最大值,且|gq, Qm|2均服从参数为1/ωq的指数分布,因此CDF和PDF分别为
| $ {F_{{Y_q}}}({y_q}) = {(1 - {{\rm{e}}^{ - {\omega _q}{y_q}}})^M} = \sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} {( - 1)^m}{{\rm{e}}^{ - m{\omega _q}{y_q}}} $ | (15) |
| $ {f_{{Y_q}}}({y_q}) = M{\omega _q}\sum\limits_{m = 0}^{M - 1} {\left( {\begin{array}{*{20}{c}} {M - 1}\\ m \end{array}} \right)} {( - 1)^m}{{\rm{e}}^{ - (m + 1){\omega _q}{y_q}}} $ | (16) |
Uq的CDF和PDF分别为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {F_{{U_q}}}({u_q}) = \\ 1 - {\rm{Pr }}\{ {Z_q} > {u_q}{\sigma ^2}/(\rho {P_{\rm{t}}})\} {\rm{Pr}} \{ {Y_q} < {P_{\rm{I}}}/({\sigma ^2}{u_q})\} = \\ 1 - \sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} {( - 1)^m}{{\rm{e}}^{ - {\beta _q}{u_q}{\sigma ^2}/(\rho {P_{\rm{t}}}) - m{\omega _q}{P_{\rm{I}}}/({\sigma ^2}{u_q})}} \end{array} $ | (17) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {f_{{U_q}}}({u_q}) = \frac{{\partial {F_{{U_q}}}({u_q})}}{{\partial {u_q}}} = \\ \sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} {( - 1)^m}\left( {\frac{{{\beta _q}{\sigma ^2}}}{{\rho {P_{\rm{t}}}}} - \frac{{m{\omega _q}{P_{\rm{I}}}}}{{{\sigma ^2}u_q^2}}} \right){{\rm{e}}^{ - \frac{{{\beta _q}{u_q}{\sigma ^2}}}{{\rho {P_{\rm{t}}}}} - \frac{{m{\omega _q}{P_{\rm{I}}}}}{{{\sigma ^2}{u_q}}}}} \end{array} $ | (18) |
本节将分别推导出采用ORS和SRS方式下SN的SOP闭式解,为后续的SN安全中断性能分析提供依据.
2.1 ORS方式下SN的SOP根据式(14),并使用全概率公式,可将采用ORS方式的SN精确安全中断概率改写为
| $ \begin{array}{l} P_{{\rm{ out }}}^{{\rm{ORS}}}({\gamma _d},{\gamma _s}) = \underbrace {{\rm{Pr}} \{ \varOmega = \varnothing \} }_{{J_1}({\gamma _d})} + \\ \underbrace {\sum\limits_{n = 1}^{{2^N} - 1} {{\rm{Pr}}} \{ C_S^{{\rm{ORS}}} < {R_s},\varOmega = {D_n}\} }_{{J_2}({\gamma _d},{\gamma _s})} \end{array} $ | (19) |
其中:J1(γd)可以计算为[5]
| $ \begin{array}{l} {J_1}({\gamma _d}) = \int_0^\infty {\prod\limits_{i = 1}^N {{\rm{ Pr }}} } \{ {\gamma _{S,{R_i}}} < {\gamma _d}|{U_S} = u\} {f_{{U_S}}}(u){\rm{d}}u = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 + \sum\limits_{k = 1}^{{2^N} - 1} {\sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} } {( - 1)^{m + \left| {{A_k}} \right|}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^\infty {\left( {\frac{{{\beta _S}{\sigma ^2}}}{{\rho {P_{\rm{t}}}}} - \frac{{m{\omega _S}{P_{\rm{I}}}}}{{{\sigma ^2}{u^2}}}} \right)} {{\rm{e}}^{ - \frac{{{\beta _{{S^{u\sigma }}^2}}}}{{\rho {P_{\rm{t}}}}} - \frac{{m{\omega _S}{P_{\rm{I}}}}}{{{\sigma ^2}u}} - \frac{{\sum\limits_{{R_i} \in {A_k}} {{\lambda _{S,{R_i}}}} {\gamma _d}}}{u}}}{\rm{d}}u \end{array} $ | (20) |
其中:γd=22Rd/(1-α)-1,Ak为Φ的子集,|Ak|表示集合Ak的基数.根据文献[15]中式(3.324.1)和式(3.471.9),J1(γd)可以写为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {J_1}({\gamma _d}) = 1 + \sum\limits_{k = 1}^{{2^N} - 1} {\sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} } {( - 1)^{m + |{A_k}|}} \times \\ [\begin{array}{*{20}{c}} 2&{\sqrt {{a_1}} ({\gamma _d}) - 2}&{\sqrt {{b_1}({\gamma _d})} } \end{array}]{{\rm{K}}_1}\left[ {\begin{array}{*{20}{l}} 2&{\sqrt {{a_1}} ({\gamma _d})} \end{array}} \right] \end{array} $ | (21) |
其中:
J2(γd, γs)则可以推导为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {J_2}({\gamma _d},{\gamma _s}) = \\ \sum\limits_{n = 1}^{{2^N} - 1} {\underbrace { {\rm{Pr}} \{ C_S^{{\rm{ORS}}} < {R_S}|\varOmega = {D_n}\} }_{{\vartheta _1}({\gamma _s})}} \underbrace {{\rm{Pr}} \{ \varOmega = {D_n}\} }_{{\vartheta _2}({\gamma _d})} \end{array} $ | (22) |
其中:ϑ1(γs)可以依据式(10)改写为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _1}({\gamma _s}) = {\rm{ Pr }}\left\{ {\mathop {{\rm{max}}}\limits_{{R_i} \in {D_n}} \left( {\frac{{1 + {\gamma _{{R_i},B}}}}{{1 + {\gamma _{{R_i},F}}}}} \right) < {\gamma _s}} \right\} = \\ \prod\limits_{{R_i} \in {D_n}} {\left\{ {1 - \sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{c}} M\\ m \end{array}} \right)} {{( - 1)}^m}\frac{{{\varphi _{{R_i},F}}}}{{{\varphi _{{R_i},F}} + {\lambda _{{R_i},B}}{\gamma _s}}} \times } \right.} \\ \left. {[\begin{array}{*{20}{c}} 2&{\sqrt {{a_2}} ({\gamma _s}) - 2}&{\sqrt {{b_2}({\gamma _s})} } \end{array}]{{\rm{K}}_1}[\begin{array}{*{20}{c}} 2&{\sqrt {{a_2}({\gamma _s})} } \end{array}]} \right\} \end{array} $ | (23) |
其中γs=22Rs/(1-α),
| $ \begin{array}{l} {a_2}({\gamma _s}) = \frac{{[m{\omega _{{R_i}}}{P_{\rm{I}}} + {\lambda _{{R_i},B}}({\gamma _s} - 1){\sigma ^2}]{\beta _{{R_i}}}}}{{\rho {P_{\rm{t}}}}}\\ {b_2}({\gamma _s}) = \frac{{{\beta _{{R_i}}}{m^2}\omega _{{R_i}}^2P_{\rm{I}}^2}}{{\rho {P_{\rm{t}}}[m{\omega _{{R_i}}}{P_{\rm I}} + {\lambda _{{R_i},B}}({\gamma _s} - 1){\sigma ^2}]}}\\ {\vartheta _2}({\gamma _d}) = \int_0^\infty {\prod\limits_{{R_i} \in {D_n}} { \rm Pr } } \{ {U_S}{X_{S,{R_i}}} > {\gamma _d}|{U_S} = u\} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \prod\limits_{{R_i} \in {{\bar D}_n}} { {\rm{Pr}} } \{ {U_S}{X_{S,{R_i}}} < {\gamma _d}|{U_S} = u\} {f_{{U_S}}}(u){\rm{d}}u = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} {( - 1)^m}2[\sqrt {{a_3}({\gamma _d})} - \sqrt {{b_3}({\gamma _d})} ] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {K_1}[2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{a_3}({\gamma _d})} ] + \\ \sum\limits_{k = 1}^{2\left| {{{\bar D}_n}} \right| - 1} {\sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} } {( - 1)^{|{C_k}| + m}}2[\sqrt {{a_4}({\gamma _d})} - \sqrt {{b_4}({\gamma _d})} ] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {K_1}[2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{a_4}({\gamma _d})} )] \end{array} $ | (24) |
其中:Dn是Dn的补集,Ck是Dn的子集,|Dn|和|Ck|分别表示Dn和Ck的基数,
| $ {a_3}({\gamma _d}) = \frac{{{\beta _S}\left( {m{\omega _S}{P_{\rm I}} + \sum\limits_{{R_i} \in {D_n}} {{\lambda _{S,{R_i}}}} {\gamma _d}{\sigma ^2}} \right)}}{{\rho {P_{\rm{t}}}}} $ |
| $ {b_3}({\gamma _d}) = \frac{{{\beta _s}{m^2}\omega _S^2P_{\rm{I}}^2}}{{\rho {P_{\rm{t}}}\left( {m{\omega _S}{P_{\rm{I}}} + \sum\limits_{{R_i} \in {D_n}} {{\lambda _{S,{R_i}}}} {\gamma _d}{\sigma ^2}} \right)}} $ |
| $ {a_4}({\gamma _d}) = \frac{{{\beta _s}\left( {m{\omega _s}{P_{\rm{I}}} + \sum\limits_{{R_i} \in {D_n}} {{\lambda _{s,{R_i}}}} {\gamma _d}{\sigma ^2} + \sum\limits_{{R_i} \in {C_k}} {{\lambda _{s,{R_i}}}} {\gamma _d}{\sigma ^2}} \right)}}{{\rho {P_{\rm{t}}}}} $ |
| $ {b_4}({\gamma _d}) = \frac{{{\beta _S}{m^2}\omega _S^2P_{\rm{I}}^2}}{{\rho {P_{\rm{t}}}\left( {m{\omega _S}{P_{\rm{I}}} + \sum\limits_{{R_i} \in {D_n}} {{\lambda _{S,{R_i}}}} {\gamma _d}{\sigma ^2} + \sum\limits_{{R_i} \in {C_k}} {{\lambda _{S,{R_i}}}} {\gamma _d}{\sigma ^2}} \right)}} $ |
将式(21)和式(22)代入式(19),可得采用ORS方式的SN安全中断概率PoutORS.
2.2 SRS方式下SN的SOP根据式(13),采用SRS方式的SN精确SOP可以表示为
| $ \begin{array}{l} P_{{\rm{ out }}}^{{\rm{SRS}}}({\gamma _d},{\gamma _s}) = \underbrace {{\rm{ Pr }}\{ \varOmega = \varnothing \} }_{{J_1}({\gamma _d})} + \\ \underbrace {\sum\limits_{n = 1}^{{2^N} - 1} { {\rm{Pr }}} \{ C_S^{{\rm{SRS}}} < {R_s},\varOmega = {D_n}\} }_{{J_3}({\gamma _d},{\gamma _s})} \end{array} $ | (25) |
其中:J3(γd, γs)可以计算为
| $ {J_3}({\gamma _d},{\gamma _s}) = \sum\limits_{n = 1}^{{2^N} - 1} {\underbrace { {\rm{Pr}} \{ C_S^{{\rm{SRS}}} < {R_s}|\varOmega = {D_n}\} }_{{\vartheta _3}({\gamma _s})}} \underbrace {{\rm{Pr}} \{ \varOmega = {D_n}\} }_{{\vartheta _2}({\gamma _d})} $ | (26) |
其中:ϑ3(γs)可以依据式(12)表示为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _3}({\gamma _s}) = \\ \sum\limits_{{R_i} \in {D_n}} { {\rm{Pr}} } \{ {X_{{R_i},B}} > \mathop {{\rm{max}}}\limits_{{R_l} \in \{ {D_n} - {R_i}\} } {X_{{R_l},B}}\} {\rm{Pr }}\left\{ {\frac{{1 + {\gamma _{{R_i},B}}}}{{1 + {\gamma _{{R_i},F}}}} < {\gamma _s}} \right\} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{R_i} \in {D_n}} {\left\{ {1 - \sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} \frac{{{{( - 1)}^m}{\varphi _{{R_i},F}}}}{{{\varphi _{{R_i},F}} + {\gamma _s}{\lambda _{{R_i},B}}}} \times } \right.} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2[\sqrt {{a_2}({\gamma _s})} - \sqrt {{b_2}({\gamma _s})} ] \times \\ {{\rm{K}}_1}[2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{a_2}({\gamma _s})} ] + \sum\limits_{k = 1}^{{2^{|{D_n}| - 1}} - 1} {\frac{{{{( - 1)}^{\left| {{G_k}} \right|}}{\lambda _{{R_i},B}}}}{{{\lambda _{{R_i},B}} + \sum\limits_{{R_l} \in {G_k}} {{\lambda _{{R_l},B}}} }}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [1 - \sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} {( - 1)^m}2[\sqrt {{a_5}({\gamma _s})} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{b_5}({\gamma _s})} ]{{\rm{K}}_1}[2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{a_5}({\gamma _s})} ]] + \\ \sum\limits_{k = 1}^{{2^{\left| {{D_n}} \right| - 1}} - 1} {\sum\limits_{m = 0}^M {\left( {\begin{array}{*{20}{l}} M\\ m \end{array}} \right)} } \frac{{{{( - 1)}^{|{G_k}| + m}}{\gamma _s}{\lambda _{{R_i},B}}}}{{{\varphi _{{R_i},F}} + {\gamma _s}{\lambda _{{R_i},B}} + {\gamma _s}\sum\limits_{{R_l} \in {G_k}} {{\lambda _{{R_l},B}}} }} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2[\sqrt {{a_5}({\gamma _s})} - \sqrt {{b_5}({\gamma _s})} ]{{\rm{K}}_1}[2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{a_5}({\gamma _s})} ]\} \end{array} $ | (27) |
其中:{Dn-Ri}表示Dn去除元素Ri后的中继集合,Gk为{Dn-Ri}的子集,|Gk|为Gk的基数,
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_5}({\gamma _s}) = \\ \frac{{{\beta _{{R_i}}}\left[ {m{\omega _{{R_i}}}{P_{\rm{I}}} + \left( {{\lambda _{{R_i},B}} + \sum\limits_{{R_l} \in {G_k}} {{\lambda _{{R_l},B}}} } \right)({\gamma _s} - 1){\sigma ^2}} \right]}}{{\rho {P_{\rm{t}}}}} \end{array} $ |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_5}({\gamma _s}) = \\ \frac{{{\beta _{{R_i}}}{m^2}\omega _{{R_i}}^2P_{\rm{I}}^2}}{{\rho {P_{\rm{t}}}\left[ {m{\omega _{{R_i}}}{P_{\rm{I}}} + \left( {{\lambda _{{R_i},B}} + \sum\limits_{{R_l} \in {G_k}} {{\lambda _{{R_l},B}}} } \right)({\gamma _s} - 1){\sigma ^2}} \right]}} \end{array} $ |
将式(24)和式(27)代入式(26)可得J3(γd, γs);最终将式(21)和式(26)代入式(25)可得SRS方式下的SN安全中断概率PoutSRS.
3 仿真结果与分析本节给出SOP的仿真和数值计算结果与分析. Monte Carlo仿真次数设置为105.除非另有说明,网络模型中的各参数设置如表 1所示. Pt和PI均被σ2归一化.
|
|
表 1 网络仿真参数设置 |
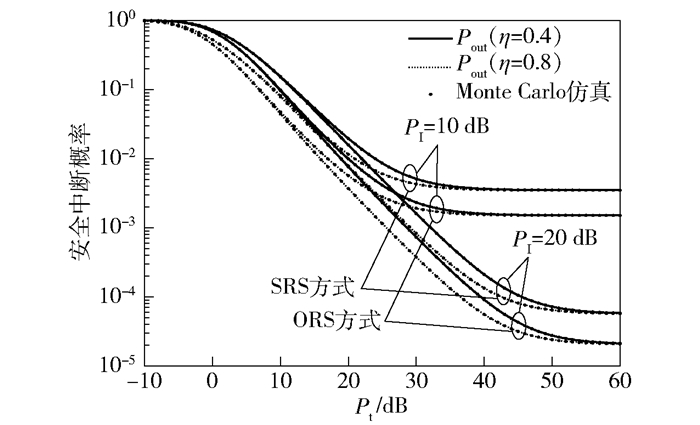
从图 3~7可以看出:① Monte Carlo仿真曲线与数值计算曲线高度吻合,证明了理论推导的正确性. ②在相同参数设置情况下,PoutORS低于PoutSRS.如Pt=15 dB,PI=10 dB,M=N=3时,PoutORS和PoutSRS分别为1.51%和2.89%,ORS方式下的SN安全中断性能较SRS方式下的提升了91.39%.
|
图 3 不同η和PI下SOP与Pt之间的关系 |
|
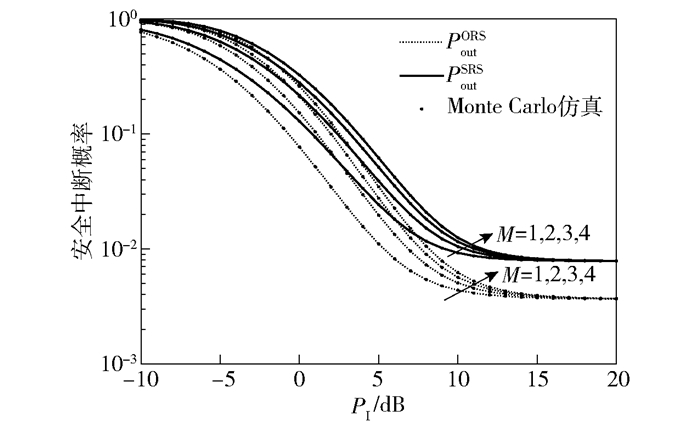
图 4 图 4不同M下SOP与PI之间的关系 |
|
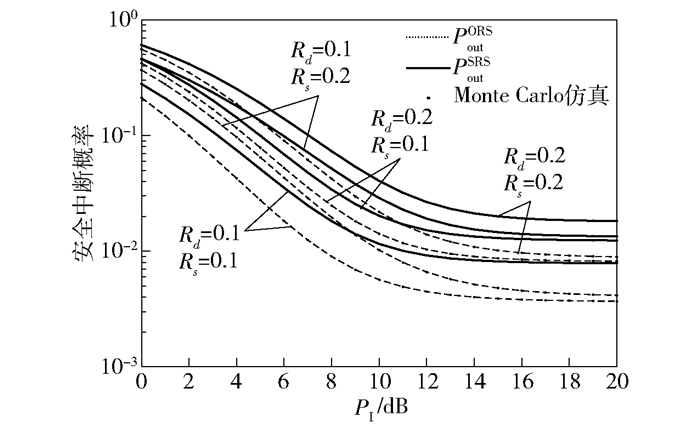
图 5 不同Rd和Rs下SOP与PI之间的关系 |
|
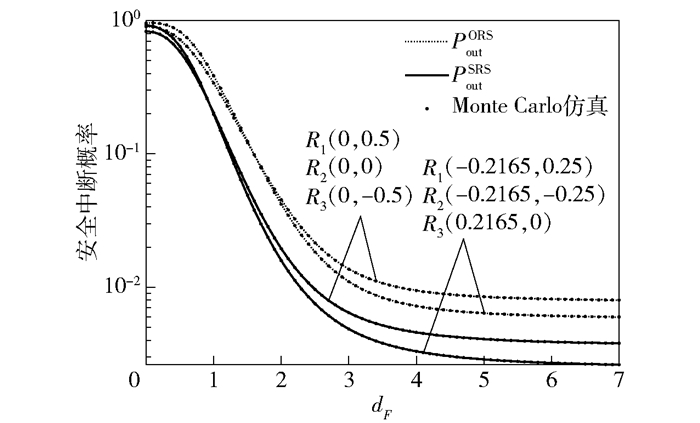
图 6 不同中继位置下SOP与dF之间的关系 |
|
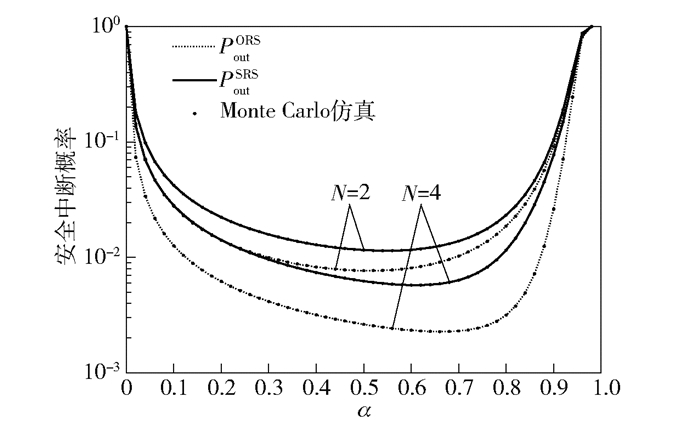
图 7 不同N下SOP与α之间的关系 |
图 3所示为η=0.4, 0.8,PI=10, 20 dB,N=3时,SOP与Q发射功率Pt之间的关系.可以看出:①当PI和η给定时,PoutORS和PoutSRS均随Pt的增大而单调下降,并趋于饱和.随着Pt的增大,SN节点因采集到的能量增加而导致其发射功率变大,SOP降低,但SN节点的发射功率因受PI限制而不会无限制增加,最终其发射功率和SN的SOP均将趋于饱和;②当PI和Pt给定时,η的增大有助于降低SOP;③当η和Pt给定时,PI的提高将使SOP降低.
图 4和图 5展示了M=2, 3, 4,N=3,Pt=20 dB,以及Rd和Rs取不同值时,SOP与PI之间的关系. 可以发现:①与图 3类似,当Pt、M、Rd和Rs给定时,PoutORS和PoutSRS也随PI的增大而单调下降,并趋于饱和.由于CCRN是干扰受限网络,Pt给定,致使SN节点采集的能量一定,随着PI的提高,SN节点能将更多能量用于提高发射功率直至耗尽所有存储能量,此时SN节点发射功率Pq、PoutORS和PoutSRS也将饱和. ②当Pt、PI、Rd和Rs给定时,随着M的增大,Yq获得更大值的概率变大,导致Pq减小,从而使得PoutORS和PoutSRS增大. ③当Pt、PI、M给定时,PoutORS和PoutSRS随Rd和Rs的增大而提高,且ORS方式下Rd对SOP的影响大于Rs对SOP的影响,在SRS方式下则相反.
图 6体现了中继R1、R2和R3处于2种不同位置设置方式时,SOP与dF之间的关系,其中:Pt=20 dB,PI=15 dB,dF表示F沿X正半轴移动时其与原点之间的距离.可以看出:①当中继位置确定时,随着dF的增大,F逐步远离EH-CCRN,其接收端SNR将逐步降低,并趋近于0,导致PoutORS和PoutSRS随之减小,并趋于饱和. ②当dF给定时,不同的中继位置设置方式对PoutORS和PoutSRS会产生较大影响.
图 7所示为N=2, 3时,PoutORS和PoutSRS与α之间的关系,其中:Pt=20 dB,PI=15 dB.可以发现:①当N给定时,PoutORS和PoutSRS随α的增大逐步从1减小到最小值,再增大到1. ②当N取不同值时,PoutORS和PoutSRS最小值所对应的α各不相同.如N=2,α为0.52和0.54时,PoutORS和PoutSRS可分别取得最小值0.77%和1.14%;N=3,则α为0.66和0.6时,PoutORS和PoutSRS可分别取得最小值0.23%和0.58%. ③随着N值增大,PoutORS和PoutSRS减小.
4 结束语构建了一个新的单向两跳EH-CCRN.在时隙的EH阶段,S和所有的中继节点均从PB的射频信号中采集能量.在随后的DT阶段,考虑单窃听节点采用主动和被动窃听方式,分别采用ORS和SRS方式选择中继,推导出了2种中继选择方式下SN的精确SOP闭合式.理论和仿真结果表明,ORS方式下SN安全中断性能较SRS方式下提升明显;SN的SOP都会随着Pt或PI的增大而单调下降,最终出现饱和现象;随着M的增大,SN的SOP也增大;F逐步远离EH-CCRN,SN的SOP随之减小,并趋于饱和;实时调整α和N值有助于提高SN中断性能.
| [1] |
Tavana M, Rahmati A, Shah-Mansouri V, et al. Cooperative sensing with joint energy and correlation detection in cognitive radio networks[J]. IEEE Communications Letters, 2017, 21(1): 132-135. DOI:10.1109/LCOMM.2016.2613858 |
| [2] |
Liu Yiliang, Chen H H, Wang Lingmin. Physical layer security for next generation wireless networks:theories, technologies, and challenges[J]. IEEE Communications Surveys and Tutorials, 2017, 19(1): 347-376. DOI:10.1109/COMST.2016.2598968 |
| [3] |
Nasr O, El-Rabaie S, Sakran H, et al. Proposed relay selection scheme for physical layer security in cognitive radio networks[J]. IET Communications, 2012, 6(16): 2676-2687. DOI:10.1049/iet-com.2011.0638 |
| [4] |
Liu Y W, Wang L F, Duy T T, et al. Relay selection for security enhancement in cognitive networks[J]. IEEE Wireless Communications Letters, 2015, 4(1): 46-49. DOI:10.1109/LWC.2014.2365808 |
| [5] |
Chakraborty P, Prakriya S. Secrecy outage performance of a cooperative cognitive relay network[J]. IEEE Communications Letters, 2017, 21(2): 326-329. DOI:10.1109/LCOMM.2016.2564380 |
| [6] |
Jia Shaobo, Zhang Jiayan, Zhao Honglin, et al. Relay selection for improved security in cognitive relay networks with jamming[J]. IEEE Wireless Communications Letters, 2017, 6(5): 662-665. DOI:10.1109/LWC.2017.2728528 |
| [7] |
Lei H J, Zhang H, Ansari I S, et al. On secrecy outage of relay selection in underlay cognitive radio networks over Nakagami-m fading channels[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(4): 614-627. DOI:10.1109/TCCN.2017.2758372 |
| [8] |
Ho-Van K, Do-Dac T. Analysis of security performance of relay selection in underlay cognitive networks[J]. IET Communications, 2018, 12(1): 102-108. DOI:10.1049/iet-com.2017.0445 |
| [9] |
Liu Y W, Mousavifar S, Deng Y S, et al. Wireless energy harvesting in a Cognitive Relay Network[J]. IEEE Transactions on Wireless Communications, 2016, 15(4): 2498-2508. DOI:10.1109/TWC.2015.2504520 |
| [10] |
Nguyen D K, Jayakody D N, Chatzinotas S, et al. Wireless energy harvesting assisted two-way cognitive relay networks:protocol design and performance analysis[J]. IEEE Access, 2016, 5: 21447-21460. |
| [11] |
Xu Chi, Zheng Meng, Liang Wei, et al. Outage performance of underlay multihop cognitive relay networks with energy harvesting[J]. IEEE Communications Letters, 2016, 20(6): 1148-1151. DOI:10.1109/LCOMM.2016.2547985 |
| [12] |
Li Mu, Yin Hao, Huang Y Z, et al. Physical layer security in overlay cognitive radio networks with energy harvesting[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 11274-11279. DOI:10.1109/TVT.2018.2868902 |
| [13] |
Maji P, Prasad B, Roy S D, et al. Secrecy outage of a cognitive radio network with selection of energy harvesting relay and imperfect CSI[J]. Wireless Personal Communications, 2018, 100(2): 571-586. DOI:10.1007/s11277-017-5221-0 |
| [14] |
Zou Yulong, Wang Xianbin, Shen Weiming, et al. Security versus reliability analysis of opportunistic relaying[J]. IEEE Transactions on Vehicular Technology, 2014, 63(6): 2653-2661. DOI:10.1109/TVT.2013.2292903 |
| [15] |
Gradshteyn I S, Rythik I M, Jeffrey A, et al. Table of integrals, series, and products[M]. New York: Academic Press, 2007.
|


